有限元-点插值耦合法大地电磁二维正演模拟

李俊杰,严家斌

(1.浙江省水利水电勘测设计院,浙江杭州310002;2.中南大学地球科学与信息物理学院,有色资源与地质灾害探查湖南省重点实验室,湖南长沙410083)

有限元-点插值耦合法大地电磁二维正演模拟

李俊杰1,严家斌2

(1.浙江省水利水电勘测设计院,浙江杭州310002;2.中南大学地球科学与信息物理学院,有色资源与地质灾害探查湖南省重点实验室,湖南长沙410083)

点插值法(PIM)作为一种典型的全域弱式无网格法,该方法在地质建模时将物性加载到只与坐标有关的高斯积分点上,因此处理复杂模型时较常规网格方法便利,但缺点是计算效率低。将有限元法(FEM)与PIM耦合,形成FE-PIM,用于大地电磁二维正演模拟。利用Galerkin法代入插值法构造的形函数并结合高斯积分公式推导了大地电磁二维无网格化总体矩阵表达式,简述了背景网格积分与边界条件的加载技术,理论模型的数值计算验证了FE-PIM算法的正确性、高效性及其在处理复杂模型上的便利性。

点插值法;全域弱式无网格法;大地电磁;有限元-点插值法

大地电磁二维正演多采用有限差分法(finite deference method,FDM)[1-2]、有限元法(finite element method,FEM)[3-6]等网格方法。对于地质体相对规则、地形简单的模型,FDM利用较小的网格就能获得较高的计算精度,效率高;而对于复杂的地质体,就需要精细网格才能完成高精度的模拟。FEM适用于复杂边界与复杂电性结构模型的计算,但高维问题中非结构化三角单元生成程序实现困难。无单元Galerkin法(element-free Galerkin method,EFGM)[7]是一种基于节点的全域弱式无网格方法,其形函数构造不依赖预定义的网格单元,选择离散的节点便可求Helmholtz方程的解。相对于低阶(low-order)有限元分析,EFGM只需少量的节点就可获得光滑的解,且场分量的导数同样光滑连续,对于大地电磁辅助分量的求解非常有利,可以获得与主分量(水平电场或磁场)相同的计算精度,对于节点的参数化处理也较单元分析容易。EFGM能处理网格方法难以处理的问题[8-10],有广阔的应用前景。李俊杰等[11]综述了无网格法进展并推导了大地电磁二维问题的无网格化系统矩阵表达式;贾晓峰等[12-13]将EFGM用于叠前地震模拟,并讨论了几种吸收边界方法在地震模拟中与EFGM的结合,研究结果表明，EFGM精度较FDM精度高，且具有较好的稳定性;王月英[14]分析了基函数阶次对EFGM用于地震波正演计算精度的影响;冯德山等[15]、戴前伟等[16]将EFGM用于雷达波场的二维正演模拟,详细推导了探地雷达无单元法波动方程,并提出了适用于EFGM雷达正演模拟的透射吸收边界、Sarma吸收边界的改进方法。严家斌等[17]将EFGM成功应用于大地电磁二维正演模拟,并分析了支持域无量纲尺寸与高斯点数量对无网格法正演计算精度与效率的影响。无网格点插值法(point interpolation method,PIM)[18]是另一种简单高效的全域弱式无网格法,与EFGM的区别主要在于形函数采用过点插值的方法进行构造,边界条件加载便利。李俊杰等[19]将PIM用于复杂模型的MT二维正演模拟,凸显了PIM较常规网格方法在地质建模上的优越性。

我们将PIM与高效的FEM相耦合,形成有限元-点插值法(finite element-point interpolation method,FE-PIM),从大地电磁场的二维正演理论出发,采用Galerkin法推导了FE-PIM系统矩阵表达式,数值计算结果验证了FE-PIM的有效性及其在计算复杂模型时高效、便利的特性。

1 大地电磁二维变分问题

研究地下二维电性结构,取y轴垂直向上,z轴为走向,x轴向右且与y轴、z轴垂直,求解域Ω为矩形,4个顶点依次以A,B,C,D顺时针编号,Γ1为地质体边界。大地电磁二维正演满足(1)式所示的变分问题[20]:

(1a)

uAB=1

(1b)

δF(u)=0

(1c)

TE模式为:

u=Ez

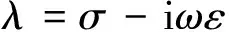
(2)

TM模式为:

u=Hz

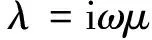
(3)

式中:ω为角频率;μ为磁导率;σ为电导率;ε为介电常数;Ez,Hz分别为电场及磁场平行于异常体走向的水平分量。

2 大地电磁二维变分问题的无网格解法

PIM以积分点支持域内的场节点利用多项式基插值构造形函数,背景网格用于计算总体矩阵表达式中包含的求解域及求解域边界的积分项。图1 为PIM支持域、高斯点、背景网格与场节点示意图。由于网格积分多采用高斯积分法,故积分点也称高斯点。

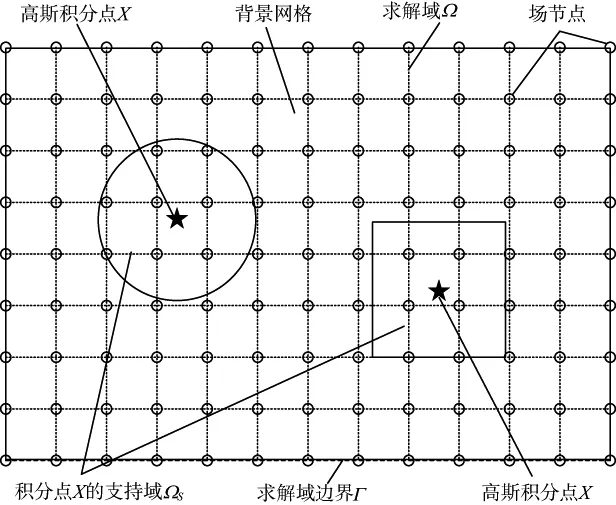
图1 全域弱式无网格法支持域、高斯点、背景网格与场节点图示

2.1 支持域

如图1所示,支持域形状常为矩形或圆形,对于任一高斯点XQ,支持域尺寸d可表示为:

(4)

式中:α为支持域无量纲尺寸,其大小影响无网格法的计算精度[17];dc为支持域内高斯点XQ的平均结点间距,有:

(5)

式中:A为支持域面积;n为包含在A中的节点总数。本文采用矩形支持域,x,y方向的支持域尺寸为：

(6)

式中:dcx与dcy分别为x,y方向的节点间距;αx与αy为对应的无量纲尺寸。为便于程序设计,一般令αx=αy=α,本文取α=1。

2.2 FE-PIM离散系统方程的构造

PIM计算效率低但处理复杂模型便利[19],FEM求解高效,由于PIM与FEM系统矩阵采用相同的方法构成,故PIM与FEM具有很好的耦合条件。

如图2所示,FE-PIM的基本原理是将求解域Ω划分为实线表示的FEM区域Ω1及虚线表示的PIM背景单元区域Ω2,异常体置于Ω2,无穷远边界单元设为Ω1。将变分符号δ代入(1)式并将FEM区域单元离散化,有:

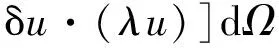
(7)

式中:e表示FEM的子单元;CD为求解域底边界;Γe为边界单元。

图2 FE-PIM计算模型二有限单元与背景网格分布图示

将FEM区域的积分项即δF1(u)离散,有:

(8)

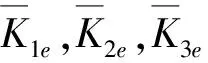
(9)

式中:U为全部节点的场值向量;KFEM为FEM区域计算的总体系统矩阵。求得δF1(u)的离散表达式后,将δF2(u)离散,将u表示为PIM形函数向量与场节点向量之积的形式,有

(10)

式中:Φ为用PIM构造的形函数矩阵[18-19];n为支持域内的节点数;u为支持域内n个节点的场向量值。对(10)式进行变分运算,有:

(11)

将(10)式与(11)式代入(1)式的第1项并引入总体编号体系,总体矩阵最终变为:

(12)

式中:M1与Mn表示PIM区域第一个节点与最后一个节点的编号;KPIM为背景单元域PIM计算的总体系统矩阵。KPIM表达式中包含对求解域Ω2的积分,积分利用高斯积分法求解,有:

(13)

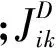
(14)

由于δUT的任意性,(14)式成立的条件变为:

(15)

(15)式即为用FE-PIM构造的系统矩阵,由于FEM与PIM构造的总体矩阵KFEM及KPIM均具有带状、稀疏、对称的性质,故K也具备该特性。

线性方程组KU=0的求解需加载(1)式所示的边界条件,PIM与FEM边界条件均可直接加载,计算时先找出边界节点在总体刚度矩阵中对应的KII,KII对应的行与列设置为0,其值设置为1,最后将方程右端项对应的值PI设置为边界上的预设场值即可。PIM边界条件可精确加载,该特性是PIM较EFGM最大的优势。

3 正演计算

3.1 算法验证

PIM与FEM在一维介质大地电磁(MT)正演中具有较高的精度[19],FE-PIM为两者的耦合,先通过图3所示的COMMEMI 2D-0模型[21]来验证文中算法的正确性。此模型异常体顶部与地表重合,纵向规模50km,横向规模20km,电阻率为1Ω·m,其左、右两侧电阻率分别为10Ω·m和2Ω·m,深度大于50km区域为超导层,电阻率为0,求解域TE模式取120km×110 km,TM模式取120km×70km,场节点横纵向等间距分布,节点间距为1km。

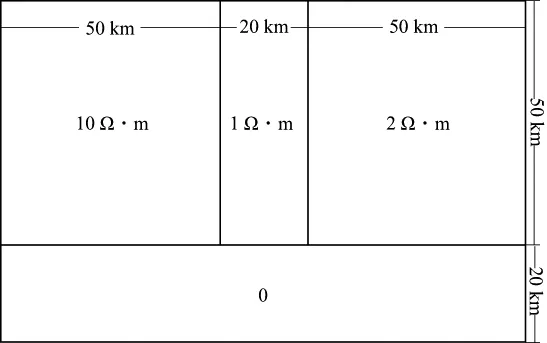
图3 COMMEMI 2D-0模型

表1列出了PIM与FEM计算COMMEMI 2D-0模型的视电阻率结果。从表1可以看出,两种方法计算结果与COMMEMI解析解基本吻合,验证了数值算法的有效性。此外,表1中FEM计算结果也与文献[22]一致。

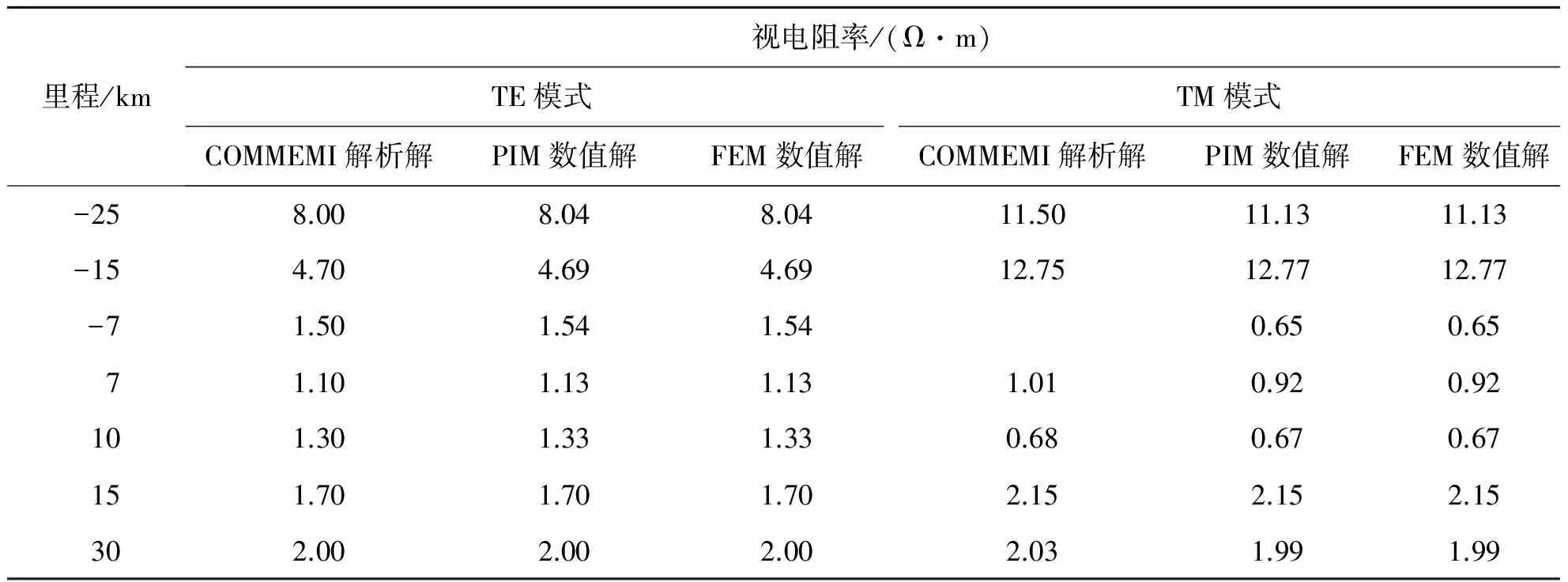
表1 COMMEMI 2D-0模型数值方法视电阻率计算结果

3.2 有效性及优势

为进一步验证FE-PIM有效性及其优势,设计了如图4所示的二维地质模型:模型二异常体为截面方形二度体,异常体边长400m,埋深800m;模型三为水平椭圆,长半轴300m,短半轴200m,埋深800m;模型四为等腰直角三角形地垒,斜边长800m;模型五为出露于地表的条带状低阻体,异常体截面呈平行四边形,下底长400m,上、下底间距800m,异常体右边界与地面的夹角呈45°。

模型背景电阻率1000Ω·m,异常体电阻率100Ω·m。场节点等间距分布于求解域,TE模式3321(41×81)个场节点,TM模式1681(41×41)个场节点,横、纵向节点间距均为200m,FEM与FE-PIM采用相同的节点分布。

图5显示了频率为100Hz时PIM与FEM模型二视电阻率计算结果。从图5可以看出,求解域两侧边界的视电阻率值约为1000Ω·m,低阻异常在里程0附近最显著,TE模式视电阻率值约780Ω·m,TM模式约920Ω·m。两种模式下FE-PIM,PIM与FEM的计算结果基本一致,验证了FE-PIM二维算法的正确性。

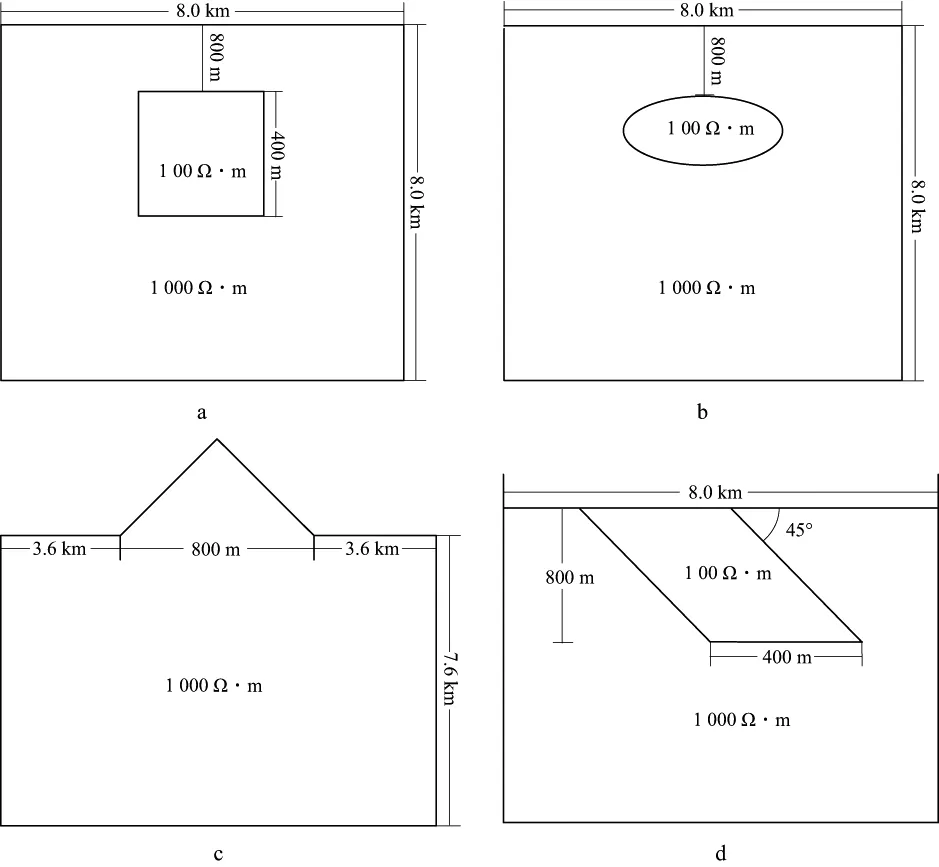
图4 二维地质模型

图5 频率为100Hz时模型二视电阻率计算结果

图6为不同模型的FE-PIM视电阻率计算结果。从图6a和图6b可以看出,TE模式低阻异常中心与模型中心一致,能明显地反映出椭圆低阻体的存在,但异常规模比实际低阻体大,视电阻率为740～1080Ω·m。TM模式低阻异常呈直立状并无限向下延伸,异常的水平宽度反映了实际低阻体水平方向的尺寸,视电阻率为800～1060Ω·m。从图6c可以看出,模型四山脊位置在视电阻率断面图上显示为高阻极大值区域,两侧的山谷区则呈现低阻极小值,且频率越高此特性越明显,视电阻率变化范围为900～1950Ω·m,此现象表明地形对大地电磁测深法影响规律与直流电阻率法存在差异。断面图高阻区的横向规模约800m,与山脊横向规模相当,验证了FE-PIM的有效性。从图6d 可以看出,模型五的视电阻率断面图左右非对称,低阻区域呈“上窄下宽”条带状倾斜分布,倾向与地质体相同,视电阻率为100～1100Ω·m,较好地反映出了异常体的物性及空间赋存状态。

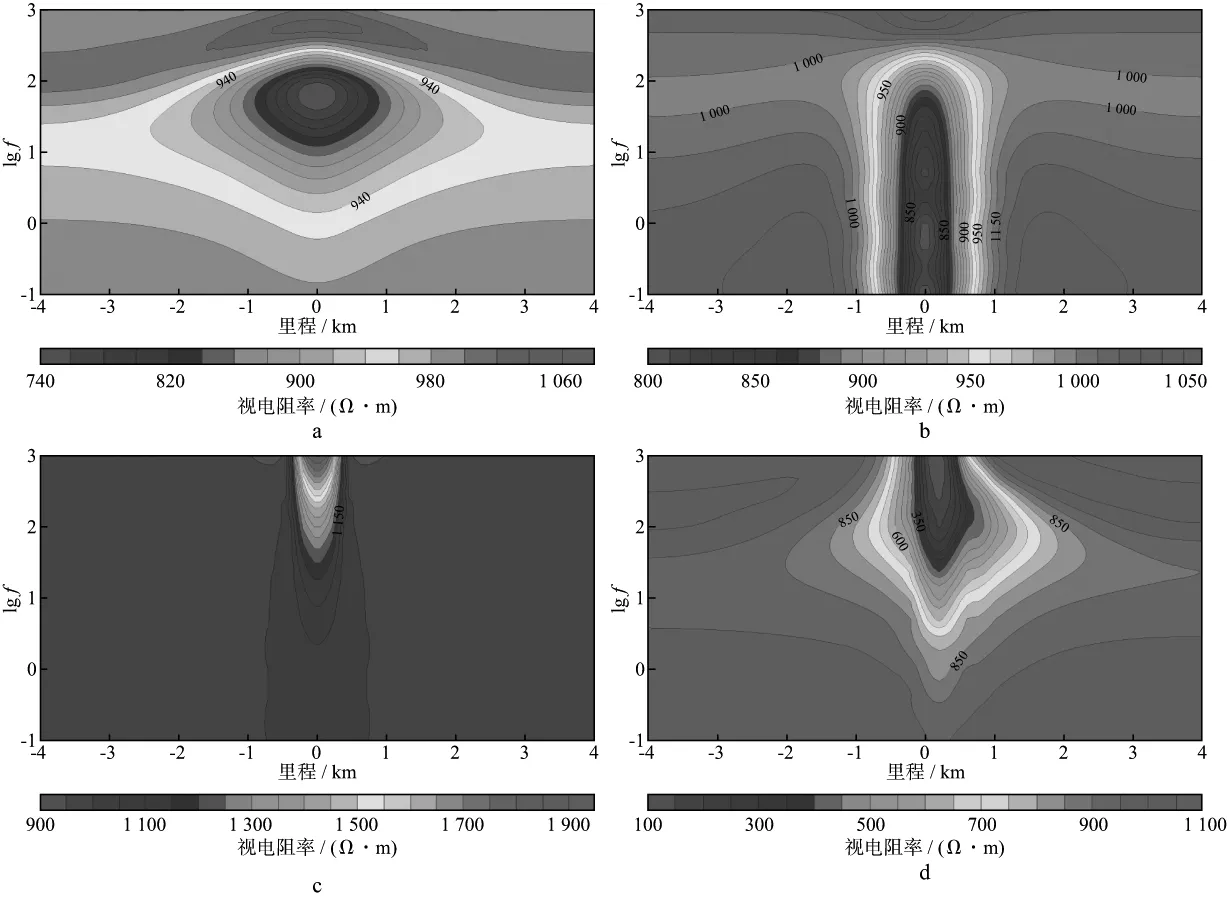
图6 不同模型的视电阻率FE-PIM计算结果

FE-PIM延续PIM地质建模便利特点的同时也兼顾了计算效率,表2列出了17个频点PIM,FE-PIM与FEM的计算耗时。从表2可以看出,PIM耗时约为FEM耗时的8～9倍,FE-PIM耗时相对PIM耗时呈著降低,无网格区域(10×4)的FE-PIM与PIM相比，TE模式下效率约提高87%,TM模式下效率约提高83%,随着FEM区域的增大,FE-PIM耗时逐渐接近FEM耗时。

表2 模型二不同数值方法计算耗时

4 结束语

1) 将FE-PIM应用于大地电磁二维正演模拟,通过把求解区域划分为有限元区域及背景单元区域,利用Galerkin法和高斯积分公式导出了大地电磁二维FE-PIM耦合的系统方程离散表达式,介绍了边界条件直接加载的技巧,COMMEMI 2D-0 模型的数值计算验证了文中PIM与FEM算法的正确性。

2) 采用节点规则分布的FE-PIM计算了截面为方形、椭圆、平行四边形及三角地垒二维模型的大地电磁场响应,视电阻率断面图较好地反映了地质体产生的电磁异常响应及空间赋存状态,验证了耦合算法的正确性,凸显了FE-PIM处理复杂地质模型的优越性。

3) 比较分析了PIM,FE-PIM及FEM的计算效率,PIM计算耗时明显高于FEM计算耗时;FE-PIM计算耗时受异常体区域的影响较大,当异常体区域较小时,FE-PIM计算耗时远小于PIM计算耗时而略高于FEM计算耗时,但FE-PIM综合了FEM计算高效及PIM处理复杂模型便利的优点,是一种优越的数值方法。

[1] 胡祥云,霍光谱,高锐,等.大地电磁各向异性二维模拟及实例分析[J].地球物理学报,2013,56(12):4268-4277 Hu X Y,Huo G P,Gao R,et al.The magnetotelluric anisotropic two-dimensional simulation and case analysis[J].Chinese Journal of Geophysics,2013,56(12):4268-4277

[2] 董浩,魏文博,叶高峰,等.基于有限差分正演的带地形三维大地电磁反演方法[J].地球物理学报,2014,57(3):939-952 Dong H,Wei W B,Ye G F,et al.Study of three-dimensional magnetotelluric inversion including surface topography based on finite-difference method[J].Chinese Journal of Geophysics,2014,57(3):939-952

[3] Key K,Weiss C.Adaptive finite-element modeling using unstructured grids:the 2D magnetotelluric example[J].Geophysics,2006,71(6):291-299

[4] 刘长生,汤井田,任政勇,等.基于非结构化网格的三维大地电磁自适应矢量有限元模拟[J].中南大学学报(自然科学版),2010,41(5):1855-1859 Liu C S,Tang J T,Ren Z Y,et al.Three-dimension magnetotellurics modeling by adaptive edge finite-element using unstructured meshes[J].Journal of Central South University(Science and Technology),2010,41(5):1855-1859

[5] Ren Z Y,Tang J T.3D direct current resistivity modeling with unstructured mesh by adaptive finite-element method[J].Geophysics,2010,75(1):7-17

[6] 柳建新,孙丽影,童孝忠,等.基于自适应有限元的起伏地形MT二维正演模拟[J].地球物理学进展,2012,27(5):2016-2023 Liu J X,Sun L Y,Tong X Z,et al.Undulating terrain 2D MT forward modelling with adaptive finite element[J].Progress in Geophysics,2012,27(5):2016-2023

[7] Belytschko T,Lu Y Y,Gu L.Element-free Galerkin methods[J].International Journal for Numerical Methods in Engineering,1994,37(2):229-256

[8] Belytschko T,Lu Y Y,Gu L.Fracture and crack growth by element-free Galerkin methods[J].Modelling and Simulation in Materials Science and Engineering,1994,2(3):519-534

[9] Li D M,Bai F N,Cheng Y M,et al.A novel complex variable element-free Galerkin method for two-dimensional large deformation problems[J].Computer Methods in Applied Mechanics and Engineering,2012,233-236(1):1-10

[10] Liu L C,Dong X H,Li C X.Adaptive finite element-element-free Galerkin coupling method for bulk metal forming processes[J].Journal of Zhejiang University-Science A,2009,10(3):353-360

[11] 李俊杰,严家斌.无网格法进展及其在地球物理学中的应用[J].地球物理学进展,2014,29(1):452-461 Li J J,Yan J B.Developments of meshless method and applications in geophysics[J].Progress in Geophysics,2014,29(1):452-461

[12] 贾晓峰,胡天跃,王润秋.复杂介质中地震波模拟的无单元法[J].石油地球物理勘探,2006,41(1):43-48 Jia X F,Hu T Y,Wang R Q.A mesh-free algorithm of seismic wave simulation in complex medium[J].Oil Geophysical Prospecting,2006,41(1):43-48

[13] 贾晓峰,胡天跃,王润秋.无单元法用于地震波波动方程模拟与成像[J].地球物理学进展,2006,21(1):11-17 Jia X F,Hu T Y,Wang R Q.Wave equation modeling and imaging by using element-free method[J].Progress in Geophysics,2006,21(1):11-17

[14] 王月英.地震波正演模拟中无单元Galerkin法初探[J].地球物理学进展,2007,22(5):1539-1544 Wang Y Y.Study of element-free Galerkin method in the seismic forward modeling[J].Progress in Geophysics,2007,22(5):1539-1544

[15] 冯德山,王洪华,戴前伟.基于无单元Galerkin法探地雷达正演模拟[J].地球物理学报,2013,56(1):298-308 Feng D S,Wang H H,Dai Q W.Forward simulation of ground penetrating radar based on the element-free Galerkin method[J].Chinese Journal of Geophysics,2013,56(1):298-308

[16] 戴前伟,王洪华.基于随机介质模型的GPR无单元法正演模拟[J].中国有色金属学报,2013,23(9):1-9 Dai Q W,Wang H H.Element free method forward modeling of GPR based on random medium model[J].The Chinese Journal of Nonferrous Metals,2013,23(9):1-9

[17] 严家斌,李俊杰.无网格法在大地电磁正演计算中的应用[J].中南大学学报(自然科学版),2014,45(10):3513-3520 Yan J B,Li J J.Magnetotelluric forward calculation by meshless method[J].Journal of Central South University(Science and Technology),2014,45(10):3513-3520

[18] Liu G R,Gu Y T.A point interpolation method for two-dimensional solids[J].International Journal for Numerical Methods in Engineering,2001,50(4):937-951

[19] 李俊杰,严家斌.无网格点插值法大地电磁二维正演数值模拟[J].石油物探,2014,53(5):617-626 Li J J,Yan J B.Magnetotelluric two-dimensional for-

ward numerical modeling by meshfree point interpolation method[J].Geophysical Prospecting for Petroleum,2014,53(5):617-626

[20] 戴前伟,张富强,杨坤平,等.电导率分块线性变化的二维高频大地电磁法有限元正演模拟[J].物探化探计算技术,2012,34(5):552-558 Dai Q W,Zhang F Q,Yang K P,et al.The finite element method for modeling 2-D high-frequency electromagnetic with continuous variation of conductivity within each block[J].Computing Techniques for Geophysical and Geochemical Exploration,2012,34(5):552-558

[21] Zhdanov M S,Varentsov I M,Weaver J T,et al.Methods for modelling electromagnetic fields results from COMMEMI-the international project on the comparison of modelling methods for electromagnetic induction[J].Journal of Applied Geophysics,1997,37(3):133-271

[22] 许建荣.起伏地形条件下大地电磁测深二维正反演研究及应用[D].长沙:中南大学地球科学与信息物理学院,2010 Xu J R.Research and applications of 2-D MT forward modeling and inversion with topography[D].Changsha:Central South University of Geosciences and Info-Physics,2010

(编辑：顾石庆)

Magnetotelluric two-dimensional forward modelling by finite element-point interpolation coupling method

Li Junjie1,Yan Jiabin2

(1.ZhejiangDesignInstituteofWaterConservancyandHydroelectricPower,Hangzhou310002,China; 2.KeyLaboratoryofNonferrousResourcesandGeologicalHazardDetection,SchoolofGeosciencesandInfo-Physics,CentralSouthUniversity,Changsha410083,China)

Point interpolation method (PIM) is a typical global weak-form meshfree numerical calculation method.The physical properties of PIM are loaded on Gauss integral points which are only related with coordinates during geological modeling.Therefore,PIM is more convenient while dealing complex model than conventional grid method,but the former computation efficiency is low.We couple FEM and PIM into finite element-point interpolation method (FE-PIM) for magnetotelluric two-dimensional forward.Firstly,magnetotelluric two-dimensional discrete system matrix is deduced through substituting the shape function constructed by interpolation method and combining Galerkin method with Gauss integral formula.Then,the principle of background grid integral and the loading technique of boundary conditions are briefly characterized.Finally,the effectiveness and high efficiency of the FE-PIM algorithm and the convenience for complex models are proved by several numerical models.

point interpolation method,global weak-form meshfree method,magnetotelluric,finite element-point interpolation method

2014-12-02;改回日期：2015-02-15。

李俊杰(1989—),硕士,助理工程师,现主要从事大地电磁无网格化正演模拟研究工作。

国家自然科学基金项目(40874055)和湖南省自然科学基金项目(14JJ2012)共同资助。

P631

A

1000-1441(2015)04-0477-08

10.3969/j.issn.1000-1441.2015.04.015