基于压缩感知和TV准则约束的地震资料去噪

刘 伟,曹思远,崔 震

(1.中国石油大学(北京)油气资源与探测国家重点实验室,北京昌平102249;2.中国石油大学CNPC物探重点实验室,北京昌平102249)

基于压缩感知和TV准则约束的地震资料去噪

刘 伟1,2,曹思远1,2,崔 震1,2

(1.中国石油大学(北京)油气资源与探测国家重点实验室,北京昌平102249;2.中国石油大学CNPC物探重点实验室,北京昌平102249)

考虑到传统曲波变换阈值法难以获得理想的去噪效果,提出一种基于压缩感知和全变差(Total Variation,TV)准则约束的曲波变换地震资料去噪方法。该方法将传统的去噪问题转化成TV准则约束下的最优化问题,通过求取最优解重构原始信号,从而实现对地震资料的去噪处理。理论模型数据测试结果表明,该方法在地震资料去噪过程中可以有效压制同相轴边缘附近产生的不光滑畸变,相比传统的曲波变换阈值法能够获得更好的去噪效果;与F-X反褶积相比,该方法不仅能够有效压制地震资料中的随机噪声,提高地震资料的信噪比,而且能够较好地保护有效信号。某工区实际地震资料去噪结果进一步验证了上述方法的有效性。

压缩感知;TV准则;曲波变换;随机噪声;噪声衰减

地震信号在传播过程中不可避免地受到噪声的影响,使地震资料的品质降低,给后续解释工作带来困难；因此,提高地震资料信噪比是地震资料处理的主要任务之一。在实际生产中,常用的压制噪声的方法主要有F-X反褶积[1]、多项式拟合[2]、F-K滤波[3]、奇异值分解[4]和小波变换[5]等。然而这些方法在去噪处理过程中都不同程度地存在局限性,如作为全局变换的傅里叶变换对奇异点或奇异曲线的局部特征刻画不够准确,F-X反褶积使地震数据中的所有相干信息都加强,小波变换对于高维信号的边缘信息表达不够准确等,所有这些都极大地影响了地震资料的去噪效果。

压缩感知是近几年发展起来的一种新的图像处理方法[6-7],目前已经广泛应用于天文学、核磁共振和模式识别等领域,且得到了良好的发展。在医学信号检测、特征提取、故障诊断和图像融合等方面,压缩感知也是众多学者研究的热点[8]。该方法突破了Nyquist采样定理的限制,在一定条件下可以利用欠采样数据重构原始数据;利用地震数据在变换域中的稀疏特性,通过设定稀疏基矩阵和测量矩阵,可以将地震数据去噪问题转化成求解最优化问题。

用于地震数据稀疏表示的方法有很多,常用的有傅里叶变换、离散余弦变换、短时傅里叶变换、小波变换和曲波变换等[9]。傅里叶变换[10]和离散余弦变换[11]都是一种全局变换,不能有效地刻画信号的局部特征;短时傅里叶变换[12]是傅里叶变换的进一步发展,使用窗函数作用于信号后再进行傅里叶变换,本质上是一种单一分辨率分析方法;小波变换[13]继承并发展了短时傅里叶变换的局部化思想,可以根据待分析信号的特征自动调节窗口大小,从而实现对信号的多分辨率分析,但不能很好地用于具有曲线状特征的地震数据稀疏表示。近些年兴起的曲波变换[14]由不同尺度、不同方向的曲线元素构成变换基,在保持小波变换多分辨率特性的同时增加了小波变换的多方向性和各向异性,更加适用于刻画地震数据的特征,是对地震数据进行稀疏表示的理想工具。因此,曲波变换目前已经被广泛应用于多次波衰减[15]、地震数据去噪[16-17]、面波压制[18]和图像处理[19]等领域。

传统的曲波变换阈值法利用有效信号和随机噪声在曲波系数上的分布差异,选择合适的阈值函数对曲波系数进行阈值处理,通过曲波反变换得到去噪后的结果。这种方法在去除噪声的同时使信号边缘附近产生了不光滑畸变现象,且对有效信号局部造成一定损伤。本文基于压缩感知理论,在全变差(TV)准则约束下,将传统去噪问题转化成求解最优化问题,通过最优解重构原始信号,从而实现对地震资料的去噪处理。该方法能够有效压制同相轴边缘附近产生的不光滑畸变,较好地衰减地震数据中的随机噪声,最大限度地保留有效信号,从而为地震数据的高保真处理奠定基础。

1 基本原理

1.1 压缩感知理论

信号的压缩重建问题可以描述为由一组不完整的数据通过算子作用恢复出完整的数据，即：

(1)

其中,y∈RM为测得的不完整数据,f∈RN为期望恢复的数据,ψ∈RM×N(N>M)为测量矩阵,n∈RM为噪声。

由于N>M,即方程的个数少于未知数的个数,因此,这是一个欠定问题,也就是说方程(1)的解不唯一。压缩感知理论为求取f提供了可能,但要求满足3个条件：①f是稀疏的,或者在某个变换域内是稀疏的;②采用随机采样,使假频转换成容易压制的噪声而将其滤除;③使用有效的求解策略寻找最优解。

如果f在某个变换域中的系数x是稀疏的,即x=Φf(Φ为稀疏变换基矩阵),则(1)式可以写成如下形式：

(2)

在压缩感知理论框架下,信号的恢复问题可以表示为基于L0范数最小化的稀疏优化问题，即：

(3)

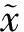
(3)式本质上是一个NP难问题[20],Donoho[21-22]采用最小L1范数代替最小L0范数的方法来求解,即：

(4)

信号f可以通过(5)式来重建：

(5)

在信号重建过程中,首先要保证测量矩阵ψ和稀疏变换基矩阵Φ非相干,其次,测量矩阵ψ要满足有限等距特性[21]。因此,文中稀疏变换基矩阵选用曲波变换基矩阵,测量矩阵选用高斯随机矩阵[22]。

1.2 稀疏变换

稀疏变换是压缩感知的重要组成部分,变换域中的数据越稀疏,重构效果就越好。本文使用对于地震数据的表示具有独特优势的曲波变换作为稀疏变换。曲波变换正变换可以简单地表示成信号f与曲波φj,l,k的内积[19]：

(6)

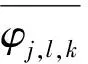
由(6)式可知,给定一个曲波函数,经过伸缩、平移和旋转,可以生成平方可积函数空间的紧标架,这就意味着它具有如下重构公式：

(7)

1.3 基于压缩感知和TV准则约束的地震数据去噪原理

令含有噪声的地震数据表示为：

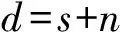
(8)

式中：d为含噪数据;s为有效信号;n为随机噪声。

首先通过一个M×N维(M≪N)的测量矩阵ψ作用于含噪数据d,使其从N维(高维)信号投影到M维(低维)信号y:

(9)

然后对含噪数据d进行稀疏变换：

(10)

将(9)式和(10)式整理得到：

(11)

对于含噪数据d而言,有效信号s在稀疏变换域内是稀疏的,但是噪声n是不稀疏的,根据压缩感知理论,通过估计有效信号的稀疏表示来重建原始数据,可以达到去噪的目的。上述过程等价于求解如下最优化约束问题：

(12)

(13)

式中：n1和n2为x的维数。

这样,根据拉格朗日法则,公式(12)可转化成如下无约束的正则化问题[23]：

(14)

通过基于压缩感知的TV重构TVAL3算法[23]求解方程(14),地震数据去噪后的结果可以表示为：

(15)

2 数值模型试算

2.1 合成记录A

首先建立如图1a所示的合成地震记录A,该记录共50道,60个采样点,采样率为1ms,加入随机噪声之后的地震记录如图1b所示。图2a为传统的曲波变换阈值法去噪结果,图2b为本文基于压缩感知和TV准则约束的曲波变换(以下简称为TV准则约束的曲波变换)去噪结果。对比图2a和图2b可以发现,两种方法都能够对地震记录中的随机噪声进行有效压制,但是,传统的曲波变换阈值法在去除噪声的同时,使同相轴边缘附近产生了不光滑畸变现象(椭圆区域所示),严重影响了去噪效果;而基于TV准则约束的曲波变换能够有效地压制同相轴边缘附近的不光滑干扰,去噪效果更好。此外,传统的曲波变换阈值法使非有效信号区域变得模糊,而TV准则约束的曲波变换在这些区域较好地保持了原始数据的特征。

图1 合成记录A(a)及加噪后记录A(b)

图2 传统的曲波变换阈值法去噪(a)和TV准则稀疏约束的曲波变换去噪(b)效果对比

2.2 合成记录B

为了说明TV准则约束的曲波变换具有更好的去噪效果和保幅能力,建立如图3a所示的合成地震记录B,该记录共50道,512个采样点,采样率为2ms,图3b为该记录加入随机噪声后的结果。图3c和图3d分别为F-X反褶积和TV准则约束的曲波变换去噪结果。对比图3c和图3d可见,前者虽然可以压制绝大多数的随机噪声,但是去噪后的结果信噪比降低,去噪效果不够理想;而TV准则约束的曲波变换去噪结果不仅有效压制了随机噪声,而且信噪比较高,去噪效果更好。图3e 和图3f为两种方法去噪前、后的残差剖面,可见F-X反褶积的残差剖面上有效同相轴隐约可见,尤其是弯曲同相轴和相交同相轴(图3e椭圆区所示),说明F-X反褶积对有效信号的损伤较大;相比而言,TV准则约束的曲波变换去除的噪声里几乎没有有效同相轴的痕迹,说明该方法在去噪过程中对有效信号的损伤相对较小。

为了更好地评价F-X反褶积与TV准则约束的曲波变换去噪效果,定义如下参数：

1) 信噪比

(16)

2) 峰值信噪比

(17)

(16)和(17)式中：s0为无噪声数据;s为含噪声数据;M为数据矩阵的行数;N为数据矩阵的列数。

3) 均方差

(18)

4) 平均绝对误差

(19)

(18)和(19)式中：f(m,n)为去噪后数据;f0(m,n)为无噪声数据;M为数据矩阵的行数;N为数据矩阵的列数。

5) 去噪能力

(20)

其中,RSN为去噪后数据的信噪比，RSN0为原含噪数据的信噪比，EN0为原含噪数据中噪声的能量，EN为去噪后数据中噪声的能量。

表1是合成记录B分别使用F-X反褶积和TV准则约束的曲波变换去噪处理后计算得到的信噪比RSN,峰值信噪比RPSN,均方差SMS,平均绝对误差SMA和去噪能力AD。由表1可知,TV准则约束的曲波变换方法提高信噪比的能力更强,在信号保真方面也比F-X反褶积有优势。总体而言,TV准则约束的曲波变换去噪能力(0.0661)明显优于F-X反褶积(0.0342),而且去噪过程中对有效信号的损伤也相对较小。

图3 TV准则约束的曲波变换与F-X反褶积去噪效果分析

表1 不同方法去噪结果评价参数对比

评价参数F⁃X反褶积TV准则约束的曲波变换RSN/dB7．33478．9837RPSN/dB20．042521．8914SMS0．00440．0017SMA0．03850．0163AD0．03420．0661

3 实际资料处理效果分析

为了进一步测试本文方法在实际地震资料处理中的应用效果,选取某工区实际含噪声地震资料进行TV准则约束的曲波变换,并与传统的F-X反褶积进行对比。图4为研究区某实际单炮记录,共150道,每道750个采样点,采样率为2ms。可以看出,随机噪声的存在使得该炮集数据的信噪比较低,同相轴连续性较差,尤其在800～1200ms,一些有效同相轴被完全淹没在噪声之中。图5a 是基于TV准则约束的曲波变换去噪结果,可见随机噪声得到了有效压制,同相轴清晰、连续(图5a中矩形框所示),位于800～1200ms的有效同相轴也得到恢复,炮集数据整体信噪比得到明显提高。图5b为F-X反褶积去噪结果,可见大部分随机噪声也得到压制,但是仔细对比图5a与图5b不难发现TV准则约束的曲波变换去噪效果更好。图6是TV准则约束的曲波变换与F-X反褶积压制的噪声剖面,可见F-X反褶积压制的噪声剖面上弯曲同相轴和倾斜同相轴隐约可见,说明该方法对有效信号造成了一定程度损伤;而TV准则约束的曲波变换压制的噪声剖面基本没有有效同相轴的痕迹,说明该方法对有效信号的损伤较小。

图4 某工区实际单炮记录(含噪)

图5 某工区含噪炮集TV准则约束的曲波变换(a)与F-X反褶积(b)去噪结果对比

图6 某工区含噪炮集TV准则约束的曲波变换(a)与F-X反褶积(b)去除的噪声对比

图7为研究区去噪前叠加剖面,共1000道,时间为1000～1325ms,采样率为2ms。图8a为TV准则约束的曲波变换去噪结果,可以看出1150～1250ms及1260～1310ms处(图8a中矩形框所示)断面变得更加清晰,一些淹没在噪声之中的同相轴也显现出来,而且同相轴更加连续(图8a 中椭圆框所示)。作为对比,应用F-X反褶积对该数据进行了处理(图8b),两种方法去掉的噪声分别如图9a和图9b所示。由图7至图9可见,与叠前炮集去噪类似,TV准则约束的曲波变换和F-X反褶积都可以压制随机噪声,但是前者的去噪效果更好,对有效同相轴的损伤更小,从而为地震资料后续处理奠定了良好的基础。

图7 研究区含噪地震剖面

图8 研究区含噪地震剖面TV准则约束的曲波变换(a)与F-X反褶积(b)去噪结果对比

图9 研究区含噪地震剖面TV准则约束的曲波变换(a)与F-X反褶积(b)去除的噪声对比

4 结论与认识

本文将压缩感知和TV准则与曲波变换结合起来,提出了一种基于压缩感知和TV准则约束的曲波变换地震资料去噪方法,通过理论模型测试和实际资料处理,可以得到以下结论与认识。

1) 与传统的曲波变换阈值去噪方法相比,基于压缩感知和TV准则约束的曲波变换去噪方法在去除噪声的同时可以很好地压制同相轴边缘附近产生的不光滑畸变,有效改善去噪效果。

2) 与F-X反褶积相比,基于压缩感知和TV准则约束的曲波变换去噪方法不仅能够很好地压制地震资料中的随机噪声,而且能够减少对有效信号的损伤。

3) 无论对于炮集数据还是对于叠加剖面,基于压缩感知和TV准则约束的曲波变换都是一种有效的去噪方法。

基于曲波变换求解最优化解是本文方法的核心,对计算机硬件有较高的要求,如何实现并行算法以提高计算效率,是我们需要进一步研究的内容。

[1] 康治,于承业,贾卧,等.f-x域去噪方法研究[J].石油地球物理勘探,2003,38(2)：136-138 Kang Z,Yu C Y,Jia W,et al.A study on noise suppression method in f-x domain [J].Oil Geophysical Prospecting,2003,38(2):136-138

[2] Yu S,Cai X,Su Y.Seismic signal enhancement by polynomial fitting [J].Applied Geophysics,1989,1(1):57-65

[3] 张军华,吕宁,田连玉,等.地震资料去噪方法综合评述[J].石油地球物理勘探,2005,40(增刊)：121-127 Zhang J H,Lv N,Tian L Y,et al.Comprehensive review of seismic data denoising[J].Oil Geophysical Prospecting,2005,40(S1):121-127

[4] 刘伟,杨凯,王征,等.基于SVD的正交多项式变换及其在地震资料处理中的应用[J].工程地球物理学报,2010,7(4):433-437 Liu W,Yang K,Wang Z,et al.Orthogonal polynomials transform based on SVD and its application in seismic data processing[J].Chinese Journal of Engineering Geophysics,2010,7(4):433-437

[5] 王勇,郦军,张奎凤.基于小波变换的地震信号降噪处理[J].石油物探,1998,37(3)：72-76 Wang Y,Li J,Zhang K F.The noise elimination processing of seismic signal based on wavelet transform [J].Geophysical Prospecting for Petroleum,1998,37(3):72-76

[6] Canales E J,Wakin M B.An introduction to compressive sampling [J].IEEE Signal Processing Magazine,2008,25(2):21-30

[7] Donoho D L.Compressed sensing [J].IEEE Transactions on Information Theory,2006,52(4):1289-1306

[8] 尹宏鹏,刘兆栋,柴毅,等.压缩感知综述[J].控制与决策,2013,28(10)：1441-1445 Yin H P,Liu Z D,Chai Y,et al.Survey of compressed sensing [J].Control and Decision,2013,28(10):1441-1445

[9] Shan H,Ma J W,Yang H Z.Comparisons of wavelets,contourlets and curvelets in seismic denoising[J].Journal of Applied Geophysics,2009,69(2):103-115

[10] Bochner S,Chandrasekharan K.Fourier Transforms [M].New Jersey:Princeton University Press,1949:45-52

[11] Feig E,Winograd S.Fast algorithms for the discrete cosine transform[J].IEEE Transactions on Signal Processing,1992,40 (9):2174-2193

[12] Chikkerur S,Cartwright A N,Govindaraju V.Fingerprint enhancement using STFT analysis[J].Pattern Recognition,2007,36(2):303-312

[13] Rioul O,Vetterli1 M. Wavelet and signal processing [J].IEEE Signal Processing,1991,8 (4):14-37

[14] Candès E J,Demannet S L,Donoho D L,et al.Fast discrete curvelet transforms[J].SIAM Multiscale Modeling and Simulation,2006,5(3):861-899

[15] Herrmann F J,Verschuur E.Curvelet-domain multiple elimination with sparseness constraints [J].Expanded Abstracts of 74thAnnual Internat SEG Mtg,2004,1333-1336

[16] 张恒磊,张云翠,宋双,等.基于Curvelet 域的叠前地震资料去噪方法[J].石油地球物理勘探,2008,43(5)：508-513 Zhang H L,Zhang Y C,Song S,et al.Curvelet domain-based prestack seismic data denoise method[J].Oil Geophysical Prospecting,2008,43(5):508-513

[17] 仝中飞,王德利,刘冰.基于Curvelet 变换阈值法的地震数据去噪方法[J].吉林大学学报(地球科学版),2008,38(增刊)：48-52 Tong Z F,Wang D L,Liu B.Seismic data denoise based on curvelet transform with the threshold method [J].Journal of Jilin University (Earth Science Edition),2008,38(S1):48-52

[18] 董烈乾,李振春,王德营,等.第二代Curvelet变换压制面波方法[J].石油地球物理勘探,2012,46(6)：897-904 Dong L Q,Li Z C,Wang D Y,et al.Ground-roll suppression based on the second generation Curvelet transform [J].Oil Geophysical Prospecting,2012,46(6):897-904

[19] Ying L,Demanet L,Candes E.3D discrete curvelet transform [J].International Society for Optics and Photonics,2005,SPIE591413

[20] Amaldi E,Kann V.On the approximability of minimizing nonzero variables or unsatisfied relations in linear systems [J].Theoretical Computer Science,1998,209(1):237-260

[21] Donoho D.For most large underdetermined systems of linear equations,the minimal l1-norm near-solution approximates the sparsest near-solution [J].Communications on Pure and Applied Mathematics,2006,59(6):797-829

[22] Donoho D.Compressed sensing [J].IEEE Transactions on Information Theory,2006,51(4):1289-1306

[23] Li C B.An efficient algorithm for total variation regularization with applications to the single pixel camera and compressive sensing [D].USA：Rice University,2009

(编辑：戴春秋)

Random noise attenuation based on compressive sensing and TV rule

Liu Wei1,2,Cao Siyuan1,2,Cui Zhen1,2

(1.StateKeyLaboratoryofPetroleumResourcesandProspecting,ChinaUniversityofPetroleum,Beijing102249,China; 2.CNPCKeyLabofGeophysicalProspecting,ChinaUniversityofPetroleum,Beijing102249,China)

Owing to the undesired noise attenuation effect of conventional threshold method based on Curvelet transform,a seismic data denoising approach based on compressive sensing and Total Variation (TV ) rule is proposed in this paper.It changes noise attenuation into the optimization problem under the constraint of TV rule,the original signal is reconstructed by optimum solution and thereby the denosing results of seismic data are obtained.Theoretical numerical model test shows the proposed method can not only effectively suppress the distortion near the edges of seismic events but also achieve better results compared with conventional Curvelet transform threshold method.Moreover,compared with F-X deconvolution,this approach can attenuate the random noise effectively and preserve effective signal with an improvement of signal to noise ratio in seismic data.Finally,the denoising results of actual seismic data prove the effectiveness of the proposed method further.

compressive sensing,TV norm,Curvelet transform,random noise,noise attenuation

2014-09-28;改回日期：2014-12-18。

刘伟(1982—),男,博士在读,主要从事地震数据处理新方法研究和储层预测工作。

国家科技重大专项(2011ZX05024-001-01)和国家自然科学基金项目(41140033)共同资助。

P631

A

1000-1441(2015)02-0180-08

10.3969/j.issn.1000-1441.2015.02.009