倾角成像道集中反射波和绕射波特征分析及成像质量改善方法研究

徐 辉

(中国石油化工股份有限公司胜利油田分公司物探研究院，山东东营257022)

倾角成像道集中反射波和绕射波特征分析及成像质量改善方法研究

徐 辉

(中国石油化工股份有限公司胜利油田分公司物探研究院，山东东营257022)

岩性储层识别和评价是东部探区的重要勘探任务，高质量的成像道集是做好岩性储层识别和评价的基础数据。地层倾角成像道集是不同于张角成像道集的一种对成像结果的高维表征方法，与张角成像道集结合可以更好地表征有效反射能量在反射点处的传播方向、分布范围及其随方位角的变化等。从张角和地层倾角成像道集中反射波和绕射波的特征入手，分析了反射波和绕射波在两种道集中的区别与联系。指出了利用倾角成像道集的角度分布特征进行滤波器设计，可以滤除该成像道集中与反射界面倾角不相符的成分，达到提高成像质量，保真反射特征的目的。最后，通过理论模型数值试验证明这一成像质量改善方法的正确性及实用性。

张角成像道集;倾角成像道集;倾角滤波;成像质量

随着岩性油气藏在我国油气勘探中所占的比例越来越高，对岩性油气藏精细成像的需求越来越迫切。常规针对构造油气藏勘探的方法技术在描述岩性油气藏时达不到精度要求或不适用。因此，需要发展针对岩性油气藏勘探的成像方法与技术。保真的角度成像道集是从面向构造油气藏勘探发展到面向岩性油气藏勘探的必要桥梁。

地震数据的完整表达应该是7维数据空间d(xs,px,ys,py,zs,pz,t)，其中，xs,ys,zs分别为炮点的x,y,z坐标，px,py,pz分别是x,y,z方向的射线参数，t为双程旅行时。地震波成像结果的完整表达也应该在7维成像空间I(x,y,z;γ,ψγ;α,ψα)，其中，x,y,z分别是成像点的坐标，γ,ψγ分别是地震波入射和反射半张角及其对应的方位角，α,ψα分别是地层倾角及其对应的方位角。成像结果中原则上既包括方位张角成像道集(前5维)，也包括方位倾角成像道集,但是，当前国内外常规处理软件中，叠前深度偏移模块大多只能输出地表偏移距成像道集，而且是不分方位的。

Schleicher等[1]基于出射角和剖面上反射层倾角约束来产生7维成像道集。事实上，逆时深度偏移(RTM)也可以输出张角和倾角成像道集[2-3]，但是计算量太大。已知波传播方向的Beam叠前深度偏移应该是产生7维成像道集的合适方法。由Snell定律可知，出射角和地下倾角唯一确定了反射路径。倾角成像道集中反射波成像(拟)双曲线的顶点位于真反射界面倾角处，以此可以设计倾角滤波器，在输出的成像道集上进行优化。在角度域进行Kirchhoff叠前深度偏移也能实现上述思路，改善成像质量[4]。通常，叠前深度偏移只输出反射角道集而忽略地层倾角道集。实际上，地层倾角道集可以更好地表征地下有效反射能量。在倾角成像道集中，反射波成像和绕射波成像的特征是不同的，倾角成像道集的输出同样也可以改善散射成像的质量。

本文从地下张角成像道集和地层倾角成像道集中反射波和绕射波的特征入手，分析了反射和绕射在两种成像道集中的区别与联系，指出保真的角度成像道集是走向岩性油气藏勘探的十分关键的基础数据。在此基础上，对角度域成像过程中提取得到的倾角道集使用倾角滤波来实现限孔径的Kirchhoff叠前深度偏移，达到提高成像质量和保真反射特征的目的。最后，通过理论模型数值试验证明本文成像质量改善方法的正确性及实用性。

1 成像道集中反射波和绕射波像的特征分析

地震波成像结果可以表示在方位张角道集中，也可以表示在方位倾角道集中。表达在方位张角道集中的成像结果可以用于进行偏移速度和各向异性参数分析，或者进行裂隙储层特征分析。但是，表达在倾角成像道集中的成像结果及其用途却涉及较少，需要对其几何特征甚至动力学特征进行分析，为后续的应用奠定基础。

1.1 地表偏移距道集和张角成像道集中剩余曲率关系分析

对于水平层状介质，速度的正确与否仅仅影响偏移成像结果的深度，不会改变反射波的到达时。称此为时间相等原理。

在真速度场中，时距关系为：

(1)

其中，z为反射界面真深度，h为炮检半偏移距，v为真实速度场。在偏移速度场中，时距关系为：

(2)

其中，vm为偏移速度场，zm为反射界面的偏移深度。依据时间相等原理，可以推导出(3)式：

(3a)

(3b)

式中：γ=vm/v，v为真实速度。当γ>1时，(3b)式是一个双曲方程;当γ=<1时，(3b)式是一个椭圆方程;当γ=1时，zm=z。

(3a)式代表不同(地表)偏移距的反射波在深度成像空间的位置，实质上它规定了一个成像空间中的深度-偏移距关系，就是一个偏移距成像道集的表现形式。

当偏移速度正确时，偏移距成像道集表现为一个拉平的道集;当偏移速度小于正确的速度时，偏移距为0时的成像深度小于真深度，且非零偏移距成像道集表现为向上的椭圆形式的道集;当偏移速度大于正确的速度时，偏移距为0时的成像深度大于真深度，且非零偏移距成像道集表现为向下的双曲形式的道集。这是在偏移距成像道集中进行剩余速度分析或层析反演的理论基础。

偏移距总是对应一定的张角。常速介质假设下，(3b)式变为：

(4)

其中，α代表半张角。由(4)式可知，张角成像道集与(地表)偏移距成像道集的表现形式是一样的。但是，角度与偏移距的剩余深度差不同，这也是用张角成像道集和偏移距成像道集进行深度速度估计需要不同公式的原因。

对于非水平层状介质，波的传播角度与成像道集中张角和界面倾角的关系如图1所示。

非水平层状介质真速度场的时距关系为：

(5)

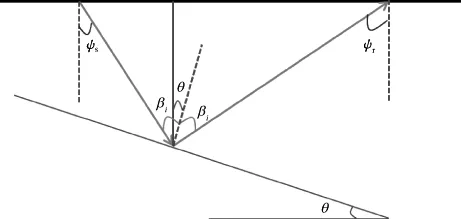
图1 非水平层状界面情况下波的传播角度与成像道集中张角和界面倾角的关系

其中，xs为炮点坐标，xr为检波点坐标，xi为地下反射点坐标。对非水平层状介质，偏移速度的正确与否仅仅影响偏移成像结果的深度和横向位置，不会改变反射波的到达时，因此有：

(6)

其中，xm为地下成像点坐标。由(5)式和(6)式可得：

(7)

由公式(7)推导出显式的深度-距离关系是很困难的。根据图1，可以用波的出射和到达角度重新表达公式(7)：

(8)

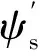
(9)

其中，β和θ分别为地下真入射半张角和地下界面真倾角，β′和θ′分别为偏移时入射半张角和地下界面倾角。(9)式表达了一个张角道集。

1.2 张角成像道集与倾角成像道集中反射波和绕射波像的特征分析

假若地下是一个散射点，在偏移距或张角成像道集中，由于(5)式、(6)式和(7)式也是成立的，则该两种成像道集中散射点与反射点的像的几何特征是相同的。简单地讲就是拉平、上凹和下凸，利用其中的剩余深度差可以进行速度估计。

但是，分析可知，成像道集也可以表达在(反射界面的)倾角域。与前述张角成像道集中反射波和绕射波像的深度-距离(张角)关系的一致性不同，在倾角成像道集中，反射波和绕射波像的表现特征是不同的。

如图1所示，(9)式可以改写为：

(10)

把(9)式直接写成(10)式说明了张角和倾角之间是一对一映射的关系，叠前偏移成像过程中也是按照一对一映射的含义来产生这两种道集。(10)式表达了一个倾角道集，描述了绕射波和反射波像的深度-倾角关系。

对绕射波而言，在张角成像道集和倾角成像道集中的几何特征是一样的。但是，对反射波而言，在张角成像道集和倾角成像道集中的几何特征是不同的。正是有这样的差异，才发展出了倾角成像道集中的绕射波像和反射波像的分离方法。实质上，当速度正确时，在张角成像道集中拉平的成像道集，在倾角成像道集中，变成一条双曲线，这可以被视为一个Radon变换。

另一方面，实际情况下反射波像的深度-倾角关系不仅仅是一个基本由反射界面倾角决定的像，而是在该倾角周围展布的一条曲线，这正是(10)式所预计的。

图2展示了上述理论分析。图2a是地质模型示意图，其中有一个绕射点(星号表示)，两个反射界面，一个倾斜，另一个水平。其中绿色的垂线代表产生成像道集的位置。图2b代表张角成像道集，因为偏移速度正确，绿色垂线上的绕射点和反射点的张角道集都被拉平。但是，在图2c(倾角成像道集)中，绕射点的不同倾角的像是排齐的，反射点的深度-倾角曲线表现为拟双曲形式，顶点位于反射界面的真倾角处。

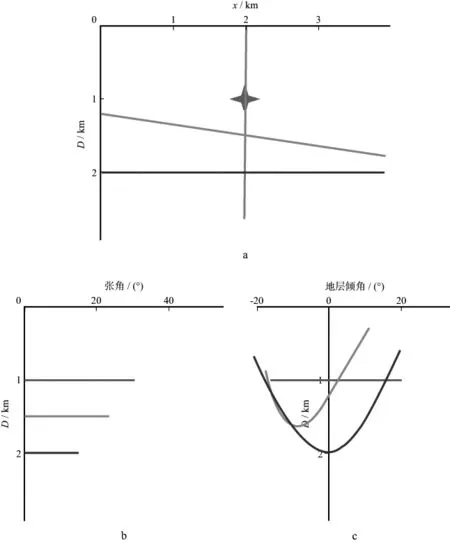
图2 绕射波和反射波在张角和倾角成像道集中的表现形式

为了解释反射点的像在倾角道集中出现在真倾角处的原因，从自激自收地震道的偏移成像过程来说明。对于自激自收地震道的偏移，图3给出了偏移响应曲线，可以用公式(11)表达为：

(11)

常数情况下，偏移响应是一个半圆，半圆上任意点的倾角可以定义为：

(12)

把xm=-zmtanθ代入(12)式可以得到(zm,θ)满足的方程：

(13)

其中，θ是反射界面的倾角。可以看出，(13)式定义了自激自收地震道在倾角域的偏移响应曲线，如图4所示。非零偏移距地震道在倾角域的偏移响应曲线与此类似。因此，当地下存在一个特定角度的反射界面时，不同偏移距地震道在倾角域的干涉成像结果是在真反射界面倾角处出现干涉加强的像。

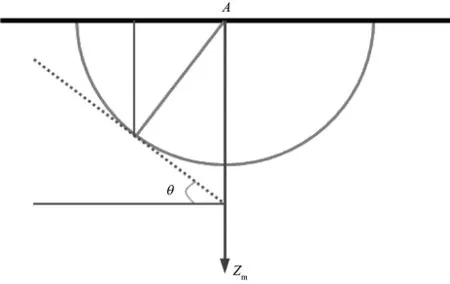
图3 自激自收地震数据的偏移响应

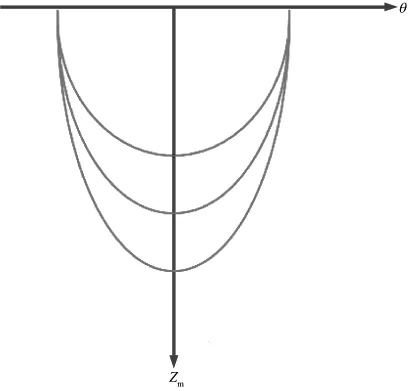
图4 倾角-深度域中自激自收地震数据偏移响应曲线

一般地，成像结果仅仅集中在真反射界面倾角周围，其它角度的像是没有干涉掉的结果，但它们会影响最后的成像结果，降低成像质量。据此可以设计反射倾角滤波器，综合Fresnel带效应把非地质倾角的假象滤除，提高最后叠加成像的质量。

2 张角成像道集与倾角成像道集的生成方法

提取角度道集的算法需要计算角度参数，角度参数的计算可以在波动理论框架下借助于波场局部方向分解得到[5]，也可以在射线理论框架下通过计算旅行时的空间梯度得到。如图5所示，三维情况下，入射慢度矢量PS和散射慢度矢量PR共同描述了散射点处波的传播方向特征[6]。入射与散射慢度矢量之和PM称为照明矢量。照明矢量和Z轴正方向的夹角就是照明倾角(ϑ)。该倾角和地层倾角是相等的。描述角度域方向特征的4个角度分别是：入射角θ(局部入射与界面法线夹角)、方位角φ(局部入射和散射慢度PS，PR所在平面的方位角)、照明倾角ϑ(局部照明矢量和Z轴的夹角)、散射方位角ψ(即照明矢量PM所在平面的方位角)。S，R和D分别代表炮点、检波点和地下反射点。

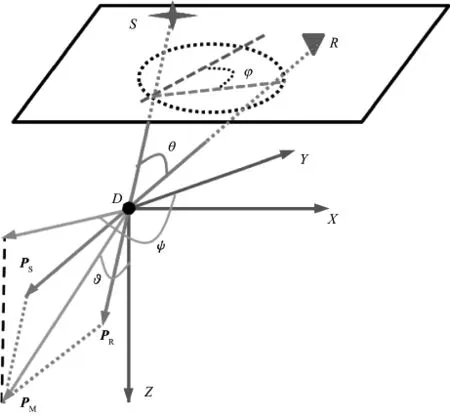
图5 散射点处地震波传播角度示意图解

角度域共成像点道集的提取需要计算反映入射方向与散射方向特征的角度参数。利用最大能量法或动态规划法计算得到炮点和检波点旅行时场[7-8]，计算旅行时场的梯度方向，进而得到炮、检点入射方向PS和PR，三维情况下，PS和PR的计算公式可以表示为：

(14)

(15)

其中，Ts和Tr分别为炮点和检波点的旅行时场。利用PS和PR可计算得到入射角θ，方位角φ，地层倾角ϑ和散射方位角ψ[9]：

(16a)

(16b)

(16c)

(16d)

通过计算得到表示入射与散射方向特征的角度参数，根据后续分析的需要，沿所需的角度方向叠加可得到相应的角度域共成像点道集。

3 基于倾角成像道集的PSDM成像质量改善方法

张角成像道集中，当偏移速度比较正确时，对于反射点处某一倾角的反射界面，无论用何种张角或偏移距数据进行成像，其结果应仅仅出现在真地质倾角上或其附近。但是，由于地震数据的不规则、偏移速度不正确等因素的影响，必然会造成不同张角的像不能很好地互相干涉，在偏离真地质倾角较远的角度上还有未干涉掉的假象，它们会影响最终叠加成像的质量[10-11]。但是，倾角道集中正确的像应仅仅出现在真地质倾角或附近，据此可以设计地质倾角约束的滤波器，把远离真地质倾角的假象滤除，提高叠加成像的质量。

这样的处理在张角成像道集中是做不到的。张角成像道集中，一般是用切除和排齐的方法强行拉平道集来提高叠加成像的质量。但是，张角道集拉平与否是取决于速度，任意拉平道集并不能得到正确的、高质量的图像。因此，在倾角成像道集上设计地质倾角约束滤波器可以更合理地压制成像噪声，提高反射波的成像质量。相辅相成地，也可以设计合理的滤波器专门提高绕射波的成像质量[12]。

关于限制孔径的Kirchhoff叠前深度偏移[13]，很多学者都提出了自己的方法，以此来达到改善偏移成像质量的目的[14]。Schleicher等将偏移孔径和Fresnel带联系起来[15]，地震数据的叠加在该带内完成，实现所谓的保幅成像[16];Audebert等[17]基于出射角和剖面上反射层倾角约束来实现，利用Snell定律，出射角和倾角唯一确定了反射路径，以此来提取与绕射波时距曲线相切的地震数据。本文利用在成像过程中提取得到的倾角道集来实现限孔径的Kirchhoff叠前深度偏移。

在Kirchhoff PSDM中，利用动态规划法得到旅行时场，以此为基础利用第2节中(14)式和(15)式计算得到炮、检点旅行时场在各方向上的旅行时梯度，合成得到地下介质点上的局部入射和散射矢量方向，再利用(16c)式计算地层倾角，沿各个倾角进行角度叠加进而得到地层倾角域的共成像点道集。

在速度模型正确的情况下，倾角道集中的绕射波时距曲线为水平同相轴(绕射点正上方);反射波时距曲线为拟双曲线形状，并且顶点对应的角度为反射层倾角。图6为洼陷模型的Kirchhoff叠前深度偏移剖面，该剖面上存在4个反射界面，第3层反射界面存在倾角(±18°)。图7为图6所示剖面上CDP700，CDP900和CDP1100对应的倾角道集。由图7可见，真正贡献于积分法叠加成像的部分位于拟双曲线顶点处(红框标识内)，该部分对应绕射波时距曲线相切的地震数据。为此，在倾角道集上进行滤波处理，可以实现限孔径的Kirchhoff叠前深度偏移。该积分法公式可以表示为：

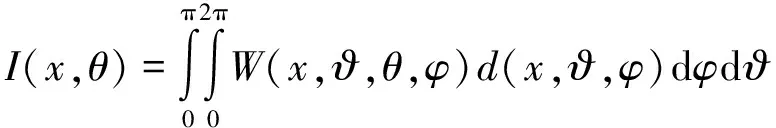
(17)

其中，W表示权函数，d表示地震数据。

图6 洼陷模型Kirchhoff叠前深度偏移剖面

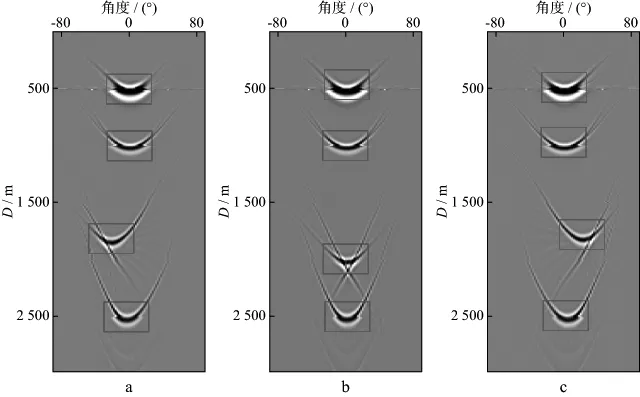
图7 洼陷模型Kirchhoff叠前深度偏移剖面上CDP700(a)，CDP900(b)和CDP1100(c)对应的倾角道集

如何在倾角道集上进行滤波处理呢？有的学者提出：先在偏移后的剖面上拾取反射界面倾角，之后利用拾取得到的反射界面倾角来设计滤波器[18]。本文为了在一次偏移中实现倾角道集的滤波，采用了以下做法：我们发现顶点处的同相轴近似水平，即在该点处，倾角为0，利用该性质，将斜率转换为角度，从而设计倾角滤波器。为了防止边缘截断效应对叠加剖面造成的影响，我们采用了Gauss衰减函数：

(18)

其中，δ=A/3(A为滤波器的角度阀值)，角度绝对值大于A的权系数为1%。

具体实现方法如下：

1) 进行角度域Kirchhoff叠前深度偏移，计算旅行时场梯度，合成地下局部入射和散射矢量方向Ps和Pr;

2) 利用Ps和Pr计算倾角，进而输出地层倾角道集;

3) 对得到的倾角道集进行斜率扫描，并将扫描的结果转换为倾角;

4) 结合扫描得到的倾角，利用Gauss衰减函数对倾角道集进行滤波;

5) 叠加滤波后的倾角道集，得到改善成像质量后的叠加剖面。

4 数值试验

为了验证本文方法的有效性，采用图8所示的模型对本文方法进行数值试验。模型中包含若干反射层和4个绕射点。图9a是Kirchhoff叠前深度偏移产生的倾角成像道集;图9b是在该倾角道集上扫描得到的倾角信息，目的是得到拟双曲线顶点的倾角及其附近角度像的展布情况，据此设计倾角滤波器;图9c是滤波器滤波后的倾角成像道集，对每一个CDP对应的倾角成像道集进行滤波后叠加，可以显著地改善叠加成像剖面的质量。图10a是没有进行倾角滤波的偏移叠加成像剖面;图10b是通过倾角滤波后的偏移叠加成像剖面。对比图10a 和图10b可见，图10a上由于倾角道集中干涉不彻底而产生的偏移叠加噪声，经过倾角滤波处理，被很大程度的压制，叠加剖面上的偏移“画弧效应”也被压制了(图10b)，可以看出倾角成像道集中的倾角滤波对提高成像质量有明显的作用。事实上，利用倾角成像道集上反射波像与绕射波像的深度-张角关系的差异，还可以单独提取绕射波进行成像，这对于强化绕射波的成像是很有利的。

图8 速度模型

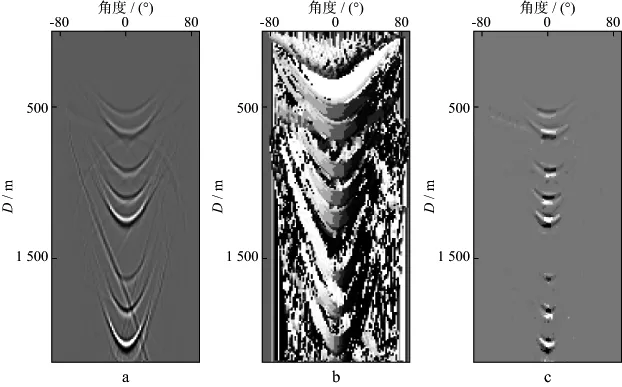
图9 模型倾角道集(a)、扫描得到的倾角(b)和滤波后的倾角道集

图10 原始模型偏移成像剖面(a)和改善成像质量后的偏移成像剖面(b)

5 结束语

高精度的面向储层的成像是成像技术发展的方向，保真的成像道集是关键的基础数据。叠前深度偏移若输出7维成像道集，可以看出在张角成像道集和地层倾角成像道集中反射波和绕射波像的不同特征。倾角成像道集中反射波的像应仅仅出现在真地质倾角处，偏离真倾角较远的角度上的假象会降低偏移叠加剖面的质量，这是设计倾角滤波器提高反射波成像质量的基本思想。另外，在倾角成像道集中，绕射波表现为拉平的同相轴，通过强化拉平可以改善绕射波成像质量，这对小尺度油气储层的描述是很有帮助的。

基于7维方位张角和方位地质倾角的成像道集进行面向储层，尤其是散射体储层(孔洞、不整合面、火山岩储层等)以及裂隙(缝)储层的研究是今后地震波成像的重点发展方向。

[1] Schleicher J,Hubral P,Tygel M,et al.Minimum apertures and fresnel zones in migration anddemigration[J].Geophysics,1997,62(3):183-194

[2] James E,Rickett J R,Sava P C.Offset and angle domain common image-point gathers for shot-profile migration[J].Geophysics,2002,63(3):883-889

[3] Sava P C,Fomel S.Angle-domain common-image gathers by wavefield continuation methods[J].Geophysics,2003,68(3):1065-1074

[4] 刘太臣.绕射波分离与成像方法研究[D].上海：同济大学，2013 Liu T C.The study of diffraction separation and imaging[D].Shanghai:TongJi University,2013

[5] Prucha M,Biondi B,Symes W.Angle-domain common image gathers by wave-equation migration[J].Expanded Abstracts of 69thAnnual Internat SEG Mtg,1999,824-827

[6] 程玖兵，马在田.针对目标的方位保真局部角度域成像方法[J].石油地球物理勘探,2011,46(3):374-385 Cheng J B,Ma Z T.True-amplitude azimuth targeted imaging method in local angle domain[J].Oil Geophysical Prospecting,2011,46(3):374-385

[7] 匡斌，王华忠，季玉新,等.任意复杂介质中主能量法地震波走时计算[J].地球物理学报,2005,48(2):390-394 Kuang B,Wang H Z,Ji Y X,et al.Main energy travel time calculation in arbitrary velocity distribution[J].Chinese Journal of Geophysics,2005,48(2):390-394

[8] Schneider W A,Ranzinger K A,Balch A H,et al.A dynamic programming approach to first arrival traveltime computation in media with arbitrarily distributed velocities[J].Geophysics,1992,57(1):39-50

[9] 段鹏飞,程玖兵,陈三平,等．TI介质局部角度域射线追踪与叠前深度偏移成像[J]．地球物理学报，2013，56(1)：269-279 Duan P F,Cheng J B,Chen S P,et al.Local angle-domain ray tracing and prestack depth migration in TI medium[J].Chinese Journal of Geophysics,2013,56(1):269-279

[10] 袁江华，刘洪，首皓,等.面向目标的叠前角度道集提取策略[J].石油物探,2007,46(4):334-338 Yuan J H,Liu H,Shou H,et al.Strategy for targeted prestack angle gather extract[J].Geophysical Prospecting for Petroleum,2007,46(4):334-338

[11] 王华忠，刘少勇，孔祥宁，等.大规模三维地震数据Kirchhoff叠前深度偏移及其并行实现[J]．石油地球物理勘探,2012,47(3):404-410 Wang H Z,Liu S Y,Kong X N,et al.Large-scale 3d seismic data Kirchhoff prestack depth migration and parallel reality[J].Oil Geophysical Prospecting,2012,47(3):404-410

[12] 宋翔宇,李振春,周卿，等.共散射点道集映射噪声压制方法及其应用[J].石油物探,2013,52(5):524-529 Song X Y,Li Z C,Zhou Q,et al.Mapping noise suppression in common scattering point gathers and its application[J].Geophysical Prospecting for Petroleum,2013,52(5):524-529

[13] Sun J G.On the limited aperture migration in two dimensions[J].Geophysics,1998,63(3):984-994

[14] Klokov A,Fomel S.Optimal migration aperture for conflicting dips[J].Expanded Abstracts of 82ndAnnual Internat SEG Mtg,2012,504-507

[15] Schleicher J,Hubral P,Tygel M.Minimum apertures and fresnel zones inmigration and demigration[J].Geophysics,1997,62(2):183-194

[16] Sun J G.Limited aperture migration[J].Geophysics,2000,65(2):584-595

[17] Audebert F,Nicoletis L，Froidevaux P.Regularization of illumination in angle domains-a key to true amplitude migration[J].The Leading Edge,2005,24(6):643-654

[18] Audebert F,Foridevaux P,Racotoarisoa H,et al.Insights into migration in the angle domain[J].Expanded Abstracts of 72ndAnnual Internat SEG Mtg,2002,1188-1191

(编辑：陈 杰)

The analysis of characteristics of reflection and diffraction wave in dip angle gathers and the method for enhancing the imaging quality

Xu Hui

(GeophysicalResearchInstitute,ShengliOilfield,Sinopec,Dongying257022,China)

The identification and evaluation of lithologic reservoir is very important for the exploration in Eastern China,which is mainly based on fidelity angle gathers.The quality of angle gathers and stack section is the foundation of the identification and evaluation of the lithologic reservoirs.As we know,the characteristics of reflection and diffraction from common opening angle and dip angle gathers are totally difficult.In this paper,we analyze the difference and relation between the reflection and diffraction wave in the opening angle and dip angle domain respectively.Then,we construct a filter by using the angle distribution in dip angle domain to improve the quality of imaging gathers.Because of the dip angle is consistent with the subsurface interface,this method can improve imaging quality and get the purpose of fidelity reflection characteristics.The numerical examples demonstrate the effectiveness of the proposed method.

opening angle gathers,dip angle gathers,dip filter,imaging quality

2014-11-29;改回日期：2015-01-22。

徐辉(1966—)，男，高级工程师，主要从事地震资料处理和技术研究工作。

中国石油化工股份有限公司科技部“非一致性时移地震深化研究及应用”项目(P13076)资助。

P631

A

1000-1441(2015)02-0133-09

10.3969/j.issn.1000-1441.2015.02.003