电网接入风力发电后电压薄弱区域的分析方法
徐 群,李文升,崔力勃,尹 志,赵 晶,宋敏平
(国网山东青岛供电公司经济技术研究所 山东青岛266002)
电网接入风力发电后电压薄弱区域的分析方法
徐 群,李文升,崔力勃,尹 志,赵 晶,宋敏平
(国网山东青岛供电公司经济技术研究所 山东青岛266002)
电网运行中的电压稳定事故往往由电压薄弱节点故障引起,进而蔓延至全网。风机接入电网后,其出力波动会导致节点电压薄弱程度发生变化,因此在分析电压薄弱区域时,需要考虑风机出力的波动性和不确定性。提出一种考虑风机出力波动性的电网电压薄弱区域分析方法,通过蒙特卡罗这种以概率统计理论为指导的数值计算方法,利用风速概率分布对风速抽样,应用风速-功率关系获得风机出力,计算风机不同出力下电网各节点的电压薄弱指标,并通过统计分析估计电网的薄弱区域及其薄弱程度。以东北某区域电网为例,对含风机电网中薄弱区域进行了估计,研究了风机容量对薄弱区域的影响和风机功率因数对系统电压稳定性的影响。
风机 出力波动 电压稳定 薄弱区域 LC值
0 引 言
随着对环境问题的关注和技术的日益进步,风力发电越来越得到重视,其在未来电网中的占比也会越来越大,因而风电接入电力系统产生的影响不可回避。风力发电是将风能转换成电能,因而其出力很大程度上受风速的影响,风速的波动会导致风机出力的波动,进而对电网产生影响。[1-4]
虽然风机接入对电网电压稳定性影响方面已有不少研究,但是考虑风机出力波动下的电网电压薄弱区域方面研究尚不充分。文献[5]使用模态分析法考察了风机几种不同出力下的电压薄弱节点变化情况。综上,目前的研究从反映系统电压稳定性的不同角度、不同指标,分析了风机接入对电压稳定的影响,均取得了一定的成果,但是对于风机出力特点的体现还不够充分,虽然有的研究考虑到了风机出力的波动,但并没有考虑风机出力的不确定性。采用基于奇异值分解法的 LC指标,求出不同出力下各节点的薄弱指标,进行综合统计估计系统电压薄弱区域,探讨影响薄弱区域薄弱程度的因素。[6-9]
1 基于奇异值分解的节点电压薄弱指标
为了对薄弱区域进行分析,需要采用合适的分析方法获取薄弱指标。[10-11]通过奇异值分解法获得的最小奇异值指标是电力系统中一种表征系统电压稳定性的指标,它数学理论严谨,计算简单,应用广泛。文献[12]在此基础上提出一种识别节点电压薄弱程度的LC指标,该指标准确、简洁、实用。
1.1 奇异值分解法概述
设A∈Rm×n,则存在单位正交矩阵U和V,使得:

式(1)中,称 δ1,δ2,…,δn,(δr+·1=δr+2=…=δn=0)为 A的奇异值,称U的列向量Ui为A的右奇异向量,V的列向量Vi为A的左奇异向量。
对线性方程组 AX=b,A∈Rm×n,A是非奇异的,而 b∈Rn。则对矩阵A进行奇异值分解后,方程的解可以表示为:

由式(2)可以看出,如果奇异值 δi足够小,则矩阵 A或向量 b的微小变化都会引起 X的很大变化。δmin是所有奇异值中最小的一个,因而可以用来反映雅克比矩阵接近奇异的程度。电力系统中也广泛用最小奇异值来表示系统整体的电压稳定性。
1.2 节点电压薄弱LC指标
假设一个电力系统,除去平衡节点外,系统的节点总数为n,m为电压可调的节点数,矩阵J为完全雅克比矩阵;子矩阵JPθ、JPQ、JQθ、JQU为潮流方程偏微分形成的雅克比矩阵的子阵,则系统的潮流方程的线性化形式为:

设Vi是左奇异向量,Ui是右奇异向量,若对矩阵J进行奇异值分析,可得到:

若其中一个奇异值接近 0,则系统接近崩溃,系统响应由最小奇异值 δ2n-m和它对应的奇异向量 U2n-m和 V2n-m所决定,可得:
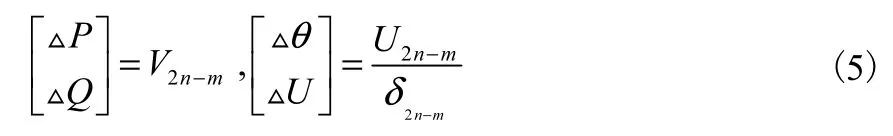
由上式可以看出,当系统接近于电压崩溃点时,最小奇异值非常小,很小的功率波动将可能引起电压很大的变化。U2n-m中最大的元素对应最灵敏的节点电压,因此,右奇异向量可以用于识别系统中的薄弱节点,可以定义节点薄弱程度指标:
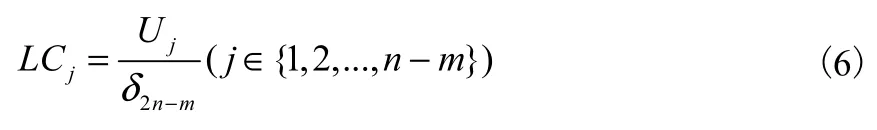
2 风机出力波动特性
为了正确估计含风机电网的电压薄弱区域,必须要考虑风机的出力波动性。风力发电是将风能转换成电能,而风速是决定风能大小的重要因素。Weibull分布是概率分布模型中最常用的模型,其在风速仿真中的有效性也得到了验证。[13]因此本文采用双参数的Weibull分布,其表达式如下:

式中,c是威布尔尺度因子,其单位与风速单位相同;k是无单位的威布尔形状因子;v是风速,vi是一个特定风速;dv是风速增量;P(v<vi<v+dv)是风速在v和v+dv之间的概率。
风速对风机出力的作用体现在风速-功率关系上。风机获取风能并转换为机械能传递给发电机,发电机再将机械能转换成电能供给电网,整个过程表达式如下:

式中,Pm为风机的机械功率(W);Cp为风能转换为机械能的利用系数;Pw为风机扇叶区域风能大小;PE为风机对外发出功率;A为叶片扫掠面积(m2);ρ为空气密度(kg/m3);vw为风速;η为机械能转换为电能的效率系数。
实际工作中风机在不同风速下有不同的动态特性,如图1所示。当风速低于切入风速或高于切除风速时,风机均不工作。额定功率是在额定风速下的功率。

图1 风机的风速-功率关系Fig.1 Relationship between wind speed and power of wind turbine
结合公式(8)、(9)和图1,可以得到风机风速-功率数量关系为:
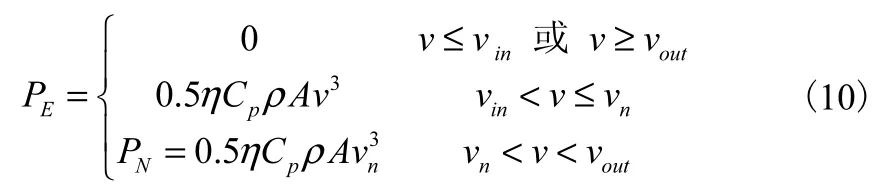
式中,vin为切入风速,vout为切出风速,vn为额定风速,PN为额定功率。
公式(7)描述了风速的分布规律,而公式(10)描述了不同风速对应的风机出力。因此风速自身的波动使得风机出力也具有波动性。
3 含风机电网的薄弱区域分析方法
蒙特卡罗法在电力系统中也得到广泛应用。由于风速具有特定的概率分布,因而采用蒙特卡罗法,可以较好的模拟实际风速的变动,进而利用风速-功率关系获得风机实际运行出力变动,针对实际运行可能出现的各种系统状态,进行相应的分析。[15]
将蒙特卡罗算法与电网电压薄弱区域分析结合,考虑风机出力波动下的电网电压薄弱区域分析,可以克服传统分析方法中仅采用几种给定风机出力,使得对出力波动性考虑不够全面和忽视出力不确定概率的缺陷,可以实现更加科学合理的分析效果。本文所设计的考虑风机出力波动的电网薄弱区域分析流程如图2所示。
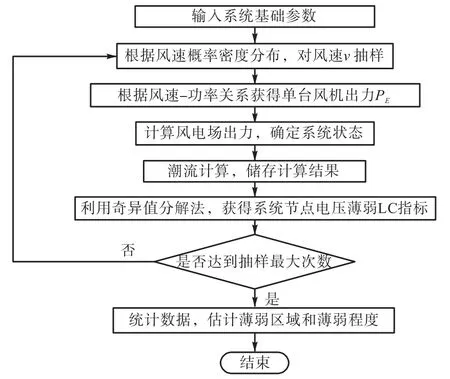
图2 程序流程图Fig.2 Flow chart of the program
程序的基本步骤为:①输入基本系统参数。包括风速参数、系统结构、风电场容量、风机节点类型等。②利用计算机产生的伪随机数,根据风速的概率分布,随机抽样确定系统中风速的大小。③利用风速-功率关系确定风机出力。再根据风机出力和风电厂容量获得风电场出力,确定系统状态。④进行潮流计算,获得系统各个参数和雅克比矩阵。⑤对雅克比矩阵进行奇异值分解,获得节点电压薄弱指标(LC值)。⑥重复步骤②~⑤直到达到设定的仿真次数。⑦对结果进行统计分析,进行电压薄弱区域分析。
在统计分析中,针对仿真所得的不同风机出力下的雅克比矩阵最小奇异值的平均值代表系统电压稳定程度,节点 LC指标的平均值代表节点薄弱程度,并采用区域最薄弱节点的LC指标来表示区域的薄弱程度。
4 算例分析
4.1 仿真系统接线图
为了验证所提出方法的有效性,以我国华北某区域电网为例进行仿真分析,接线图如图3所示。该系统中有 48个节点,52条线路,17台变压器,电压等级为220,kV和66, kV,总负荷为1,456.7 MW。系统共有15个风电场,风机采用恒功率因数控制方式,风机总装机容量为210.12 MW,有6台火力发电机组,5号节点为无穷大系统。风机相关参数如下:威布尔参数c=15 m/s,k=2,切入风速为4 m/s,切出风速为25 m/s,额定风速为13 m/s,空气密度为1.2 kg/m3,考虑到风电场处于同一区域,为了简化,忽视风速的时移效应和风电场内部的尾流效应,风速统一为一个值。
根据实际地理位置和接线情况可将系统划分为多个区域:其中包含风机的区域为:I{7,8,9,10,11,12,13};II{23,40,44,45,46,47};III:{25,36,37,38,39};IV{2,19,20,21};V:{27,41,42};VI:{29,43}。这些区域与系统其他部分都是仅通过一条线路联系。

图3 地区电网模型Fig.3 Model of regional grid
4.2 算例1——薄弱区域估计
风机功率因数设定为 1,仿真次数为 4,000。按仿真所得LC值的平均值大小对节点进行排序,从大到小(即从最薄弱区域开始)。为了简便起见,本文仅考虑前10个节点。前10节点薄弱程度数据统计结果如表1所示。
从结果可以看出:①前 10个薄弱节点均来自含有风机且与外部联系不紧密的区域。②最薄弱节点为 Bus12,薄弱区域薄弱程度I>III>II。
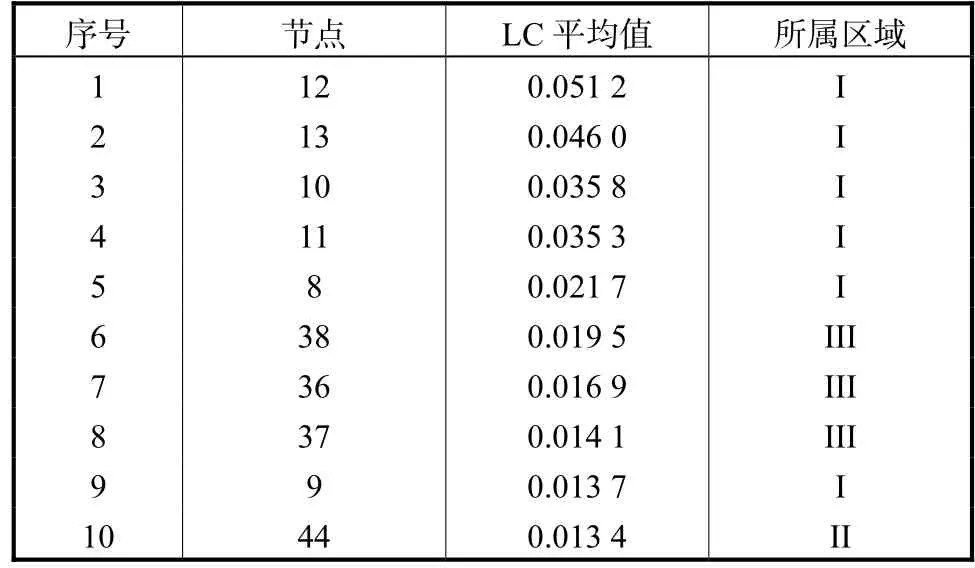
表1 节点LC值统计结果Tab.1 Statistical result of nodes’ LC values
所以,当某区域负荷供电主要通过风机提供,区域与外界联系又不强的时候,该地区很容易成为电压薄弱区域。主要原因是风机的波动性使得负荷供电并不稳定,而由于区域和外部电网联系不紧密,很难获得足够的功率来支持负荷,所以导致该区域容易出现电压崩溃现象。
4.3 算例2——风电场容量变化对薄弱区域影响
算例 1中的风机总的装机容量为 210.12 MW,占负荷的14.42%,,在本算例中逐渐增加风机的装机容量,考察其增加到2倍、3倍、4倍情况下,系统薄弱区域变化的特点。不同风机装机容量下的薄弱节点排序如表 2所示。最小奇异值平均值和Bus12的LC平均值随容量的变化如图4所示。

表2 风机容量变化下前8个薄弱节点Tab.2 Data of the former 8 weak nodes
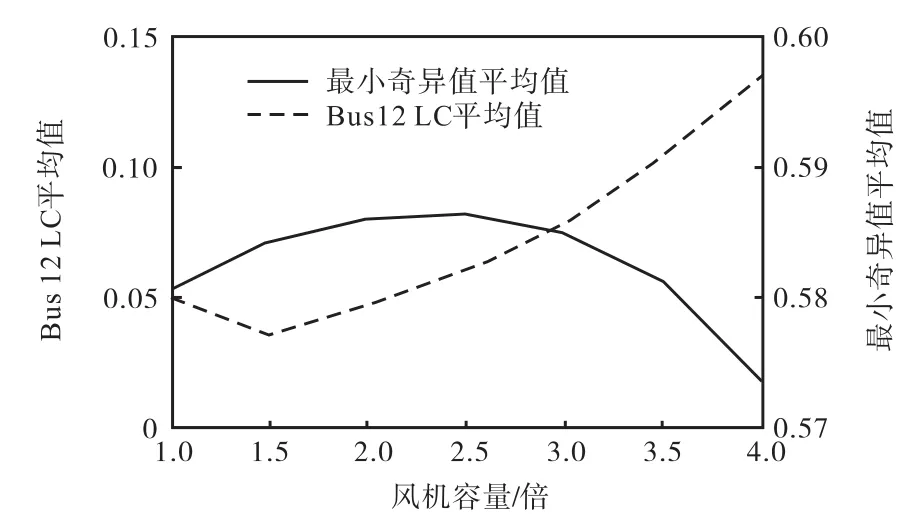
图4 不同风机容量最小奇异值平均值和Bus12 LC值平均值Fig.4 Average minimum singular values and Bus12 LC average values
从表2、图4中可以看出:①最薄弱区域并未发生改变,仍然是 I区域。②随着风机容量发生变化,薄弱排序发生变化。随着风机容量增加,Ⅱ区域取代Ⅲ区域成为次薄弱区域。③随着风机容量逐渐增加,薄弱区域薄弱程度呈现先减少再增大的趋势。④随着风机容量逐渐增加,整个电网电压稳定性呈现先增大再减小的趋势。
所以,风机容量的变化对于薄弱区域的变化有一定的影响。存在一个最优的容量使得整个电网的稳定性最好,也存在一个最优容量使得该风机容量下全网的最薄弱区域薄弱程度相对最低。
4.4 算例3——风机功率因数对系统电压稳定性影响
算例1中风电场的输出功率因数为1,即风电场对外不发出无功也不消耗无功。实际运行,风电场的功率因数是在一定允许范围内的,可以向电网发出或从电网吸收一定的无功功率。一般情况下,要求的功率因数范围从超前 0.9到滞后0.9,本文对超前功率因数 0.9到滞后功率因数 0.9之间的区间选取了 11个功率因数值,考察不同功率因数下的系统电压稳定性变化,如图5所示。
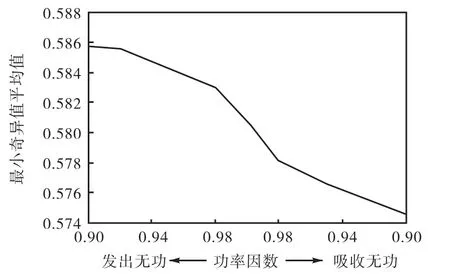
图5 不同功率因数下的系统电压稳定性Fig.5 System voltage stability under different power factors
可以看出:功率因数的变化会影响系统的电压稳定性,风电场发出感性无功越多,整个系统的电压稳定性越好。
5 结 语
本文提出了一种考虑风机波动性的含风机电网电压薄弱区域研究的方法,利用蒙特卡罗法多次仿真以获得不同风机出力下的电压状态,对相应状态分析获得节点薄弱指标,最终统计分析寻找电压薄弱区域和薄弱区域的薄弱程度。应用于某地区含风机电网的算例仿真表明:①当区域内负荷主要由风机供电而区域对外连接不紧密时,该区域容易成为电压薄弱区域。②存在一个最优风机容量使得全网的最薄弱区域薄弱程度与其他风机容量下的该区域薄弱程度相比最低。③功率因数变化会影响系统的电压稳定性,风电场发出感性无功功率越多,则电力系统整体的稳定性越大。■
[1] 李剑楠,乔颖,鲁宗相,等. 大规模风电多尺度出力波动性的统计建模研究[J]. 电力系统保护与控制,2012,40(19):7-13.
[2] 孙涛,王伟胜,戴慧珠,等. 风力发电引起的电压波动和闪变[J]. 电网技术,2003,27(12):62-66,70.
[3] 范国英,董存,郭雷,等. 吉林省风电机组大规模并网相关问题分析[J]. 吉林电力,2008,36(3):1-3,8.
[4] 林莉,孙才新,王永平,等. 大容量风电场接入后电网电压稳定性的计算分析与控制策略[J]. 电网技术,2008,32(3):41-46.
[5] 陈海焱,段献忠,陈金富. 分布式发电对配网静态电压稳定性的影响[J]. 电网技术,2006,30(19):27-30.
[6] 陈宁,朱凌志,王伟. 改善接入地区电压稳定性的风电场无功控制策略[J]. 中国电机工程学报,2009,29(10):102-108.
[7] 朱翰超. 风电波动对电网稳定性影响及无功电压控制策略研究[D]. 北京:华北电力大学,2013.
[8] 李兴源,王秀英. 基于静态等值和奇异值分解的快速电压稳定性分析方法[J]. 中国电机工程学报,2003,23(4):5-8,24.
[9] Nam H K,Kim Y K. A new eigen-sensitivity theory of augmented matrix and its applications to power system stability analysis[J]. IEEE Transactions on Power System,2000,15(1):363-369.
[10] 熊虎,李雪凌,彭志炜. 电力系统电压薄弱点的快速寻求发[J]. 贵州工业大学学报(自然科学版),2007,36(6):44-47,55.
[11] 吴华坚,李兴源,贺洋,等. 考虑负荷静特性的基于奇异值分解法静态电压稳定分析[J]. 四川电力技术,2009,32(3):5-8,13.
[12] 丁明,吴义纯,张立军. 风电场风速概率分布参数计算方法的研究[J]. 中国电机工程学报,2005,25(10):107-110.
[13] 吴义纯,丁明. 基于蒙特卡罗仿真的风力发电系统可靠性评价[J]. 电力自动化设备,2004,24(12):70-73.
[14] 张瑞华,宋云亭. 基于蒙特卡罗仿真和电压安全约束的无功优化算法[J]. 电力系统自动化,2002,26(7):23-27.
An Analysis Method of Voltage Weak Area of Power Grid Wind Power Integration
XU Qun,LI Wensheng,CUI Libo,YIN Zhi,ZHAO Jing,SONG Minping
(Institute of Economic Technology,Shandong Qingdao Power Supply Company of State Grid,Qingdao 266002,Shandong Province,China)
Voltage stability related accidents of power grid are often caused by faults of voltage weak nodes,which continue to spread to the whole grid. When wind power is connected to the grid,the weak degree will be affected by fluctuations of wind farms’ outputs. Thus it is necessary to consider the fluctuation when analyzing a grid’s voltage weak areas. This paper proposes a method of analyzing voltage weak areas of grid considering the fluctuation of wind farms’ output. Using Monte Carlo method,wind speed was sampled with its probability distribution and wind farms’ output was obtained with the relation between wind speed and wind farms’ output,then voltage weak degrees of nodes were calculated. Through statistical analysis,weak areas of wind power connected grid were estimated. Taking a regional gird in northeastern China for example,voltage areas were estimated. The effect of wind farms’ capacity on weak areas and power factor on system voltage stability were also studied.
wind power;output fluctuation;voltage stability;weak area;LC value
TM315
A
1006-8945(2015)07-0031-04
2015-06-05

