“鸡兔同笼”的解法

杨洋

“鸡兔同笼”是我国古代著名的趣题之一。解决“鸡兔同笼”问题，通常采用列表法和假设法。采用假设法，可以假设都是鸡，那么兔的只数=（脚的总数-鸡兔总数€酌恐患Φ慕攀﹢鳎恐煌玫慕攀恐患Φ慕攀Φ闹皇？鸡兔总数-兔的只数；也可以假设都是兔，则鸡的只数=（鸡兔总数€酌恐煌玫慕攀诺淖苁﹢鳎恐煌玫慕攀恐患Φ慕攀？

【题目】鸡兔共有40只，鸡和兔的脚共有112只。鸡和兔各有多少只？

【分析与解】这是一道基本的“鸡兔同笼”问题，有多种解法。

解法一 假设法。假设都是鸡，那么一共有脚40€？=80（只），比实际少112-80=32（只）。用一只兔去换一只鸡，可以增加（4-2）只脚；要增加32只脚，需要用32€鳎？-2）=16（只）兔去换鸡。所以，兔有16只，鸡有40-16=24（只）。

假设都是兔，那么一共有脚40€？=160（只），比实际多160-112=48（只）。用一只鸡去换一只兔，可以减少（4-2）只脚，所以鸡有48€鳎？-2）=24（只），兔有40-24=16（只）。

小提醒：假设都是鸡，先算出的是兔；假设都是兔，则先算出的是鸡。

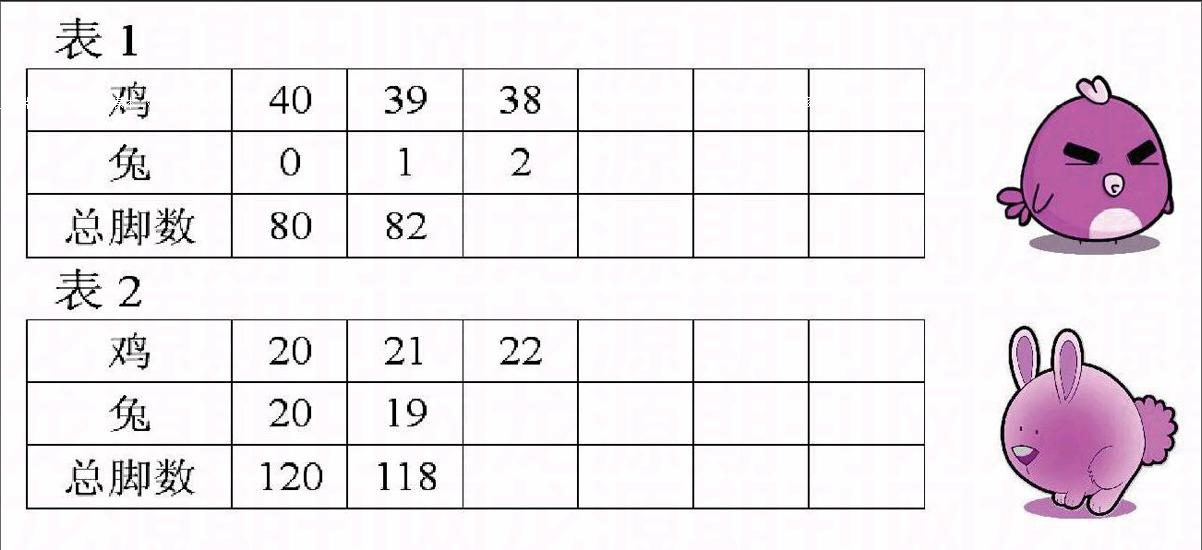
解法二 列表法。如果鸡兔总数较少，可以列如下表1找答案；像本题鸡兔总数较多，可以从鸡兔各占一半算起。如下表2，鸡、兔各有20只，共有脚120只，比实际112只略多，所以应增加鸡减少兔。你能接着填表找出答案吗？

解法三 “除减”法。如果每只鸡都是“金鸡独立”，一只脚站着；每只兔像人一样用两只脚站着，那么落地的脚数还有112€？=56（只）。这时每只鸡一只脚，每只兔两只脚。只要兔多一只，脚的总数就比头的总数多1，所以兔有56-40=16（只），鸡有40-16=24（只）。这种算法，只做一次除法和一次减法就能算出兔子的只数了，很简单。但如果“脚数”不是4和2（如：三轮摩托车和四轮小汽车的“脚数”分别是3和4），就不能用这种算法了。

聪明的小读者，“鸡兔同笼”问题的解法你学会了吗？下面请你来露一手吧！

1.养殖场里养了猪和鹅共27只，一共有86条腿。养殖场养了（ ）头猪，（ ）只鹅。

2.一次数学竞endprint