基于抵偿面方法的局部坐标系的建立
杨立光
(四川省清源工程咨询有限公司,四川成都 610072)
基于抵偿面方法的局部坐标系的建立
杨立光
(四川省清源工程咨询有限公司,四川成都 610072)
如何实现WGS-84地心空间直角坐标与地方独立坐标间的转换,特别是如何减小投影变形一直是工程师们所关注的热点问题。文章以焦作市为例,采用选择抵偿面的方法建立局部坐标系,对此问题进行探讨。
大地测量; 坐标系; 投影变形; 抵偿面
《城市测量规范》与《工程测量规范》中明确规定:平面控制网的坐标系统,应满足测区内投影长度变形值不大2.5 cm/km。如果投影长度变形值在此范围内,则可以采用统一的高斯正形投影3°带平面直角坐标系统。大于此要求时,则必须选择适宜的投影坐标系统,以抵偿或削弱长度变形的影响。
本文以焦作市为例,通过对参考椭球、高斯—克吕格投影及平面坐标和空间坐标的相互转换等一系列基本理论的阐述,分析研究参考椭球、投影参数的变化对地面点高斯坐标的影响,以便为城市测量工作提供一些参考意见。
1 焦作市在国家投影带中精度方面存在的问题
1.1 焦作市的地理概况
焦作市位于北纬34°与36°之间,经度位于112°与114°之间。它包括沁阳、孟州市、温县、修武和武陟几个县。高程逐渐分布,东部最低达85 m,西部最高达153 m,东西长约70 km,南北长约50 km。
1.2 焦作市采用国家3°投影带精度方面存在的问题
焦作市东西长度较长,因此最好采用变换投影带的方法,即以国家3°带经度114°为中央子午线的经度。以114°经度为纵轴即x轴,与其相垂直的纬线为横轴即y轴,则离中央子午线越远的边投影后变形越大(其中最西部即孟州市西边界的变形最大)。
投影长度变形是指将地面观测值先归算到参考椭球面(或大地水准面)上,然后再从参考椭球面归化到高斯平面上,在变换过程中,长度发生了明显变形,其大小按下面公式计算。
(1)地面长度投影到参考椭球面 (高程归化改正)
(1)
(2)参考椭球面上边长归化至高斯平面上 (高斯投影变形)
(2)
(3)投影长度变形
Δs1+Δs2=Δs
(3)
式中:Hm为归算边高出参考椭球面的平均高程;s0为投影归算边长;ym为归算边两端点横坐标平均值;s为归算边的长度 ;R为地面边方向参考椭球面法截弧曲率半径;Rm为参考椭球面在地面边中点的平均曲率半径,近似取R,Rm为6 371 km。
将上述数据代入公式可得相对精度:
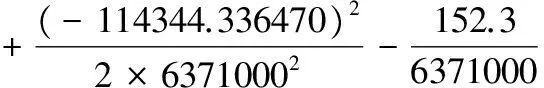
因为13.7153 cm/km远大于2.5 cm/km,所以需重新选择新的投影带。
2 采取选择抵偿面的方法进行精度的提高
下面以焦作市为例采取选择抵偿面的方法进行精度的提高。抵偿原则:选择“抵偿高程面”作为投影面,按高斯正形投影3°带计算平面直角坐标。由上面提到的公式可知:将距离由较高的高程面算至较低的高程面时,长度总是减小的;而将椭球面上的距离化算至高斯平面时,长度总是增加的。所以两个投影过程对长度变形具有抵偿的性质。如果选择适当的椭球半径,使距离化算到这个椭球面上所减小的数值,恰好等于这个椭球面化算至高斯平面所增加的数值,那么高斯平面上的距离同实地距离就一致了。这个适当的椭球面就称为“抵偿高程面”。
即令
ΔS1+ΔS2=0
则代入数据得:
式中:y以100 km做单位;Hm以m做单位。
该地的平均高程为110.375 m,抵偿面应比平均高程面低1 026.358 m。所以抵偿面的高程为110.375+1026.358=1136.733 m。
这时,再次计算最远边的长度变形精度:
将最远点即孟州县西边缘的点换算到抵偿高程面相应的坐标系中去,其原坐标为(3856817.397713,385655.663530)
取一个国家的大地点作远点,例如点B=34°50′00″,L=113°00′00″其转化为直角坐标为(856560.872117,408525.246367)且保持它在3°带国家统一坐标值不变,而将最远点即孟州县西边缘的点换算到抵偿高程面相应的坐标系中去,换算公式为:
式中:R为该地平均纬度处的椭球平均曲率半径;Hd为抵偿高程;xd、yd为原坐标点换算到抵偿高程面相应的坐标系的坐标值。
代入数据得:
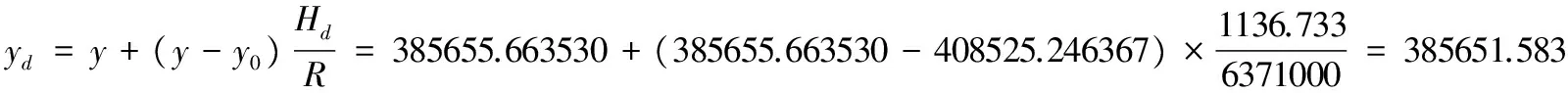
所以y的自然值为:
385651.583-500000=-114348.417 m
则相对精度为:
其值远远小于规定的精度,因而适用于各种用途。
3 结束语
高斯投影分带是限制长度变形的有效途径,而正确的选择控制网的坐标系统,则是抵偿长度综合变形的有效途径。本文所用方法是通过变更投影面来抵偿长度综合变形的,具有换算简便、概念直观等优点,而且换系后的新坐标与原国家统一坐标系坐标十分接近,有利于测区内外之间的联系。由于测区地形的不同,建立局部坐标系适用的方法也不尽相同,随着科技的进步,会有越来越多的方法建立具有高精度的局部坐标系。
[1] 武汉测绘科技大学.测量学[M].北京:测绘出版社,2003.
[2] 张凤举,张华海,赵长胜.控制测量学[M].北京:煤炭工业出版社,1999.
[3] GB 50026-2007 工程测量规范[S].
[4] CJJ/T8-2011城市测量规范[S].
P128.1
B
[定稿日期]2015-03-17

