基于强事件约束的微地震剩余静校正量估算方法

程磊磊,姜宇东,崔树果,郭全仕

(中国石油化工股份有限公司石油物探技术研究院,江苏南京211103)

基于强事件约束的微地震剩余静校正量估算方法

程磊磊,姜宇东,崔树果,郭全仕

(中国石油化工股份有限公司石油物探技术研究院,江苏南京211103)

针对低信噪比条件下微地震剩余静校正量估算困难的问题,研究了射孔事件数据道间的两两相关信息与强微地震事件同相轴光滑性约束条件相结合的微地震剩余静校正量估算方法。该方法不仅利用了射孔事件的任意两道相关信息,增加微地震剩余静校正量估算时的信息量;还利用了剩余静校正后强微地震事件同相轴的光滑性约束信息,实现提高低信噪比条件下剩余静校正量估算精度的目的。模型资料和实际资料的测试结果表明,该方法对低信噪比数据的剩余静校正估算具有适应性强、效果好的特点。

微地震;低信噪比;剩余静校正;光滑约束条件

微地震监测技术是20世纪90年代发展和活跃起来的一项非常规技术,应用于评价水力压裂效果、矿产监测和地质灾害监测等诸多领域[1-2]。微地震监测效果取决于微地震事件的定位精度,而后者则依赖于微地震事件走时的精度、速度模型的精度和定位算法等[3]。剩余静校正量的存在直接影响微地震事件走时精度,进而影响微地震事件的定位精度[4-6]。因此,估算剩余静校正量是微地震资料处理中的重要步骤之一。

剩余静校正量估算常常会利用射孔事件。射孔事件是射孔弹在已知位置激发产生由微地震数据采集系统接收到的地震信号。从理论上来说,由于射孔位置已知,经过动校正和静校正处理后的射孔事件同相轴可完全拉平[7]。但通常情况下,处理后的射孔事件同相轴还可能存在局部抖动,即存在“剩余静校正量”。

针对剩余静校正问题,学者们开展过诸多研究[8-12]。地震数据信噪比足够高时,通过计算参考道和射孔事件数据道的互相关函数能有效地估算剩余静校正量[8];但对于信噪比低、能量弱的数据道,“相关法”不能有效地估算剩余静校正量。Aster等[13]和Rowe等[14]提出了一种利用数据道间的两两相关建立反演方程估算剩余校正量的方法,这里简称该方法为“两两相关法”。相比于仅仅和参考道求相关量,“两两相关法”利用数据道任意两道间的相关,获得了更多信息量,使得剩余静校正量的估算更稳健。但是,当信号的信噪比很低时,由于相关量估算误差增大,“两两相关法”估算剩余静校正量的能力也将下降。因此，采用多信息约束对反演算法的稳定性至关重要[15-16]。准确的剩余静校正不仅能消除射孔事件同相轴的局部扰动,使得同相轴变得光滑,也能够使该射孔段的压裂微地震事件的同相轴足够光滑。因此,剩余静校正后强微地震事件同相轴的光滑性是非常有用的反演约束信息。

本文研究了低信噪比条件下微地震剩余静校正量估算问题。在“两两相关法”的基础上,通过引入强微地震事件同相轴光滑性约束条件进行微地震剩余静校正量估算,达到提高低信噪比条件下剩余静校正量的估算精度的目的。

1 方法原理

1.1 两两相关法基本原理

这里剩余静校正量估算以经过动校正和静校正处理后的射孔事件为基础。对于经过处理后的N道射孔数据,可以通过互相关函数计算任意两道数据之间的事件延迟量。选取其中任意两道数据(如第i道和第j道),为了求取剩余静校正量,可建立如下方程:

(1)

式中:Δmi,Δmj分别为第i道和第j道的剩余静校正量;dij为这两道数据间的相关延迟量;σij为延迟量的方差。微地震数据普遍噪声干扰强、信噪比低,延迟量的估算可以采用相似滤波后再相关的方式实现[14]。

N道数据中任意两道,均可建立类似公式(1)的方程,组成如下矩阵方程:

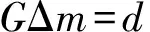
(2)

其中,

(3)

Δm=[Δm1,Δm2,…,Δmn]T

(4)

(5)

矩阵G的规模为[N(N-1)/2]·N,该矩阵是稀疏矩阵,每行仅有两个非零元素。当N很大时,矩阵G会变得更大;再则,该大型矩阵处理的是局部不光滑数据,可能难以得到稳定的效果。此时,可将N道数据分为若干个小道集(如,每个道集由10～20道数据组成)从而降低单个矩阵规模,有利于局部不光滑问题的求解。

求解方程(2)就能够估算出这N道的剩余静校正量,这就是“两两相关法”的基本思路[13-14]。数据的信噪比很低时,由于延迟量估算误差的增大,将会影响“两两相关法”的剩余静校正量估算,数据测试部分将说明这一点。

1.2 微地震事件的同相轴光滑性

准确的剩余静校正不仅能使处理后的射孔事件同相轴拉平,还能使得该射孔段的微地震事件的同相轴光滑。剩余静校正后强微地震事件同相轴的光滑性将是有效的反演约束信息。

这里利用微地震事件同相轴的“粗糙度”来反映同相轴的光滑性。粗糙度越低,则同相轴越光滑。粗糙度ri可以用剩余静校正后微地震事件相邻数据道间延迟量的局部二阶偏导数来表示:

(6)

公式(6)可以表示为矩阵形式:

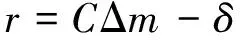
(7)

其中,

(8)

(9)

(10)

图1 剩余静校正前局部3道数据示意

1.3 基于强事件约束的剩余静校正方法

加入约束条件是提高反演方法稳定性的有效途径。剩余静校正后强微地震事件同相轴的光滑性是有效的反演约束信息。我们将剩余静校正后强微地震事件同相轴光滑性约束条件和“两两相关法”相结合,以达到提高剩余静校正估算的精度和稳定性的目的。

强微地震事件同相轴的光滑性要求其总粗糙度最小化。利用拉格朗日乘子法,加入光滑约束后目标泛函可表示为:

(11)

式中:λ为拉格朗日算子。

要求∂Φ/∂Δm=0,得到方程(11)的解为:

(12)

方程(12)也等效为如下线性方程的最小二乘解:

(13)

方程(13)就是本文方法的基本方程。求解(13)式即可得到每道数据的剩余静校正量。(13)式的求解可以采用奇异值分解(SVD)方法或者最小二乘共轭梯度法(LSCG)[17]。

2 模型数据测试

为了验证方法的有效性,先利用模拟数据进行验证。模拟数据为经动校正和静校正处理后的一个射孔事件和该射孔段压裂时产生的一个强微地震事件;每个数据共200道,子波为Ricker子波,主频50Hz(图2);在数据中加入高斯随机噪声,信噪比为5。从图2可以看出,射孔事件和微地震事件同相轴抖动严重,存在剩余静校正量。

下面对相关法、两两相关法和本文方法的处理效果进行对比分析。图3,图4和图5分别为这3种方法的处理结果。这3种方法剩余静校正后,射孔事件同相轴都被拉平,且微地震事件同相轴光滑,说明在信噪比足够高时,这3种方法均能有效地估算剩余静校正量。

当射孔数据信噪比降低至2时(图6),3种方法对应的剩余静校正处理结果如图7,图8和图9所示。从图7可以看出,由于射孔信号的信噪比低,相关法看似将射孔事件同相轴拉平,但剩余静校正量作用于微地震事件时,事件同相轴并不光滑(图7b),说明该剩余静校正量不完全正确;相比于相关法,两两相关法的效果有一定提高(图8b),但是,同相轴仍然存在少量不光滑(“毛刺”)现象。图9 为本文方法处理结果。对比图7,图8和图9可以看出,本文方法处理效果最佳,经剩余静校正后同相轴形态最好且最光滑。

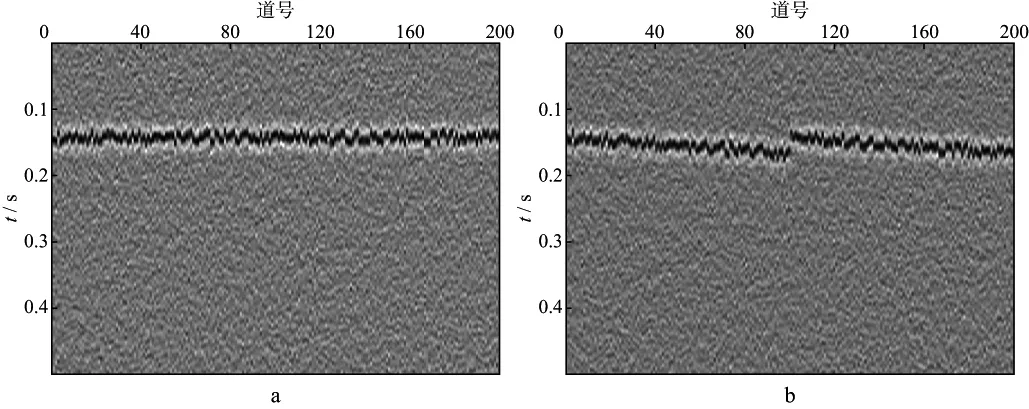
图2 模拟数据(射孔数据信噪比为5)

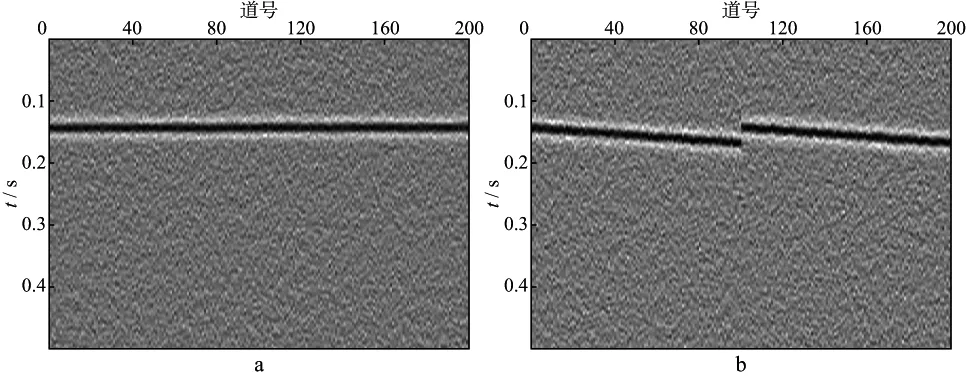
图4 两两相关法剩余静校正处理结果(射孔数据信噪比为5)

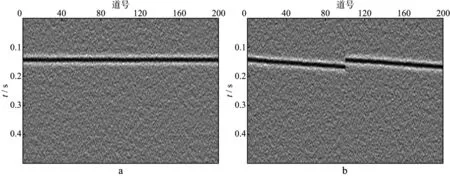
图5 本文方法剩余静校正处理结果(射孔数据信噪比为5)

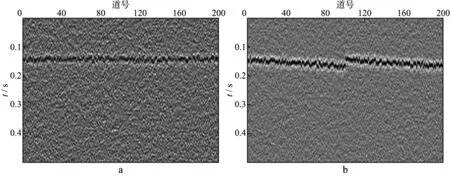
图6 模拟数据(射孔数据信噪比为2)

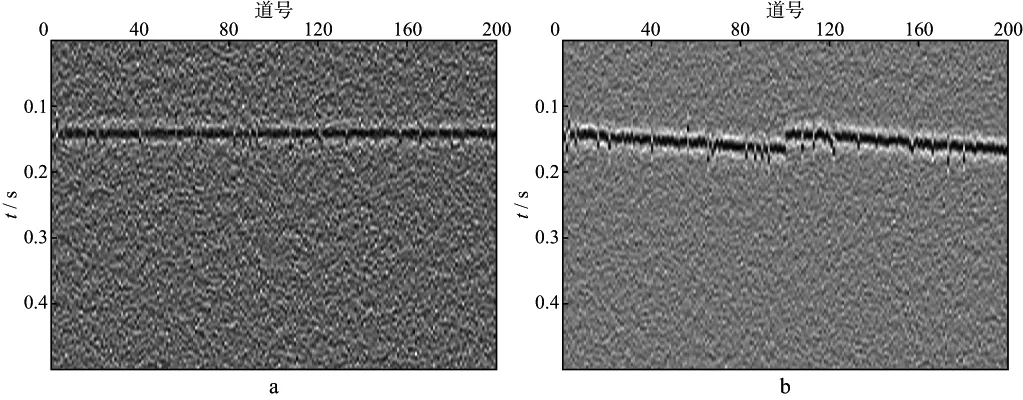
图7 相关法剩余静校正处理结果(射孔数据信噪比为2)

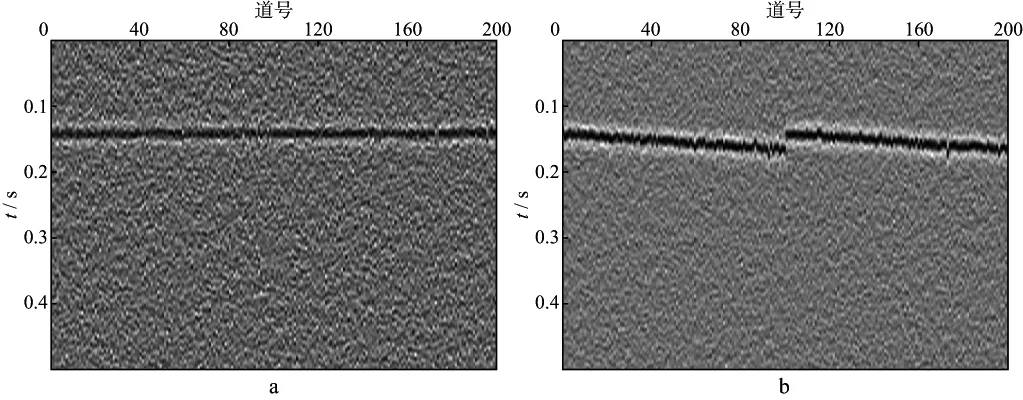
图8 两两相关法剩余静校正处理结果(射孔数据信噪比为2)

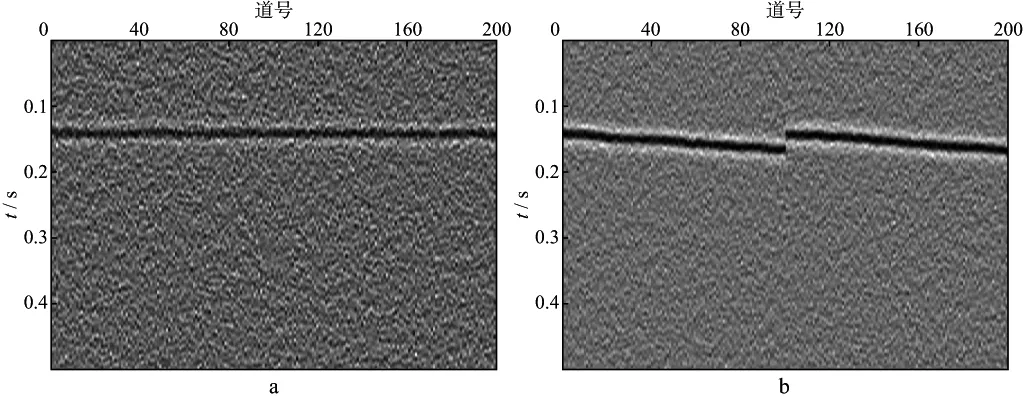
图9 本文方法剩余静校正处理结果(射孔数据信噪比为2)

当射孔数据信噪比进一步降为1时(图10),3种方法对应的剩余静校正处理结果如图11,图12和图13所示。从图11,图12和图13可以看出,随着信噪比的进一步降低,相关法剩余静校正后,微地震事件同相轴更加粗糙,甚至差于剩余静校正前原始数据(图11b);两两相关法剩余静校正后同相轴也比原始数据差(图12b);然而,本文方法依然有效,尽管剩余静校正量存在一定误差,但微地震事件同相轴依然连续和光滑(图13b)。模型数据测试结果说明低信噪比数据时本文方法处理效果更好。

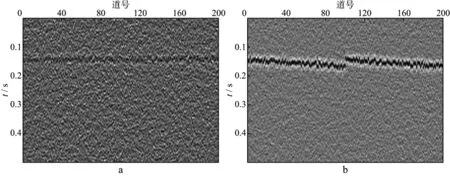
图10 模拟数据(射孔数据信噪比为1)

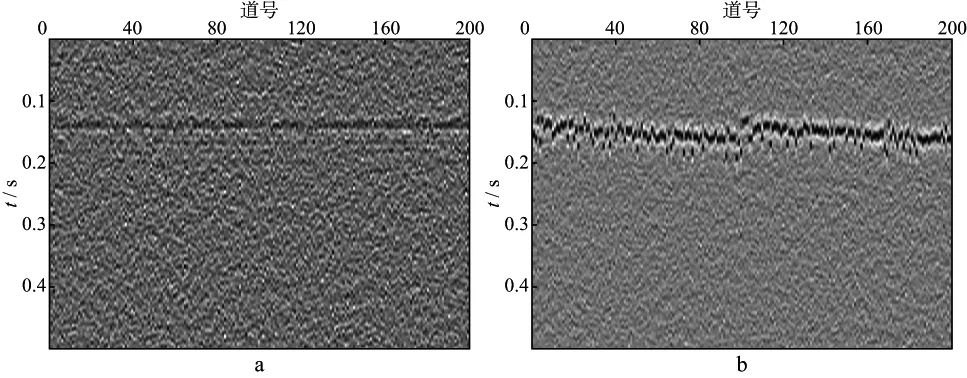
图11 相关法剩余静校正处理结果(射孔数据信噪比为1)

图12 两两相关法剩余静校正处理结果(射孔数据信噪比为1)

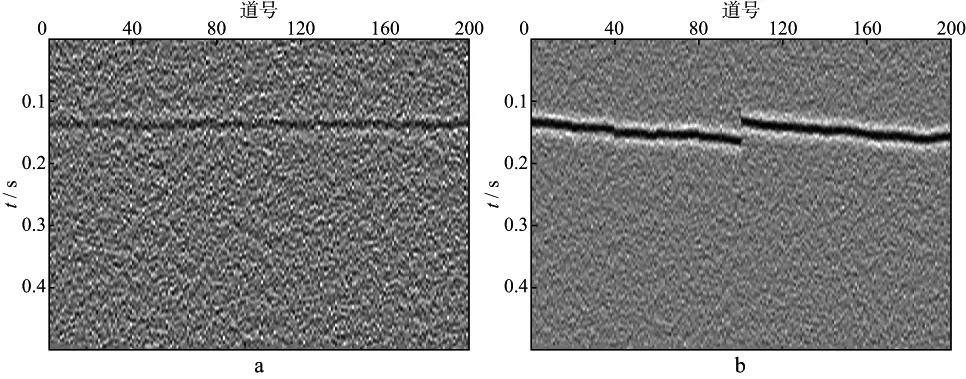
图13 本文方法剩余静校正处理结果(射孔数据信噪比为1)

3 实际数据测试

利用某实际地面微地震资料来验证本文方法的效果。图14a和图14b为经过动校正和静校正处理后的某实际射孔事件和该射孔压裂段的一个强微地震事件(部分数据,80道),可以看出,射孔事件同相轴没有完全拉平,存在剩余静校正量(图14 中蓝框部分);图15为相关法剩余静校正处理后的结果,由于射孔数据部分道的信噪比很低,剩余静校正后微地震事件同相轴(40～80道)并不连续(图15b中红圈部分);图16为两两相关法剩余静校正处理后的结果,两两相关法在该数据中低信噪比道的处理结果也不理想(图16b中红圈部分);图17为本文方法处理后的结果,图17b中红圈部分所示剩余静校正后同相轴形态连续。综上所述,在信噪比高时,3种方法都能有效解决静校正问题;但当射孔信号信噪比很低时,相关法和两两相关法处理效果不佳,本文方法则取得较好的处理效果。

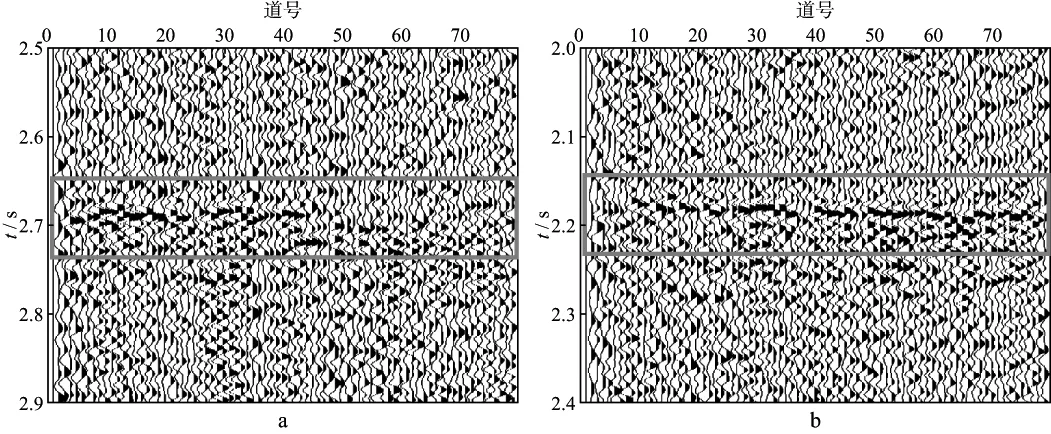
图14 某实际地面微地震数据(部分数据,80道)

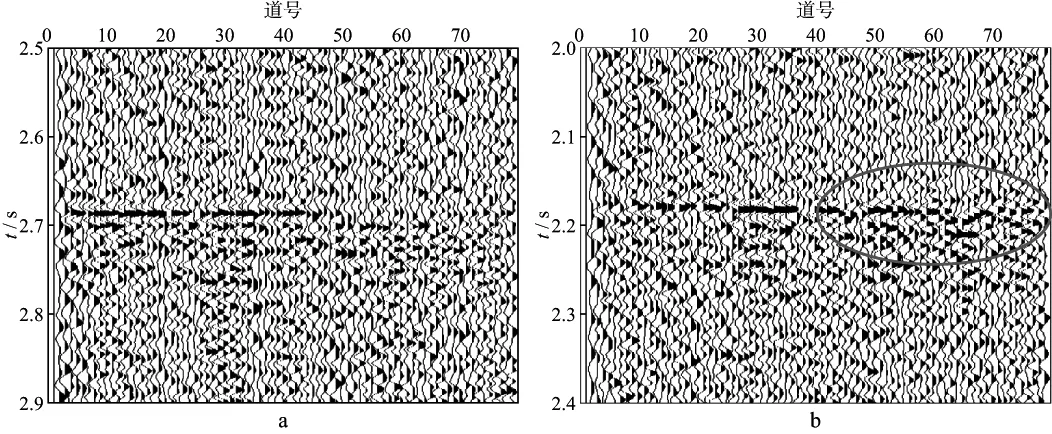
图15 相关法剩余静校正处理结果

图16 两两相关法剩余静校正处理结果

图17 本文方法剩余静校正处理结果

4 结束语

微地震剩余静校正对微地震事件的定位精度、弱事件识别等有较大影响,是微地震资料前期处理中的关键环节之一,在低信噪比资料中尤为如此。微地震资料通常噪声干扰多、能量弱、信噪比低,常规相关法剩余静校正方法对这种资料的处理效果不理想。本文提出的基于强微地震事件光滑性约束的剩余静校正估算方法,利用强事件同相轴光滑性作为约束条件能有效提高低信噪比数据的剩余静校正量的估算精度。模型资料和实际资料的测试结果表明,在低信噪比射孔数据条件下,该光滑性约束剩余静校正方法的运算更稳定、效果更好,是一种有效的低信噪比微地震数据剩余静校正估算方法。

[1] Duncan P M,Eisner L.Reservoir characterization using surface microseismic monitoring[J].Geophysics,2010,75(5):75A139-75A146

[2] Maxwell S C,Rutledge J,Jones R,et al.Petroleum reservoir characterization using downhole microseismic monitoring[J].Geophysics,2010,75(5):75A129-75A137

[3] Pavlis G L.Appraising earthquake hypocenter location errors:a complete,practical approach for single-event locations[J].Bulletin of the Seismological Society of America,1986,76(6):1699-1717

[4] Gomberg J S,Shedlock K M,Roecker S W.The effect of S-wave arrival times on the accuracy of hypocenter estimation[J].Bulletin of the Seismological Society of America,1990,80(6):1605-1628

[5] Schaff D P,Bokelmann G H R,Ellsworth W L,et al.Optimizing correlation techniques for improved earthquake location[J].Bulletin of the Seismological Society of America,2004,94(2):705-721

[6] Diehl T,Kissling E,Husen S,et al.Consistent phase picking for regional tomography models:application to the greater Alpine region[J].Geophysical Journal International,2009,176(2):542-554

[7] 姜宇东,宋维琪,郭晓中,等．地面微地震监测资料静校正方法研究[J]．石油物探,2013,52(2):136-140 Jiang Y D,Song W Q,Guo X Z,et al.Static correction method for surface microseismic monitoring data[J].Geophysical Prospecting for Petroleum,2013,52(2):136-140

[8] Schaff D P,Waldhauser F.Waveform cross-correlation-based differential traveltime measurements at the Northern California seismic network[J].Bulletin of the Seismological Society of America,2005,95(6):2446-2461

[9] Zhang H J,Thurber T,Rowe C A.Automatic P-wave arrival detection and picking with multiscale wavelet analysis for single-component recordings[J].Bulletin of the Seismological Society of America,2003,93(5):1904-1912

[10] 王振华,袁明生,阎玉魁,等.复杂地表条件下的静校正方法[J].石油地球物理勘探,2003,38(5):487-500 Wang Z H,Yuan M S,Yan Y K,et al.Method of static corrections under complex near-surface conditions[J].Oil Geophysical Prospecting,2003,38(5):487-500

[11] 陈启元,王彦春,段云卿,等.复杂山区的静校正方法探讨[J].石油物探,2001,40 (1):73-81 Chen Q Y,Wang Y C,Duan Y Q,et al.A study on the methods of static correction in complicated mountain area[J].Geophysical Prospecting for Petroleum,2001,40(1):73-81

[12] 吴波,潘树林,陈辉.用四阶累积量子函数改进剩余静校正量的计算[J].石油物探,2010,49(3):227-231 Wu B,Pan S L,Chen H.Improvement of calculating residual statics by fourth-order cumulant subfunction[J].Geophysical Prospecting for Petroleum,2010,59(3):227-231

[13] Aster R C,Rowe C A.Automatic phase pick refinement and similar event association in large seismic data sets[C]∥Thurber C,Rabinowitz N.Advances in seismic event location.Amsterdam:Kluwer Academic Publishing,2000:231-263

[14] Rowe C A,Aster R C,Borchers B,et al.An auto-matic,adaptive algorithm for refining phase picks in large seismic data sets[J].Bulletin of the Seismological Society of America,2002,92(5):1660-1674

[15] 宛新林,席道瑛,高尔根,等.用改进的光滑约束最小二乘正交分解法实现电阻率三维反演[J].地球物理学报,2005,48(1):439-44 Wan X L,Xi D Y,Gao E G,et al．3-D resistivity inversion by the least-squares QR factorization method under improved smoothness constraint condition[J].Chinese Journal Geophysics,2005,48(1):439-444

[16] 吴建平,明跃红,曾融生．遗传算法中的光滑约束反演及其在青藏高原面波研究中的应用[J].地震学报,2001,23(1):45-53 Wu J P,Ming Y H,Zeng R S.Smooth constraint inversion technique in genetic algorithms and its application to surface wave study in the Tibetan plateau[J].Acta Seismologica Sinica,2001,23(1):45-53

[17] Press W H,Flannery B P,Teukolsky S A,et al.Numerical recipes in C[M].2nded.New York:Cambridge University Press,1992:59-70,420-425

(编辑：顾石庆)

The estimation of microseismic residual statics with the constraint of strong-event smoothness

Cheng Leilei,Jiang Yudong,Cui Shuguo,Guo Quanshi

(SinopecGeophysicalResearchInstitute,Nanjing211103,China)

Estimation of residual statics is particularly difficult for microseismic data with low signal-to-noise ratio.Aiming at this problem,a new method for calculating microseismic residual statics is proposed,which combines with the information of mutual cross-correlation of recorded traces in perforation event and the strong-event smoothness constraint condition.This method makes use of the mutual cross-correlation information of the perforation event to increase the amount of information during the estimation of microsesmic residual statics,as well as the strong microseismic events smoothness constraint information after the residual static correction,to improve the precision of residual statics estimation under the low signal-to-noise-ratio condition.Finally,the results of residual statics estimation on numerical and real data prove the robustness and effectiveness of the new method for microseismic data with low signal-to-noise ratio.

microseimic,low signal-to-noise ratio,residual statics,smoothness constraint condition

2015-07-07;改回日期：2015-09-02。

程磊磊(1987—),男,硕士,工程师,现主要从事微地震资料处理方法研究工作。

国家重点基础研究发展计划(973计划)项目“优质页岩气储层预测及精细表征”(2014CB239201)资助。

P631

A

1000-1441(2015)06-0690-09

10.3969/j.issn.1000-1441.2015.06.007