粘弹VTI介质单程波正演模拟与照明分析

陈 雪，韩立国，杨贺龙，段超然

(吉林大学地球探测科学与技术学院，吉林长春130026)

粘弹VTI介质单程波正演模拟与照明分析

陈 雪，韩立国，杨贺龙，段超然

(吉林大学地球探测科学与技术学院，吉林长春130026)

实际地下介质不仅表现各向异性的特征，同时还表现粘弹性的特征，对入射波和反射波的传播及能量分布造成一定的影响。为了更加准确地分析地震波在实际地下介质中的传播规律，利用改进的单程波动方程数值模拟方法，对粘弹VTI介质模型进行qP波正演模拟以及点震源和不同角度入射平面波震源的照明度分析，并对正演及照明结果进行了对比分析。通过两组模型试验，总结了地震波在粘弹VTI介质中与在弹性各向同性介质中传播的不同之处：一方面，介质存在粘弹性会对在其中传播的地震波能量造成吸收；另一方面，介质还存在各向异性，导致地震波在介质中传播速度随方向变化，对地震波的能量分布造成影响。

粘弹性；各向异性；单程波动方程；正演模拟；照明分析

随着地震勘探的目标日趋复杂，油气勘探的难度不断加大，勘探成本不断增加。如何提高地震数据采集、处理和解释过程中的精度并同时降低成本成为油气勘探研究的主要目标。而实际地下介质的复杂性是实现这一目标面临的一个巨大挑战。

理论和实验研究均表明，实际地下介质通常是非完全弹性介质，并且表现出一定的各向异性[1]。因此单纯对弹性各向同性介质的地震波传播特征进行分析已经不能为地震数据的采集和处理提供足够的依据，发展基于粘弹各向异性介质的勘探及分析方法具有很强的理论与现实意义。Carcione等[2-4]研究了粘弹各向异性介质中衰减和品质因子的影响，并计算了相应的波场，为粘弹各向异性介质的正演模拟奠定了基础。吴国忱等[5-7]对粘弹VTI介质中的qP波有限差分正演模拟方法进行了研究，分析了粘弹VTI介质中波场的特点。Zhu等[8]基于弱各向异性的假设使用类Thomsen[9]各向异性参数的形式对衰减系数进行了简化，并描述了TI介质中与衰减相关的平面波振幅畸变。

地震照明分析是一项对地下地震波能量分布进行定量分析的方法技术[10]。照明分析主要分为基于射线正演模拟的射线方法[11-16]和基于波动方程正演模拟的波动方程方法[17]两大类。基于射线理论的照明分析方法计算成本低、速度快，但是由于高频近似以及正演过程中存在射线盲区等方法自身的缺陷，使得射线照明分析方法的精度较低。Campbell等[18]基于射线正演模拟对拖缆采集照明度进行了计算。栗宝鹃[19]也对射线照明分析进行了研究。波动方程法照明分析又分为双程波动方程法与单程波动方程法，双程波动方程法波场信息更丰富，单程波动方程法效率更高。皮红梅[20]采用交错网格有限差分方法进行了双程波动方程的照明分析。Xie等[21]研究了基于单程波动方程的照明分析方法。针对照明分析其它方面的问题，很多学者也进行了研究，巩向博等[22]提出了一种适用于起伏地表条件下的角度域照明分析方法；杨宁[23]对弱各向异性介质的照明度分析进行了研究。

单程波动方程正演模拟适用于复杂介质，比射线方法精度高，比双程波动方程方法计算效率高、成本低。因此本文将单程波动方程方法中的分步傅里叶(slip-step Fourier,SSF)方法[24]拓展到粘弹VTI介质中，对更为接近实际地下介质的粘弹VTI介质模型进行了qP波的正演模拟及点震源和平面波震源的照明度分析，并分析了粘弹VTI介质中qP波的传播及能量分布特点，为粘弹各向异性介质的数据采集和处理提供一些参考。

1 方法原理

1.1 粘弹VTI介质单程波正演模拟原理

SSF方法通过定义参考慢度和扰动慢度来处理地震波传播过程中介质的横向速度变化[24]，将地震波的传播过程分解为基于参考慢度的一次相移过程和基于扰动慢度的二次相移过程。二维情况下，SSF方法地震波正向延拓公式为:

(1)

其中，

(2)

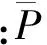
根据粘弹VTI介质的应力应变关系可以推导出粘弹VTI介质的波动方程，将二维平面波解U=uei(ω t-kxx-kzz)代入波动方程则得到粘弹VTI介质的Kelvin-Christoffel方程，即：

(3)

其中，

(4)

式中：cij(i,j=1,2,…，6)为弹性系数；ηij(i,j=1,2,…，6)为粘弹性衰减系数；ux，uy，uz分别为平面波振幅在x，y，z方向上的分量，在二维情况下uy为0。

为了获得方程(3)的非零解，要求Christoffel行列式必须为0，即：

det(G)=0

(5)

式中：G为方程(3)中的系数矩阵。求解(5)式则可得到粘弹VTI介质qP波和qS波耦合的频散关系方程。为了消除波场中横波的干扰，根据Alkhalifah[25-26]提出的声学近似假设，令横波速度vS为0，可以得到粘弹VTI介质qP波频散关系方程。用Thomsen各向异性参数(ε,δ)表示弹性参数，并用品质因子Q表示粘弹性衰减系数，整理得到粘弹VTI介质qP波频散关系式为：

(6)

(7)

对(7)式进行Taylor展开，则扰动介质的垂直波数为:

(8)

将(7)式和(8)式代入方程(1)，得到粘弹VTI介质中的波场正向延拓方程。使用插值方法处理各向异性的横向变化，在每一个深度间隔内选择最小和最大的各向异性参数ξ1，η1和ξ2，η2，并使用这两组参数同时延拓波场，即:

(9)

插值得到最终的波场为：

(10)

1.2 照明度分析原理

将粘弹VTI介质的正演模拟引入到照明度分析中，分析粘弹VTI介质中地震波的传播特征及能量分布。照明度分析可以分为以下几大类型。

1.2.1 单向照明

在某一观测系统下，激发点震源，并将波场传播到地下各个点，得到的照明强度称为点源照明，根据能量理论，地下空间某点(x,y)处的点源照明强度定义为：

(11)

式中：Ns为震源个数；[ω1,ω2]为地震频带范围。

根据互易定理，检波点照明相当于在检波点处设置震源，因此检波点照明度计算与点源照明计算方法相一致，即：

(12)

式中：Ng为检波器个数。采集系统源或检波器的照明方式称为单向照明。

1.2.2 双向照明

单向照明只考虑了震源或检波器与地下介质结构对地震波传播的影响，不能反映整个观测系统的影响，因此，为了综合分析整个观测系统和地质构造对地震波传播的影响，人们发展了双向照明的概念，在震源处放置震源，根据源检互易定理在检波器处也放置震源，同时记录入射场和散射场，分析地下能量分布。则地下空间某点(x,y)处的双向照明计算公式为：

(13)

1.2.3 平面波照明

除点震源照明外，还可以进行平面波照明，通过同时或按一定的时间间隔延时激发点震源，根据惠更斯原理可以近似模拟不同角度入射的平面波，对于频率域的单程波正演模拟，根据傅里叶变换的性质，有：

(14)

式中：s为震源函数。延时的时间间隔Δt与平面波入射角θ的关系为：

(15)

式中：ds为炮间距；v1为地表速度。平面波照明定义式与点源照明定义式形式相同。

2 模型试验

2.1 粘弹VTI介质单程波算法正演模拟

为了验证单程波算子的正确性，首先建立一个逆断层模型(图1)，3层速度分别为2500，3000，3500m/s。第1层和第3层为弹性各向同性层，第2层为各向异性层且各向异性参数ε=-0.1，δ=-0.2，震源位于第175道，震源主频为40Hz。图2为使用不同方法计算的无衰减情况下逆断层模型250ms的波场快照以及对应的波场快照局部放大显示。由于SSF方法本身不能处理各向异性的横向变化，只能使用背景各向异性值进行计算，结果不准确。从图2可以看出，改进后的SSF方法能够处理各向异性的横向变化，与双程波方法波场更为接近。

图1 逆断层模型示意

图2 双程波动方程算法(a)、改进单程波动方程算法(b)和原始单程波动方程算法(c)计算的无衰减情况下逆断层模型250ms波场快照

对逆断层模型第2层取不同各向异性参数和衰减条件时，计算对应的qP波地震记录如图3所示。各向异性条件下qP波走时与各向同性条件下明显不同，且其变化程度受各向异性参数影响。当ε和δ均为正时，各向异性介质中非垂直入射的qP波传播速度较各向同性介质中快，导致各向异性情况下非零偏移距的走时更短。反之，当ε和δ均为负时，各向异性介质中非垂直入射的qP波速度较各向同性介质中慢，各向异性情况下非零偏移距的走时更长。当第2层介质有衰减时，无论各向同性还是各向异性介质，下层界面的反射波能量均被吸收，反射波振幅减弱。其模拟结果与理论分析结果相符，证明了该方法的正确性。

图4为图3中所示的地震记录中第250道的时频分析结果。从图4中可以看出，上层界面的反射波由于不受下方介质的影响在6幅图中保持相同的时间位置和形态，而下层界面的反射波由于受第2层介质的影响其时间分布在各向异性情况和各向同性情况下有所差别，ε，δ同时为正时，其时频能量上移，ε，δ同时为负时，其时频能量下移。第2层介质的粘滞性导致第2个界面反射波的时频能量衰减严重(图4d，图4e，图4f)。

2.2 粘弹VTI介质单程波算法照明分析

本文主要分析地下介质的粘弹性和各向异性性质对地震波能量分布的影响，因此只对源照明和平面波照明进行计算分析。

对2.1节中的逆断层模型进行源照明度计算，结果如图5所示。从图5中可以看出，由于地下介质速度变化，地震波能量分布不均匀，逆断层对其下方介质造成一定程度的能量屏蔽。此外，受介质各向异性和衰减的影响，粘弹各向异性介质的能量分布与弹性各向同性介质也有所不同。当ε和δ均为正值时(图5b，图5e)，相对于各向同性情况(图5a，图5d)第2层介质中的地震波能量分布形态明显呈收缩汇聚状态，第3层介质中的能量分布形态也呈现一定程度的收缩。当ε和δ均为负时(图5c，图5f)，相比各向同性情况第2层介质中的地震波能量分布明显呈扩张发散状态，第3层也呈现相同现象。且由于第2层介质存在粘滞性，各向同性和各向异性情况下都会对地震波能量造成吸收，导致模型第2层及第3层的地震照明强度明显弱于弹性情况。

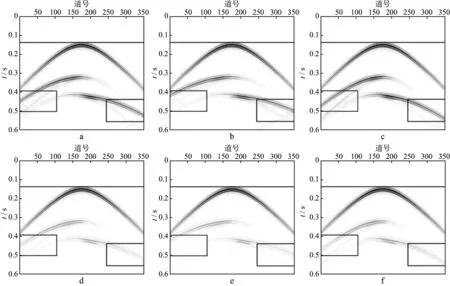
图3 第2层介质不同参数条件下的逆断层模型qP波正演记录

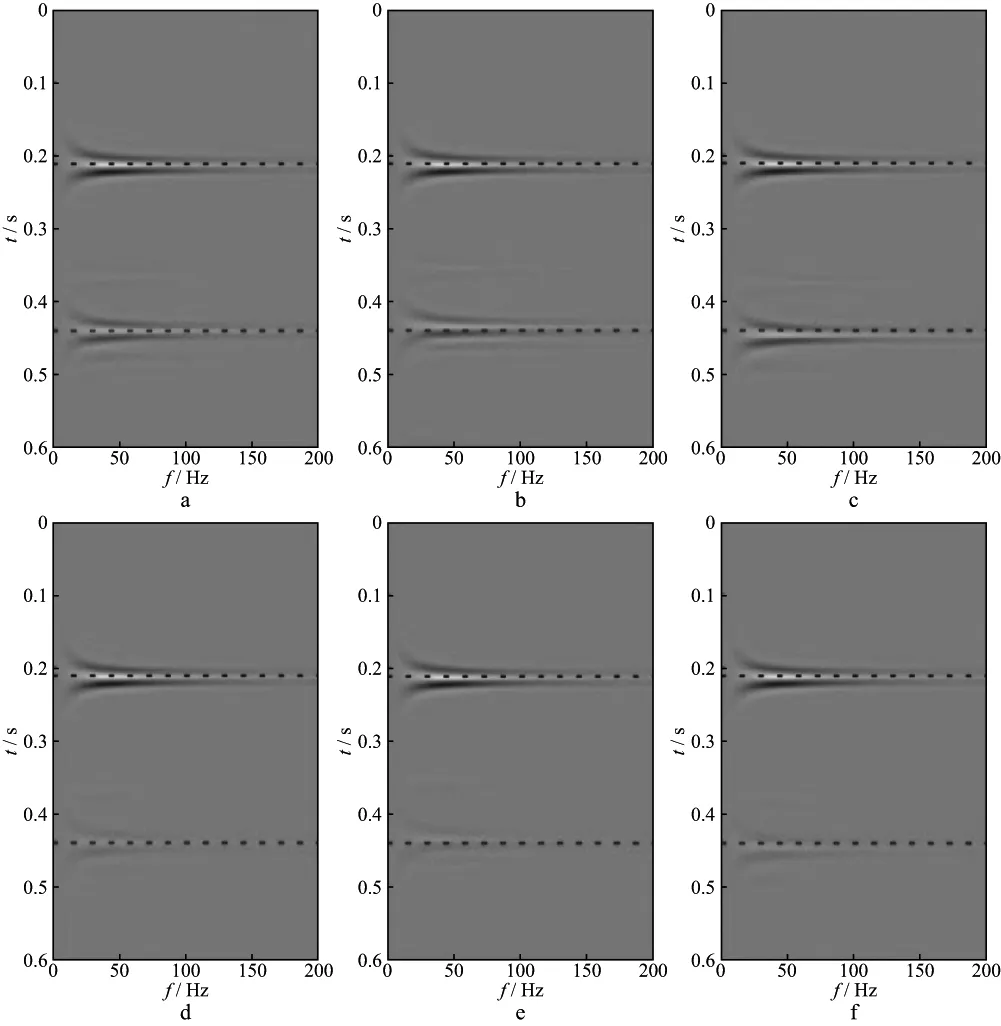
图4 图3中地震记录第250道时频分析结果

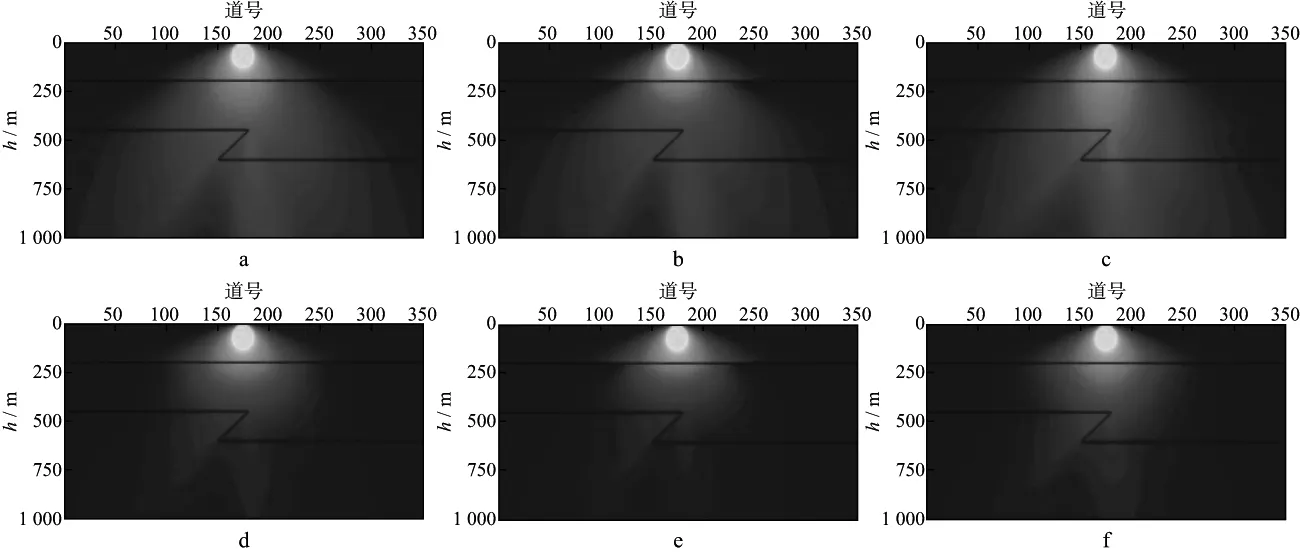
图5 第2层介质不同参数条件下的qP波照明结果

抽取逆断层模型250m和750m深度处介质的照明能量分布，如图6所示。从图6中可以更直观地看出，各向同性与各向异性照明能量在同一位置的强度差别，在各向异性参数均为正值时照明能量总体呈现偏低趋势，在各向异性参数均为负值时照明能量总体呈现偏高趋势，而介质的粘滞性减弱了整体的地震波照明强度。

图7为一个盐丘模型示意图，盐丘为高速侵入体，顶部会对下方造成能量屏蔽，导致两翼处照明强度不足，分别对盐丘模型在弹性各向同性、粘弹各向同性、弹性各向异性和粘弹各向异性4种不同介质参数情况下进行照明分析。在模型包含粘滞性时，将第1层、第5层和盐丘本身的Q值取为10000，表示介质对地震波能量没有吸收，盐丘模型具体参数见表1。

图6 逆断层模型不同介质参数情况下250m(a)和750m(b)深度处照明能量分布

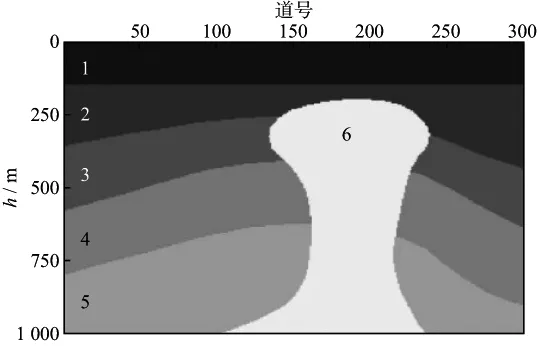
图7 盐丘模型示意

表1 盐丘模型参数

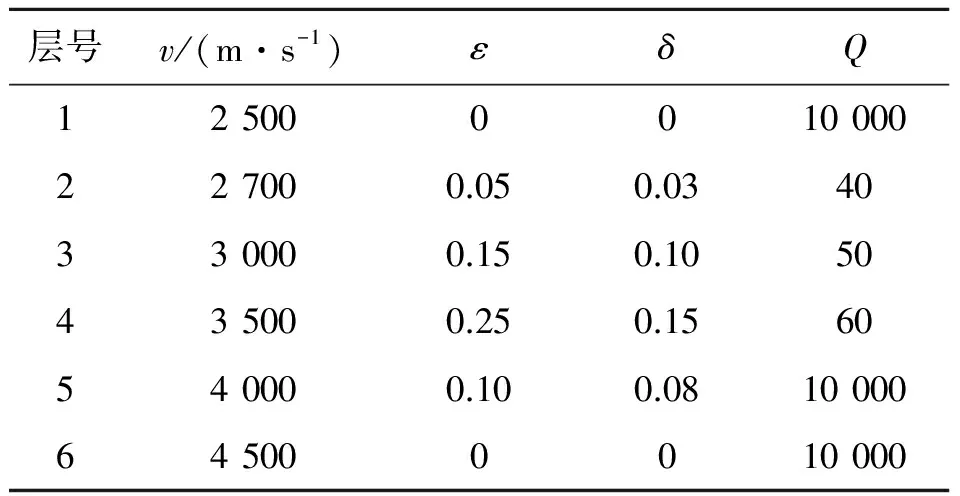
层号v/(m·s-1)εδQ125000010000227000．050．0340330000．150．1050435000．250．1560540000．100．0810000645000010000

图8和图9分别为盐丘模型不同介质参数情况下平面波0和20°入射时的照明能量分布结果。

图8 盐丘模型弹性各向同性(a)、粘弹性各向同性(b)、弹性各向异性(c)和粘弹性各向异性(d)情况下平面波0入射照明能量分布

图9 盐丘模型弹性各向同性(a)、粘弹性各向同性(b)、弹性各向异性(c)和粘弹性各向异性(d)情况下平面波20°入射照明能量分布

平面波垂直入射时，介质横向速度变化导致平面波波前面弯曲，波的传播受到介质各向异性的影响，照明分布与各向同性介质有一定差别，在图中椭圆区域表现明显。当平面波以20°入射角入射到地下介质中时，波前面传播到各向异性层就会受到介质各向异性的影响，引起地震波能量分布的变化，在椭圆区域表现较为明显。受介质粘滞性的影响，衰减层及其下方地层的照明能量整体减弱(图8b，图8d，图9b，图9d)。

抽取盐丘模型不同介质参数情况下平面波入射600m深度处的照明能量分布，结果如图10所示。图10更直观地反映了各向异性及衰减参数对地震波能量分布的影响，各向异性导致地震波能量分布极值位置变化；由于模型总体处于弱各向异性情况，且各向异性参数为正值，照明能量总体表现为略低于各向同性情况，而介质粘弹性的存在导致整体的照明强度均降低。

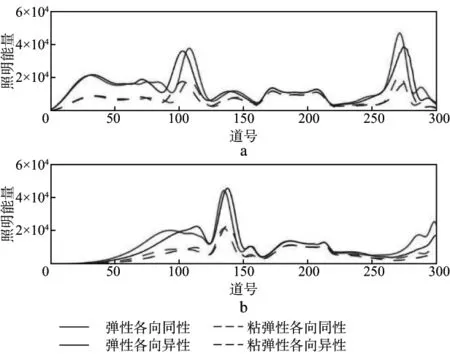
图10 盐丘模型不同介质参数情况下平面波0入射(a)和20°入射(b)在600m深度处的照明能量分布

3 结束语

实际地下介质中普遍存在粘弹各向异性的性质。研究粘弹各向异性介质中地震波的传播规律对指导地震数据采集、处理和解释十分重要。单程波数值模拟方法能够适应复杂介质，波场清晰，易于实现且计算效率高，成本低。但原始的SSF算法只能利用介质的背景各向异性参数进行计算，不能处理介质的横向各向异性变化。本文将SSF算法拓展到粘弹VTI介质中，使其能够同时适应介质粘弹性和各向异性的变化。模型计算验证了本文方法的正确性。

使用改进的SSF方法对数值模型进行了正演模拟与照明分析，试验发现粘弹各向异性情况下地震波的传播规律与弹性各向同性情况下有很大区别。一方面，由于地下介质具有粘弹性，对在其中传播的地震波能量造成吸收，导致反射波的振幅减小，地震波照明能量减弱。另一方面，由于地下介质具有各向异性，地震波走时和照明分布与各向同性情况相比也有很大不同。

[1] Lucet N,Zinszner B.Effects of heterogeneities and anisotropy on sonic and ultrasonic attenuation in rocks[J].Geophysics,1992,57(8):1018-1026

[2] Carcione J M.Wave propagation in anisotropic linear viscoelastic media:theory and simulated wavefields[J].Geophysical Journal International,1990,101(3):739-750

[3] Carcione J M,Cavallini F.Attenuation and quality factor surfaces in anisotropic-viscoelastic media[J].Mechanics of Materials,1995,19(4):311-327

[4] Carcione J M.Wave fields in real media:wave propagation in anisotropic,anelastic,porous and electromagnetic media[M].2nded.Amsterdam:Elsevier Science,2007:1-538

[5] 吴国忱,梁锴.VTI介质频率-空间域准P波正演模拟[J].石油地球物理勘探,2005,40(5):535-545 Wu G C,Liang K.Quasi P wave forward modeling in frequency space domain in VTI media[J].Oil Geophysical Prospecting,2005,40(5):535-545

[6] 吴国忱.各向异性介质地震波传播与成像[M].东营:中国石油大学出版社,2006:1-293 Wu G C.Seismic wave propagation and imaging in anisotropy media[M].Dongying:China University of Petroleum Press,2006:1-293

[7] 吴国忱,梁锴.VTI介质qP波方程高精度有限差分算子[J].地球物理学进展,2007,22(3):896-904 Wu G C,Liang K.High precision finite difference operators for qP wave equation in VTI media[J].Progress in Geophysics,2007,22(3):896-904

[8] Zhu Y,Tsvankin I.Plane-wave propagation in attenuative transversely isotropic media[J].Geophysics,2006,71(2):T17-T30

[9] Thomsen L.Weak elastic anisotropy[J].Geophysics,1986,51(10):1954-1966

[10] 陈生昌,马在田,吴如山.波动方程双程地下方向照明分析[J].同济大学学报(自然科学版),2007,35(5):681-684,704 Chen S C,Ma Z T,Wu R S.Two-way subsurface directional illumination analysis by wave equation[J].Journal of Tongji University (Natural Science),2007,35(5):681-684,704

[11] Bear G,Lu R,Lu C P,et al.The construction of subsurface illumination and amplitude maps via ray tracing[J].Expanded Abstracts of 69thAnnual Internat SEG Mtg,1999,1532-1535

[12] Bear G,Lu C P,Lu R,et al.The construction of subsurface illumination and amplitude maps via ray tracing[J].The Leading Edge,2000,19(7):726-728

[13] Muerdter D R,Ratcliff D W.Subsalt illumination determined by ray-trace modeling:a catalog of seismic amplitude distortions caused by various salt shapes[J].Expanded Abstracts of 70thAnnual Internat SEG Mtg,2000,733-736

[14] Muerdter D,Ratcliff D.Understanding subsalt illumination through ray trace modeling,part 1:simple 2-D salt models[J].The Leading Edge,2001,20(6):578-594

[15] Muerdter D,Kelly M,Ratcliff D.Understanding subsalt illumination through ray-trace modeling,part 2:dipping salt bodies,salt peaks,and nonreciprocity of subsalt amplitude response[J].The Leading Edge,2001,20(7):688-697

[16] Muerdter D,Ratcliff D.Understanding subsalt illumination through ray-trace modeling,part 3:salt ridges and furrows,and the impact of acquisition orientation[J].The Leading Edge,2001,20(8):803-816

[17] Fontecha B,Cai W Y,Ortigosa F,et al.Wave equation migration and illumination on a 3-D GOM deep water dataset[J].Expanded Abstracts of 75thAnnual Internat SEG Mtg,2005,1989-1993

[18] Campbell S,Pramik B,Cafarelli B.Comparative ray-based illumination analysis[J].Expanded Abstracts of 72ndAnnual Internat SEG Mtg,2002,41-44

[19] 栗宝鹃.基于射线理论的照明分析[D].青岛:中国石油大学(华东),2007 Li B J.Illumination analysis based on ray tracing theory[D].Shandong:China University of Petroleum (East China),2007

[20] 皮红梅.双程波动方程数值模拟和照明分析方法研究[D].长春:吉林大学,2009 Pi H M.Method research on two-way wave-equation forward modeling and illumination analysis[D].Changchun:Jilin University,2009

[21] Xie X B,Jin S W,Wu R S.Wave-equation-based seismic illumination analysis[J].Geophysics,2006,71(5):S169-S177

[22] 巩向博,吕庆田,韩立国,等.起伏地表地震波场角度域照明分析[J].吉林大学学报(地球科学版),2013,43(2):610-615 Gong X B,Lv Q T,Han L G,et al.Method of angle-domain illumination analysis on rugged surface[J].Journal of Jilin University (Earth Science Edition),2013,43(2):610-615

[23] 杨宁.弱各向异性单程波波动方程数值模拟新方法研究[D].成都:成都理工大学,2011 Yang N.Method research of weak-anisotropy’s one-way wave-equation seismic numerical simulation[D].Chengdu:Chengdu University of Technology,2011

[24] Stoffa P L,Fokkema J T,de Luna Freire R M,et al.Split-step Fourier migration[J].Geophysics,1990,55(4):410-421

[25] Alkhalifah T.Acoustic approximations for processing in transversely isotropic media[J].Geophysics,1998,63(2):623-631

[26] Alkhalifah T.An acoustic wave equation for anisotropic media[J].Geophysics,2000,65(4):1239-1250

(编辑：顾石庆)

One-way wave equation forward modeling and illumination analysis in viscoelastic VTI media

Chen Xue,Han Liguo,Yang Helong,Duan Chaoran

(CollegeofGeo-explorationScienceandTechnology,JilinUniversity,Changchun130026,China)

The actual subsurface media always show anisotropic and viscoelastic properties which will affect the propagation and the energy distribution of the seismic wave.In order to analyze the laws of qP wave propagation in viscoelastic anisotropic media more accurately,an improved one-way wave forward modeling method is used to calculate the qP wavefield and qP wave illumination intensity of the point source and plane wave source with different incident angles in viscoelastic VTI media.Differences between the wave propagation in viscoelastic VTI media and elastic isotropic media are clarified by two sets of experiment:for one thing the media will absorb the energy of the seismic wave due to the existence of the viscoelasticity; for another the seismic wave velocity will vary with the propagation direction due to the anisotropy of the media which will affect the energy distribution of the wave.

viscoelasticity,anisotropy,one-way wave equation,forward modeling,illumination analysis

2015-02-04;改回日期：2015-05-24。

陈雪(1989—)，女，博士在读，主要从事各向异性正、反演与储层研究工作。

韩立国(1961—)，男，教授，博士生导师，主要从事地震数据处理与解释方面的研究工作。

国家高技术研究发展计划(863计划)项目(2014AA06A605)和国家自然科学基金项目(41374115)联合资助。

P631

A

1000-1441(2015)06-0643-09

10.3969/j.issn.1000-1441.2015.06.002