磁流体的Shliomis体积特性研究

卜胜利, 吴龙龙

(上海理工大学理学院,上海 200093)

磁流体的Shliomis体积特性研究

卜胜利, 吴龙龙

(上海理工大学理学院,上海 200093)

根据Shliomis体积满足的解析关系式,理论分析了磁性颗粒浓度、环境温度和外磁场强度与方位对磁流体的Shliomis体积的影响,并通过数值模拟计算进行了定量的研究.结果表明,磁流体的Shliomis体积随磁性颗粒浓度的增加而增加;随环境温度的增加而减小,在远离磁流体熔点温度时趋于稳定值;随外磁场强度的增加而增加,且与外磁场和磁矩方位夹角有关.纵观各种因素,磁流体的黏度对其Shliomis体积的影响起着关键的作用.研究结果有助于深入了解磁流体中固体磁性颗粒磁矩的弛豫现象.

磁流体;Shliomis体积;浓度;温度;磁场

磁流体是由纳米级的固体磁性颗粒分散在载液中所形成的稳定胶体体系,它既具有液态物质的流动性,又具有磁性物质的强磁性,通常呈现超顺磁性,是一种新型的功能材料[1-3].磁流体内的磁性颗粒尺寸通常在10 nm左右,一般小于单畴颗粒临界尺寸,因此,可以认为磁流体中的固体颗粒是单畴粒子.对于由多个磁性颗粒组成的宏观介质,各个磁畴磁矩的排列杂乱无章,磁矩方向矢量和为零,总的磁矩为零,因此,磁流体一般对外不显磁性.磁流体在外磁场的作用下会形成丰富的微观结构,这些微观结构使得磁流体具有许多独特的磁光特性,如磁致折射率变化、法拉第旋光效应、磁二向色性、磁光克尔效应等.据此可以将磁流体应用于磁光开关、磁光隔离器、磁光调制器、粗波分复用器、磁场传感器等光学器件中[4-8].光学各向异性是磁流体的重要磁光特性之一,其性质的强弱主要取决于固体磁性颗粒的空间位置和分布以及磁流体场诱导的链状结构的取向.

磁流体的Shliomis体积是决定磁流体中固体磁性颗粒的磁矩在外磁场变化后通过何种机制弛豫到热平衡态的临界体积[9].当固体磁性颗粒的体积大于Shliomis体积时,磁性颗粒主要通过Brown弛豫到热平衡态,伴随弛豫过程的发生,可能会产生磁流体的各向异性,磁流体对外显示出超顺磁性.而当固体磁性颗粒体积小于Shliomis体积时,磁性颗粒主要通过Néel弛豫到热平衡态,其对磁流体的各向异性没有贡献,磁流体体现内禀超顺磁性[10-11].因此,磁流体的Shliomis体积作为区分Brown弛豫和Néel弛豫的一个重要临界体积,研究其与各种物理参数的关系及规律具有重要的意义,进而为磁光领域的磁流体设计、制备提供有益的指导.本文借助理论分析,数值计算了磁流体的Shliomis体积与各种参数的依赖关系,有关结果有助于深入理解磁流体的磁矩弛豫及磁性颗粒团聚的物理机制,对磁流体的磁光应用有一定的参考价值,从而指导基于磁流体的磁光器件的设计与制作.

1 理论基础

磁流体中固体磁性颗粒的磁矩在外磁场变化后弛豫到热平衡态通常有两种不同机理,即Brown弛豫和Néel弛豫.在外磁场改变后,磁性颗粒自身磁矩和外磁场相互作用,若磁性颗粒内部的磁矩随磁性颗粒本身一起旋转而达到热平衡态,颗粒的空间位置发生改变,这种弛豫过程称作Brown弛豫,其特征弛豫时间[1,9,12-13]τB=3ηV′g/(kBT) (1)式中,η为磁流体的黏度;V′为颗粒的流体动力学体积;g为几何因子(g=1时为球形颗粒);T为绝对温度;kB为波尔兹曼常数.

若磁性颗粒本身不动,由磁性颗粒内部的磁矩矢量独立于颗粒几何形状旋转而达到热平衡态,颗粒的空间位置不发生改变,只是磁矩的方向发生改变,这种弛豫过程称作Néel弛豫,其特征弛豫时间[1,10-11,14-15]

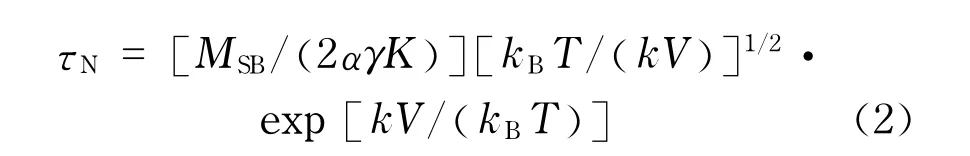
式中,MSB为磁性颗粒的饱和磁化强度;α为衰减因子;γ为旋磁比;K为有效各向异性常数;V为磁性颗粒的体积,通常可取V≈V′.

在实际的磁流体中,固体颗粒经历何种弛豫过程与Néel弛豫和Brown弛豫特征时间的大小直接相关,起主导作用的弛豫过程是拥有较短弛豫时间的弛豫过程,即固体颗粒内磁矩的实际弛豫时间τ满足如下关系[1]:

对于给定的磁流体,其固体颗粒尺寸决定着磁流体主要通过哪种弛豫达到平衡.由式(1)可以看出τB与固体颗粒体积成正比,而式(2)表明τN随固体颗粒体积的变化而发生显著的变化(远大于一次方的线性正比关系),因此,只有小体积的磁性颗粒的磁矩弛豫由Néel弛豫主导.而对于大体积的磁性颗粒,其磁矩弛豫由Brown弛豫主导,此时固体颗粒本身的非均匀性会对磁流体的各向异性有影响.

由式(1)-(3)可计算出τB,τN和τ随磁性颗粒体积的变化关系,如图1所示,图1中取η= 100 mm2/s.

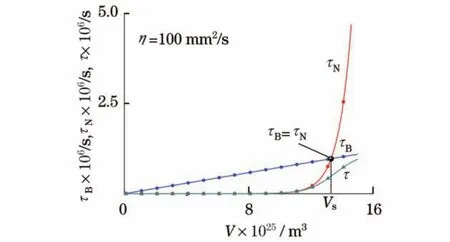
图1 磁性颗粒的弛豫时间与体积的关系Fig.1 Relaxation time as a function of volume of magnetic nanoparticle

由式(3)及图1可知,当τN≪τB时,Néel弛豫占主导作用;当τB≪τN时,Brown弛豫占主导作用.在Néel弛豫占主导和Brown弛豫占主导之间有个临界弛豫时间,即满足关系τN=τB,此时磁性颗粒体积V=Vs,Vs为磁流体的Shliomis体积.根据式(1)和式(2),磁流体的Shliomis体积Vs可由下式求出(取g=1):

其中

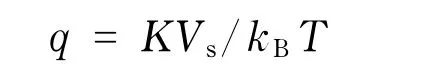
现以式(4)为基础对磁流体的Shliomis体积特性进行分析研究.

2 影响磁流体的Shliomis体积的因素分析

式(4)表明,黏度、温度对磁流体的Shliomis体积Vs有直接的影响.而磁流体的黏度与诸多参数有关,因此,其它参数通过影响磁流体的黏度间接地影响其Shliomis体积Vs.固体磁性颗粒的种类、形状、浓度,基液的类型,表面活性剂的种类和浓度等都可以影响磁流体的黏度.在外磁场作用下,磁性颗粒的磁矩会与外磁场相互作用,因此,外磁场也影响磁流体的黏度.这些参数是影响磁流体的Shliomis体积的重要因素.本文通过讨论固体颗粒浓度、环境温度和外磁场强度与方向这3个主要因素对磁流体黏度的影响来研究磁流体Shliomis体积与诸参数的关系.

2.1 磁性颗粒浓度的影响

一般情况下,无外磁场作用时,磁流体的黏度远大于其基载液的黏度,其最早的黏度理论模型是由Einstein于1906年创立,其黏度η可表示为[1]

但是,这个黏度公式仍然有局限,一般磁流体中,黏度随着浓度变化是有限的,但式(6)体现不出.之后, Rosensweig对式(6)进行了进一步的修正,修正后的磁流体黏度表达式为[16]

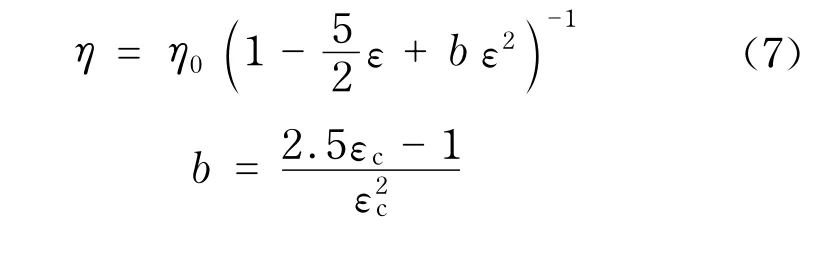
式中,η0为磁流体载液的黏度;ε为悬浮磁性颗粒的体积分数.

Einstein公式给出的黏度与浓度呈线性关系,它仅适用于高倍稀释的磁流体,而对高浓度的磁流体,则误差较大.Batchelor对Einstein公式进行了改进,其给出的黏度表达式适用于高浓度的磁流体,具体为[12]

式中,εc为等直径球形固体颗粒最大密度堆砌时对应的体积分数,即εc=0.74.

由式(5)和式(7)可画出磁流体的黏度η与磁性颗粒浓度的变化关系,如图2所示.图2中取固体颗粒平均直径d=10 nm,表面活性剂层厚度s= 2 nm.由图2可以看出,Rosensweig公式给出的黏度与Einstein公式给出的黏度相比,两者在低浓度时(约在0～10%)比较接近,但在较高浓度时差距非常大.因此,在讨论磁性颗粒浓度对磁流体黏度的影响(进而对其Shliomis体积影响)时,尽可能采用Rosensweig给出的黏度公式,特别是对高浓度磁流体.

图2 磁流体的黏度与磁性颗粒浓度的关系Fig.2 Viscosity of magnetic fluid vs the volume fraction of magnetic nanoparticle

2.2 环境温度的影响

磁流体的黏度随温度的变化关系的经验公式描述为[10-11]

式中,A为正的特征常数;T0是该磁流体的熔点温度.

对煤油基Fe3O4磁流体,Shliomis和Stepanove给出η0=5.77×10-3m2/s,A=396 K和T0= 162 K的经验常数.由式(8)可画出磁流体的黏度随温度的变化关系,如图3所示(见下页).图3表明,磁流体的黏度随温度的增加而减小,特别是在接近磁流体熔点温度附近,黏度变化非常迅速,而当温度远高于熔点温度时,磁流体的黏度随温度的变化比较缓慢.通常情况下,磁流体的温度是远高于熔点温度的,因此,温度对磁流体Shliomis体积的影响主要体现在对式(4)中q值的影响.

2.3 外磁场强度与方向的影响

在外磁场作用下,磁流体中的固体颗粒会沿着磁场方向排列.假设在排列的过程中,颗粒固有磁矩方向与颗粒形状保持一致(Brown弛豫),同时忽略固体颗粒之间的相互作用.对于固体颗粒磁矩与磁场相互作用有两种极端情况,即固体颗粒的磁矩垂直于磁场和固体颗粒的磁矩平行于磁场.当磁场和固体颗粒磁矩方向垂直时,固体颗粒受到一个额外的磁力矩使得其旋转,从而影响磁流体的黏度.当磁场和固体颗粒磁矩方向平行时,固体颗粒不受磁力矩作用,因而磁场对黏度没有影响.因此,磁场的大小和方向对磁流体的黏度均有影响.通常,磁流体的黏度随磁场的变化关系可描述为[15,17-18]

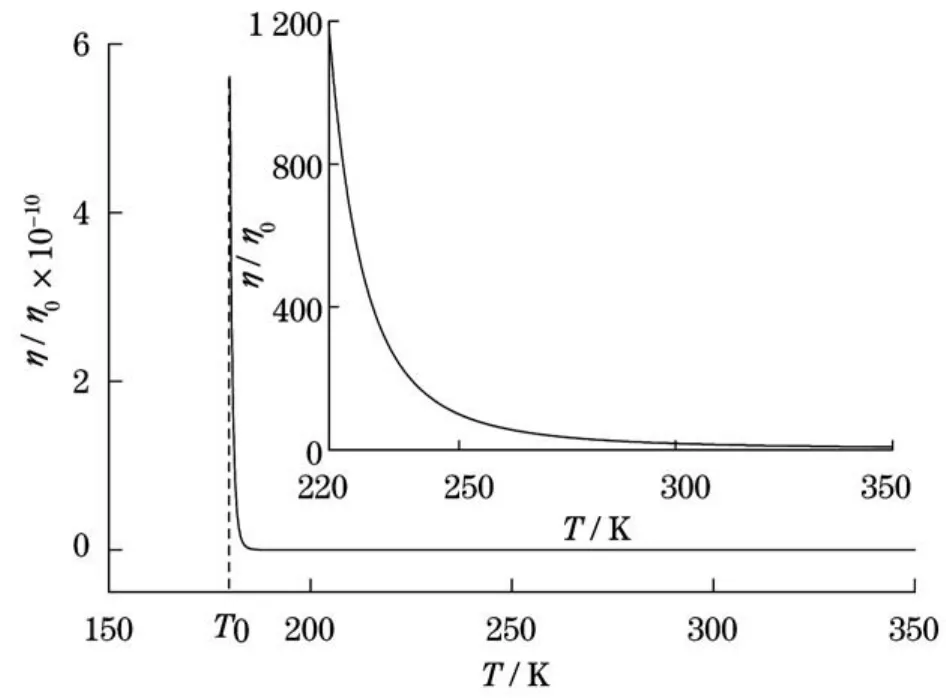
图3 磁流体的黏度随温度的变化关系Fig.3 Viscosity of magnetic fluid as a function of temperature

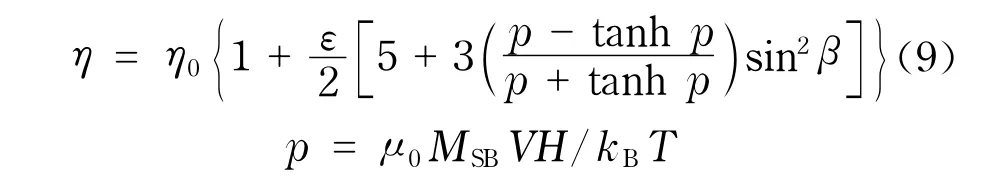
式中,β为磁场与固体颗粒磁矩方向的夹角;μ0为真空磁导率;H为外磁场强度.

由式(9)可以导出磁流体在一些特殊和极端参数情况下的黏度为

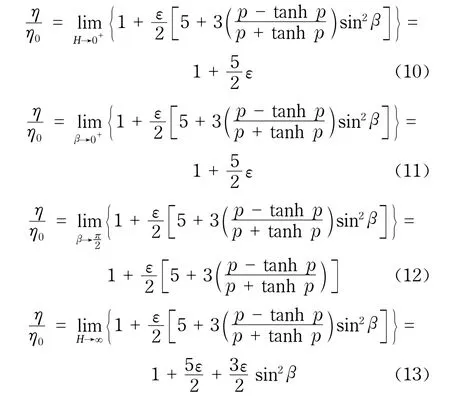
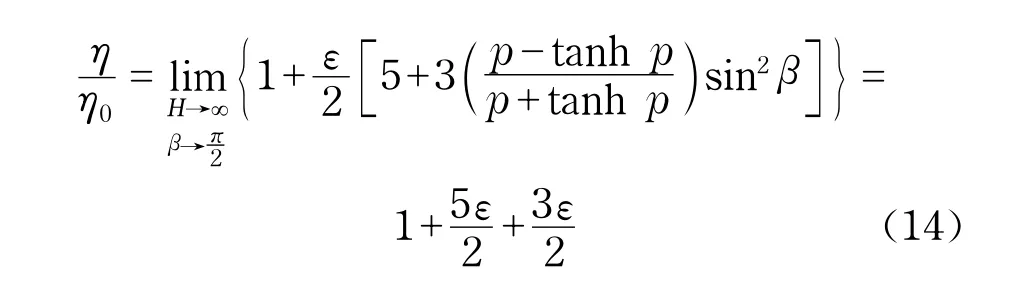
由式(10)和式(11)可以看出,Einstein公式(5)是式(9)在特殊情况下的结果,当磁场强度趋于零或外磁场方向与颗粒磁矩方向的夹角趋于零时,式(9)即简化为Einstein公式.比较式(14)和式(5)可以发现,外磁场的作用使得磁流体的黏度增加,其影响的极限值为(3ε/2)η0.

由式(9)可画出磁流体的黏度随外磁场强度及方位角β的关系,如图4所示,图4中取ε=0.1.

图4 磁流体的黏度与外磁场强度和方向的变化关系Fig.4 Viscosity of magnetic fluid as a function of strength and azimuthal angle of magnetic field

图4及式(12)和式(13)均表明,磁场越大或者外磁场方向与颗粒磁矩方向的夹角越大,磁流体的黏度就越大.图4还表明,磁场对磁流体黏度的影响呈现非牛顿流体力学特性.

3 数值结果与讨论

前述的理论分析表明,磁流体的浓度、环境温度、外磁场强度与方向等参数的改变都将直接或间接地影响磁流体的Shliomis体积.现通过数值模拟计算具体地讨论各主要参数对磁流体的Shliomis体积的影响及其规律.

3.1 浓度和温度对磁流体Shliomis体积的影响

当环境温度固定时,由式(4)和式(7)可计算出磁流体的Shliomis体积与磁性颗粒浓度的变化关系,如图5所示.图5表明,在固定温度下,磁流体的Shliomis体积随磁性颗粒浓度的增加而单独地增加.而当磁性颗粒浓度固定时,磁流体的Shliomis体积随环境温度的增加而单调地减小.

图5 不同温度下磁流体的Shliomis体积与磁性颗粒浓度的变化关系Fig.5 Shliomis volume of magnetic fluid as a function of magnetic nanoparticle concentration at various temperatures

对于低浓度Fe3O4磁流体,实验数据表明,其熔点温度T0与浓度的关系为

由式(4)、式(8)和式(15)可计算出低浓度磁流体的Shliomis体积随环境温度和磁性颗粒浓度的变化关系,如图6所示.

图6 磁流体的Shliomis体积随环境温度和磁性颗粒浓度的变化关系Fig.6 Shliomis volume of magnetic fluid vs magnetic nanoparticle concentration and ambient temperature

由图6可以得出,当磁性颗粒浓度固定时,磁流体的Shliomis体积与环境温度的变化关系,如图7所示.

图6和图7表明,当温度变化时,磁流体的Shliomis体积在其熔点温度附近随温度的增加迅速减小,而在远离熔点温度时逐渐减小到最小值,之后随温度的增加而缓慢增加.

3.2 外磁场对磁流体Shliomis体积的影响

同理,由式(4)和式(9)可计算出磁流体的Shliomis体积随外磁场强度与方位的关系,如图8所示.

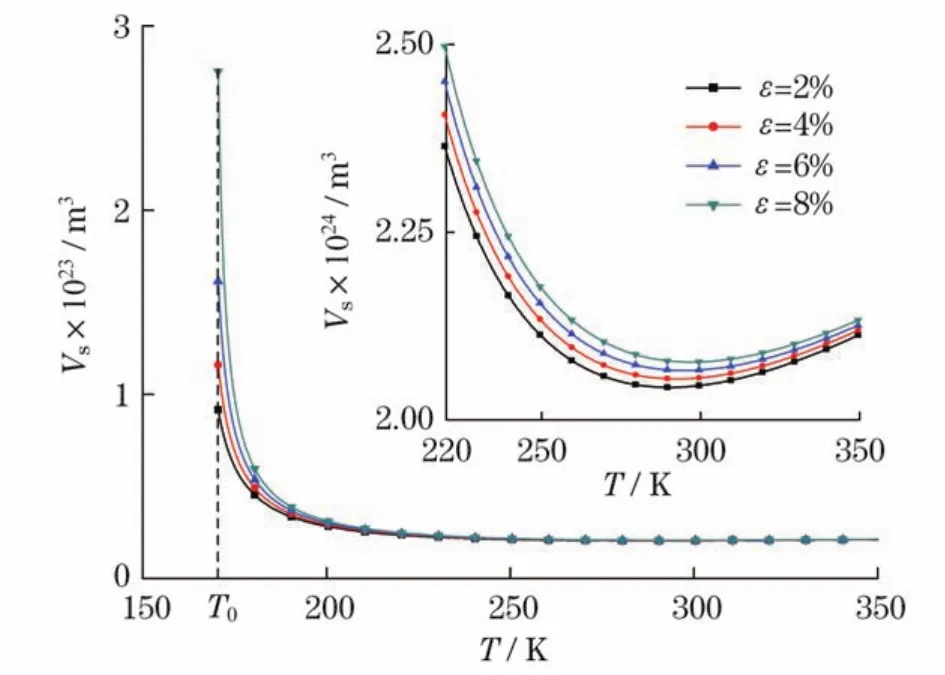
图7 不同磁性颗粒浓度时磁流体的Shliomis体积随环境温度的变化关系Fig.7 Shliomis volume of magnetic fluid as a function of temperature at various magnetic nanoparticle concentrations

图8 磁流体的Shliomis体积随外磁场强度和方位角的变化关系Fig.8 Shliomis volume of magnetic fluid vs the strength and azimuthal angel of externally applied magnetic field

由图8可进一步得出,当外磁场方位角固定时,磁流体的Shliomis体积与外磁场强度的变化关系,如图9所示(见下页).

图8和图9表明,外磁场强度越大,磁流体的Shliomis体积就越大;外磁场与固体颗粒磁矩夹角越大,磁流体的Shliomis体积也越大.

从上述结果可以看出,磁流体的Shliomis体积随磁性颗粒浓度、环境温度和外磁场的变化规律与磁流体黏度随各参数的变化规律类似.因此,黏度对磁流体的Shliomis体积具有直接的、重要的影响.

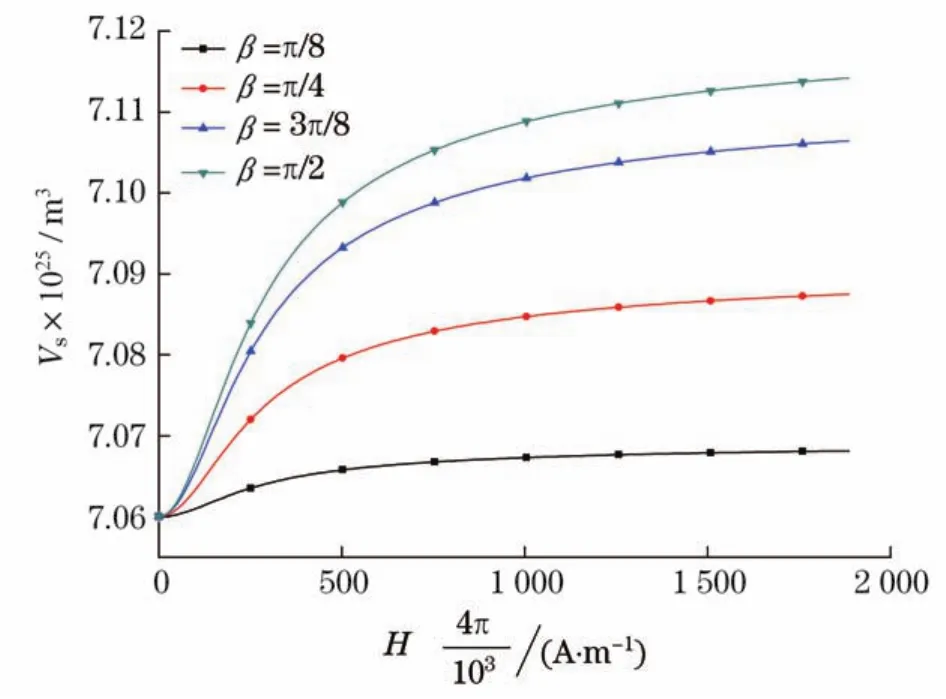
图9 不同外磁场方位角下磁流体的Shliomis体积与外磁场强度的变化关系Fig.9 Shliomis volume of magnetic fluid as a function of magnetic field strength at several azimuthal angles of magnetic field

4 结束语

理论分析了影响磁流体黏度及Shliomis体积的主要因素,并通过数值模拟计算进行了定量的研究.结果表明,磁流体的Shliomis体积随环境温度的增加先迅速减小(接近磁流体熔点温度时),后趋于稳定值(远离磁流体熔点温度时),最后稍微增加;随磁性颗粒浓度的增加而增加;随外磁场强度和方位角的增加而增大.磁流体的Shliomis体积随几类主要参数的变化规律与其黏度随各参数的变化规律类似.因此,黏度对磁流体的Shliomis体积具有直接的、重要的影响.磁流体的Shliomis体积与其场诱导各向异性的形成具有直接的联系,因此,有关研究结果对基于磁流体磁光各向异性的磁光器件设计及相关磁流体的制备具有参考价值.

[1] Rosensweig RE.Ferrohydrodynamics[M].Cambridge: Cambridge University Press,1985.

[2] 卜胜利,纪红柱,于国君,等.基于几何遮蔽效应和法拉第旋光效应耦合的磁流体偏振光透过率[J].光子学报,2012,41(5):614-618.

[3] 卜胜利,陈险峰.纳米磁性液体的分散稳定性分析[J].上海理工大学学报,2008,30(4):335-338.

[4] Candiani A,Argyros A,Leon-Saval S G,et al.A lossbased,magnetic field sensor implemented in a ferrofluid infiltrated microstructured polymer optical fiber[J]. Applied Physics Letters,2014,104(11):111106.

[5] Agruzov P M,Pleshakov I V,Bibik E E,et al. Magneto-optic effects in silica core microstructured fibers with a ferrofluidic cladding[J].Applied Physics Letters,2014,104(7):071108.

[6] Chen S,Fan F,Chang S J,et al.Tunable optical and magneto-optical properties of ferrofluid in the terahertz regime[J].Optics Express,2014,22(6):6313-6321.

[7] Dong S H,Pu S L,Wang H T.Magnetic field sensing based on magnetic-fluid-clad fiber-optic structure with taper-like and lateral-offset fusion splicing[J].Optics Express,2014,22(16):19108-19116.

[8] Pu S L,Dong S H,Huang J.Tunable slow light based on magnetic-fluid-infiltrated photonic crystal waveguides [J].Journal of Optics,2014,16(4):045102.

[9] Shliomis M I.Magnetic fluids[J].Soviet Physics Uspekhi,1974,17(2):153-169.

[10] Shobaki J,Rawwagah F,Abu-Aljarayesh I,et al. Numerical calculation of the temperature variation of the optical anisotropy in magnetic fluids[J].Journal of Magnetism and Magnetic Materials,1996,159(3): 367-374.

[11] Shobaki J,Musameh S,Rawwagah F,et al.Numerical calculation of the magnetodielectric anisotropy effect in magnetic fluids[J].Physical Review B,1996,54 (18):13063-13071.

[12] Odenbach S.Magnetoviscous effects in ferrofluids [M].Germany:Springer,2002.

[13] Shliomis M I.Effective viscosity of magnetic suspensions [J].Soviet Physics Journal of Experimental and Teoretical Physics,1972,34(6):1291-1294.

[14] McTague JP.Magnetoviscosity of magnetic colloids [J].The Journal of Chemical Physics,1969,51(1): 133-136.

[15] Yusuf N,Abu-Aljarayesh I O.Magneto-optical and magneto-dielectric anisotropy effects in magnetic fluids [J].Jordan Journal of Physics,2009,2(1):1-46.

[16] Upadhyay R V,Aswal V K,Desai R.Micro-structural characterisation of water-based magnetic fluid[J]. International Journal of Nanoparticles,2012,5(3): 243-257.

[17] Zu P,Chan CC,Lew W S,et al.Magneto-optical fiber sensor based on magnetic fluid[J].Optics Letters, 2012,37(3):398-400.

[18] Ong R S,Nicholls J A.On the flow of a hydromagnetic fluid near an oscillating flat plate[J].Journal of the Aerospace Sciences,1959,26(5):313-314.

(编辑:石 瑛)

文章编号:1007-6735(2015)05-0419-06 DOI:10.13255/j.cnki.jusst.2015.05.002

Multiparameter-Dependent Shliomis Volume of Magnetic Fluids

PUShengli, WULonglong
(College of Science,University of Shanghai for Science and Technology,Shanghai 200093,China)

According to the analytical expression of Shliomis volume of magnetic fluid,the influence of concentrations of magnetic nanoparticles,ambient temperature and external magnetic field on Shliomis volume were analyzed theoretically and calculated numerically.The results show that Shliomis volume increases with the increase of concentration of magnetic nanoparticles, decreases with the increase of ambient temperature(tends to saturate when the temperature is far beyond the melting point of magnetic fluid).The Shliomis volume of magnetic fluid also depends on the magnetic field’s direction and strength.The viscosity of magnetic fluid is critical to the Shliomis volume.The result is helpful for studying the magnetic moment relaxation of nanoparticles within the magnetic fluid.

magnetic fluid;Shliomis volume;concentration;temperature;magnetic field

O 469

A

2014-09-24

上海市自然科学基金资助项目(13ZR1427400);沪江基金资助项目(B14004)

卜胜利(1978-),男,副教授.研究方向:新型光子学材料及器件.E-mail:shlpu@usst.edu.cn