基于模型相似度拟合的海杂波统计方法
赵荻,孟俊敏,张晰,郎海涛,3*
(1.北京化工大学 应用物理系,北京 100029;2.国家海洋局 第一海洋研究所,山东 青岛 266061;3.海洋遥测工程技术研究中心,山东 青岛 266061)
基于模型相似度拟合的海杂波统计方法
赵荻1,孟俊敏2,张晰2,郎海涛1,3*
(1.北京化工大学 应用物理系,北京 100029;2.国家海洋局 第一海洋研究所,山东 青岛 266061;3.海洋遥测工程技术研究中心,山东 青岛 266061)
本文提出一种基于模型相似度拟合的海杂波统计方法。首先根据合成孔径雷达(SAR)图像计算瑞利分布、对数正态分布、韦布尔分布、K分布、G0分布5种经典的海杂波分布的概率密度函数,然后根据模型间的相似度准则拟合得到新的海杂波分布模型。文章利用四景不同类型的真实SAR数据对算法的拟合性能进行了评价,结果显示利用该算法得到的拟合模型与真实SAR数据的平均Kullback-Leibler距离仅为0.015 84,远优于其他分布模型。基于该拟合模型的恒虚警率舰船检测算法对四景SAR数据的平均检测精度达到95.75%,在控制虚警和漏检方面均优于采用其他模型的同类方法。
海杂波统计模型;恒虚警率;舰船检测;合成孔径雷达
1 引言
星载合成孔径雷达(Satellite SAR)因具有全天时、全天候、大范围的观测能力,而成为海洋监测的有效手段。基于星载SAR图像的舰船检测是海洋监测系统中的重要环节,在海洋交通管理、环境保护、渔业管理、打击非法移民等应用中发挥着重要的作用[1]。
基于海杂波统计分布模型的恒虚警率检测算法,受到广泛的关注和深入研究,是迄今为止发展的最成熟的舰船检测算法,已被应用于很多实际的舰船检测系统中[2]。该方法根据海杂波的概率密度分布(Probability Distribution Function,PDF)计算累积分布密度(Cumulative Distribution Function,CDF),并结合预先设定的恒虚警率(Constant False Alarm Rate,CFAR),自适应的计算检测阈值,将舰船目标从海洋背景中分割出来。
对海杂波进行精确的统计描述是CFAR算法的核心和关键。早期的海杂波统计基于SAR成像相干斑模型,从相干斑的统计特性出发,建立了相干斑幅度服从瑞利分布,强度服从负指数分布的模型[3]。随着SAR成像分辨率的提高,图像中不仅存在相干斑,还存在纹理信息,Ward等证明了二者之间满足乘性关系[4],进而在乘性模型框架下发展了K分布[5—6]、G0分布[7—8]等模型。除了上述基于相干斑先验假设的海杂波统计模型外,还发展了通过对真实SAR图像数据统计建模实验的验证而获得的模型,主要包括对数正态分布[9]、韦布尔分布[10]等模型。近期的文献[11—12]综述了SAR图像统计模型。
受SAR入射角、极化方式不同,以及天气、风速、海况变化等内外因素的影响,海杂波在SAR图像中的统计分布具有较大的差异,可能服从不同的分布模型。因此,利用某一个特定的分布建模不同SAR图像的海杂波是不可行的。即便对于同一景SAR图像,在均匀和不均匀区域,海杂波也可能遵循不同的统计模型。基于这些分析,一些自适应的海杂波建模方法被提出。Qin等[13]利用广义伽玛分布对海杂波进行建模。广义伽玛分布有3个分布参数,分别为尺度参数β,形状参数λ,能量参数ν。Anastassopoulos等[14]证明当分布参数选取特定值时,广义伽玛分布分别退化为瑞利分布(ν=2,λ=1)、指数分布(ν=1,λ=1)、对数正态分布(ν=1,λ→0)、韦布尔分布(λ=1)等形式,因此适用范围更广泛。陈祥等[15]首先根据SAR图像估计各分布的参数,从而得出各自的概率密度函数和累积分布函数。然后使用K-S统计检验量衡量各种统计模型对海杂波直方图的拟合性能,从中选择一种拟合情况最优的统计模型。Blake[16]介绍了一种联合分布模型,首先将同一景SAR图像根据海杂波分布是否均匀划分为多个区域,然后采用不同统计模型统计不同区域的海杂波分布。
本文提出的海杂波统计方法,首先根据具体的SAR图像计算包括瑞利分布、对数正态分布、K分布、韦布尔分布、G0分布在内的5种分布模型,然后根据各分布概率密度函数的相似度,逐点拟合得到全新的概率密度函数,即自适应的SAR图像的海杂波统计模型。与文献[13,15]的方法不同,本文方法得到的模型既不是某个广义模型退化的结果,也不是从各分布中选择一个与实际SAR图像直方图的拟合程度最高的分布,而是由各分布函数拟合出一个全新的分布。与文献[16]相比,本文的方法无需对SAR图像进行均匀/非均匀区域分割,因此更简单易行。
本文内容组织如下:第2部分介绍了本文提出的基于相似度拟合的海杂波统计方法,第3部分使用真实SAR数据,对本文方法得到的海杂波模型的拟合精度和舰船检测性能进行了测试,实验结果表明,与5种经典的海杂波模型相比,本文方法拟合得到的海杂波分布在拟合精度和舰船检测精度上都优于现有的模型。实验也从另一个角度证明了不同的海杂波模型对SAR数据的依赖性。第4部分对全文进行了总结,并介绍了下一步研究设想。
2 基于模型相似度拟合的海杂波统计方法
参考图3a,比较不同海杂波统计模型的概率密度函数与SAR图像的统计直方图可以发现:
(1)尽管没有一种海杂波统计模型能够在幅值/强度全区间完全匹配实际的海杂波分布,但是不同的模型在不同的幅值/强度区间能够较好的匹配实际的海杂波分布。这体现了不同海杂波统计模型的统计互补性。
(2)与实际海杂波匹配较好的幅值/强度区间,通常对应概率密度分布相似度较高的多个统计模型。这体现了不同海杂波统计模型的统计一致性。
基于上述发现,本文提出基于海杂波概率密度分布相似度拟合的海杂波统计方法,具体实现步骤如下:
第一步:输入原始SAR图像,按幅度或者强度值归一化到[0,1]区间。
第二步:利用对数累积量方法(MoLC)[17]分别计算瑞利分布、对数正态分布、韦布尔分布、G0分布、K分布5种模型的参数,得到对应的概率密度函数f(x)。本文采用了各分布概率密度的幅度分布形式,具体的公式如表1所示。

表1 本文采用的5种分布模型(幅度)
第三步:解下述优化问题,根据概率密度函数相似度拟合新的海杂波分布函数
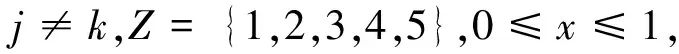
(1)
上述优化问题的本质是在幅度x的分布区间[0,1]内,逐点计算各模型与其他模型间对该点海杂波分布估计的差异性,最终选择与其他模型差异最小的一个,也就是与多数模型相似度最高的一个作为对该点的杂波估计。本文利用模型间概率密度差值的累加值作为相似性评价准则,在具体实现上,采用式(1)的离散化形式:
(2)
式中,N表示对幅值分割的阶数,可根据具体的SAR数据动态范围选择28,216等值。
图3a中黑色实线描绘了对测试图像1(参考表2及图1a)的海杂波拟合的概率密度分布函数。从中可以看出,在不同幅值变化区间,本文方法自适应的择优选取不同的海杂波分布模型对SAR图像海杂波进行建模,拟合得到的概率密度函数最接近真实的海杂波分布(如图3a中背景直方图所示)。本方法本质上是一种自适应的模型选择方法,但与现有的方法存在明显的不同,既不是如文献[13]那样将广义的海杂波模型针对具体SAR图像进行退化,也不是如文献[15]那样根据不同模型与实际海杂波直方图的匹配情况,选择最佳匹配模型,而是根据多个海杂波统计模型的相似度逐点拟合出全新的海杂波分布。本方法也可以如文献[16]那样对图像进行分块处理,但是不需要进行均匀/非均匀区域分割的复杂过程。
3 模型评估与分析
3.1 测试数据
为有效评估本文方法对实际海杂波的统计建模能力,以及基于该模型的CFAR舰船检测算法的性能。利用4景星载SAR图像对方法的拟合性能与检测性能进行了实验验证,并将结果与采用瑞利分布、对数正态分布、韦布尔分布、G0分布、K分布5种经典模型的方法进行了比较。
为了充分验证算法对不同SAR传感器、不同成像模式、不同波段、不同极化方式、不同分辨率、不同海况的适应性,本文选择了具有多样性的SAR数据,这些数据来自于课题组自2010年7月至2012年8月所进行的4次星载SAR舰船探测实验。具体的数据信息及原始SAR图像分别如图1和表2所示,a~d图像信息见表2中1~4。

图1 SAR图像Fig.1 SAR image
表2 SAR图像数据信息
Tab.2 The data information of SAR image

序号日期地点SAR分辨率/m大小/pixel极化波段模式12012-04-28青岛Radarsat⁃281255×1327VV/VHCStandard22011-09-26日照TerraSAR33401×2578HHXStripMap32010-07-18大连COSMO⁃Skymed33290×2647VVXHIMAGE42012-08-16长江口Radarsat⁃211 83660×2728VVCWide
3.2 拟合性能
为评价方法对真实SAR图像海杂波的拟合性能,本文采用K-L距离(Kullback-Leibler)[18]测度对不同分布模型与实际SAR图像海杂波分布的匹配精度进行了评估。假设SAR图像的真实概率分布即图像的直方图分布为p(x),f(x)表示统计模型的分布。对于离散变量xi,统计模型与真实分布之间的K-L距离可以表示为:
(3)
K-L距离又称相对熵,用来衡量两个概率分布的差异性。由式(3)可以看出,当p(x)=f(x)时,DKL=0,也就是说统计模型与真实分布越接近,它们之间的K-L距离越小。图像幅值分割阶数N的选取会对拟合效果产生一定的影响。图2是本文方法采用不同分割阶数对图1a所示的动态范围为[0,28]的SAR图像(即8位SAR数据)的拟合结果。可以看出,拟合性能随着N值的增大而提高,当N值达到SAR数据的最大动态范围时,拟合性能最好。因此本文建议按照SAR数据的动态范围设置分割阶数N选取28,216等值。本文的实验都是针对8位SAR数据进行的测试,因此N均选取28。
表3列出了对4景测试图像,本文方法连同5种统计模型与各图像真实海杂波分布的K-L距离。从表3可以看出,5种经典的海杂波模型对不同的SAR图像建模时表现出了明显的差异性,例如韦布尔分布对图像2和4建模精度很高,G0分布对图像1和3建模精度很高,而K分布对图像2和3建模精度很高,这一结果体现了不同模型对SAR数据的依赖性,与本文之前的分析相符。值得注意的是,本文方法给出的模型,对各幅图像都得到了最高的拟合精度,验证了算法在拟合性能上的优越性。具体的拟合概率密度分布如图3所示。

图2 拟合性能与图像分割阶数的关系Fig.2 The relationship of the fitting performance with segmentation order
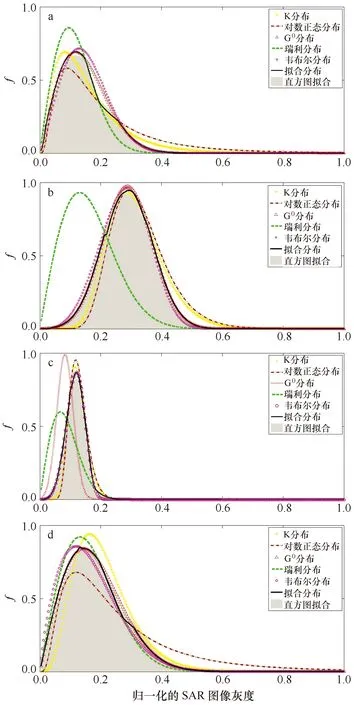
图3 不同分布模型的海杂波直方图拟合, a~d分别为图1中图像a~d直方图拟合Fig.3 The sea clutter histogram fitting of different distribution models, a~d are the histogram fitting of the images a~d in Fig.1, respectively
3.3 检测性能
为了进一步验证本文方法得到的海杂波模型的舰船检测性能,本文采用CFAR方法,对四景测试图像进行舰船检测实验。这里,对本文方法获得的模型及上述5种经典模型均采用一种局部CFAR方法,即将待测SAR图像分割成局部子区域,利用恒虚警率求取每个局部区域的检测阈值,从而检测SAR舰船目标。设海杂波的累积概率密度函数为Fn(x),这里n表示局部子区域数量,n值越大,则检测精度更高,但计算时间相对越长,本方法对每景SAR图像的n值均取4,则局部阈值Tn可以由式(4)得到,对于局部子区域中的幅度值,若大于对应区域的阈值Tn,则判定为舰船目标,否则为海杂波。

表3 各分布与图像直方图的K-L距离
(4)
为了客观评价算法检测效果,对各模型实验均采用了完全相同的实验配置,各测试图像都经过了几何校正、天线方向图校正、陆地掩膜及初步检测后的形态学处理等操作。图像中舰船位置来自于实验时同步获取的AIS信息和专家解译结果。算法性能根据正确检测目标数,漏检目标数,虚警目标数进行评价,参考品质因数FoM指标参数[8],其定义为:
(5)
式中,Ntt为检测结果中正确的检测目标数,Nfa为虚警目标数,Ngt为实际的目标数。
完整的实验结果如表4所示。从中可以看出:对于图像1和3,本文提出的算法相比于其他5种算法,既能有效地控制虚警,又能减少漏检。图像2的海杂波分布较均匀,从检测结果看,6种算法都没有虚警产生,其中,基于K分布、G0分布的CFAR检测算法与本文算法漏检目标数最少,检测精度最高。针对测试图像4中大量舰船目标检测,本文算法相比于对数正态模型及K分布模型来说,能有效地减少漏检,同时相比于其他3种算法又能够更好地控制虚警。综上所述,基于本文方法拟合海杂波模型的CFAR算法相比于其他模型,在不同SAR传感器,不同图像分辨率,不同海况,不同舰船密集度情况下,都能够有效地减少漏检与虚警,实现高精度的舰船目标检测。
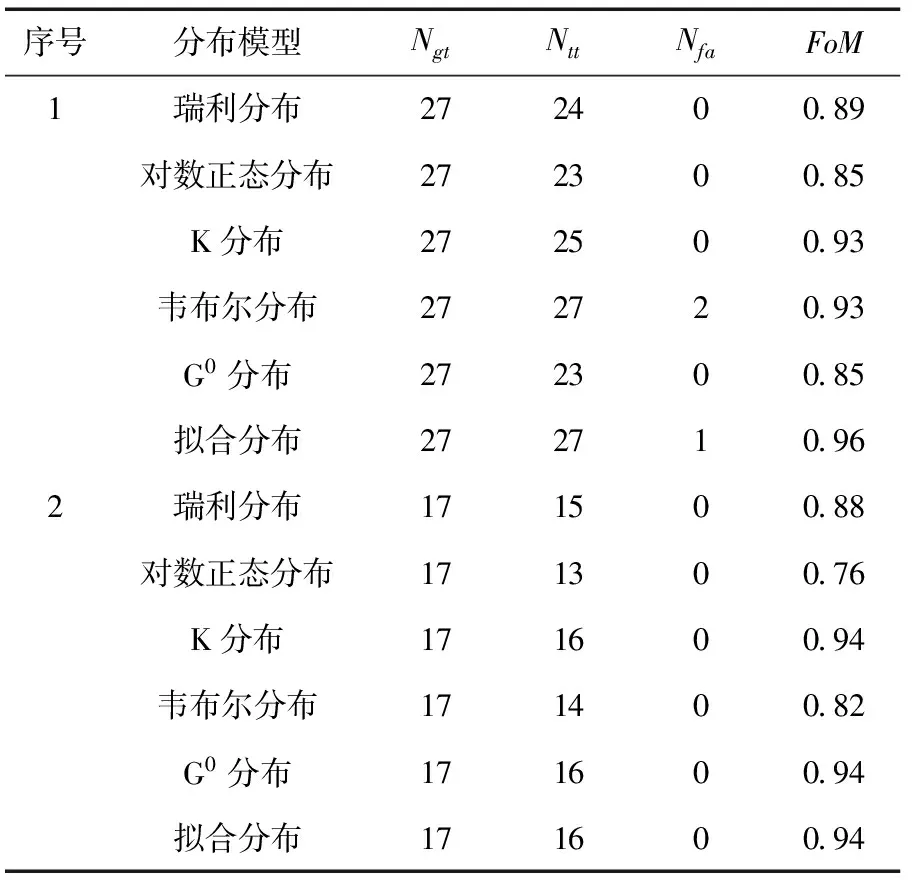
表4 各种算法对表1中4景SAR图像检测结果
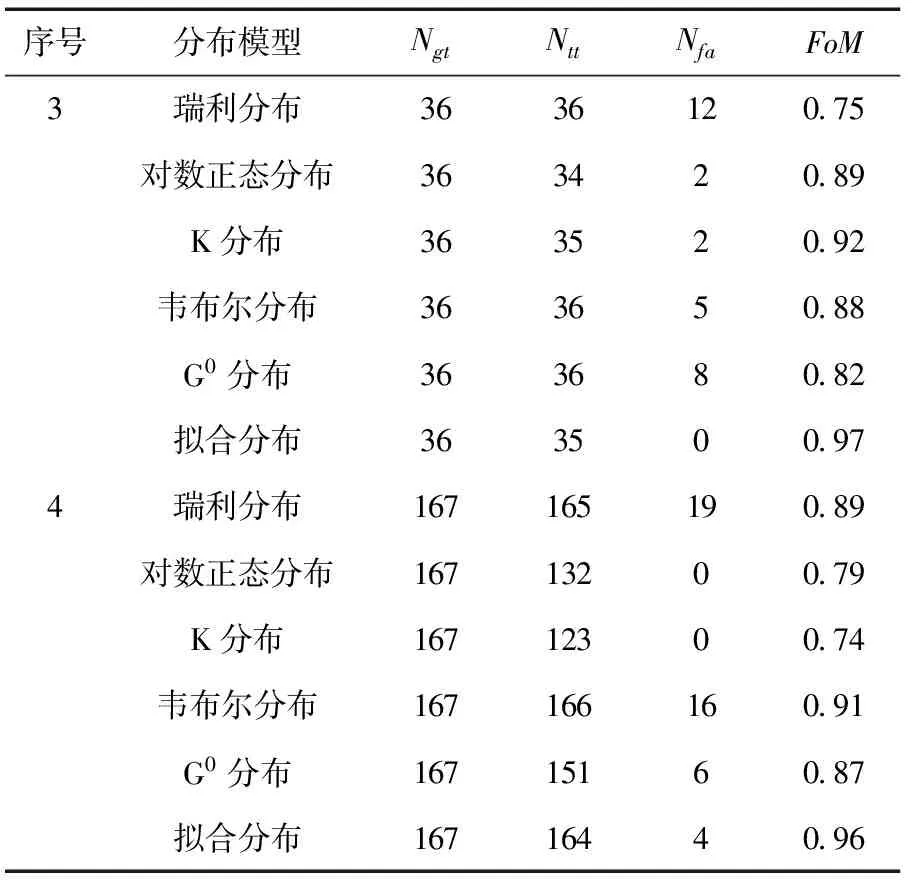
续表4
为了更直观的给出检测结果,图4绘出了基于不同海杂波模型的CFAR算法对测试图像4的检测结果,图中矩形框内为正确检测的目标,椭圆形框内为虚警目标,三角形框内为漏检目标。基于本文方法拟合海杂波模型的CFAR检测算法对其他3幅测试图像的检测结果如图5所示。
4 结论与展望
本文的实验结果(参考表3及对其的分析)进一步证明了没有一种单一的海杂波统计模型能够对受不同内外因素影响的SAR图像进行精确的建模,必须根据实际的SAR图像自适应的构建海杂波模型。
与文献[13,15—16]等提出的自适应海杂波建模方法不同,本文提出的基于模型相似度拟合的海杂波统计方法根据5种经典模型重新拟合得到全新的海杂波模型,而不是从中选择一个与实际SAR图像的全部或者部分区域拟合最好的模型。通过拟合性能和检测性能两方面的实验测试表明,本方法明显优于上述5种经典模型。
本文的方法将基于相干斑的先验假设统计模型(瑞利分布、K分布),与基于实验数据的经验分布模型(对数正态分布、韦布尔分布、G0分布)相融合,拟合得到的模型虽然没有先验假设统计模型那么强的物理意义,也没有经验分布模型那么严格的数学意义,但是由于其充分利用了各经典模型间的互补性,因此得到了良好的拟合效果。
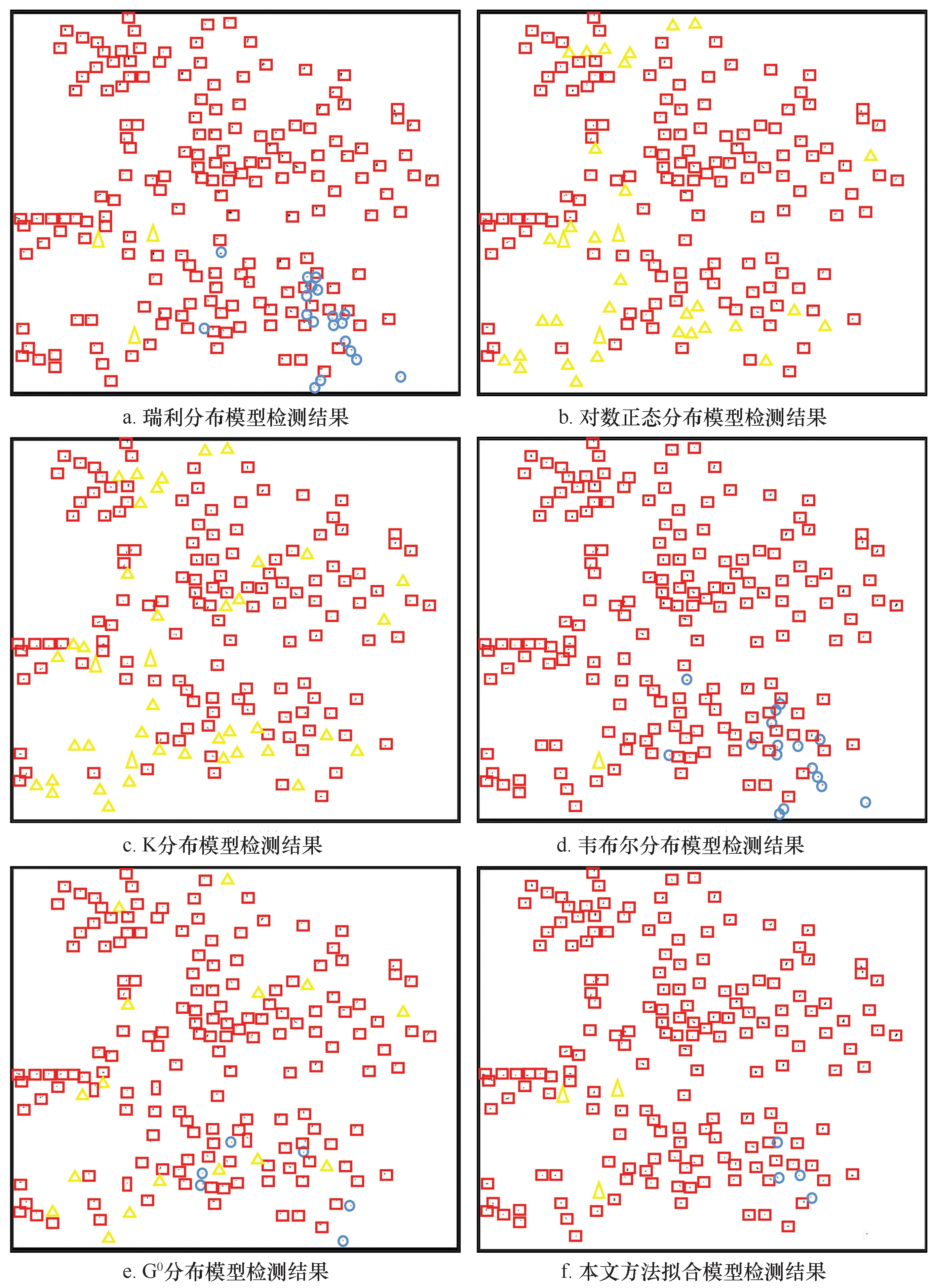
图4 基于不同海杂波模型的CFAR算法对测试图像4的检测结果Fig.4 The detection results for image 4 by CFAR algorithms based on different sea clutter models

图5 本文方法拟合模型对测试图像1~3的检测结果Fig.5 The detection results for images 1~3 by the method proposed in this paper
在今后的工作中,我们将进一步研究将该拟合模型与不同的CFAR舰船检测算法相结合,提高舰船检测精度的方法。
致谢:感谢审稿人在实验结果表达方面提出的宝贵建议!
[1] Brusch S,Lehner S,Fritz T,et al. Ship surveillance with TerraSAR-X[J]. IEEE Transactions on Geoscience and Remote Sensing,2011,49(3):1092-1103.
[2] Crisp D J. The state-of-the-art in ship detection in synthetic aperture radar imagery[R]. Defence Science And Technology Organisation Salisbury (Australia) Info Sciences Lab,2004.
[3] Oliver C,Quegan S. Understanding synthetic aperture radar images[M]. Sci Tech Publishing,2004.
[4] Ward K D. Compound representation of high resolution sea clutter[J]. Electronics Letters,1981,17(16): 561-563.
[5] Ji Y,Zhang J,Meng J,et al. A new CFAR ship target detection method in SAR imagery[J]. Acta Oceanologica Sinica,2010,29(1): 12-16.
[6] Jakeman E,Pusey P N. A model for non-Rayleigh sea echo[J]. IEEE Transactions on Antennas and Propagation,1976,24(6): 806-814.
[7] Frery A C,Muller H J,Yanasse C C F,et al. A Model for Extremely Heterogeneous Clutter[J]. IEEE Transactions on Geoscience and Remote Sensing,1997,35(3): 648-659.
[8] 鲁统臻,张杰,纪永刚,等. 基于G0分布的高海况SAR船只目标检测方法[J]. 海洋科学进展,2011,29(2):186-195.
Lu Tongzhen,Zhang Jie,Ji Yonggang,et al. Ship target detection algorithm based on G0distribution for SAR images under rough sea conditions[J].Advances in Marine Science,2011,29(2):186-195.
[9] Szajnowski W. Estimators of log-normal distribution parameters[J]. IEEE Transaction on Aerospace Electronic Systems,1977,13(5): 533-536.
[10] Tsagaris V,Vozikis G. Ship detection modules based on ASAR and terassar data for Greek areas of interest[C]//IEEE 2nd International Conference on Space Technology (ICST),2011 :1-4.
[11] 李永晨,刘浏. SAR图像统计模型综述[J]. 计算机工程与应用,2013,49(13):180-186.
Li Yongchen,Liu Liu. Review of statistical model of SAR image[J]. Computer Engineering and Applications,2013,49(13):180-186.
[12] Gao G. Statistical modeling of SAR images: A survey[J]. Sensors,2010,10(1):775-795.
[13] Qin X X,Zhou S L,Zou H X,et al. A CFAR detection algorithm for generalized gamma distributed background in high-resolution SAR images[J]. Geoscience and Remote Sensing Letters,IEEE,2013,10(4): 806-810.
[14] Anastassopoulos V,Lampropoulos G A,Drosopoulos A,et al. High resolution radar clutter statistics[J].IEEE Transactions on Aerospace and Electronic Systems,1999,35(1):43-60.
[15] 陈祥,孙俊,尹奎英,等. 基于CFAR级联的SAR图像舰船目标检测算法[J]. 现代雷达,2012,34(9): 50-55.
Chen Xiang,Sun Jun,Yin Kuiying,et al. An algorithm of ship target detection in SAR images based on cascaded CFAR[J]. Modern Radar,2012,34(9): 50-55.
[16] Blake A P. High resolution SAR clutter textural analysis and simulation[J]. SPIE,1995,2584:101-108.
[17] Li H C,Hong W,Wu Y R,et al. On the empirical-statistical modeling of SAR images with generalized gamma distribution[J]. Selected Topics in Signal Processing,IEEE,2011,5(3): 386-397.
[18] Burnham K P,Anderson D R. Model selection and multi-model inference: a practical information-theoretic approach[M].New York: Springer,2002.
Sea clutter statistics based on similarity fitting of classical models
Zhao Di1,Meng Junmin2,Zhang Xi2,Lang Haitao1,3
(1.DepartmentofAppliedPhysics,BeijingUniversityofChemicalTechnology,Beijing100029,China; 2.TheFirstInstituteofOceanography,StateOceanicAdministration,Qingdao266061,China; 3.EngineeringResearchCenterforMarineTelemetry,StateOceanicAdministration&ChinaNationalSpaceAdministration,Qingdao266061,China)
A sea clutter statistical method based on similarity fitting is proposed in this paper. We first estimate five classical probability density functions of the sea clutter distribution in synthetic aperture radar (SAR) imagery,which include Rayleigh distribution,lognormal distribution,Weibull distribution,K distribution and G0distribution. Thereafter,we fit all these five models to a new sea clutter distribution by an optimization method based on a similarity criterion. In the experiment,we evaluate the fitting precision based on the Kullback-Leibler distance using four SAR images. The results show the K-L distance between the fitting model and observations is only 0.015 84 when using the proposed algorithm. The fitting model is concluded to be superior to five classical distribution models. When we conduct ship detection using the fitting model and CFAR algorithm,the mean detection accuracy can reach up to 95.75%.
sea clutter statistical model; constant false alarm rate (CFAR); ship detection,synthetic aperture radar (SAR)
10.3969/j.issn.0253-4193.2015.05.011
2014-02-21;
2014-06-16。
海洋公益性行业科研专项经费项目(200905029,201505002-1);中央高校基本科研业务费专项资金北京化工大学(JD1414)。
赵荻(1989—),女,天津市人,主要从事SAR图像解译的研究。E-mail:zhaodi233@163.com
*通信作者:郎海涛(1978—),男,黑龙江省人,副教授,博士,从事模式识别与遥感图像解译的研究。E-mail:langht@mail.buct.edu.cn
TN957.51;TP751.1
A
0253-4193(2015)05-0112-09
赵荻,孟俊敏,张晰,等. 基于模型相似度拟合的海杂波统计方法[J]. 海洋学报,2015,37(5):112-120,
Zhao Di,Meng Junmin,Zhang Xi,et al. Sea clutter statistics based on similarity fitting of classical models[J]. Haiyang Xuebao,2015,37(5):112-120,doi:10.3969/j.issn.0253-4193.2015.05.011

