顾及姿态角的多波束声线精确跟踪方法

何林帮，赵建虎，张红梅，王 晓，严 俊

（1.武汉大学测绘学院，湖北武汉430079；2.武汉大学动力与机械学院自动化系，湖北武汉430072）

顾及姿态角的多波束声线精确跟踪方法

何林帮1，赵建虎1，张红梅2，王 晓1，严 俊1

（1.武汉大学测绘学院，湖北武汉430079；2.武汉大学动力与机械学院自动化系，湖北武汉430072）

传统声线跟踪方法中波束初始入射角的计算采用理想状态下多波束提供的波束分配角，未顾及或未完全顾及船体姿态角的影响进而导致波束海底投射点归位计算带入显著性误差问题。针对此问提出了一种顾及姿态角影响的声线精确跟踪方法，该方法通过研究船体姿态影响下的多波束换能器状态，给出了波束声线实际传播面，并推导出了传播面内波束声线的实际初始入射角，结合声速剖面，最终根据常梯度声线跟踪得到了准确的测深点三维坐标。通过实验比较传统声线跟踪方法和精确声线跟踪方法计算波束在海底投射点的坐标精度，验证了精确声线跟踪方法克服了传统声线跟踪的不足，显著地提高了多波束测深的精度。

多波束测深系统；波束脚印；初始入射角；姿态角；常梯度声线跟踪

随着海洋资源开发的不断推进，海底勘探作为海洋资源开发的基础性工作，且测深工作在海底油气和矿产资源开发、海底电缆铺设、河道清淤、工程建设方案选取等工程应用方面发挥着重要的作用，测深精度也直接影响着工程应用的效果。在多波束测深中，每个波束在海底投射点的坐标均基于一定的声线跟踪模型获得的，声线跟踪精度直接影响着多波束的测深精度［1］。实际数据处理发现，声线跟踪常会带来一些测深假象，并导致海底地形异常［2］。根据声线跟踪原理，影响声线跟踪精度的主要因素有声速剖面误差、波束初始入射角误差和声线跟踪模型误差。声速剖面误差是影响测深精度的第一误差源，包括声速测量误差和声速代表性误差，可以借助高精度声速剖面仪和施测一定密度的声速剖面来消除［3⁃4］；基于层内常梯度的声线跟踪方法，由于假设与实际一致，具有较高的声线跟踪精度［4］。实际应用中发现，消除了上述2个因素影响后，测深结果仍不理想，尤其是在深水区多波束测量中［3⁃5］。分析认为，主要由于目前声线跟踪方法中的波束初始入射角计算未顾及或未完全顾及船姿因素所致。目前，声线跟踪中波束初始入射角的获取有2种方式：1）直接来自换能器提供的各波束分配角［4］；2）仅顾及了横摇角，即波束初始入射角为波束分配角与横摇角之和［3］。以上2种初始入射角获取方法均基于一个假设，即多波束Ping测深断面与测量船航迹方向正交，而实际多波束换能器在横摇、纵摇姿态角作用下，Ping测深断面与航迹方向已不再正交，而前者未顾及这一影响，后者虽顾及了横摇影响，但忽视了纵摇；此外，在对姿态影响的处理方面，2种方法均先通过声线跟踪获得波束点坐标，尔后再借助姿态角构建旋转矩阵进行强制旋转变换，获得波束海底测深点在理想船体坐标系下的坐标。不同的是，前者借助纵摇、横摇角构建的旋转矩阵来实施变换，而后者仅借助纵摇角构建的旋转矩阵进行变化。综上可知，现有波束测深点位计算均与实际存在着一定的误差，也因此导致了前述测深假象，且随着水深的增加，其影响愈加显著。因此，本文提出了一种精确的声线跟踪方法，以期通过研究姿态对Ping测深断面的影响，获得声线在空间的实际传播路径和顾及姿态角的实际波束初始入射角，从而实现波束测深点位置的正确计算，提高多波束测深精度。

1 顾及姿态角的声线跟踪方法

1.1 常梯度声线跟踪方法及波束初始入射角的影响分析

海水中声速与海水温度、盐度和静压力相关，随着深度的变化而变化［6］。由于很难获得声速随深度变化的函数，通常只能借助声速剖面仪获得一定深度间隔的声速剖面，并根据声速变化，借助Snell法则，沿声线跟踪，获得波束海底投射点在船体坐标系下的坐标［7⁃8］。在每个水层中，由于只知道该层上界和下界声速，因此通常假设声速在该层以常梯度g传播，采用类似处理方法处理其他各水层，并沿着声线跟踪到海底，即实现常梯度声线跟踪和波束海底坐标计算［9］。

假设声线从换能器发射，经过N个水层，每个水层上界Zi声速为Ci，下界Zi+1声速为Ci+1，层内声速以常梯度gi变化，则层i内声速函数为

如图1声线跟踪示意图所示，在常梯度gi声速变化下，声线在第i层内的传播轨迹为一连续的、带有一定曲率、半径为Ri的弧段［4］，若Snell常数为p，则Ri为

图1 常梯度声线跟踪示意图Fig.1 Schematic diagram of constant⁃gradient sound ray tracking

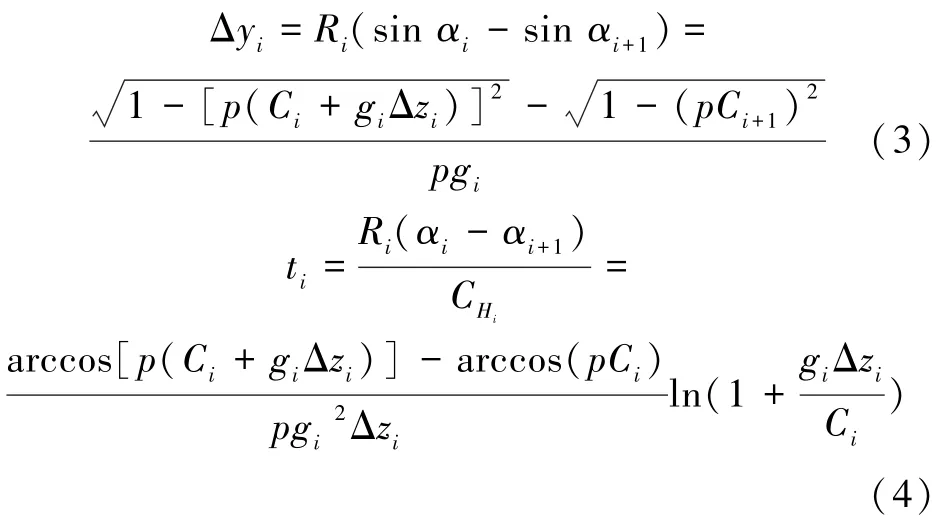
在分层声线跟踪时，除了计算整层的垂直位移、水平位移和传播时间外，还需要依据传播剩余时间计算剩余层的垂直位移和水平位移。假设声线在第i层内传播时，声线在该层内r点处（如图1）结束，此时剩余时间tr等于波束单程旅行时间tall减去第i层以前累计的传播时间，则声线在剩余层内的垂直位移Δzr和水平位移Δyr为

则声线传播总的垂直位移z和水平位移y为

姿态角（横摇角r和纵摇角p）改变了换能器的理想发射状态，为顾及该影响，传统数据处理方法借助换能器的波束分配角完成上述声线跟踪后得到波束坐标（x，y，z），且根据横摇角r和纵摇角p波束坐标的影响进行了坐标旋转变换，从而获得了波束在船体坐标系下的坐标（x'，y'，z'）［10］。

以上传统数据处理方法存在如下问题：

1）认为声线传播面，也即Ping断面，与航向方向正交，而实际声线传播面并非如此。

2）受姿态因素影响，换能器的理想状态已发生变化，实际波束初始入射角不再是理想状态下的波束分配角，而是受姿态角影响的入射角。根据Snell法则sin θ0／C0＝sin θ1／C1＝p，若初始入射角为θ0，其误差为dθ0，则有［11］

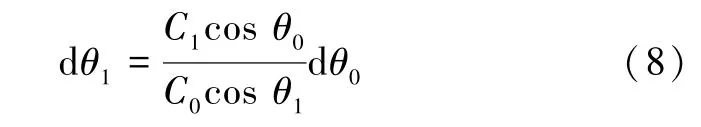
式（8）表明，初始入射角存在误差dθ0时，会给下层入射角θ1产生dθ1的误差。由于采取分层跟踪处理，也会进一步影响后续层的折射角θi，并给最终测深点坐标计算带来系统性误差。

3）上述对波束声线先跟踪后旋转的处理方法，实际是将理想状态下的波束测深点旋转到实际的过程，由于1）、2）两方面的影响，这种旋转变换只能给测深点位坐标计算带来新的误差。

以上问题表明，在声速误差和声线跟踪模型正确的情况下，寻找顾及姿态影响的实际声线传播面及正确的初始入射角是实现波束点位坐标精确计算的关键。为此，下面研究给出一种顾及姿态影响下的波束初始入射角的精确计算方法，从而实现测深点坐标精确跟踪计算。

1.2 顾及姿态的波束初始入射角计算

由于船体坐标系的中心通常是以换能器为中心，因此以换能器理想水平状态作为基准面来分析船体姿态对波束初始入射角的影响，如图2所示的换能器基阵坐标系中，水平状态的换能器基准面位于OABC平面内，O为换能器中心，OA为基准面纵轴正方向，OC为基准面横轴正方向。设OA长度为a，OC长度为c，A、B两点的坐标分别为（a，0，0）和（0，c，0）。在某一姿态（横摇、纵摇角分别为r和p）影响下基准面变化为OA1B1C1，即基阵面由水平先绕OX轴旋转角度α（α≠r），再绕OY轴旋转角度β形成。A点、C点经过两次旋转后分别转到A1和C1位置，A1、C1两点在水平面OXY上的投影分别为A2和C2。在此状态下，OA1与水平面夹角∠A1OA2即为纵摇角p，OC1与水平面夹角∠C1OC2即为横摇角r。根据纵摇角、横摇角和旋转角定义，r和α符号一致，p和β符号一致。

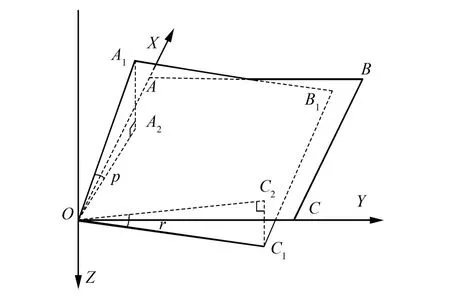
图2 换能器基阵旋转角度模型Fig.2 Transducer array rotation model

由以上过程可知，基准面OABC经过α和β两次旋转得到OA1B1C1，则

则旋转后A1点坐标为

由式（10）得到旋转后A1点坐标再根据三角形正弦定理可计算出基阵面的纵摇角p（即∠A1OA2）：

式中：ZA1为A1点在Z轴上的坐标，根据β与p符号一致可得

类似地，由式（11）得到旋转后C1点坐标再根据三角形正弦定理可计算出基阵面的横摇角r（即∠C1OC2）：

式中：ZC1为C1点在Z轴上的坐标，r和α符号一致，并将β＝p代入式（14）得

由式（13）和（16）可知，在旋转变换中，绕OY轴旋转角β等于纵摇角p，而绕OX轴旋转角α并不等于横摇角r。因此，在目前较为精细的声线跟踪计算中，即使顾及姿态影响，定义初始入射角为θ0+r显然是不正确的。

为了得到姿态（r、p）影响下真实的波束入射角，下面推导实际波束初始入射角θ0'的计算模型。

由以上推导可知，实际声线可由理想状态下的声线经α、β旋转变换r后得到。设理想状态下，第i个波束分配初始入射角为θi，在不失精度情况下，假设经历第一个水层以常声速传播，传播距离为Ri，则波束在第一水层下界的落点Pi坐标为（0，Risin θi，Ricos θi），而在姿态影响下的实际坐标（xi，yi，zi）为

式（17）可由图3解释。假设换能器基阵水平时，第i号波束的波束角度为θi，斜距为R，则点A坐标为（0，Risin θi，Ricos θi），换能器基阵在横摇r和纵摇p的影响下，A点旋转到了B点，第i号波束的实际入射角度为（即∠BOD），定义经旋转后第i号波束的水平角度φi＝∠BDE，即为波束横距BD与OY轴的夹角，其表达式为

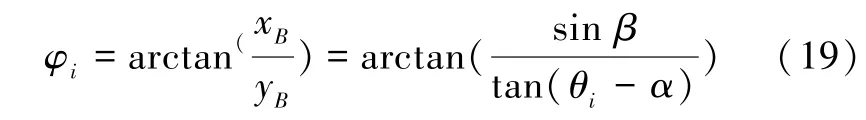
图3 波束点空间旋转示意图Fig.3 Schematic diagram of footprint rotation

由式（18）可获得姿态影响下的波束实际初始入射角，并用于后续声线跟踪。

2 声线跟踪及波束测深点归位计算流程

波束测深点在地理坐标系下的坐标可通过如下过程来获得：

1）波束实际初始入射角计算。由式（13）和式（16）得到换能器基阵面的实际旋转角α和β，并由式（18）得到波束的实际初始入射角

2）常梯度声线跟踪。借助实际声速剖面、1）中获得的波束实际初始入射角以及波束传播时间t，并根据式（1）～（6）进行声线跟踪，获得波束在理想换能器坐标系下坐标（x，y，z）。

3）波束传播垂面与理想状态换能器坐标系XOZ面的二面角Ab计算：

4）波束测深点地理坐标计算［12］

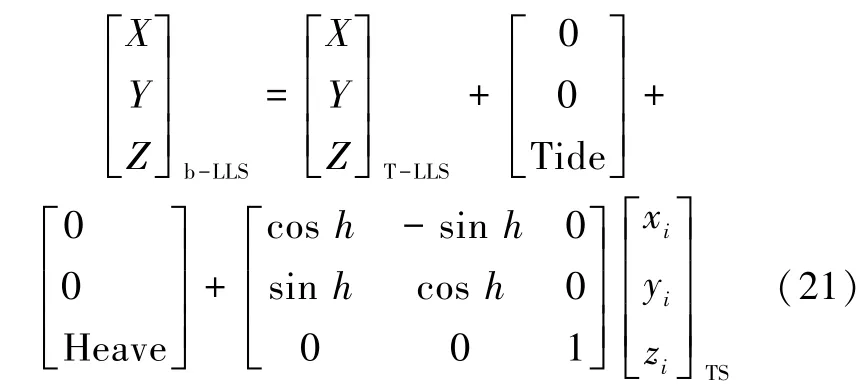
式中：下角b⁃LLS为地理坐标系下的波束测深点坐标，T⁃LLS为由GPS提供的换能器中心地理坐标，TS为船体坐标系下的波束测深点坐标；h为波束垂面方位角，由罗经提供的航向角为A，则h为

3 实验与分析

为检验上述方法的正确性，本实验运用常梯度声线跟踪方法结合声线精确归位模型对胶州湾测深数据进行了处理，本次实验的数据是应用EM3000多波束测深仪器采集的，作业频率为300 kHz，波束角为1.5°× 1.5°，127个波束，波束间隔为0.9°。胶州湾测深实验区的水深在30～50 m范围。通过实验分析本文的声线精确跟踪方法与传统方法的差异，并分析这两种数据处理方法下的测深精度。

选择重叠率达50%左右的两条相邻条带以及一条中央波束近似垂直前两条的条带，由于多波束中央波束相对于边缘波束受姿态影响小得多，在声速剖面正确情况下可视为实际深度，因此以第3个条带的中央波束作为检测线（如图4所示），作为其他2个条带所对应平面位置测深点深度的精度评估。对这3个条带数据分别采用本文的精确归位模型和传统方法进行处理，获得各波束测深点在地理坐标系下的三维坐标。在两条相邻条带中，分别经过X轴和Y轴坐标内查得出检测线所在平面位置的波束测深点水深，以检测线的中央波束实测深度为参考，可评估受声线跟踪影响较大、经本文方法和传统方法分别处理后的水深精度，进而实现对给出的声线精确跟踪方法的正确性评估。

若公共覆盖区某点P的声线跟踪深度为Z，对应平面位置检测线中央波束深度为Z0，则声线跟踪深度的相对精度X为

图4 条带与检测线交叉示意图Fig.4 Schematic diagram of the strip is crossing with detection line

在图4中，右侧条带为第1个条带，左侧条带为第2个条带，横向中间线为第3个条带的中央波束（检测线）。第1个条带与检测线有18个交叉点，第2个条带有40个交叉点，图5和图6分别为本文方法、传统声线跟踪方法计算所得第1个条带和第2个条带与检测线中央波束交叉点的深度精度。可以看出：在第1个条带中，本文给出声线跟踪方法计算的波束深度相对误差在1%之内，而传统方法有50%左右在1%之内，最大的相对误差在1.6%左右；在第2个条带中，本文给出的声线跟踪方法计算的波束深度相对误差也控制在1%之内，而传统方法则处于0.5%～2.7%。

基于本文给出的声线跟踪方法计算所得的波束测深点深度相对误差较小，而应用传统方法处理则存在较大的波动，分析认为前者已全面考虑了姿态角对波束初始入射角的影响，而后者未完全顾及船体姿态的影响，因此会随着船体姿态的变化在不同条带中产生较大的测深误差。

图5 两种声线跟踪方法在条带1所得深度相对误差分布Fig.5 Relative depth errors of two kinds of sound ray tracing at swath 1

图6 两种声线跟踪方法在条带2所得深度相对误差分布Fig.6 Relative depth errors of two kinds of sound ray tracing at swath 2

由图5和图6可以看出，尽管顾及了姿态角的影响，本文给出的声线精确跟踪方法得到的波束测深点深度相对误差仍出现所谓的“笑脸”现象，分析认为尽管采用了测量位置的声速剖面和消除了姿态对波束初始入射角的影响，但波束测深点深度跟踪精度仍会受声速剖面测量误差影响以及其他影响因素的残余误差影响。尽管如此，仍达到了相对测深误差控制在1%范围内的精度，满足了IHO S⁃44标准，远高于传统声线跟踪方法，表明了本文提出的声线精确跟踪方法的正确性。

4 结束语

本文提出的顾及船体姿态角的声线跟踪模型，首先精确地计算出多波束波束的初始入射角，然后根据层内常声速声线跟踪模型计算出波束在海底的投射点坐标。通过实验，利用检测线的平面位置内插得到其他两个相邻条带中与检测线波束脚印相同位置的深度，再计算内插波束点的深度相对误差，实验表明提出的精确声线跟踪方法相对于传统声线跟踪方法，显著地提高了波束测深点深度的计算精度，满足了IHO-44精度要求，对多波束高精度测深具有更好的参考性和实用意义。

［1］CHRISTIAN D M，MARTIN C K.Bathymetric artifacts in sea beam data：how to recongnize them and what causes them［J］.Journal of Geophysical Research，1986，91（B3）：3407⁃3424.

［2］EDOUARD K.A new method for the removal of refraction artifacts in multibeam echosounder systems［D］.New Bruns⁃wick：University of New Brunswick，2000：35⁃60.

［3］DIMITRI A，CHRISTIAN D M.Adaptive noise canceling ap⁃plied to sea beam sideloe interference rejection［J］.IEEE Journal of Oceanic Engineering，1988，13（2）：70⁃76.

［4］赵建虎，刘经南.多波束测深及图像数据处理［M］.武汉：武汉大学出版社，2008：125⁃127.

［5］CHAPPELL D J，GIANI S，TANNER G.Dynamical energy analysis for built⁃up acoustic systems at high frequencies［J］.Journal of Acoustical Society of America，2011，130（3）：1420⁃1429.

［6］刘伯胜，雷家.水声学原理［M］.哈尔滨：哈尔滨工程大学出版社，1993：23.

［7］THOMAS E B.Geometrically derived ray⁃theory results and direct verification of the Pekeris solution for unbounded con⁃stant⁃gradient media［J］.IEEE Journal of Oceanic Engineer⁃ing，2012，37（2）：244⁃254.

［8］HANAKO O，KAZUYOSHI M，TOSHIAKI N.Reciprocal sound propagation experiment in very shallow water area of Hashirimizu port［J］.Japanese Journal of Applied Phys⁃ics，2010（49）：151⁃156.

［9］HAMID R，HADI J R.Target localization and tracking for an isogradient sound speed profile［J］.IEEE Transactions on Signal Processing，2013，61（6）：1434⁃1446.

［10］MCCAFFREY E K.A review of the bathymetric swath sur⁃vey system［J］.International Hydrographic Review，1981，VIII（1）：19⁃27.

［11］陈非凡.多波束条带测深仪的动态测量误差评估［J］.海洋技术，1999，18（1）：41⁃45.

CHEN Feifan.Estimation of dynamic measuring error for multibeam swath bathymeter［J］.Journal of Ocean Tech⁃nology，1998，18（1）：41⁃45.

［12］赵建虎，刘经南.多波束测深系统的归位问题研究［J］.海洋测绘，2003，23（1）：6⁃8.

ZHAO Jianhu，LIU Jingnan.Problems on conformity to the re⁃al sounding points from the multi⁃beam sounding system［J］.Hydrographic Surveying and Charting，2003，23（1）：6⁃8.

A precise multibeam sound ray tracking method taking into account the attitude angle

HE Linbang1，ZHAO Jianhu1，ZHANG Hongmei2，WANG Xiao1，YAN Jun1
（1.School of Geodesy and Geomatics，Wuhan University，Wuhan 430079，China；2.School of Power and Mechanical Engineering，Wuhan University，Wuhan 430072，China）

The assigned beam initial incident angle provided by MBS（multibeam bathymetry system）is adopted by the traditional sound ray tracking method regarding the vessel in the horizontal status，which ignores or does not consider completely the impacts of vessel attitude angles，and lead obvious error to the determination of beam foot⁃print position.Aiming at the problem.In order to reduce this kind of significant error，an accurate method for sound ray tracking，which considers vessel attitude angles are put forward in this paper.In the proposed method，the actu⁃al propagation profile is given by means of studying the actual status of MBS transducer impacted by vessel attitude and the actual initial incidence angle of MBS beam is derived by the calculation model.By integrating the sound ve⁃locity profile，the accurate positioning of beam footprint on seabed is achieved by constant⁃gradient sound ray track⁃ing method.By comparing the beam footprint coordinate precision calculated by traditional sound ray tracking meth⁃od and the precise method of sound ray tracking in experiment，a conclusion can be drawn that the precise method of sound ray tracking can overcome the deficiency of the traditional sound ray tracking.This improves significantly the precision for multi⁃beam bathymetry

multibeam bathymetric system（MBS）；beam footprint；initial incident angle of beam；attitude angle；constant⁃gradient sound ray tracking

10.3969／j.issn.1006⁃7043.201310060

P229

A

1006⁃7043（2015）01⁃0046⁃05

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006⁃7043.201310060.html

2013⁃10⁃21.网络出版时间：2014⁃11⁃07.

国家自然科学基金资助项目（41176068，0976061，40776048，41376109）.

何林帮（1981⁃），男，博士研究生；

赵建虎（1970⁃），男，教授，博士生导师.

何林帮，E⁃mail：whuhlb＠163.com.