一种稀疏度自适应的网络流量矩阵测量方法

杨京礼，崔 征，魏长安，姜守达

（哈尔滨工业大学自动化测试与控制系，150080哈尔滨）

一种稀疏度自适应的网络流量矩阵测量方法

杨京礼，崔 征，魏长安，姜守达

（哈尔滨工业大学自动化测试与控制系，150080哈尔滨）

为提高网络流量矩阵测量的精度，在压缩感知框架下提出一种稀疏度自适应的网络流量矩阵测量方法.通过对网络流量矩阵的主成分分析及奇异值归一化处理寻找信号支撑集选择的判定阈值，利用网络流量矩阵重构过程中的残差L2范数匹配计算各测量时间点上网络流量矩阵的稀疏度，减小由于网络流量矩阵近似稀疏表示以及稀疏度选择不准确造成的测量误差.仿真实验结果表明：所提出的方法与现有方法相比能够获得更小的空间相对误差和时间相对误差.通过稀疏度自适应选择方法，能够有效提高网络流量矩阵的测量精度.

网络测量；网络层析成像；流量矩阵；压缩感知；正交匹配追踪

网络流量矩阵（traffic matrix）作为描述网络中源节点和目的节点之间流量信息（origin destination flow，OD流）的参数，是互联网管理和优化的重要依据［1-2］.随着网络朝着非协作和基于边缘控制的方向演变，传统的直接测量方法不能完全满足网络流量矩阵测量的需求，亟待引进新的测量方法.网络层析成像（network tomography，NT）［3-4］将医学上的计算机层析成像技术引入到网络测量中，在没有内部节点协作的条件下进行端到端的测量，通过网络边界的信息来推断网络链路级性能参数.

目前，现有的基于网络层析成像技术的网络流量矩阵估计方法主要包括基于先验模型［5-8］和无先验模型等［9-13］两类.基于先验模型的网络流量矩阵估计方法计算简单快捷，但该类方法采用的已知概率分布模型［5-8］难以准确反映网络流量矩阵的变化规律，容易造成较大的估计误差.文献［9］提出的线性规划方法以目标函数代替先验模型，解决先验模型难以描述网络流量矩阵规律的问题，但目标函数的选择成为影响该方法的瓶颈问题.文献［10］使用主成分分析将N个流量矩阵的估计问题转换为K（K＜＜N）个最重要特征流的计算问题.该方法在计算过程中会删除特征值较小的特征流向量，造成后续流量矩阵计算过程中出现误差.文献［11］采用递归神经网络对网络流量矩阵进行追踪，但该方法需要较长的时间对神经网络进行训练，因此不适合互联网实时流量矩阵测量的需求.

文献［12-13］提出了基于压缩感知技术的CS-OMP算法，通过矩阵奇异值分解（singular value decomposition，SVD）建立网络流量矩阵的近似稀疏表示，应用正交匹配追踪算法（orthogonal matching pursuit，OMP）完成网络流量矩阵的重构计算.该算法的网络流量矩阵计算精度与预先选择的稀疏度有很强的关联性，当稀疏度取值过小或过大时都会造成较大的测量误差.

为提高网络层析成像技术下流量矩阵测量的精度，本文在压缩感知框架下提出了一种稀疏度自适应的网络流量矩阵测量方法.通过对网络流量矩阵数据主成分分析中奇异值的归一化处理寻找信号支撑集选择的判定阈值，利用正交匹配追踪数据恢复中残差范数匹配所有测量时间点上网络流量矩阵的稀疏度，降低网络流量矩阵近似稀疏表示造成的测量误差.

1 模型与估计

1.1 网络模型

在网络层析成像框架下进行流量矩阵估计时，链路流量表示相邻两节点间链路上传输的数据量大小，是各网络OD流在链路上的聚合.设为在测量时间点q上的链路流量，M为网络链路数量；为当前测量时间点上的网络流量矩阵；N为网络流量矩阵中OD流对的数量；A为路由矩阵，若第i条网络OD流经过第j条链路，则Ai，j=1，否则Ai，j=0.链路流量与网络流量矩阵的关系为

在网络流量矩阵测量过程中，假设进行Q次测量，各节点收集的链路流量数据为Y=（Y1，Y2，…，YQ）；对应的网络流量矩阵为X=（X1，X2，…，XQ）.

网络流量矩阵估计是在已知网络链路流量Y和路由矩阵A的情况下，获得X的估计值.由于通常情况下M ＜N，因此式（1）为欠定方程组，在没有额外信息的情况下上述方程组没有唯一解.

1.2 稀疏表示

研究［10］发现网络流量矩阵X具有低维特性：网络流量矩阵分解后的特征流低维空间可以描述其主要特征，K个主要的特征流分量占据了网络流量矩阵的大部分能量，特征流分量对应的奇异值代表其能量值.通过SVD分解可以得到重建网络流量矩阵的一组正交基，即

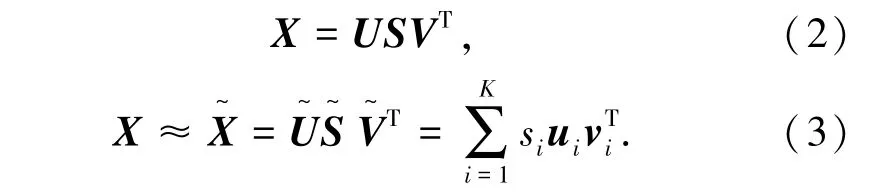
其中：si为X的奇异值；ui、vi分别为U和V的列向量.

将式（3）代入式（1），可得

其中：G为满足渐进正态分布N（0，O（M-1））的高斯随机矩阵；C（γ）为元素为0或1的对角阵，其对角线上0元素数量为γ；，在观测矩阵Ψ满足RIP原则的条件下，若已知正交基，则可以通过压缩感知理论完成重构Θ.

1.3 网络流量矩阵重构

在压缩感知框架下，对于式（5）可通过l0范数优化问题找到具有稀疏结构的解，即

其中：wq、θq分别为W和Θ的第q列（q=1，2，…，Q）矩阵.由于式（6）的优化问题是一个难求解的NP难问题，所以可以用l1约束取代l0约束，即

文献［12］通过正交匹配追踪算法对式（7）进行求解，具体步骤：1）设定算法输入观测信号wq，稀疏度K.2）初始化各参数.残差r0=wq，信号支撑集Φ0=∅.3）迭代计算.在第k（k=1，2，…，K）次循环，进行如下计算：a）从观测矩阵Ψ中寻找与信号相关性最强的信号支撑索引 I=arg将寻找到的信号支撑加入信号支撑集Φk=Φk-1∪ΦI；c）更新已选各列的稀疏系数估计值d）更新残差重构测量时间点q上的网络流量矩阵

2 稀疏度自适应的网络流量矩阵估计方法

在网络流量矩阵估计过程中，首先需要根据预先采集的部分网络流量矩阵信息进行SVD分解，寻找能够建立网络流量矩阵稀疏表示的稀疏基V～；随后在每个测量时间点单独应用正交匹配追踪算法计算该时间点上的网络流量矩阵数据.由式（3）可知，网络流量矩阵SVD分解后建立的稀疏表示本身存在截断误差，误差大小与稀疏度K的取值密切相关.当K值选择过小时，通过CS-OMP算法寻找的信号支撑集不够完备，难以完整描述网络流量矩阵的主要特征.当K值选择过大时，由于截断误差的存在使得CS-OMP算法有可能选取错误的索引位置并添加到信号支撑集.

文献［14］通过对大量实际网络的流量数据分析发现，能够描述网络流量矩阵的主成分数量一般在5～10个左右，且占据流量矩阵最高能量的成分所在的位置通常是固定不变的.根据上述结论，本文提出一种稀疏度自适应策略，首先根据对预先采集部分网络流量矩阵的PCA分析，计算各主成分的所占的能量值，结合初始稀疏度计算正交匹配追踪算法选择信号支撑集的判定阈值；随后在网络流量矩阵重构过程中，在各测量时间点上以残差衰减情况作为算法稀疏度的计算依据进行信号支撑集的选择，使得算法的稀疏度对于网络流量矩阵当前值具有自适应性，减少采用统一初始稀疏度产生的网络流量矩阵重构误差，提高网络流量矩阵的估计精度.

在对网络流量矩阵进行PCA分析时，由于网络流量矩阵数据本身是多维度数据，为减小不同维度数据幅值不同对PCA分析造成的误差，需要对网络流量矩阵数据进行标准化处理，即

式中：μq为第q次测量时获得的各网络OD流的均值；σq为第q次测量时获得的各网络OD流的协方差.

由于占据流量矩阵能量最高的成分的位置通常不变，因此考虑按照该成分所占的能量值对各主成分能量进行归一化处理，即

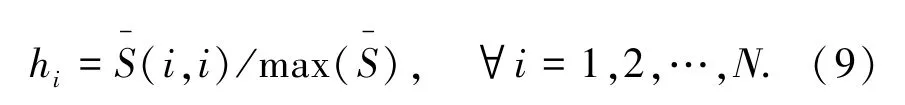
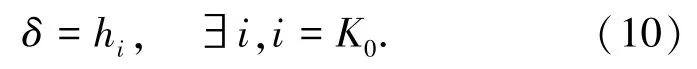
在2.3节所示网络流量矩阵重构过程中，重构误差主要来源于在每个测量时间点q上均要按照预先设置的初始稀疏度值进行K0次计算.但是由于受到稀疏表示本身误差及网络流量矩阵动态变化的影响，预先选择的K0不能准确地描述当前测量点上网络流量矩阵数据的稀疏度，容易导致选择错误的信号支撑集进行网络流量矩阵的重构.在正交匹配追踪算法进行信号重构过程中，信号支撑集中各分量所占的能量值大小可通过其当前残差的L2范数进行表征，而占据流量矩阵能量最高的成分所在的位置通常是不变的.因此本文采用归一化后的残差L2范数作为依据近似求解当前测量点上网络流量矩阵数据的稀疏度，在网络流量矩阵重构过程中按照下式寻找满足判定阈值的主成分中的最低能量所处的位置，即

在满足‖rK‖2／‖r0‖2≤δ后，认为已找到当前测量点上网络流量矩阵的稀疏度.如图1所示（图中横轴i为按能量值降序排列后的主成份序号，纵轴为归一化后的奇异值与残差l2范数的比值），初始稀疏度值取值为K0=10，经过PCA分析并对主成分能量进行归一化处理排序后，通过式（10）计算得到选择信号支撑集的判定阈值δ=0.21.在信号重构过程中，1. 3节步骤3经过5次迭代计算后的p5=0.21（见图中方框），因此当前时间点网络流量矩阵的稀疏度为5.

图1 自适应策略下的稀疏度计算过程

3 性能评估

本文采用Abilene骨干网的真实网络流量数据验证所提出算法 （adaptive orthogonal matching pursuit，AOMP）的各项指标.Abilene骨干网由12个节点路由器，30条内部链路和24条外部链路组成，主要用于教育与研究工作，其数据已广泛应用于网络测量的各个领域［15］.在本文中，可开展流量测量的链路数量M=54，待测量的网络OD流对数量为N=12×12=144，网络流量数据由NetFlow软件采集，采样间隔为5 min，连续采集1周时间得到的样本数为Q=2 016.为评价AOMP算法的性能，将与目前效果较好的CS-OMP算法［12］进行比较.

本文采用文献［10］给出的实验条件，选择采集1 d时间得到的OD流样本作为先验信息，样本数量为288.根据文献［14］的研究结论，能够描述网络流量矩阵的主成分数量一般在5～10个左右.为在相同条件下综合比较两种算法的性能，本文首先在文献［12］的初始稀疏度值（K0=10）下比较网络流量矩阵重构的精度，然后比较算法对初始稀疏度值（K0∈［5，6，7，8，9，10］）的自适应能力.

3.1 性能评价指标

空间相对误差eSRE：指某个OD流在各时间点上的测量值与真实值的相对误差，即

时间相对误差eTRE：指某个时间点上各OD流的测量值与真实值的相对误差，即

绝对误差均值eAE：指某个OD流在各时间点上的测量值与真实值偏差的均值，即

绝对误差标准差eSD：指某个OD流在各时间点上绝对误差的分布情况，即

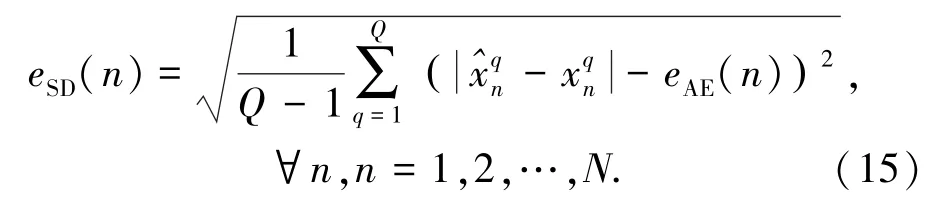
空间相对误差均值eASRE：指各OD流的空间相对误差的均值，即

时间相对误差均值eATRE：指各时间点上的时间相对误差的均值，即

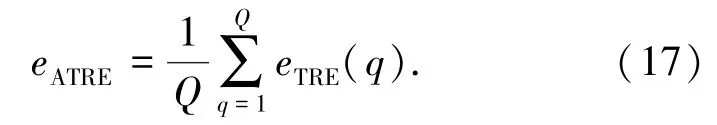
3.2 实验结果及分析

首先，考察两种算法对网络OD流的追踪能力.限于篇幅原因，本文仅通过图2、3列出其中两条OD流（编号为72和116）的估计值与真实值随时间点序号的变化情况，以展示两种算法对不同的OD流追踪性能.从图中可以看出，从整体上看两种算法都能跟踪网络OD流的变化趋势，但CS-OMP算法在每个时间点上都会引入相对较大的测量误差，其主要原因在于由于CS-OMP算法稀疏度是固定不变的，随着时间点的变化，预先设定的初始稀疏度逐渐不能很好地描述当前时间点上的网络OD流的稀疏情况，导致网络OD流重构时的误差增大.与之相比，AOMP算法在每个时间点上估计当前网络OD流的稀疏度，因此可以有效减小重构误差.

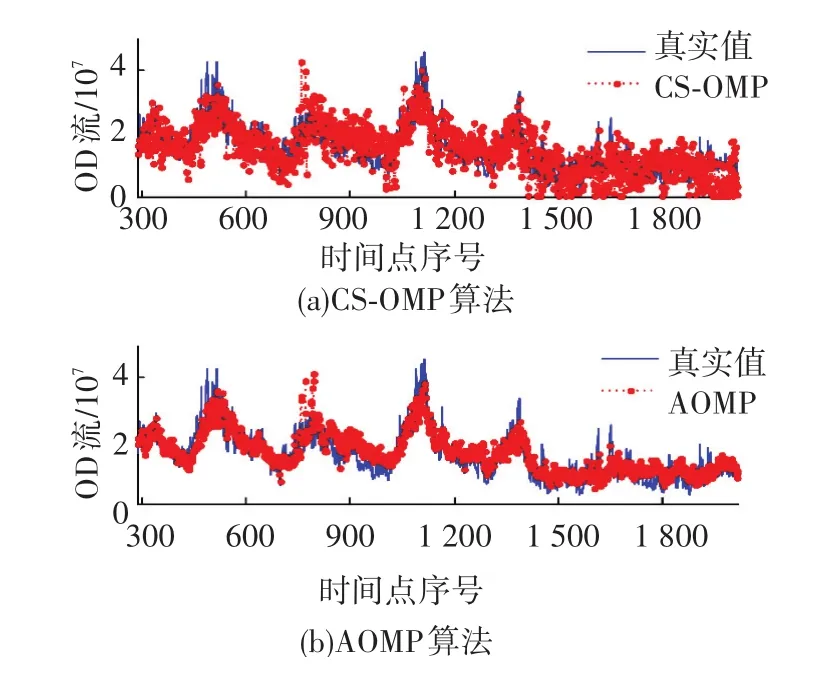
图2 第72条OD流真实值与估计值

图3 第116条OD流真实值与估计值

然后，比较两种算法对整个网络流量矩阵的估计能力.图4描述了空间相对误差随网络OD流编号（按照OD流均值升序排列）的变化情况和时间相对误差随时间点序号的变化情况.从图4可以看出，AOMP算法估计的网络流量矩阵空间相对误差与时间相对误差明显小于CS-OMP算法.

图4 空间相对误差与时间相对误差变化情况

图5描述了空间相对误差与时间相对误差的累积分布函数.从图5（a）可见，当空间相对误差为0.5时，AOMP算法估计出的网络流量矩阵的空间相对误差累积分布函数值为0.72；对于CS-OMP算法，对应的空间相对误差累积分布函数值为0.47.从图5（b）可见，在AOMP算法下，90%的网络流量矩阵中OD流的时间相对误差小于0.18；对于CS-OMP算法，达到该比例时的时间相对误差为0.27.

图5 空间相对误差与时间相对误差的累积分布函数

图6给出了上述两种算法的网络流量矩阵绝对误差均值随OD流编号（按照OD流均值降序排列）的变化情况.由图中可见AOMP算法估计出的网络流量矩阵绝对误差均值小于CS-OMP算法的估计结果，因此AOMP算法具有更高的网络流量矩阵测量正确度.

图6 各OD流的绝对误差均值分布情况

为比较两种算法对网络OD流估计的稳定性，本文采用网络流量矩阵绝对误差的标准差对其进行比较.图7描述了AOMP算法和CS-OMP算法估计出的网络流量矩阵绝对误差的标准差随绝对误差均值的变化情况，由图中可见AOMP算法绝对误差的标准差比CS-OMP算法更小，即AOMP算法估计出的结果具有更高的精密度.最后，验证AOMP算法对初始稀疏度的自适应性。图8和图9分别描述了网络流量矩阵空间相对误差均值和时间相对误差均值随初始稀疏度K0的变化情况，从图中可见AOMP算法的网络流量矩阵空间相对误差均值和时间相对误差均值都小于CS-OMP算法。随着初始稀疏度增大，CS-OMP算法的空间相对误差均值和时间相对误差均值逐渐增大，而AOMP算法则对初始稀疏度有良好的自适应性。

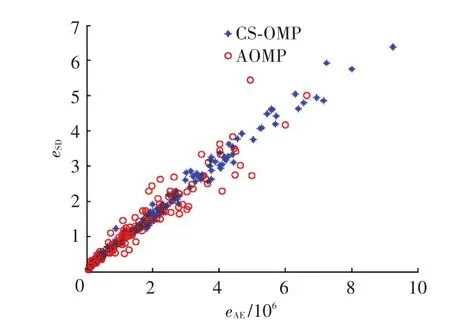
图7 绝对误差的标准差随绝对误差均值变化情况

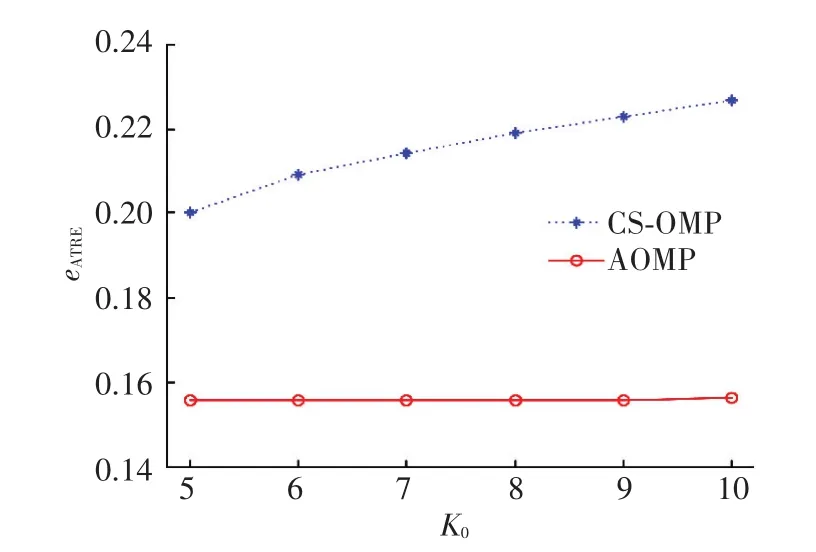
图9 时间相对误差随初始稀疏度变化情况

4 结 论

1）以网络层析成像技术为应用背景，在压缩感知框架下提出一种稀疏度自适应的网络流量矩阵测量方法.通过对基于压缩感知的网络流量矩阵测量方法重构算法分析，得出信号支撑集不够完备导致难以完整描述网络流量矩阵的主要特征是造成现有算法测量误差较大的主要原因的结论.

2）通过主成分分析方法计算网络流量各主成分所占的能量值，结合初始稀疏度计算正交匹配追踪算法选择信号支撑集的判定阈值.

3）在网络流量矩阵重构过程中，以残差衰减情况作为算法稀疏度的计算依据进行信号支撑集的选择，使得算法的稀疏度对于网络流量矩阵当前值具有自适应性.

4）对比CS-OMP算法，当初始稀疏度取值为10时，AOMP算法的时间相对误差降低50%左右；当初始稀疏度在5～10之间变化时，AOMP算法的空间相对误差均值和时间相对误差均值基本保持不变，表明其对于初始稀疏度选择具有良好的自适应性.

［1］周爱平，程光，郭晓军.高速网络流量测量方法［J］.软件学报，2014，25（1）：135-153.

［2］TOLEDO T，KOLECHKINA T.Estimation of dynamic origin-destination matrices using linear assignment matrix approximations［J］.IEEE Transactions on Intelligent Transportation Systems，2013，14（2）：618-626.

［3］杨京礼，孙超，姜守达，等.基于层次分解的网络链路时延分布快速推测算法［J］.电子与信息学报，2013，35（8）：2005-2012.

［4］ERIKSSON B，DASARATHY G，BARFORD P，et al. Efficient network tomography for internet topology discovery［J］.IEEE／ACM Transactions on Networking，2012，20（3）：931-943.

［5］ZHANG Y，ROUGHAN M，DUFFIELD N，et al.Fast accurate computation of large-scale IP traffic matrices from link loads［J］.ACM SIGMETRICS Performance Evaluation Review，2003，31（1）：206-217.

［6］ VARDIY.Network tomography： estimatingsourcedestination traffic intensities from link data［J］.Journal of American Statistical Association，1996，91（4）：365-377.

［7］ LIANG Gang， YU Bin.Maximum pseudo likelihood estimation in network tomography［J］.IEEE Transactions on Signal Processing，2003，51（8）：2043-2053.

［8］VATON S，BEDO J.Network traffic matrix：how can one learn the prior distributions from the link counts only？［C］／／Proceeding of IEEE Conference on Communications 2006.Paris：IEEE，2006：2138-2142.

［9］EUM S，MURPHY J，HARRIS R.A fast accurate LP approach for traffic matrix estimation［C］／／Proceeding of ITC19.Beijing：IEEE，2005：243-252.

［10］SOULE A，LAKHINA A，TAFT N，et al.Traffic matrices：balancing measurements，inference and modeling［C］／／Proceeding of SIGMETRICS Conference on Measurement and Modeling of Computer Systems 2005.Banff：ACM，2005：362-373.

［11］QIAN Feng，HU Guangmin，XIE Jijun.A recurrent neural network approach to traffic matrix tracking using partial measurements ［C］／／Proceeding of the 3rd IEEE Conference on Industrial Electronics and Applications. Singapore：IEEE，2008：1640-1643.

［12］NIE Laisen，JIANG Dingde.A compressive sensing-based network tomography approach to estimating origindestination flow traffic in large-scale backbone networks［J］.International Journal of Communication Systems，2014，27（4）：1-12.

［13］NIE Laisen， JIANG Dingde， XU Zhengzheng.A compressive sensing-based reconstruction approach to network traffic［J］.Computers and Electrical Engineering，2013，39（5）：1422-1432.

［14］LAKHINA A，PAGIANNAKI K，CROVELLA M，et al. Structuralanalysis ofnetwork traffic flows ［C］／／Proceeding of SIGMETRICS Conference on Measurement and Modeling of Computer Systems 2004.New York：ACM，2004：61-72.

［15］YIN Z，MATTHEW R，WALTER W，et al.Spatiotemporal compressive sensing and internet traffic matrices［J］.IEEE／ACM Transactions on Networking，2012，20（3）：662-676.

（编辑 魏希柱）

A sparsity adaptive measurement algorithm for network traffic matrix

YANG Jingli，CUI Zheng，WEI Chang’an，JIANG Shouda

（Department of Automatic Test and Control，Harbin Institute of Technology，150080 Harbin，China）

In order to improve the accuracy of the measurement algorithm for traffic matrix，a novel traffic matrix measurement algorithm with compressive sensing is proposed.This algorithm gets the judge gate by the principal components analysis and normalization of singular value.To reduce the measurement error created by approximation of sparse express and inaccurate choice of sparsity，we use L2 formulation of residual error to match the sparsity in the process of reconstitution of the traffic matrix on each time of measurement.Simulation results show that，this algorithm can obtain less spatial relative error and temporal relative error compared with the existing algorithm.With the help of adaptive selection for initial value of sparsity，this algorithm can obtain a higher accuracy.

network measurement；network tomography；traffic matrix；compressive sensing；orthogonal matching pursuit

TP393

A

0367-6234（2015）09-0013-06

10.11918／j.issn.0367-6234.2015.09.003

2014-07-03.

国家自然科学基金（61501135）；黑龙江省博士后基金（LBH-Z11171）.

杨京礼（1984—），男，博士，助理研究员.

杨京礼，jinglidg＠hit.edu.cn.