基于动网格井巷活塞风影响因素的数值模拟研究

邬长福，邓权龙，李乐农

(1.江西理工大学江西省矿业工程重点实验室，江西 赣州 341000；2.江西通安安全评价有限公司，江西 赣州 341000)

基于动网格井巷活塞风影响因素的数值模拟研究

邬长福1，邓权龙1，李乐农2

(1.江西理工大学江西省矿业工程重点实验室，江西 赣州 341000；2.江西通安安全评价有限公司，江西 赣州 341000)

为了研究不同因素对井巷活塞风的影响，运用控制变量法，选取了矿车速度Vc、巷道风速V0、阻塞比а三种影响因素，采用基于动网格技术的标准k-ε双方程湍流模型对巷内气流组织进行数值模拟，得到了不同因素对巷内气流组织影响的变化规律。研究结果表明：随着车速的提高，巷内活塞风效应和影响效力和范围增大；当风流与矿车同向时，随着风速增大活塞风效应越不明显，对矿井通风影响越小；当风流与矿车反向时，随着风速增加车头与车尾压差、风流紊乱程度、通风阻力均变大，对通风效果影响较大；活塞风效应随着阻塞比的提高越来越明显，对巷内通风干扰变大。

安全工程；矿井通风；活塞风；数值模拟；动网格

运输设备在运输过程中，巷道内风流受限于巷道壁面产生活塞风效应，致使风流流场发生变化，影响预期通风效果。随着工业的迅速发展，矿产需求大量化，矿山最直接有效的办法便是提高运输设备的速度，却使井巷活塞风效应更明显。传统矿井通风方面的研究并未对活塞风效应做深入探究，因此研究活塞风效应的影响因素具有重要意义，为减弱井巷活塞风效应提供理论指导。

关于活塞风的研究最早源于车辆通过隧道引起的空气动力学问题，在公路、铁路隧道、地铁空调等工程中研究得较多，而在矿井通风领域研究较少。国内，学者王海桥、田锋等对矿井井筒提升设备绕流进行了理论分析和数值模拟[1]；吴超、王从陆等应用Fluent软件对矿井巷道运输工具的活塞风进行了模拟分析[2]。本文选用尺寸近似于实际井巷矿车运输的二维模型，用Gambit前处理器建立模型并划分网格，然后导入Fluent 6.3.26软件中设定计算参数，主要对巷内风流组织速度场和压力场进行模拟[3-5]。本文选择了矿车速度Vc、巷道风速V0和阻塞比а这三种影响因素，运用控制变量法确定三组方案，分别模拟单一因素对井巷活塞风的影响。

1 井巷活塞风效应的计算模型

1.1 数学模型

由于矿车在井巷中运行使流场发生复杂变化，为合理简化计算模型，现做如下假设：①巷内风流流动为不可压流动；②假定巷内壁面绝热、风流等温流动；③流体的紊流粘性具有同向性，紊流粘性系数可作为标量处理，且满足Boussinesq假设。紊流模型采用标准k-ε双方程模型[6-10]。连续方程见式(1)，动量方程见式(2)，k方程见式(3)，ε方程见式(4)。

(1)

(2)

(3)

(4)

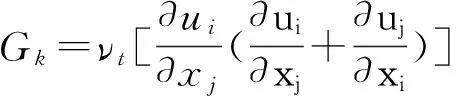
1.2 几何模型

根据矿山井巷和矿车的实际尺寸，结合本论文的主要研究对象为井巷设备运输活塞风效应的影响因素，研究对象简化为一段长度为50m的运输巷道，其断面为矩形，宽3.0m，高2.4m；矿车尺寸为长6.0m，高1.6m，宽度根据各方案而定，其中方案一、方案二均取1.6m，方案三则分别取1.2m、1.6m、2.0m。如图1所示，将矿车和运输巷道分别简化为矩形，建立二维几何模型。

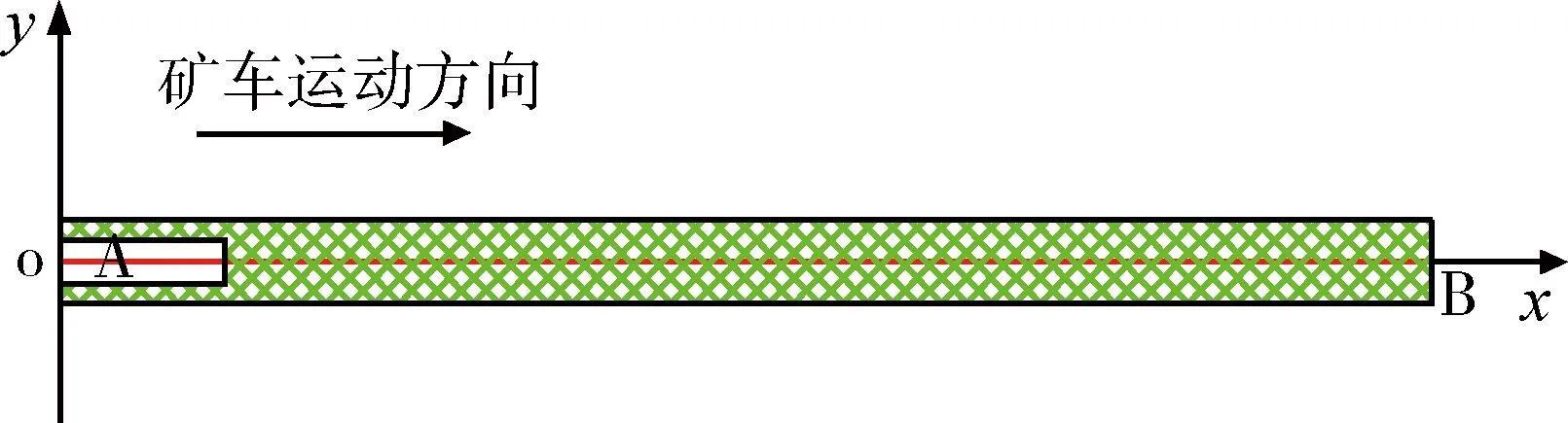
图1 井巷矿车运输几何模型

2 条件设置和动网格技术

2.1 网格划分

利用前置模型处理软件Gambit，根据各方案需要，建立相应尺寸的二维几何模型，经过布尔Subtract运算后，对模型进行网格划分。对巷道两长边进行0.2 m等间距划分，其余边进行0.1 m等间距划分，最后对总体面网格进行非结构化三角形划分。

2.2 边界条件

如上图1所示，设巷道左侧边界为巷道入口，根据不同方案选择压力进口(pressure-inlet)或速度进口(velocity-inlet)；巷道右侧边界为巷道出口，设为压力出口(pressure-outlet)。矿车的四边设为固壁边界(wall)，其余边界默认。

2.3 动网格设定

矿车在井巷中运行属于移动与变形区域流动问题，本文模拟选用动网格模型(Dynamic Mesh)，先指定区域中的刚性体和流体区域，再将Profile文件导入Fluent 6.3.26软件对矿车运动方向和速度进行控制，通过选定弹性光顺法(spring-base smoothing)和局部网格重划法(local remeshing),前者设定弹簧因子(spring constant factor)为0.3，后者设定最小合并尺寸(Minimum Length Scale)为0.1 m，最大分裂尺寸(Maximum Length Scale)为0.3 m，其他参数保持默认[6]。

2.4 求解方法

采用基于压力隐式分离的解算器，选择二维非恒定流动(一阶隐式)，速度为绝对速度，湍流模型选用标准k-ε双方程模型，流场求解计算方法选择Simple算法。

3 模拟方案及结果分析

拟分析矿车速度Vc、巷内风速V0、阻塞比а对活塞风效应的影响，采用控制变量法，模拟这三种因素分别对井巷活塞风速度和压力分布的影响。此外，为了便于分析，取巷道中心线AB作为监测对象，如图1所示，其中A坐标(0，0)、B坐标(50,0)，取巷道长度为横坐标，取不同因素下的速度、压力分别为纵坐标，便得到不同影响因素巷道中心线AB速度和压力分布曲线。

3.1 方案一：矿车速度Vc对井巷活塞风的影响

本方案是保持矿车巷内风速V0、阻塞比a不变，通过改变矿车速度Vc,模拟巷内风流速度场和压力场。设定巷道风流速度V0为0m/s，阻塞比a等于矿车断面面积(1.6m×1.6m)与巷道断面面积(3.0m×2.4m)之比为0.36，矿车从横坐标x=0处开始运行，选取车速Vc分别为3m/s、6m/s、9m/s 三种情况，模拟巷道活塞风速度场(如图2)和压力场云图(图4)。在巷道中心线AB监测不同车速情况运行相同路程时的速度和压力的大小，便得到不同车速时巷道中心线AB速度分布曲线(图3)和压力分布曲线(图5)。

图2 不同车速时活塞风速度场云图

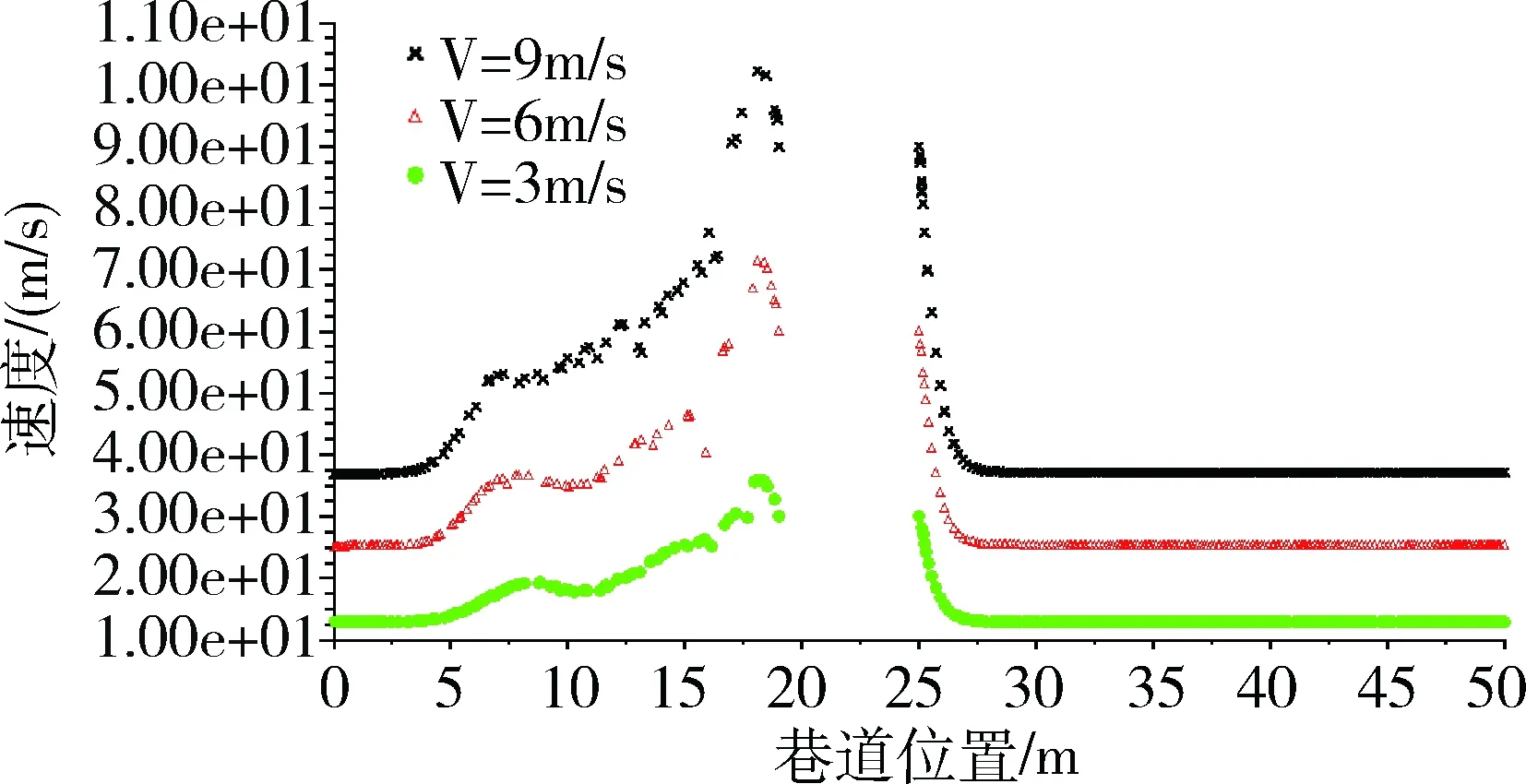
图3 不同车速时巷道中心线AB速度分布曲线

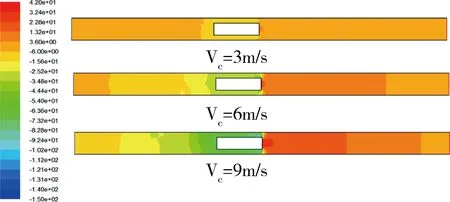
图4 不同车速时活塞风压力场云图

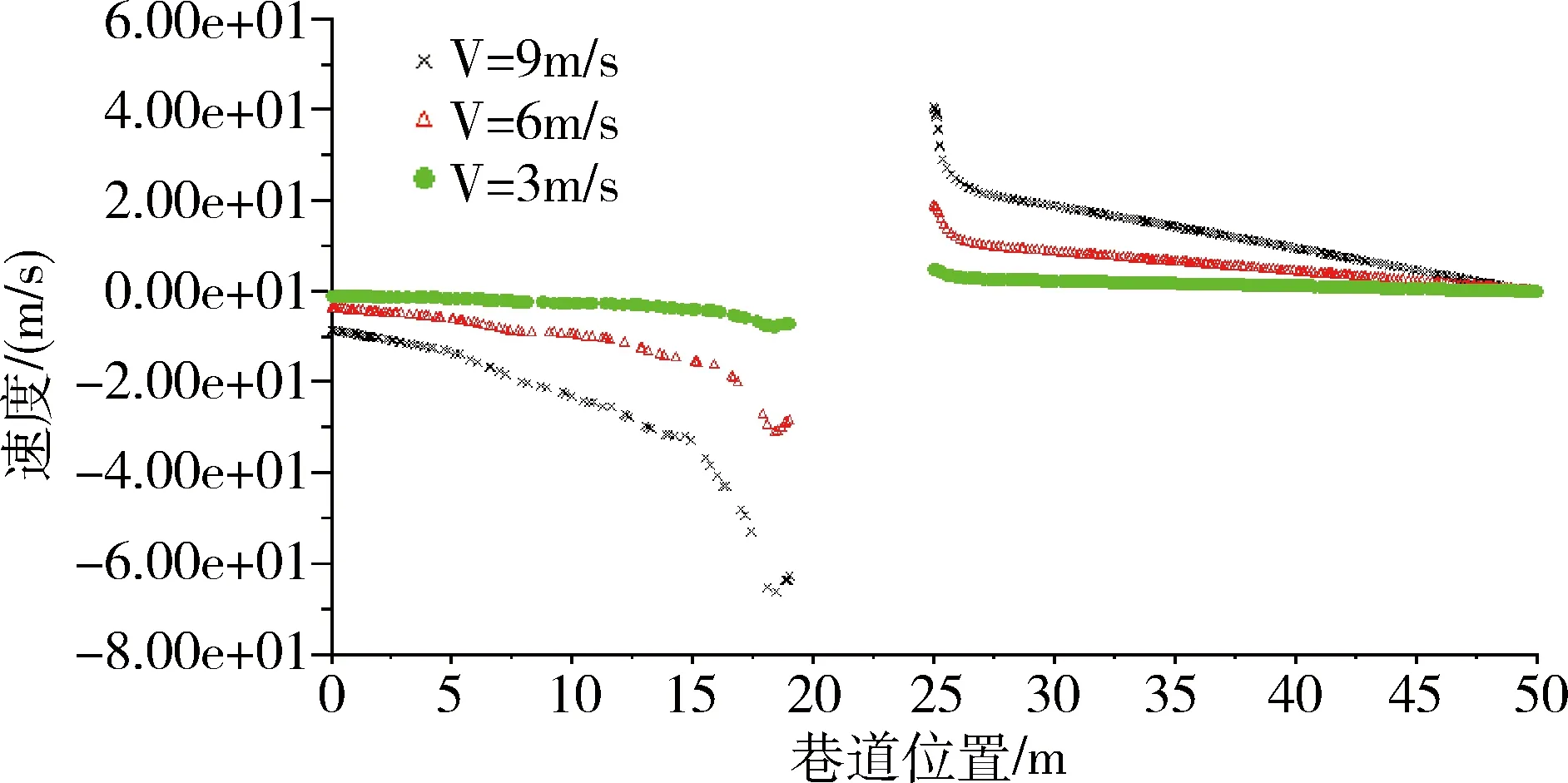
图5 不同车速时巷道中心线AB压力分布曲线

如图2所示，为矿车车速在3m/s、6m/s、9m/s三种情况下巷内风流速度流场的云图，通过三者比较而知，车速为3m/s时，巷内活塞风效应不明显，影响范围较小；当车速达到6m/s时，巷内风流场有较大的变化，活塞风效应较明显，影响的流域范围增大；当车速升至9m/s时，活塞风效应非常明显，巷内流场区域的流速明显增大。

如图3所示，为不同车速时巷道中心线AB上速度分布曲线，当车速为3m/s时，车头处风流最大速度约3m/s，车尾部最大流速约为3.75m/s，两者之差为0.75m/s，巷内产生活塞风风速约为1.25m/s。当车速为6m/s时，车头处风流最大速度约6m/s，车尾部最大流速约为7.25m/s，两者之差为1.25m/s，巷内产生活塞风风速约为2.50m/s。当车速为9m/s时，车头处风流最大速度约9m/s，车尾部最大流速约为10.25m/s，两者之差为1.25m/s，巷内产生活塞风风速约为3.60m/s。

如图4所示，通过三者比较可知，车速为3m/s时，巷内压力变化不明显，车头与车尾压差较小；当车速达到6m/s时，巷内压力有较大的变化，车头前部区域的压力(正值)有所升高，车头后部的压力(负值)明显降低，车头与车尾压差增大；当车速为9m/s时，巷内流场区域的压力变化较为显著，且车头与车尾压差明显变大。

如图5所示，当车速为3m/s时，车头部压力约7.5Pa，车尾部压力约为-7.5Pa，两者之差为15.0Pa。当车速为6m/s时，车头部压力约19.8Pa，车尾部压力约为-29.5Pa，两者之差为49.3Pa。当车速为9m/s时，车头部压力约42.0Pa，车尾部压力约为-62.5Pa，两者之差为104.5Pa。

经过对不同车速下活塞风效应影响模拟结果进行比较分析，可得出：随着车速的提高，巷内活塞风效应越来越明显，影响效力和范围增大，巷内流场流速和压力变化变大，产生的活塞风风速逐渐升高，车头部与车尾部压差变大。

3.2 方案二：巷内风速V0对井巷活塞风的影响

本模拟方案是保持矿车车速Vc、阻塞比a不变，通过改变巷内风速V0，得到巷内风流速度场和压力场。设定矿车速度Vc为5m/s，运行4s即运行路程为20m，阻塞比a等于矿车断面面积(1.6m×1.6m)与巷道断面面积(3.0m×2.4m)之比为0.36，矿车从横坐标x=0处开始向x正方向运行，选取风速V0分别为+4m/s、+2m/s、0m/s、-2m/s、-4m/s五种情况，模拟巷道活塞风速度云图(图6)和压力云图(图7)。在巷道中心线AB监测4s时刻不同风速的速度和压力的大小，便得到不同风速时巷道中心线AB速度分布曲线(图8)和压力分布曲线(图9)。

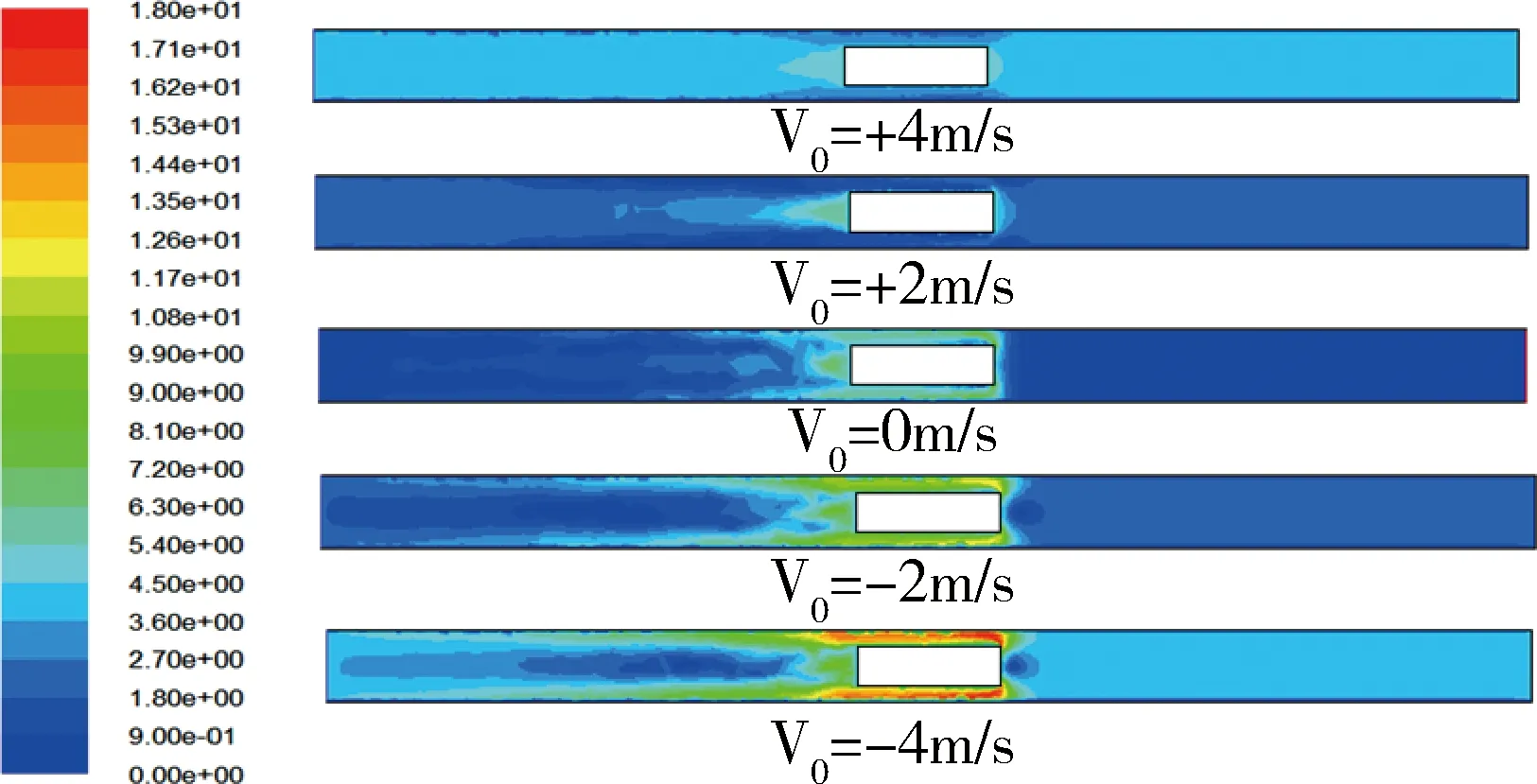
图6 不同风速时活塞风速度场云图

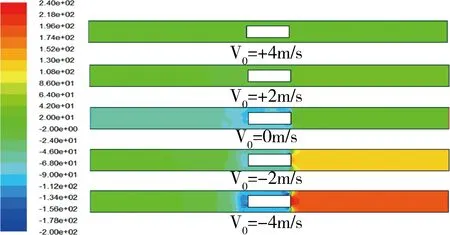
图7 不同风速时活塞风压力场云图

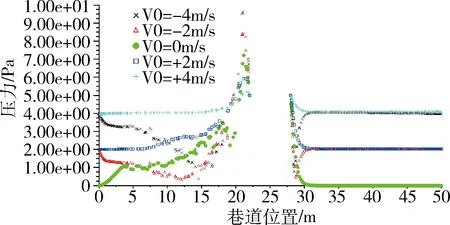
图8 不同风速时巷道中心线AB速度分布曲线

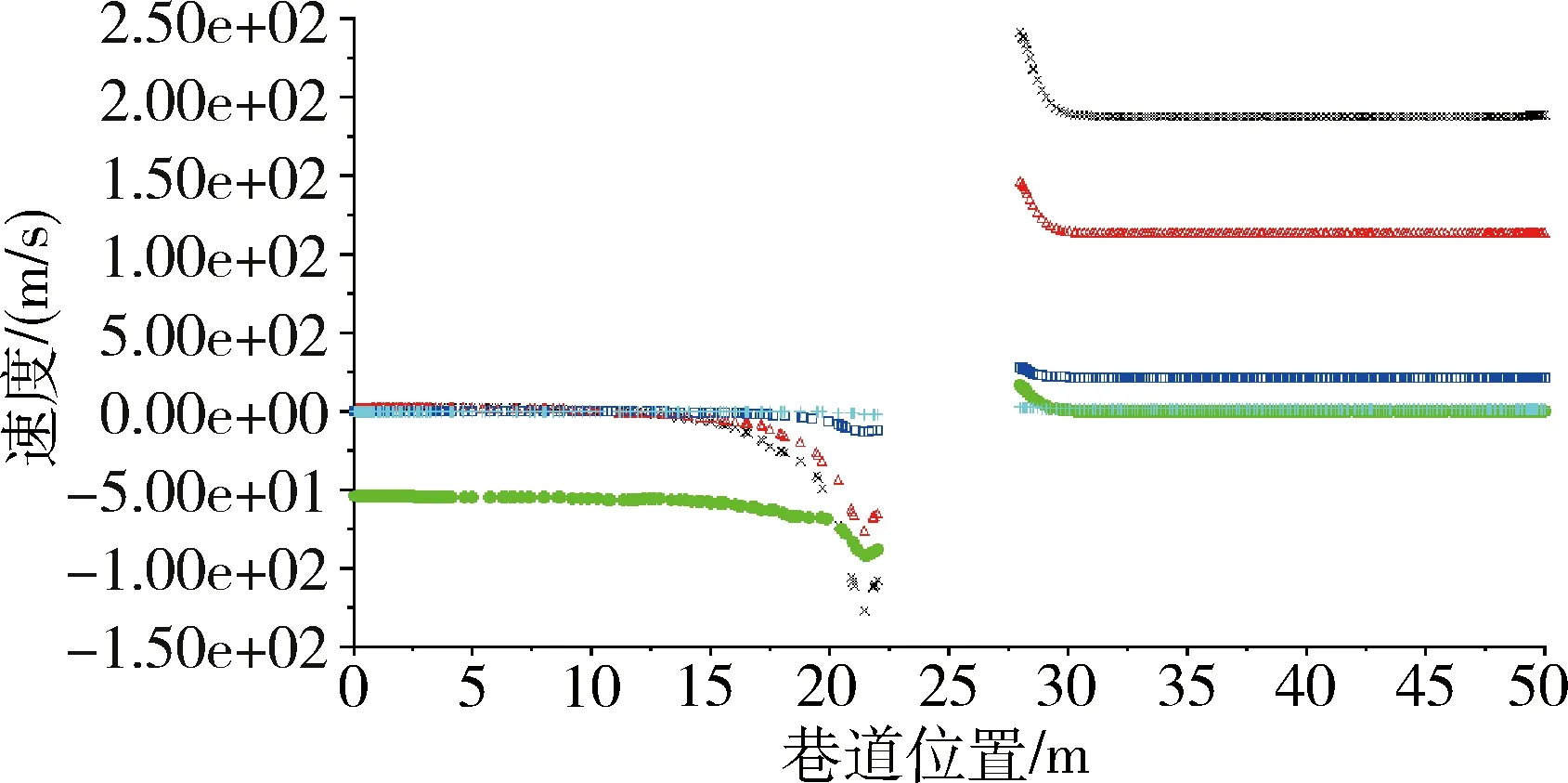
图9 不同风速时巷道中心线AB压力分布曲线

如图6、图7所示，共设置了风速为+4m/s、+2m/s、0m/s、-2m/s、-4m/s 五组模拟试验，包括风流方向与车速方向相同、方向相反和风速大小为0三种情况，其中风速大小为0的情况作为参照。通过比较风速为+4m/s、+2m/s、0m/s三种情况(风速方向与车速方向相同时)的模拟结果，可以看出：当风速为+4m/s时，车尾处速度峰值约为5.25m/s，巷内活塞风效应现象不明显；当风速为+2m/s时，车尾处速度峰值约为6.15m/s，巷内活塞风效应现象较为明显；当风速为0m/s时，车尾处速度峰值约为7.25m/s,巷内活塞风效应现象非常明显。当风速与车速方向相反时，即风速为-2m/s、-4m/s时，巷道内原来的风速方向与活塞风风速方向相反，在车头前部的风流速度场比较稳定；但是在车身与巷道之间的环隙空间的流速经过叠加，速度大小急剧变大；车尾后部流场速度场出现紊乱，靠近巷道壁面的速度较大，巷道中心线附近的风速较小。

如图7、图9所示，当风速与车速方向相同时，巷道内的压力场变化不大，当风速为+4m/s时，车头与车尾的压差约为6Pa；当风速为+2m/s时，车头与车尾的压差约为22Pa。当风速为0时，车头部的压力约为15Pa，车尾部的压力约为-95Pa，两者压差为110Pa。当风速与车速方向相反时，巷内流域的压力变化较大，当风速为-2m/s时，车头部的压力约为150Pa，车尾部的压力约为-75Pa，两者压差为225Pa；当风速为-4m/s时，车头部的压力约为246Pa，车尾部的压力约为-125Pa，两者压差为371Pa。

综合分析方案二的模拟结果可得出：当风流与车速方向相同时，随着风速增大，活塞风风速越小，活塞风效应越不明显，对矿井通风影响越小。当风速与车速方向相反时，随着风速增加，车头与车尾压差增大，通风紊乱程度大，对通风效果影响较大。

3.3 方案三：阻塞比a对井巷活塞风的影响

本方案是保持矿车车速Vc、巷内风速V0不变，通过改变阻塞比a模拟得到巷内风流速度场和压力场。设定矿车速度Vc为5m/s，运行4 s即运行路程为20 m，巷内风速V0为0m/s，阻塞比a即为矿车断面面积/巷道断面面积，通过使用不同型号的矿车，其断面不同，分别选取B×H为1.2m×1.6m、1.6m×1.6m、2m×1.6m，保持巷道断面B×H=3m×2.4m不变，从而得到阻塞比a分别为0.27、0.36、0.44，模拟巷道活塞风速度场云图(图10)和压力场云图(图11)。在巷道中心线AB监测运行4s时刻不同阻塞比a情况下的速度和压力的大小，便得到不同阻塞比时巷道中心线AB速度分布曲线(图12)和压力分布曲线(图13)。

如图10、图12所示，当阻塞比a为0.27时，巷内活塞风速度流场云图较为明显，巷道中心线AB上监测的活塞风风速达到了1.45m/s；当阻塞比a为0.36时，巷内活塞风速度流场云图非常明显，巷道中心线AB上监测的活塞风风速达到了2.20m/s；当阻塞比a为0.44时，巷内活塞风速度流场云图最为明显，巷道中心线AB上监测的活塞风风速达到了3.15m/s。

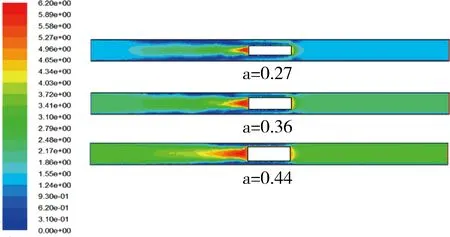
图10 不同阻塞比时活塞风速度云图

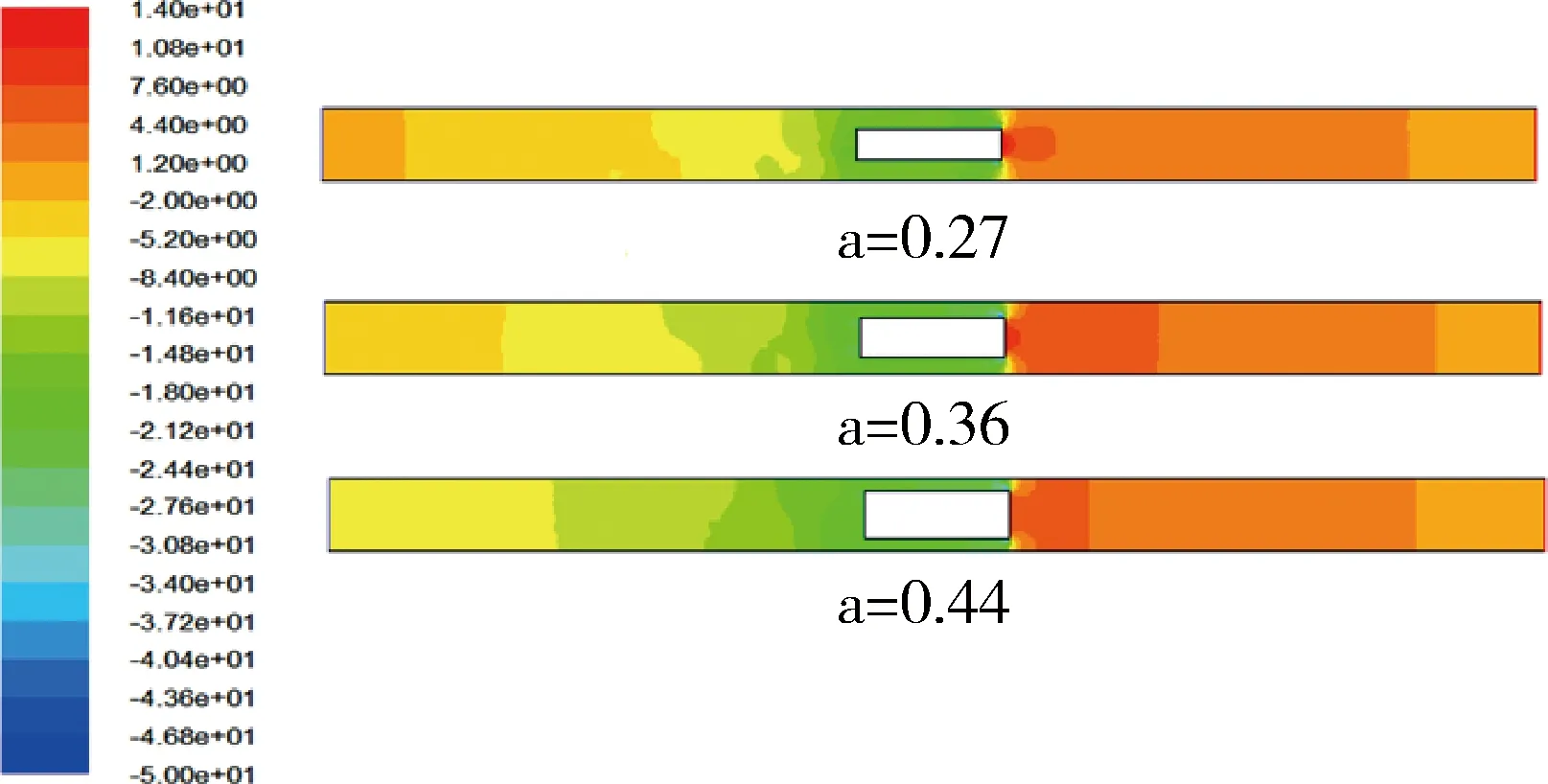
图11 不同阻塞比时活塞风压力云图

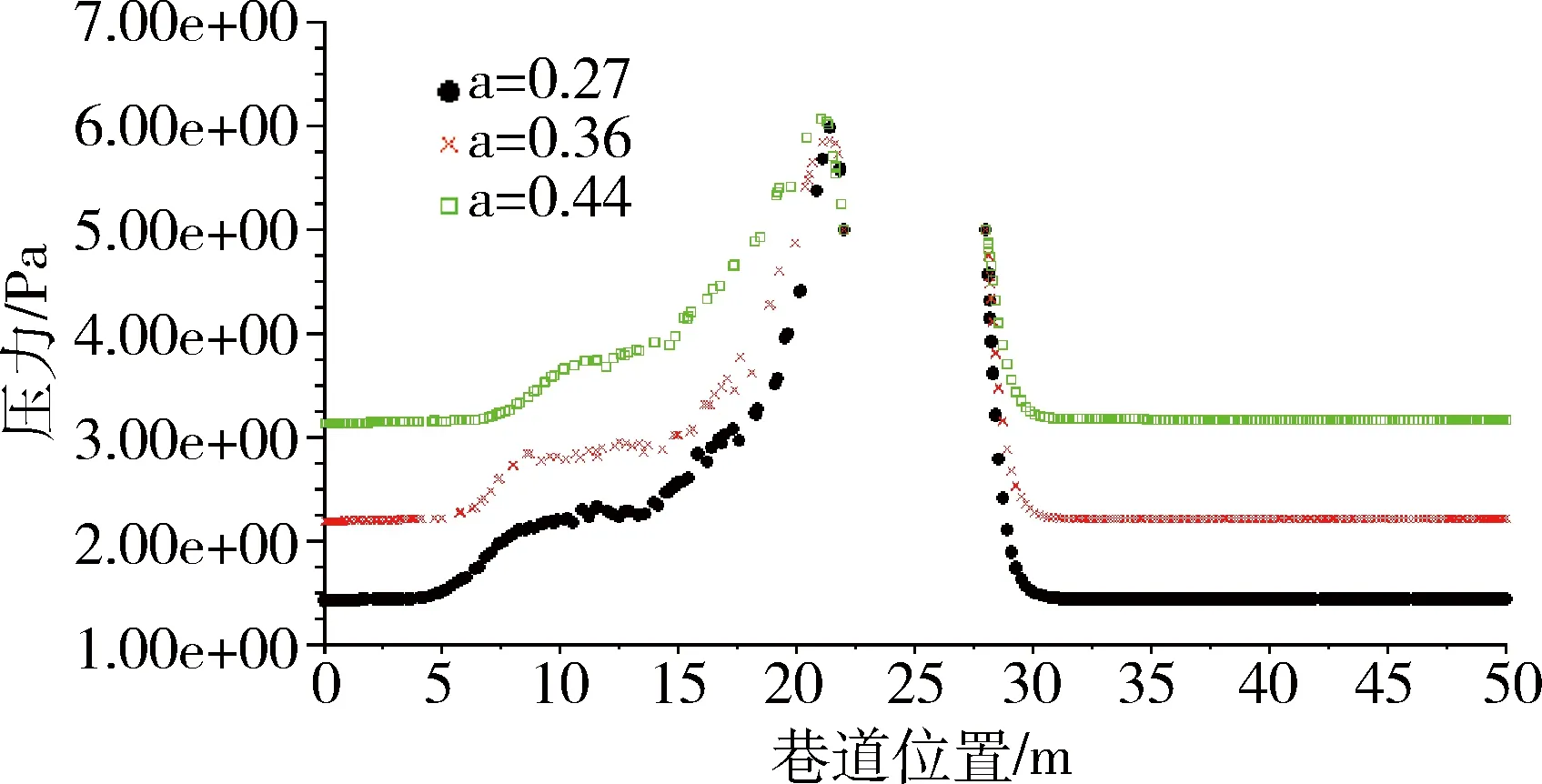
图12 不同阻塞比时巷道中心线AB速度分布曲线

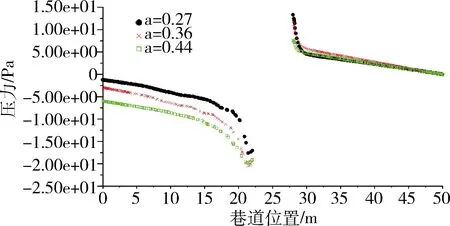
图13 不同阻塞比时巷道中心线`压力分布曲线

如图11所示，三组不同阻塞比a情况下，巷内流场压力云图均比较明显，但是相比较而言，a=0.44时最为明显，a=0.36时次之，a=0.27时最不明显。如图13所示，为巷道中心线AB上监测的活塞风压力大小，三种阻塞比情况下车头前部的压力(为正值)大小分布曲线基本重合，区别不明显；车尾后部的压力(为负值)大小分布情况：a=0.44时压力值最大，a=0.36时次之，a=0.27时压力值最小。

通过对本方案的模拟结果进行分析而知：随着阻塞比的增大，活塞风效应现象越明显，活塞风风速随之增大，巷内压差增大。

4 结论

1)矿车速度的提高导致活塞风效应越来越明显：活塞风风速升高，车头与车尾压差变大，流场内流速和压力变化幅度变大，影响效力和范围增大。所以，适当地控制减小矿车速度，能够减弱活塞风对井巷通风的干扰。

2)当风流与矿车同向时，随着风速增大，活塞风风速越小，活塞风效应越不明显，对矿井通风影响越小。当风流与矿车反向时，随着风速增加，车头与车尾压差增大，通风紊乱程度大，通风阻力变大，对通风效果影响较大。

3)随着阻塞比的增大，活塞风效应现象越明显，活塞风风速随之增大，巷内压差增大，不利于井巷通风，应适当减小阻塞比。

[1] 王海桥，田峰，黄俊歆，等.矿井井筒提升设备绕流的数值模拟[J].中国安全科学学报，2006，16(9)：29-33.

[2] 王从陆，吴超，王卫军.活塞风数值模拟及在矿内运输巷道中的应用[J].安全与环境学报，2007，7(3)：120-123.

[3] 张师帅.计算流体动力学及其应用-CFD软件的原理与应用[M].武汉：华中科技大学出版社，2011.

[4] G.X.Wu and Z.Z Hu.Numerical simulation of viscous flow around unrestrained cylinders [J].Journal of Fluids and Structures，2006,(22)：371-390.

[5] Jack L B，Cheng C，Lu W H.Numerical simulation of pressure and airflow response of building drainage ventilation systems[J].Building Service Engineering，2006，27(2)：201-205.

[6] 周俊杰，徐国权，张华俊.FIUENT工程技术与实例分析[M].北京：中国水利水电出版社，2013.04.

[7] 王从陆，吴超.基于移动参考框架的矿内运输工具活塞风数值模拟[J].煤炭学报，2007，32(8)：838-841.

[8] 邬长福,吴惠萍,刘赟.风速对管道天然气泄漏扩散影响的数值模拟 [J].工业安全与环保，2013，39(12)：46-49.

[9] 王刚，孙晋安，王海洋.基于Fluent对火区下近距离煤层工作面CO异常涌入的数值模拟[J].中国矿业，2013，22(6)：101-105.

[10] 伍贻兆，田书玲，夏健.基于非结构动网格的非定常流数值模拟方法[J].航空学报，2011，32(1)：15-26.

Numerical simulation of laneway piston pind under different influence factors based on dynamic mesh

WU Chang-fu1，DENG Quan-long1，Li Le-nong2

(1.Jiangxi Key Laboratory of Mining Engineering，Jiangxi University of Science & Technology，Ganzhou 341000，China；2.Jiangxi Tongan Secutity Assessment Co..Ltd.，Ganzhou 341000，China)

This paper is aimed to study the influence of different factors on the laneway piston wind，under the influence factors of tramcar speed，laneway wind speed and blockage ratio，there are four simulation schemes with the application of control variable method，and the numerical simulation of airflow distribution of laneway byk-εturbulence model based on dynamic mesh is proposed.The numerical simulation results show thatk-εturbulence model and dynamic mesh method could properly simulate the airflow distribution and tramcar operation；the piston wind influence range become larger with the increase of tramcar speed；when airflow and tramcar move in the same direction，the piston wind effect is less evident and the influence on laneway ventilation is smaller with the increase of wind speed；when airflow and tramcar move in the opposite direction，the differential pressure between the tramcar front and rear is greater，airflow turbulence is more obvious，ventilation resistance and the influence on laneway ventilation grow larger with the increase of wind speed；the larger blockage ratio，the more obvious the piston wind effect，and the disturbance to laneway ventilation grows larger.

safety engineering；mine ventilation；piston wind；numerical simulation；dynamic mesh

2014-12-20

邬长福(1963-)，男，江西贵溪人，硕士，现任教授，硕士生导师，主要从事矿井通风优化设计研究、工业灾害事故预防方面的教学与研究工作。E-mail：beyond100001@163.com。

TD 727

A

1004-4051(2015)08-0110-05