面向目标导向的软件演化过程行为的研究

黄世反,沈勇,2,王道红,康洪炜,2,郑见琳,贾书伟

(1.云南大学 软件学院，云南 昆明 650091; 2.云南大学 云南省软件工程重点实验室，云南 昆明 650091;3.云南省农村信用社 科技结算中心，云南 昆明 650000)

面向目标导向的软件演化过程行为的研究

黄世反1,沈勇1,2,王道红3,康洪炜1,2,郑见琳1,贾书伟1

(1.云南大学 软件学院，云南 昆明 650091; 2.云南大学 云南省软件工程重点实验室，云南 昆明 650091;3.云南省农村信用社 科技结算中心，云南 昆明 650000)

对软件演化过程行为的分析有助于在演化前期阶段发现一些不合理的设计情况，从而达到降低软件演化的风险.在面向目标导向的软件演化过程模型的基础上，使用通信顺序进程的原理对软件演化过程的行为进行了研究，分别从过程的迹、确定性和不确定性等方面进行了深入的分析，并给出了每一种行为的计算方法.

通信顺序进程;目标导向;软件演化过程;过程行为

软件演化是指在软件的整个生命周期之内所进行的对软件进行维护和更新的行为和过程，最早对软件演化这一现象进行研究的是 Lehman 等人，他们从对 IBM 软件开发过程的研究中提出了软件演化的概念，继而总结出了软件演化的八大定律[1]；由软件开发团体、软件工程学院(SEI)及Carnegie Mellon大学共同开发的CMM(capability maturity model)把软件开发视为一个过程，并根据这一原则对软件开发和维护进行过程监控和研究，以使其更加科学化、标准化、使企业能够更好地实现商业目标[2].Osterweil等[3]提出了一个著名的观点：“软件过程也是软件”，认为软件过程和软件一样具有相同的特性.ISO/IEC 15504是一个新兴的软件过程评估的国际标准，它定义了大量的软件工程过程和测量其能力的尺度，Eman等[4]对ISO/IEC15504中软件需求分析(SRA)过程能力评估的预测效度进行了实证研究，发现对于规模较小的企业，预测有效性的证据是相当弱的.Lehman等[5]把软件演化过程模型看作是一个多层次多循环的反馈系统，同时还提出了一种E类型的软件演化动态建模的方法.文献[6]从平台、技术、模型等方面对软件的动态演化进行了全方位的探讨与研究，但涉及到过程方面的研究却很少；在软件演化过程方面的研究以李彤[7]最为著名，在《An Approach to Modelling Software Evolution Processes》一书中做了详细深入的研究，他提出了一个形式化的软件演化元模型(EPMM)，并把EPMM分为4个层次：任务层、活动层、过程层和全局层，同时还提出了演化过程的描述语言(EPDL)，对软件演化过程中效率的改进等做了全面、细致的研究，在软件演化过程的研究中独树一帜.

随着日益增多的遗产系统，软件演化过程变得日益重要[7]，为了加深对软件演化过程的了解以及很好的管理演化过程中的每一个活动，必须对软件演化过程进行建模，软件演化过程的模型是对软件演化工作中所有活动的一个抽象描述，通过对软件演化的过程建立模型，使得相关人员可以对软件演化中的各项活动和任务有清晰的认识和掌控.软件演化过程行为是在所建立的模型基础之上，对软件演化中活动发生的一种抽象描述，对软件演化过程行为进行研究能够提前对软件在演化过程中所发生的情况做出准确的判断.

在软件演化过程中，不同的角色、人员所关注的焦点并不相同，譬如项目经理只关心某个过程是否按进度进行，至于过程里具体的活动和任务的进度就不太关心；对于管理某个具体过程的负责人来说，其所关注的焦点主要集中在该过程的活动或任务之上，为满足这项要求，本文在对过程行为进行分析的同时，分别从过程层和活动层进行详细的阐述.本文主要研究工作包括：基于目标和环境提出了一种基于目标导向的软件演化建模的模型GDSEPM(goal directed software evolution process model)；基于GDSEPM，对软件演化过程建模的方法、步骤和应遵行的原则进行了详细讨论，并给出了基于目标导向的软件演化过程建模的算法；使用通信顺序进程的原理对软件演化过程的行为(过程的发散、绝境、浑沌)进行了深入的分析并给出了相应的求解过程.

1 目标导向的软件演化过程模型

定义1[8]目标状态是用于标识一个目标的行为状态.令目标状态的集合为GoalState，典型元素是τ，定义为τ::=INI|ACT|SUS|SUC|FAI.其中INI标识目标的初始状态，ACT标识目标处于活动状态，SUS标识目标处于等待状态，SUC标识已经执行成功，FAI标识目标已经失败.

定义2 目标是一个四元组:goal=(gid,GS,ST,τ)，其中：gid是目标的唯一标识号；GS是一组目标描述,GS= {gs1,gs2,…,gsn}；ST是一组评定标准ST= {st1,st2, … ,stn}，用于衡量所完成的过程是否达到预期效果；τ是目标状态.

定义3[9]一个资源约束是一个三元组:Res= (hr,t,f)，其中，hr描述了人力资源约束，以人月为单位；t描述了时间约束，以天为单位；f描述了资金约束，以元为单位.我们还定义针对资源约束的运算：

Res1opRes2= (Res1.hropRes2.hr,Res1.topRes2.t,Res1.fopRes2.f),op为+、-，以及资源约束之间的关系Res1reRes2当且仅当：Res1.hrreRes2.hr∧Res1.treRes1.t∧Res1.freRes1.f成立(其中re为<，>，=).

定义4 软件演化环境SEE(software evolution environment)是一个三元组:SEE=(Des,Res,Req)，其中，Des为软件演化的环境描述，Res为资源约束，Req= {Req1,Req2, …,Reqn}是一组软件演化的需求描述.

定义5 一个任务是一个四元组，task=(tid,IN,F,OUT)，其中：tid是任务的唯一标识，IN是任务的输入消息，OUT是任务执行完后的消息，F是任务具体操作，是把输入转化为输出的操作，OUT=F(IN).如果把IN作为任务要解决的问题空间，OUT当作任务的解空间，那么F就是IN和OUT之间的一个映射关系,F⊆IN×OUT.

本文中使用通讯顺序进程CSP(communicating sequential process)来对软件演化过程进行计算，且把任务当作CSP中的事件来处理，那么就存在一个事件到任务之间的转化关系，文中所采取的解决方法是：一次软件演化过程中所有任务的tid构成了本次演化过程这一客体的字母表.任务之间执行的先后顺序使用“→”来表示，a→b表示任务a执行完成后接着执行任务b.

定义7 一个活动之间的控制关系是一个四元组:R=(Activity1,Activity2,TR,c)，其中：Activity1,Activity2是2个具体的活动；TR是一个二元关系，TR⊆Activity1.T×Activity2.T，表示活动与活动之间的连接接口；c是一个连接子，c∈(C={sq,sl,lp,cn})，其中，sq表示Activity1、Activity2是顺序控制关系，sl表示Activity1、Activity2是选择控制关系，lp表示Activity1、Activity2是循环控制关系，cn表示Activity1、Activity2是并行控制关系.

定义8 过程是一个六元组:P=(A,INPUT,OUTPUT,SEE,g,R).其中：A是过程对应的行为，是一组活动的集合A= {Activity1,Activity2, …,Activityn}；INPUT和OUTPUT分别是是过程的输入信息通道集合和输出信息通道集合；SEE是过程所处的环境信息；g是过程要实现的目标；R是活动之间的控制关系.

定义9 假设存在过程SEP= (A,INPUT,OUTPUT,SEE,g,R)，SEP1= (A1,INPUT1,OUTPUT1,SEE1,g1,R1)，当且仅当条件SEE1⊆SEE∧g1g∧R1⊆R成立，称作过程p1是过程SEP的子过程，记作SEP1SEP.

2 过程的行为分析

2.1 基本结构

过程的基本结构描述了过程组合和分解关系，是进行资源计算和过程行为分析前提条件，过程的基本结构有4种，分别是顺序结构、选择结构、并行结构和循环结构，下面分别给出它们的定义:

定义10 如果过程P1，P2是顺序执行的，它们之间的顺序关系表示为：P1;P2，P1，P2的顺序表示也是一个过程，这个过程先按P1执行，在过程P1执行成功后(P1;P2)就按照P2定义的动作执行.

定义11 如果过程P1，P2只能执行其中之一，称之为程P1，P2为选择关系，记为：P1[]P2，P1[]P2的组合也是一个过程，表示实施者在实施该进程时根据环境信息做出选择，要么选择P1执行，要么选择P2执行.

定义12 如果过程P1，P2的执行都不受对方干扰，也不互为条件，则P1，P2可以并行执行，他们之间的并行关系表示为：P1||P2.

定义13 如果过程P1，P2的顺序执行有n(n>2)次，则P1，P2构成了一个n次循环结构，记作：LnP1；P2，(LnP1；P2)也是一个过程，它的入口是P1，出口是P2，这个过程先按P1执行，然后按P2执行，再按P1执行，这样重复n次.

2.2 迹

本文中的GDSEPM是基于“过程是活动的集合，活动是任务的集合”[10-11]这一观点提出的，我们把任务映射为事件来处理，所有任务的id就构成了软件演化过程的字母表，对于活动来说，其字母表就是该活动所包含的所有任务的id，对过程来说，其字母表就是该过程所包含的所有活动的字母表的并集，软件演化过程的行为是由其所包含的活动的行为组成的，所以在研究过程的行为时必须通过研究过程所包含的活动的行为来实现.由于活动是任务的集合，任务被抽象为事件来处理，活动就可以当作CSP中的进程来处理.

定义14 活动的迹是活动在执行过程中对其任务执行的一个历史记录系列，活动迹的表示为用“<”和“>”以及“，”所分割的任务tid的符号系列.

定义15 过程的迹是过程执行中对活动执行的一个历史记录，过程迹的表示为用“<”和“>”以及“，”所分割的活动aid的符号系列.

例如 过程迹S=<分析，设计，编码>分别表示3项活动分析，设计，编码，分析完成之后进入设计，设计完成后执行编码.S分析=<可行性分析，需求获取，分析与综合,制订规格说明,评审>是活动分析的迹.迹的表示沿用了进程迹的表示方法，其简单的运算也和CSP中讲述进程迹是一样的，在这里就不再重复.

过程的迹也可以细化任务级别，但在细化过程中，就要考虑过程所包含的活动之间的控制关系，为了描述方便，我们使用函数TraceP(过程名)表示获取过程的可能迹的集合，使用函数TraceA(活动名)表示获取活动的可能迹的集合.下面分别给出几种控制关系的活动的迹运算.设过程P包含活动A1，A2，则：

TraceAsq(A1,A2) = {s^t|s∈TraceA(A1)∧t∈TraceA(A2)}(顺序控制关系);

TraceAsl(A1,A2)=TraceA(A1) ∪TraceA(A2)(选择控制关系);

TraceAcn(A1,A2) = {t|tαA1∈TraceA(A2)∧tαA2∈TraceA(A1)}(并行控制关系);

TraceAlp(A1,A2)={(s^t)n|∈TraceA(A1)∧t∈TraceA(A2)}(循环控制关系).

上述规则可以推广大n(n∈N)个活动的情况，在n个活动中，先把有直接交互关系的活动使用控制关系变成一个活动，再使用该活动与其它活动使用相应的控制关系组合在一起.虽然过程是由活动组成的，但是过程的迹并不是所包含的活动迹的并集，是要通过上面的控制关系求出的.

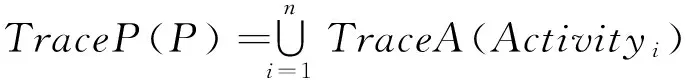
定理1可以通过活动迹的运算关系证明出来，设过程P1，P2，由它们组成的基本结构的迹的运算规则如下所示：

TraceP(P1；P2) = {s^t|s∈TraceP(P1)∧t∈TraceP(P2)}(顺序结构);

TraceP(P1[]P2)=TraceP(P1)∪TraceP(P2)}(选择结构);

TraceP(LnP1；P2) = {(s^t)n|s∈TraceP(P1)∧t∈TraceP(P2)}(循环结构).

从过程和活动的迹的运算上可以看出它们之间很相似，方法都是一样的，导致这种现象的原因是在本文中，我们把任务映射为CSP中的事件，由于活动是任务的集合，其实活动就构成了CSP中的进程，而过程的行为又是由一组活来体现的，也就是一组进程的集合，所以在运算上规则都是一样的，只是粒度大小不一样而已.

2.3 确定性和不确定性

确定性和不确定性是对过程行为的一种描述，过程的确定性和不确定性是建立在过程所包含的活动集合的行为之上的，接下来先讨论活动的确定性和不确定性.

定义16 如果一个活动A，具有以下2个属性：

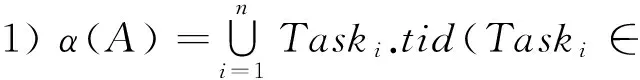
2)TraceA(A)为活动A所执行的所有可能的过程迹的集合.

如果这2个属性满足以下条件：

1) <> ∈TraceA(A)(非空性)；

2)s^t∈TraceA(A)⟹s∈TraceA(A) (前缀封闭性)；

3)TraceA(A)⊆(α(A))*.

则称活动A是确定性的，也可以说活动A是确定性活动.

或控制关系连接子“or”和选择控制关系连接子“sl”的效果是一样的，都是在2个活动中选择其中之一来执行，不同之处在于前者对环境是藏匿的，它们之间的选择是活动内部之间自己完成的，是在环境不知道或不受环境的控制之下完成的，而后者从一开始执行第一个任务时，环境就力图对其做出选择.

定义17 如果活动A里的一个任务子集X在放在某个特定的环境E中，一开始就可能死锁，就称任务集X为活动A的拒绝任务集，记作RefusalsA(A)；构成一个过程的所有活动的拒绝任务集的并集称为该过程的拒绝任务集，记作RefusalsP(过程名).

拒绝任务集在活动层的运算规则如下：

RefusalsAsq(A1,A2)={X| (X∈RefusalsA(A1)∧RefusalsA(A1) ≠∅)∨(X∈RefusalsA(A2) ∧RefusalsA(A1)=∅)}(顺序控制关系);

RefusalsAsl(A1,A2) =RefusalsA(A1) ∩RefusalsA(A2)(选择控制关系);

RefusalsAcn(A1,A2) ={X∪Y| (X∈RefusalsA(A1)∧X∈RefusalsA(A2)} (并行控制关系);

RefusalsAlp(A1,A2) ={X| (X∈RefusalsA(A1) ∧RefusalsA(A1) ≠∅)∨(X∈RefusalsA(A2) ∧RefusalsA(A1) = ∅)}(循环控制关系)

RefusalsAor(A1,A2) =RefusalsA(A1) ∪RefusalsA(A2)(或控制关系).

过程的拒绝集由该过程所包含的活动的拒绝集组成，同过程的迹的一样，也并不是简单的复合.

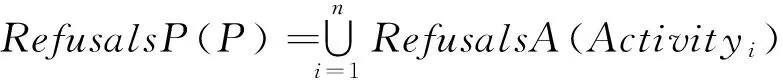
定理2的也是根据拒绝任务集在活动层的运算规则可以得出，下面的一个例子揭示了过程拒绝集的运算方法.

例1 假设存在在过程P1，P1.A={A1,A2,A3,A4}，P1.R={(A1,A2, {},sq),(A1,A3, {},sq), (A2,A3, {},cn),(A3,A4, {},sq),(A2,A4, {},sq)}，则P1.R表示的是以活动A1为开始活动并执行，执行完后并发的执行活动A2，A3，A2，A3执行完后再进入A4的执行，所以P1.R也可以表示为P1.R={(A2,A3, {},cn) ,(A1, (A2,A3, {},cn), {},sq), ((A2,A3, {},cn),A4, {},sq)}, 所以：

RefusalsAcn(A2,A3) ={X∪Y| (X∈RefusalsA(A2) ∧X∈RefusalsA(A3)}；

RefusalsAsq(A1, (A2,A3, {},cn)) = {X| (X∈RefusalsA(A1) ∧RefusalsA(A1) ≠∅)∨(X∈RefusalsAcn(A2,A3)∧RefusalsA(A1) = ∅)};

RefusalsP(P1)=RefusalsAsq((A1, (A2,A3, {},cn), {},sq),A4)=

{X| (X∈RefusalsA((A1, (A2,A3, {},cn), {},sq)) ∧RefusalsA((A1, (A2,A3, {},cn), {},sq)) ≠∅) ∨(X∈RefusalsA(A4) ∧RefusalsA((A1, (A2,A3, {},cn), {},sq)) = ∅)}=

{X| (X∈RefusalsAsq(A1, (A2,A3, {},cn))) ∧RefusalsAsq(A1, (A2,A3, {},cn)) ≠∅) ∨(X∈RefusalsA(A4) ∧RefusalsAsq(A1, (A2,A3, {},cn)) = ∅)}.

由上面的计算可以看出，某一个具体过程的拒绝集是通过其内部活动的拒绝集运算而得到的，在过程层次几种过程基本结构的拒绝任务集也是由其参与运算的象过程的拒绝集的并集，即：

RefusalsP(P1；P2) =(X| (X∈RefusalsP(P1) ∧RefusalsP(P1) ≠∅) ∨(X∈RefusalsP(P2) ∧RefusalsP(P1) = ∅)(顺序结构);

RefusalsP(P1[]P2) =RefusalsP(P1) ∩RefusalsP(P2)(选择结构);

RefusalsP(LnP1；P2)=(X|(X∈RefusalsP(P1) ∧RefusalsP(P1) ≠∅) ∨(X∈RefusalsP(P2) ∧RefusalsP(P1) = ∅) (循环结构);

仿照CSP对过程确定性的讨论[12],对软件演化过程中的活动和过程做相应讨论，对于确定性活动来说，它是不能拒绝它能执行的任何任务，换句话说，一个任务的集合为某个确定性活动的拒绝集，当且仅当该任务集合不包含该活动最初能执行的即任务，即：

(活动A是确定的)⟹ (X∈RefusalsA(A)≡(X∩A0={})，其中A0=(x|∈TraceA(A)).

对于活动A执行了任何任务系列以后，该条法则同样适用，即：

(活动A是确定的)≡ (∀s:TraceA(A).(X∈RefusalsA(A/s)≡(X∩((A/s))0={})).

同样的道理，对于过程来说，也有：

(过程P是确定的) ⟹ (Y∈RefusalsP(P)≡(Y∩P0={})，其中P0=(x| ∈TraceP(P) )；

(过程P是确定的)≡ (∀s:TraceP(P).(Y∈RefusalsP(P/s)≡(Y∩((P/s))0={})).

从过程、活动的拒绝集运算上可以看出，其基本结构和基本控制关系的拒绝集的运算规则表达方式是一样的，导致这种现象产生的原因是由于过程是由活动构成的，在研究软件演化过程的行为之时，撇开过程的目标和环境，过程其实也就是一个粒度更大的活动而已.

一般说来，在软件的演化过程中，不同角色、组织所关心的软件演化的粒度是不一样的，譬如项目经理并不关心模块A的代码如何编写、什么时候写？他的关注点通常粒度较大，他并不关心每一个具体的任务细节，所以我们引入了屏蔽算子“”，它的运算结果是屏蔽掉活动或过程里的一些任务，这是非常有用的，比如在过程的层面，我们关注的是各个过程之间的依赖关系，并不需要知道具体的实现细节和内部结构的，其里面的任务是不受外部环境的观察和控制的.就可以使用算子“”对一些任务进行屏蔽，“”算子的格式为：

活动{任务tid的集合}，过程{任务tid的集合}

对于过程来说，还可以进一步屏蔽掉某些活动，格式为：过程{活动aid的集合},设过程P，P.A= {Activity1,Activity2, … ,Activityn}，

即屏蔽掉一个活动就等于把该活动里所有的任务屏蔽掉，同理如果屏蔽掉多个活动时，就等于把这几个活动的任务并集给屏蔽掉，即：

设T是需要被屏蔽掉的任务的有限集合，则PT为一个似P的过程，AT是一个似A的活动，只是P和A内部执行的任务如果出现在T中都被屏蔽掉了.显然有：

α(PT) =α(P)-T，α(AT) =α(A)-T.

(μX·(c→X[]e→c→P)，在对任务c进行屏蔽运算后：

在引入屏蔽算子后，会导致原本卫式表示的过程行为变为非卫式形式，使其解不唯一，比如存在一个递归的过程行为：P=a→P，对任务a实施屏蔽操作后变为P{a} =P{a}，相当于定义了一个方程x=x，这是一个具有无穷多个解的方程，对于出现这种情况，文中规定其最不确定的那个解就是所要求解的解，这样就可以甩掉卫式的限制条件，而且可以给形式为μX·F(X)的每个表达式赋予含义.

定义18 如果在活动中，出现形如μX·X的活动行为，那么就会导致该活动的行为是最不确定的，是最难预测、最难控制的，我们把具有这种性质的活动称之为活动浑沌，把包含有活动浑沌的过程称之为过程浑沌.显然一个浑沌过程是无用的，记为CHAOSαName，Name为活动名或过程名.

其实，在建模之初的初始过程就可以看作是一个浑沌过程，因为对于初始过程来说，里面的活动和任务都是杂乱无章的，人们根本不清楚如何去实施演化，从哪里入手.

定义19 如果某个活动A的行为在执行完某一个迹s之后，剩余的任务就进入了一个混沌状态，就称s为活动A的一条发散迹，由多条这样的s组成的集合称为活动A的发散迹集，记作DivergencesA(A)，过程里面所有活动的发散迹集所构成集合称为该过程的发散迹集，记作DivergencesP(P).

DivergencesA(A) = {s|s∈TracesA(A)∧ (A/s) =CHAOSαA}.

在活动层次几种基本控制关系的发散迹集的运算关系如下：

DivergencesAsq(A1,A2) =DivergencesA(A1) ∪ {s^t|s∈TraceA(A1)∧t∈DivergencesA(A2)}(顺序控制关系);

DivergencesAsl(A1,A2) =DivergencesA(A1) ∪DivergencesA(A2)(选择控制关系);

DivergencesAcn(A1,A2) ={s^t|t∈(αA1∪αA2)*∧ ((sαA1∈DivergencesA(A1) ∧sαA2∈TraceA(A2)) ∨(sαA1∈TraceA(A1) ∧sαA2∈DivergencesA(A2))}(并行控制关系);

DivergencesAlp(A1,A2) =DivergencesA(A1)∪{s^t| (s∈ (TraceA(A1) ∪(TraceA(A2))*∧t∈ (DivergencesA(A1) ∪DivergencesA(A2))}(循环控制关系);

DivergencesAor(A1,A2)=DivergencesA(A1) ∪DivergencesA(A2) (或控制关系).

同拒绝集一样，过程的发散迹集同样不是简单的把过程中所包含的各个活动的发散迹集简单的合并在一起，即：

定理3 在一个含有n(n>2)个活动{Activity1,Activity2, …,Activityn}组成的过程P中，当且仅当这些活动之间的关系仅存在或控制关系和选择控制关系时：

定理3也可以根据发散迹集在活动层的运算规则得出，以例1的过程P1为例来计算过程的发散迹集，计算过程如下.

DivergencesAcn(A2,A3) = {s^t|t∈(αA2∪αA3)*∧ ((sαA2∈DivergencesA(A2) ∧sαA2∈TraceA(A3)) ∨(sαA2∈TraceA(A2) ∧sαA3∈DivergencesA(A3))};

DivergencesAsq(A1, (A2,A3, {},cn)) =DivergencesA(A1) ∪ {s^t|s∈TraceA(A1) ∧t∈DivergencesAcn(A2,A3)};

DivergencesP(P1) =DivergencesAsq((A1, (A2,A3, {},cn), {},sq),A4)=

DivergencesAsq(A1, (A2,A3, {},cn)) ∪ {s^t|s∈TraceAsq(A1, (A2,A3, {},cn)) ∧t∈DivergencesA(A4)}=DivergencesA(A1) ∪ {s^t|s∈TraceA(A1) ∧t∈DivergencesAcn(A2,A3)} ∪ {s^t|s∈

TraceAsq(A1, (A2,A3, {},cn)) ∧t∈DivergencesA(A4)}.

同样的，在过程层次中，过程的几种基本结构的发散迹集的运算关系如下所示，其结构和在活动层的几种基本控制关系的运算是一样的，具体的原因在描述拒绝集的运算关系时已经说明，在此不再重复.

DivergencesP(P1；P2) =DivergencesP(P1) ∪ {s^t|s∈TraceP(P1) ∧t∈DivergencesP(P2)}(顺序结构);

DivergencesP(P1[]P2)=DivergencesP(P1)∪DivergencesP(P2) (选择结构);

DivergencesP(P1||P2) ={s^t|t∈(αP1∪αP2)*∧ ((sαP1∈DivergencesP(P1) ∧sαP2∈TraceP(P2)) ∨ (sαP1∈TraceP(P1) ∧sαP2∈DivergencesP(P2))} (并行结构);

DivergencesP(LnP1；P2)=DivergencesP(P1) ∪{s^t| (s∈ (TraceP(P1)∪ (TraceP(P2))*∧t∈(DivergencesP(P1) ∪DivergencesP(P2))}(循环结构);

在给出以上定义的基础之上，还有一个重要的定义要给出，那就是绝境集[13]，绝境集描述的不仅是活动或过程一开始就拒绝执行的任务，还描述了继迹s之后可能的拒绝集，所以绝境集是一个迹和一个任务集的二元关系的集合.

定义20 绝境是一个二元关系failure=，其中s是活动或过程的迹，X是活动或过程在执行完s中的任务后的拒绝集，活动的绝境集表示为FailuresA(Activity)，过程的绝境集表示为FailuresP(Process).

由上述定义可知，活动的绝境集和过程的绝境集分别为：

FailuresA(Activity) = {|s∈TraceA(Activity)∧X∈RefusalsA(Activity/s)};

FailuresP(Process) = {|s∈TraceP(Process) ∧X∈RefusalsP(Process/s)}.

接下来，我们同样给出绝境集分别在活动层和过程层上的运算关系，在活动层次几种基本控制关系的绝境集的运算关系如下：

FailuresAsq(A1,A2) =FailuresA(A1) ∪{ |s∈TraceA(A1) ∧∈FailuresA(A2)}(顺序控制关系);

FailuresAsl(A1,A2)={|∈(FailuresA(A1)∩FailuresA(A2)) ∨(s≠ <>∧ ∈(FailuresA(A1) ∪FailuresA(A2)))}∪{|s∈DivergencesAsl(A1,A2)} (选择控制关系);

FailuresAcn(A1,A2) ={|s∈(αA1∪αA2)*∧∈FailuresA(A1)∧∈FailuresA(A2)} ∪{|s∈DivergencesAcn(A1,A2)}(并行控制关系);

FailuresAlp(A1,A2) =FailuresA(A1) ∪ { |s∈ (TraceA(A1)∪TraceA(A2))*∧∈FailuresA(A2)}(循环控制关系);

FailuresAor(A1,A2) =FailuresAsl(A1,A2)(或控制关系).

FailuresAcn(A2,A3) ={|s∈(αA1∪αA2)*∧∈FailuresA(A2)∧ ∈FailuresA(A3)} ∪{|s∈DivergencesAcn(A2,A3)};

FailuresAsq(A1, (A2,A3, {},cn)) =FailuresA(A1) ∪ { |s∈TraceA(A1) ∧∈FailuresAcn(A2,A3)};

FailuresP(P1) =FailuresAsq((A1, (A2,A3, {},cn), {},sq),A4) =

FailuresAsq(A1, (A2,A3, {},cn)) ∈{ |s∈TraceAsq(A1, (A2,A3, {},cn)) ∧∈FailuresA(A4)}=FailuresA(A1) ∪ { |s∈TraceA(A1)∧ ∈FailuresAcn(A2,A3)} ∪

{ |s∈TraceAsq(A1, (A2,A3, {},cn)) ∧∈FailuresA(A4)}.

在活动层次几种基本结构绝境集的运算关系如下：

FailuresP(P1;P2) =FailuresP(P1) ∪ { |s∈TraceP(P1) ∧∈FailuresP(P2)}(顺序结构);

FailuresP(P1[]P2)={|∈(FailuresP(P1)∩FailuresP(P2))∨ (s≠ <> ∧∈(FailuresP(P1)∪FailuresP(P2)))}∪{|s∈DivergencesPsl(P1,P2)} (选择结构);

FailuresP(P1||P2) ={|s∈(αP1∪αP2)*∧ ∈FailuresP(P1) ∧∈FailuresA(P2)} ∪{|s∈DivergencesPcn(P1,P2)}(并行结构);

FailuresP(LnP1；P2) =FailuresP(P1) ∪{|s∈ (TraceP(P1)∪TraceP(P2))*∧∈FailuresP(P2)}(循环结构);

至此，我们回过去看定义6中定义活动时的F和Div，在给出以上这些概念的基础之上就可以清晰地对F和Div进行描述，其实F和Div所表示的分别是绝境集合发散迹集.在此基础之上就可以给出确定性过程和不确定性过程的定义.

定义21 如果过程的行为不包括任何不确定性的因素，则称该过程是确定性过程，反之称为不确定性过程.

3 结语

本文对面向目标导向的软件演化过程的行为进行了深入细致的分析，以软件演化过程的迹为基础，引出了过程的发散、绝境等问题，并给出了相应求解办法，对演化过程的行为进行分析，有助于在演化工作开始之前发现不合理的设计，以便尽早修改从而降低软件演化的风险.在过程的行为分析中，对过程的确定性、不确定性、发散性和绝境4个方面，分别从活动层和过程层进行讨论.在接下来的工作中，将要建立对应的模型验证规则来对模型进行验证.

[1] LEHMAN M M. Laws of software evolution revisited[M]//Software Process Technology. Berlin Heidelberg:Springer, 1996: 108-124.

[2] 单银根,王安,黎连业. 软件能力成熟度模型 (CMM) 与软件开发技术[M]. 北京：北京航空航天大学出版社, 2003.

[3] OSTERWEIL L. Software processes are software too[C]//Proceedings of the 9th International Conference on Software Engineering. IEEE Computer Society Press, 1987: 2-13.

[4] EL EMAM K, BIRK A. Validating the ISO/IEC 15504 measure of software requirements analysis process capability[J]. Software Engineering, IEEE Transactions on, 2000, 26(6): 541-566.

[5] KAHEN G, LEHMAN M M, RAMIL J F, et al. Dynamic modelling in the investigation of policies for E-type software evolution[C]//Proceedings of the Software Process Simulation Modeling Workshop ,ProSim 2000.

[6] 李长云. 软件动态演化技术[M].北京：北京大学出版社, 2007.

[7] LI T. An approach to modelling software evolution processes[M]. Berlin: Springer, 2008.

[8] 吴骏, 王崇骏, 骆斌, 等. Agent 主动目标的形式化模型[J]. Journal of Software, 2008, 19(7): 1644-1653.

[9] 赵欣培, 李明树, 王青, 等. 一种基于 Agent 的自适应软件过程模型[J]. 软件学报, 2004, 15(3): 348-359.

[10] IEEE standard for developing software life cycle processes[S]. IEEE Standard 1074—1991,1997.

[11] The international organization for standardization (ISO) and the international electro technical commission (IEC)[S]. (ISO/IEC 12207) Standard for Information Technology-Software Life Cycle Processes, 1998.

[12] HOARE C A R.通信顺序进程[M]. 周巢尘，译．北京：北京大学出版社, 1990.

[13] IEEE recommended practice for software requirements specifications[S]. IEEE Std 830—1998,1998.

[14]李超，谢冲武. 软件需求分析方法研究进展[J].湖北民族学院学报，2013，31(2)：204-211.

(责任编辑 庄红林)

Study of the goal-directed software evolution process

HUANG Shi-fan1,SHEN Yong1,2,WANG Dao-hong3,KANG Hong-wei1，2,ZHENG Jian-lin1,JIA Shu-wei1

(1.School of Software, Yunnan University, Kunming 650091, China;2.Key Laboratory for Software Engineering of Yunnan Province, Yunnan University, Kunming 650091, China;3.Center of Science and Technology for Settlement, Rural Credit Cooperatives of Yunnan Province, Kunming 650000, China)

Analyses of the evolution process of the software can help discover some unreasonable designs and improve them earlier, thus reducing the software evolution risk. On the base of the goal-directed software evolution process, this research follows the principle of the communicating sequential process to give an incisive analysis of the software process. This paper analyzes the process trace, the process certainty and uncertainty respectively，and gives the calculation method of every kind of process.

communicating sequential process;goal-directed;software evolution process;process behavior

2014-03-07.

云南省软件工程重点实验室面上基金(2012SE306;2011SE12).

黄世反(1988-)，男，硕士研究生. 主要研究方向：软件工程.

沈 勇(1970-)，男，硕士,副研究员.主要研究方向：信息系统分析与集成、软件工程与工程环境.

TP31

A

1672-8513(2015)01-0066-09