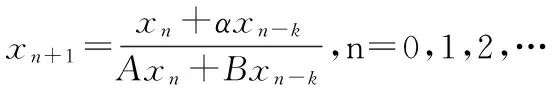一类高阶有理差分方程的全局渐近稳定性
张永玲
(兰州交通大学 数理学院,甘肃 兰州 730070)
一类高阶有理差分方程的全局渐近稳定性
张永玲
(兰州交通大学 数理学院,甘肃 兰州 730070)
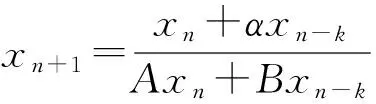
正平衡点;不变区间;全局吸引子;全局渐近稳定
研究有理差分方程
(1)
通过变量变换xn=βyn转化为
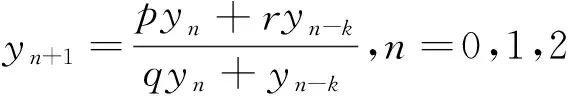
(2)
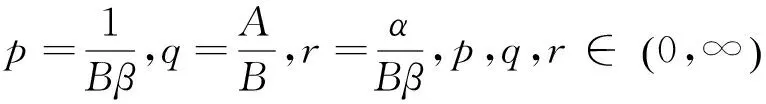
下文主要研究方程(1)的全局渐近稳定性.
1 预备知识
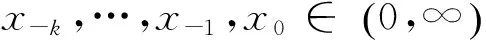
(3)
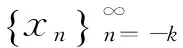
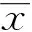
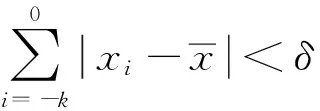
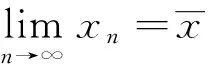
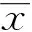
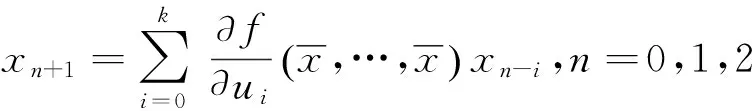
它的特征方程是
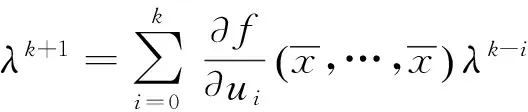
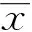
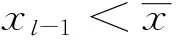
且
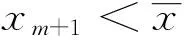

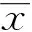
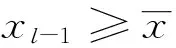
且
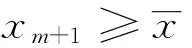

引理1 对于差分方程

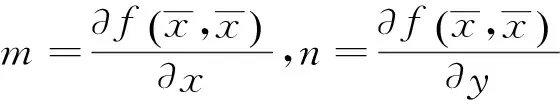
则
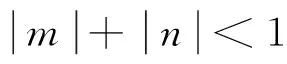
是方程
xn+1=mxn+nxn-k,n=0,1,2,…,
局部渐近稳定性成立的充分条件.
引理2 考虑差分方程

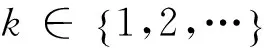
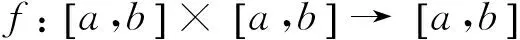
满足以下条件
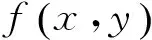

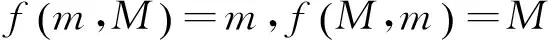
2 主要结论
设
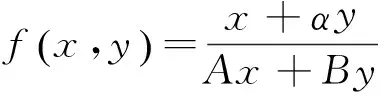
则有
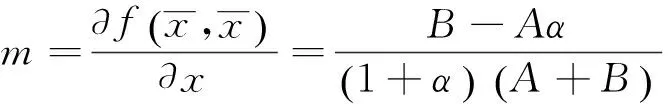
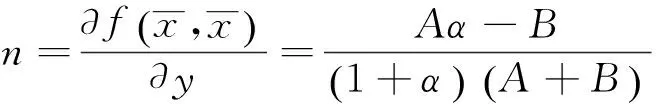
可得到m=-n.
由定义3知,方程(3)在平衡点处的线性方程为
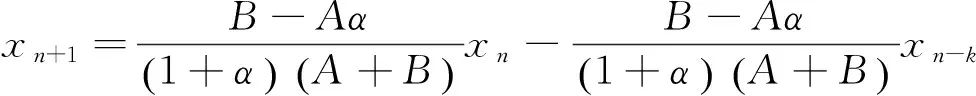
特征方程为

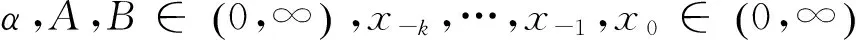
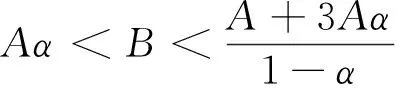

证明:

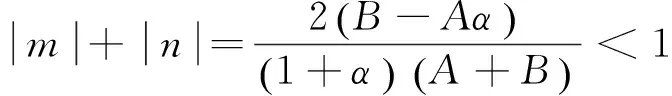

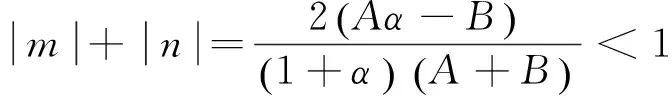
(4)
定理证毕.
定理2 方程(2)有正的素二周期解.
证明:以下将考虑方程(2)的正的素二周期解.令…,φ,ψ,φ,ψ,…是方程(2)的一个素二周期解,φ和ψ是2个不相同的正整数.
如果k是偶数,那么yn=yn-k,则φ和ψ满足以下条件
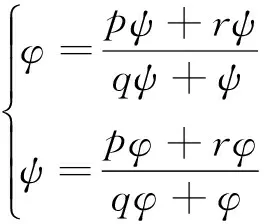

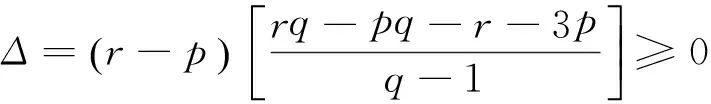
1) 若q-1<0,则φψ<0,无非负素二周期解,故舍去;
2) 若q-1>0,则rq-pq-r-3p≥0,方程(2)有素二周期解.
综上所述,当且仅当k是奇数,rq-pq-r-3p≥0时,方程的素二周期解存在且唯一.
定理3 方程(2)的所有正解都有界.
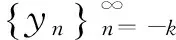
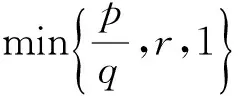
对所有n≥0成立.
然后
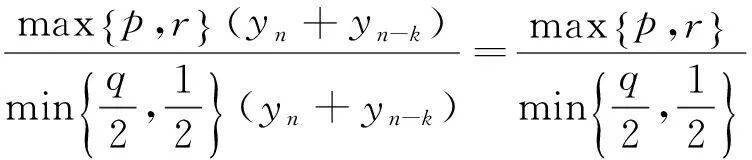
对所有n≥k成立.定理得证.
定理4 (a)假设B≥Aα,f(x,y)那么是对每一个y关于x是递增的,且f(x,y)对每一个x关于y是递减的;

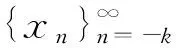
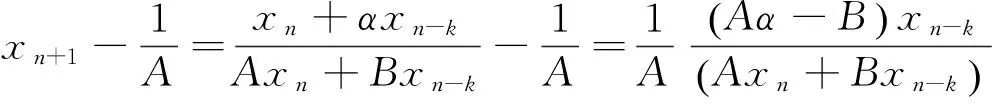
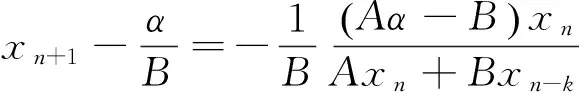
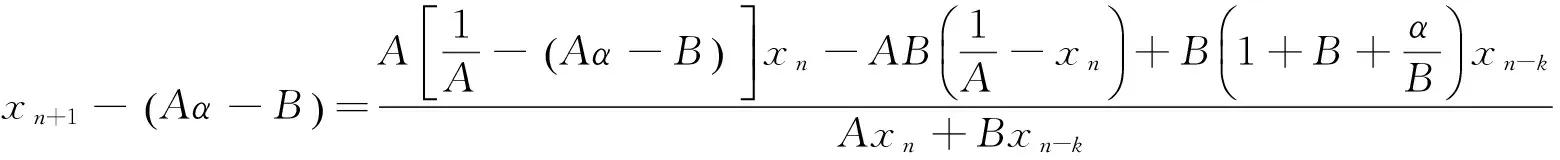

(5)
根据上面的结论和定义4,得到下面的引理.
引理3 假设
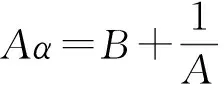
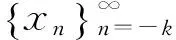
定理5 方程(1)有以下不变区间:
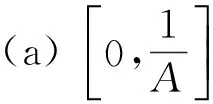
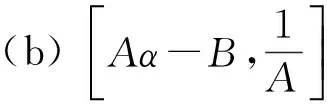
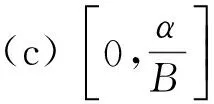
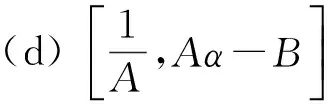

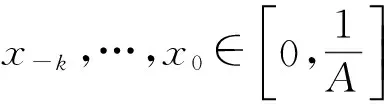
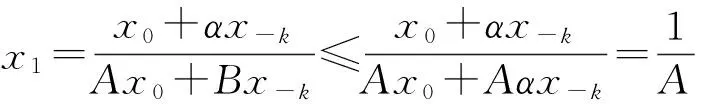
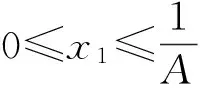
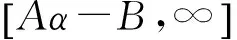
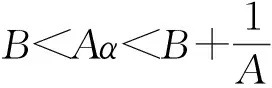
得到

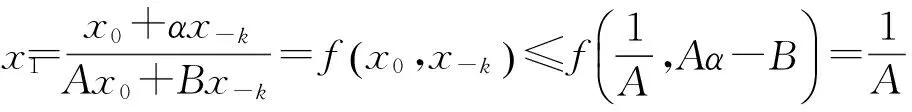
故
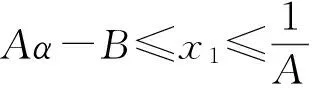
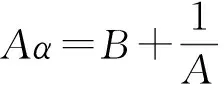
有

故
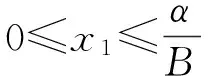
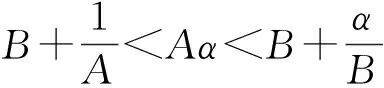
有
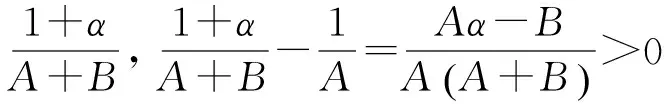
故
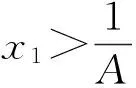
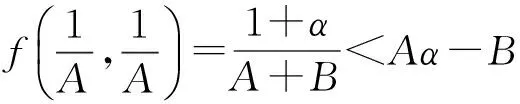
所以
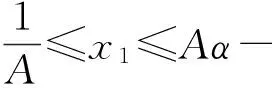
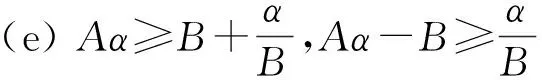
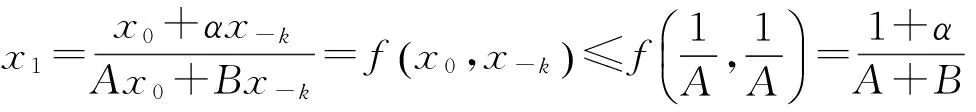
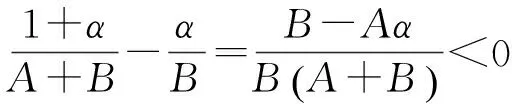
故
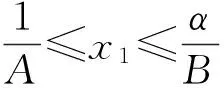
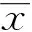
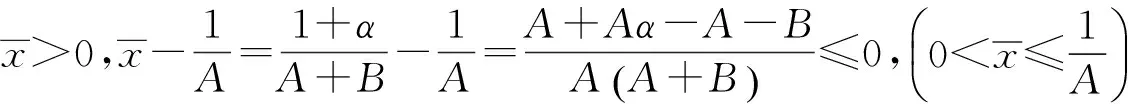
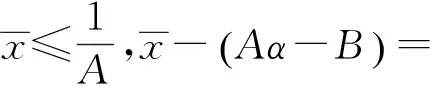
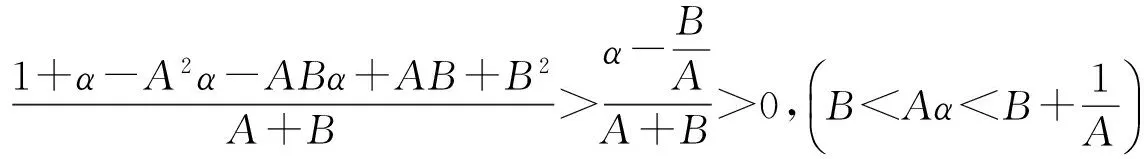

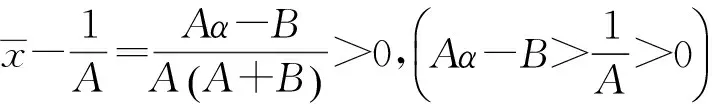
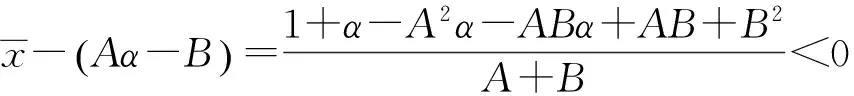
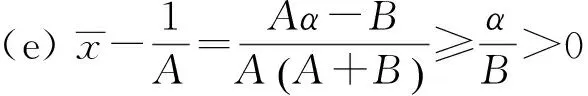
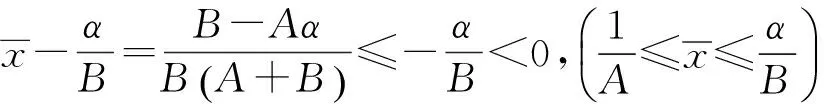
下面讨论方程(1)的全局渐近稳定性
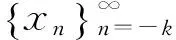
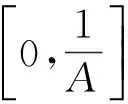
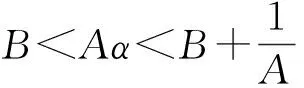
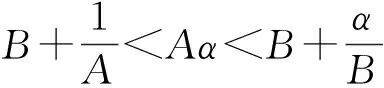
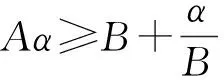
以下讨论由引理4得出的5种情形下的全局吸引子.
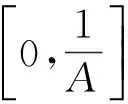
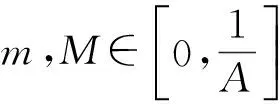
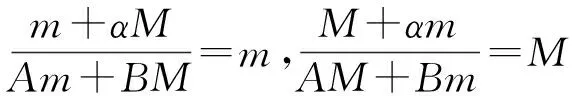
等价于
Am2+BmM=m+αM,
AM2+BmM=M+αm,
则

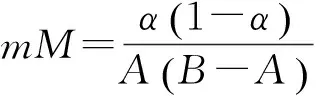
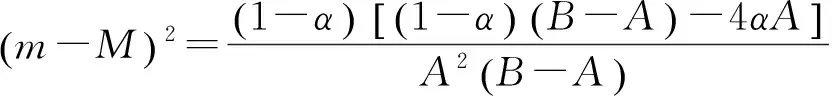
又由
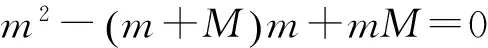
得到
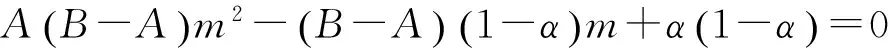
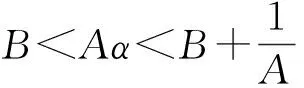
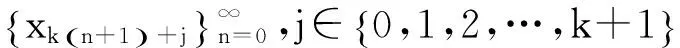

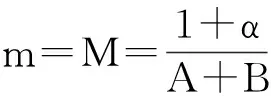
根据定义2,定理1和定理6,得到下面的定理:
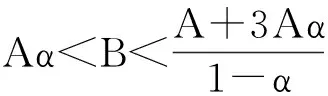

[1]KULENOVICMRS,LADASG,PROKUPNR.Arationaldifferenceequation[J].ComputersandMathematicswithApplications,2001(41): 671-678.
[2]TANGGuo-mei,HULi-xia,JIAXiu-mei.Dynamicsofahigher-ordernonlineardifferenceequation[J].DiscreteDynamicsinNatureandSociety, 2010,ArticleID534947.
[3]JIAXiu-mei,LIWan-tong.Boundednessandglobalattractivityofahigher-ordernonlineardifferenceequation[J].DiscreteDynamicsinNatureandSociety, 2010,ArticleID610467.
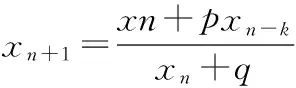
[5] DEHGHAN M, MAZROOEI-SEBDANI R.Dynamics of high-order rational difference equation[J].Applied Mathematics and Computation,2006,178:345-354.
[6] JIA Xiu-mei,HU Liu-xia,LI Wan-hong.Dynamics of a rational difference equation [J]. Discrete Dynamics in Nature and Society,2010,Aeticle ID 970720.
[7] DEHGHAN M, RASTEGAR N.On the global behavior of a high-order rational difference equation[J].Computer Physics Communications,2009, 180 (6): 873-878.
[8] 梁璐莎,陈斯养.中立型Logistic差分方程的Flip分支[J].云南师范大学学报:自然科学版,2014,34(1):41-47.
(责任编辑 梁志茂)
The global asymptotic stability of a higher-order difference equation
ZHANG Yong-ling
(School of Mathematics and Physics, Lanzhou Jiaotong University,Lanzhou 730070, China)
This paper investigates the local stability,prime period-two solutions,boundedness,invariant intervals,and the global asymptotic stability of all positive solutions of the following difference equation
positiveequilibriumpoint;invariantintervals;globalattractor;globalasymptoticstability
2014-03-06.
国家自然科学基金(11461039,11061018);国家自然基金甘肃省级联合基金(1212RJZA043);陇原青年创新人才支持计划(252003);兰州交通大学青年基金(2011028).
张永玲(1988-),女,硕士研究生. 主要研究方向:计算数学.
O
A
1672-8513(2014)06-0037-06