基于LMI的工业控制仿真器的H∞鲁棒PID控制器设计

王佳伟，杨亚非，钱玉恒，赵新宇

（哈尔滨工业大学飞行器控制实验教学中心，黑龙江哈尔滨 150001）

基于LMI的工业控制仿真器的H∞鲁棒PID控制器设计

王佳伟，杨亚非，钱玉恒，赵新宇

（哈尔滨工业大学飞行器控制实验教学中心，黑龙江哈尔滨 150001）

推导了工业控制仿真器的数学模型，将工业控制仿真器配置为一个二阶的刚体对象。使用极点区域配置和H∞性能指标，并且利用线性矩阵不等式这一强大的数学工具，为其设计了鲁棒PID控制器，进行了仿真验证，得到的仿真结果表明了所设计控制器的有效性。

线性矩阵不等式；工业控制仿真器；PID控制器；鲁棒性控制器

控制系统的鲁棒性是指系统参数发生变化或有干扰信号作用时仍可使控制效果保持不变的性能。普通PID控制器是以固定的PID参数去适应被控过程中的不确定性因素，鲁棒性较差，很难获得令人满意的控制效果。线性矩阵不等式（linear matrix inequality，LMI）是一种近年来被广泛使用的很有效的数学工具，特别是Matlab的LMI工具箱提供了数值求解线性矩阵不等式的工具，使得对线性矩阵不等式的求解更加方便。在控制领域中，由于许多问题都能转化为线性矩阵不等式的可解性问题，或者具有线性矩阵不等约束的优化问题，因此，LMI工具箱已经成为解决控制问题、提高PID控制器鲁棒性的一个极其重要数学工具［1－2］。

工业控制仿真器是一个综合实验平台，可以仿真单轴仿真转台［3－5］、主轴传动机械［6］、传送带［7－8］、数控机床［9－10］、自动装配生产线［11－12］等工业生产设备，可以模拟这些设备的控制性能，包括加入摩擦、齿轮间隙变化［13－14］和干扰后系统的响应性能。本文将工业控制仿真器简化为刚体模型，利用LMI方法设计H∞鲁棒PID控制器。通过这一过程，学生能够了解和掌握工业仿真器的控制原理及先进的控制算法。

1 区域极点配置

控制系统的动态响应主要是由其极点配置决定的，把极点配置在一些特定的区域内，可以获得较好的控制性能，因此这些区域能够决定系统的一些指标。如果存在一个对称的实矩阵L和一个实数矩阵M，使得复平面的子区域D＝，那么D就称为LMI区域［15］，则定义区域D的特征函数为：

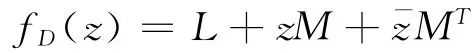
下面给出几种典型的LMI区域。

（1）直线区域。

其中，α＞0为某个正实数，并且上式等价于Re（z）＜－α，其中Re（z）表示复数z的实部，说明该区域是以直线Re（z）＜－α为边界的左半复平面。（2）圆盘区域。

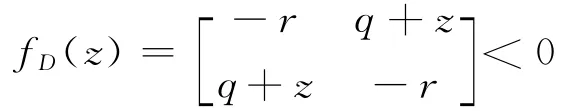
其中，圆盘区域的圆心位于点（－q，0），圆盘区域的半径大小为r。

（3）扇形区域。

其中，扇形区域的顶点为坐标系的原点（0，0），区域的扇角为2θ。

本文中将要考虑的复平面子区域是由上述直线区域、圆盘区域和扇形区域包围形成的，将该区域记为S（α，r，θ）。

2 基于LMI的H∞鲁棒PID控制器

2．1 控制器约束

图1所示为闭环控制框图。

图1 控制系统结构图

图中r为参考输入，e为偏差，u为控制输入，w为零均值高斯白噪声信号，y为输出；G（s）表示完全能观的被控对象的传递函数：

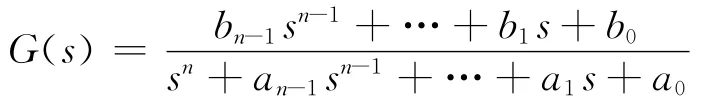
C（s）为控制器，采用如下PID控制器的形式：

其中P、I、D三个参数是关于滤波器参数ε的函数。

G（s）的状态空间表示形式为：

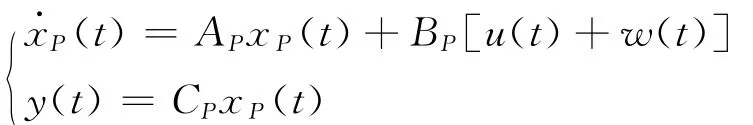
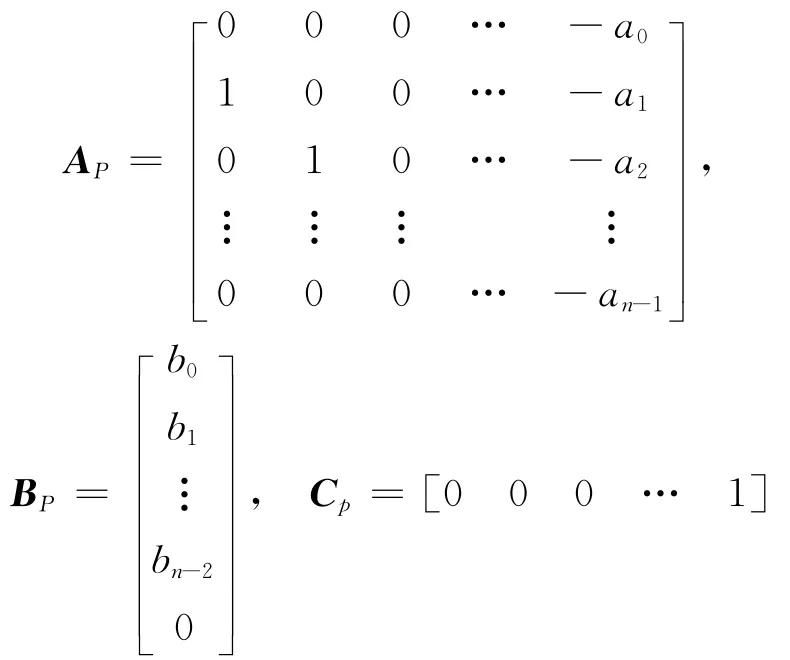
式中：假定系统的参考输入为零，则有

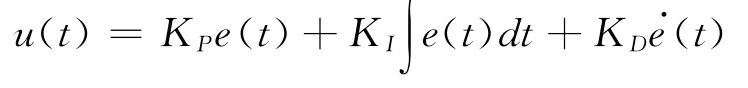
由此可得闭环系统的方程为：

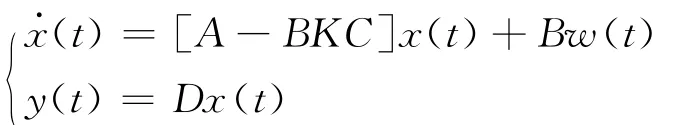
并且假设闭环系统的初始状态x（0）与w（t）不相关。

至此，鲁棒PID控制器的设计问题可转化为当系统满足约束1——闭环系统A－BKC的极点分布在复平面的区域S（α，r，θ）中和约束2——从扰动w到被控输出的传递函数矩阵满足‖H（s）‖’＜γ时，求取控制器参数Kp、KI、KD值的问题。

2．2 PID控制器参数整定

如果矩阵变量为［S1，Q11，Q22］的下列线性矩阵不等式有解［1］：

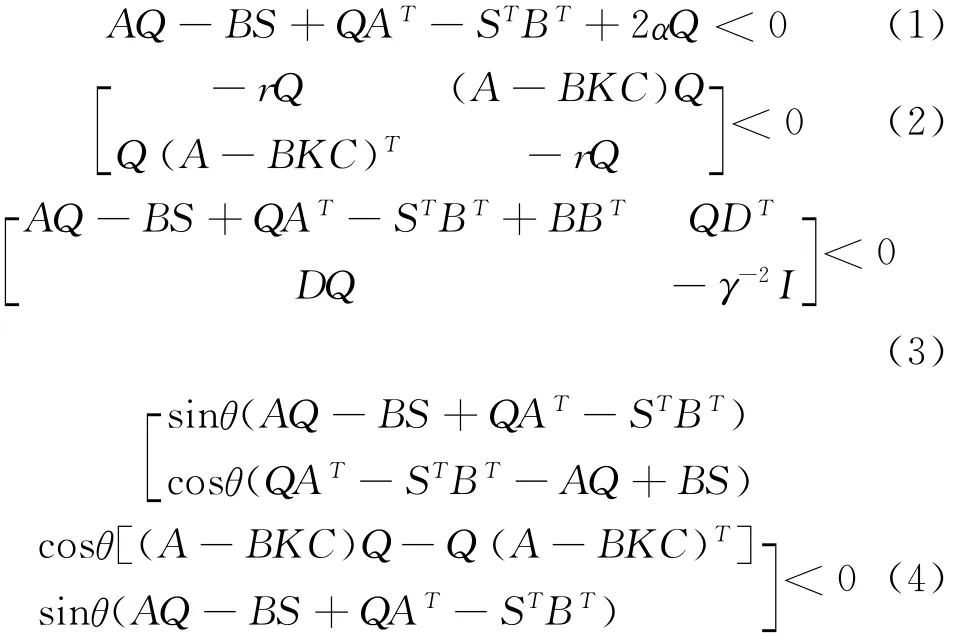
式中：

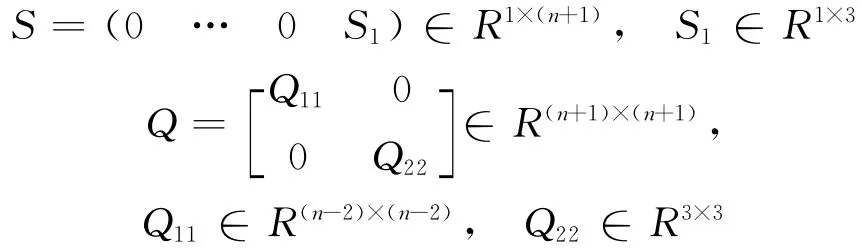
则PID控制器参数为：

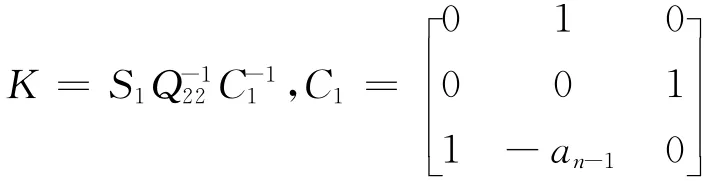
3 工业控制仿真器组成及数学模型介绍

3．1 结构和组成

工业控制仿真器由3个子系统组成：（1）装置机械部分（见图2）；（2）由DSP处理器构成的控制系统，用来执行控制律，该控制器可以解释指令，支持数据采集、轨迹描绘、系统状态及安全检测功能；（3）执行软件，即系统的用户界面，它支持控制器的选择和构建、输入轨迹定义、输出数据收集、绘图等系统操作。

3．2 机械部分和数学模型

工业控制仿真器的机械部分如图2所示。机械部分包括2个可调惯量的圆盘：一个是驱动圆盘，由伺服电机通过皮带驱动；另一个是负载圆盘，通过皮带、齿轮组驱动。负载圆盘与驱动圆盘均可通过加载、卸载砝码或者改变砝码的位置来调整惯量。传动齿轮组的齿轮间隙和减速比可以改变，从而实现多种模型的配置。

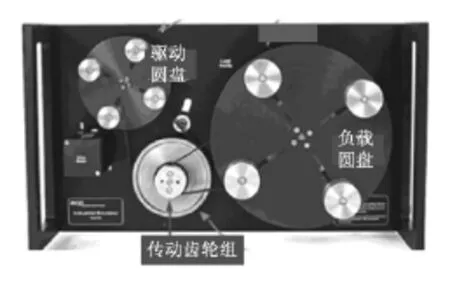
图2 机械部分

如果忽略机械传动中的柔性、齿隙等一些非线性因素的影响，系统可以近似看作刚体，并且假设考虑的摩擦是黏性的，只考虑驱动圆盘，根据图3的受力分析，可得到

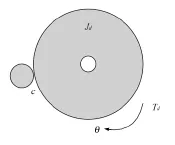
图3 受力分析

传递函数为

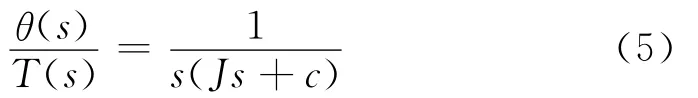
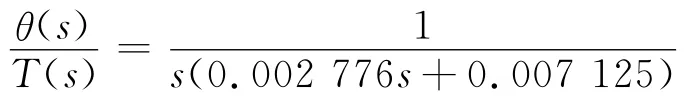
4 控制器参数设计及仿真验证

取上节推导的工业控制仿真器的数学模型，同时考虑装置引入的硬件增益Khw＝5．81，则系统传递函数为

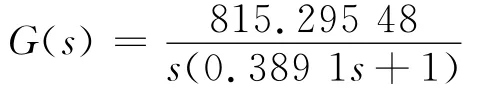
取

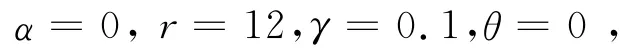
反馈控制器的形式取为

根据上一节的分析推导，可知：

将A、B、C、D代入式（1）—式（4）中，利用Matlab中的LMI工具箱进行求解，可解得矩阵变量为：

解得PID控制器参数为

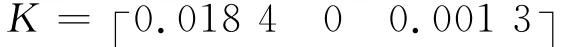
分析系统的闭环极点为－0．884 58和－146．354 62，系统的闭环极点的实部全部是负值，说明该闭环系统稳定。

在Model－220上进行实验验证，得到的跟踪阶跃信号曲线如图4所示。由图可以看出，控制曲线在整个控制过程中表现较为平稳，超调量很小，上升时间短，此系统不仅稳定，而且还具有非常好的性能指标。

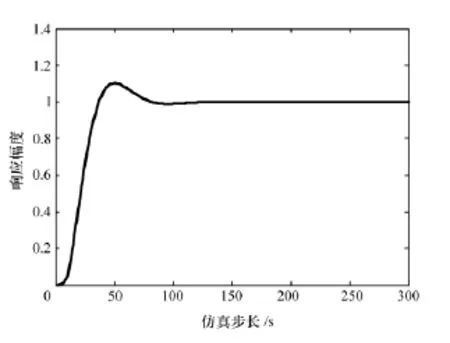
图4 仿真结果

5 结束语

通过仿真验证说明，基于LMI的工业控制仿真器的PID控制器具有很好的鲁棒性。通过这个实验教学过程，学生可以加深对先进控制方法的理解，为进一步学习工业控制课程打下基础。

（References）

［1］郑泳凌，马龙华，钱积新．鲁棒PID控制器参数整定方法［J］．化工自动化及仪表，2001，28（5）：14－16．

［2］李会军，陈明军．基于LMI的H∞鲁棒PID控制器设计［J］．控制工程，2007，14（3）：294－296．

［3］邓正隆，王爽．陀螺漂移测试转台的发展和展望［J］．宇航学报，1987（3）：91－95．

［4］宋桂云．常用陀螺测试系统［J］．有色金属，2005（2）：128－130．

［5］吴南江．一种单轴测试转台设计［J］．伺服控制，2007（11）：61－62．

［6］杨金鹏，尹存涛，章鸿，等．全齿轮传动主轴的软起节能运行制动器设计［J］．新技术新工艺，2012（12）：63－65．

［7］朱立平，韩东劲，许静泉．输送带的动力学模型［J］．煤矿机械，2001（2）：29－30．

［8］周广林，陈健，罗凤利，等．输送带的粘弹力学特性［J］．煤矿机械，2001（12）：22－24．

［9］李军锋，李剑，席平．数控机床加工仿真技术及应用［J］．计算机仿真，2003，20（4）：92－94．

［10］孔杰，覃岭．数控车床主轴传动系统的动力学优化设计［J］．机械传动，2012，36（7）：59－61．

［11］谢永宏，朱梅，李绍炎，等．自动装配生产线教学演示系统设计研制［J］．深圳职业技术学院学报，2004（2）：30－33．

［12］强小拾，罗庚合．机电一体化自动装配教学生产线的应用［J］．西安航空技术高等专科学校学报，2009，27（3）：63－65．

［13］李丹．传动装置齿隙位置对伺服系统的影响［J］．重型机械科技，2004（2）：26－31．

［14］周金柱，段宝岩，黄进．含有齿隙伺服系统的建模与对开环频率特性的影响［J］．中国机械工程，2009，20（14）：1722－1725．

［15］Ahmoud C，Pascal G．H∞Design with Pole Placement Constraints：An LMI Approach［J］．IEEE Transctions on Automatic Control，1996，41（3）：358－367．

Design of H∞robust PID controller for industrial control emulator based on linear matrix inequality（LMI）

Wang Jiawei，Yang Yafei，Qian Yuheng，Zhao Xinyu
（Experiment and Teaching Center for Flight Vehicle Control，Harbin Institute of Technology，Harbin 150001，China）

The mathematical model of industrial control emulator is derived and configured as a rigid body object with two orders．Using the method of regional pole placement and H∞performance with linear matrix inequality（LMI），a robust PID controller is designed．After simulation based on industrial control emulator，the effectiveness of the designed controller is shown．

linear matrix inequality（LMI）；industrial control emulator；PID controller design；robust control－ler

TP271

A

1002－4956（2015）3－0137－04

2014－07－02 修改日期：2014－12－26

黑龙江省教学研究项目（JG2013010268）

王佳伟（1982—），男，黑龙江哈尔滨，在读博士研究生，工程师，研究方向为控制系统实验与故障诊断技术．

E－mail：wangjiawei1982＠163．com