通用大断面水位面积计算方法存在瑕疵

刘彦章

(河北省石家庄水文水资源勘测局,河北 石家庄 052560)

通用大断面水位面积计算方法存在瑕疵

刘彦章

(河北省石家庄水文水资源勘测局,河北 石家庄 052560)

目前测站通用的大断面水位面积计算方法是通过先绘制断面图,再设定若干个分级水位，量取各分级水位对应的水面宽，将上、下分级水位水面宽平均值乘以对应的水位差，得到这两级分级水位之间的增量面积，逐级累积增量面积可得到大断面水位面积关系。这种方法必须将实测点高程逐点设为分级水位，否则，计算理论上存在瑕疵。实际中一般测站不会将每个高度的测点都考虑为分级水位,故开发利用Excel功能精确计算大断面水位面积关系。

大断面；分级水位；水位差；水面宽；面积；模板

1 传统方法及存在的瑕疵

1.1 传统计算方法

目前测站通用的大断面水位面积计算方法是通过绘制断面图,设定若干个分级水位，量取各个分级水位与各个河底高程实测点连线所包围的多个微小三角形或梯形断面对应的水面宽，并将其累加，以上、下分级水位累计的水面宽平均

值乘以对应的水位差，可得到这两级分级水位之间的增量面积，逐级计算可得到大断面水位面积关系[1-4]。其公式表达式为：

Fi+1=Fi+△F

(1)

式中：Fi+1为上级分级水位对应的大断面面积,m2;Fi为下级分级水位对应的大断面面积，m2;△F为两级分级水位对应的增量面积,m2。一般计算时采用列表方法进行计算[5]，见表1。

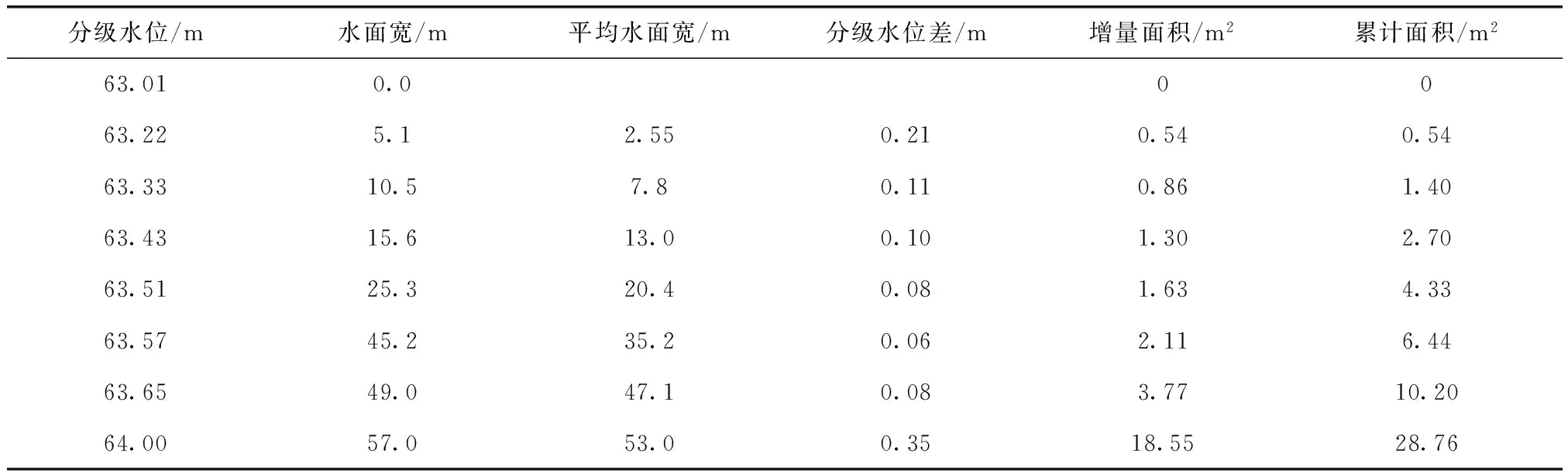
表1 水位面积计算通用表样

1.2 传统计算方法存在的瑕疵

(1) 由于是人工在图上量取长度，以及受绘图比例尺大小影响，量取的结果会因人而异，因此所求得的水位面积关系只是一种估算结果。这仅是这一方法存在不足的一个方面，其最大的问题还在于，如果不是将每个实测河底高程点设定为分级水位，并进行逐一量取水面宽度及计算，则这种方法在理论上存在重大缺陷。

此方法的理论基础依据是认为两个分级水位与各个河底高程实测点连线所包围形成的多个微小三角形或梯形断面必须是完整的，两个分级水位之间不能有实测河底高程点，也就是说，必须将每个河底高程点都设为水位分级高度，哪怕是两个实测河底高程点仅相差1 cm，并且，非河底高程点不能设定为分级水位，只有这样才能保证理论上没有计算误差。而实际情况绝非是这样的，一般测站不会把分级水位设的那么密，将每个高度的测点都考虑为分级水位，尤其是当两个或几个河底高程仅差几厘米时，只取其中之一列为分级水位。图1是某断面计算示意图，以此进行分析。

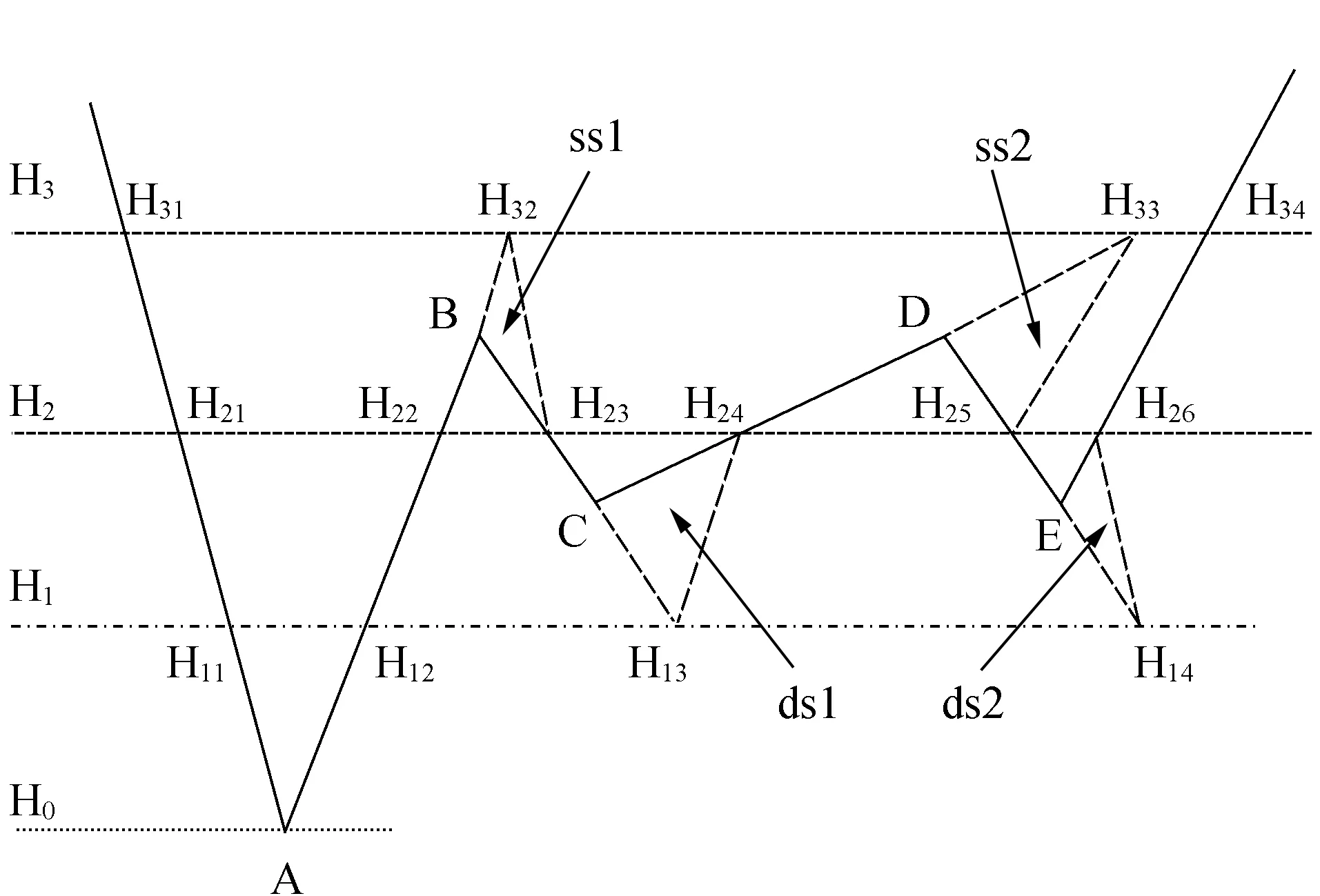
图1 断面计算示意图

(2)图1中A、B、C、D、E为河底测点，H0、H1、H2、H3为分级水位，H11、H12、及H21、H22、H23、H24、H25、H26和H31、H34为分级水位H1、H2、H3与断面曲线交叉点，H13、H14、H32、H33分别为H1、H3水位虚拟点。可以看出，H1、H2分级水位之间实际新增加的断面面积分别为H11—H21—H22—H12、H23—H24—C、H25—H26—E三部分；按传统方法计算分级水位增量面积(△F12)：上、下分级水位水面宽之和除以2乘以分级水位差。即：H11—H12、H21—H22、H23—H24、H25—H26分别对应的水面宽b0、b1、b2、b3之和除2乘以分级水位差h2-1，h2-1为H2—H1分级水位差。进行逐块拆分分析：第一块为H11—H12、H21—H22水面宽b0、b1相加除2乘以h2-1，第二块为H23—H24水面宽b2除2乘以h2-1，第三块为H25—H26水面宽b3除2乘以h2-1。可见，三块面积中仅第一块与实际相符，第二、三块分别比实际多算了，多算面积分别为ds1(C —H24—H13组成的面积)、ds2(E—H26—H14组成的面积)(ds—“多算”拼音简写)：

ds1=1/2*b2*(h2-1—h2-C)

(2)

ds2=1/2*b3*(h2-1—h2-E)

(3)

式中:h2-C、h2-E为H2分级水位与C点、E点高程之差,m。

(3)同样道理，可以分析在分级水位H2、H3时的计算增量面积。可以看出，H2、H3分级水位之间实际增加的面积为：H31—H21—H22—B—H23—H24—D—H25—H26—H34—H31组成的面积；而按传统方法计算增量面积(△F23)：H21—H22、H23—H24、H25—H26、H31—H34分别对应水面宽b1、b2、b3、b4之和除2乘以分级水位差h3-2，h3-2为H3—H2分级水位差，其中H31—H34水面宽可拆分为H31—H32、H32—H33、H33—H34三个水面宽。进行逐块拆分分析：第一块为H31—H32、H21—H22水面宽相加除2乘以h3-2，第二块为H32—H33、H23—H24水面宽相加除2乘以h3-2，第三块为H33—H34、H25—H26水面宽相加除2乘以h3-2。可见，三块面积中仅第一块与实际相同，第二、三块分别比实际少算了，少算面积分别为ss1(B —H32—H23组成的面积)、ss2(D—H33—H25组成的面积)(ss—“少算”拼音简写)：

ss1=1/2·(H23-H22)距离·(h3-2-hB-2)

(4)

ss2=1/2·(H25-H24)距离·(h3-2-hD-2)

(5)

式中：hB-2、hD-2分别为H3分级水位与B点、D点高程之差，m。

(4)误差分析。经过公式(1)累计后，多算与少算的面积会有所冲抵中和，但第一级和最后一级计算的面积会发生较大的误差，由于地形的千差万别这种抵消中和程度难以确定，也就决定着这种方法的具体误差不能确定，与实际断面形状有直接关系，对于某个断面可能不太大，可对于另一断面就可能产生较大误差。在图1中，如果B点上延至很接近H3，则少算面积ss1→0，与下面多算的面积ds1相抵消后会产生一个较大的正偏差。通过分析还发现，测点越接近分级水位，越可能产生较大的多算面积或少算面积。如果B、D点和C、E都各自延至H3、H1，则少算、多算面积ss1=0，ss2=0，ds1=0，ds2=0；也就是将所有河底高程实测点都设为分级水位时就没有计算误差。

(5) 当某一断面出现一个距离很长的平台的情况时，设定分级水位正好等于平台高程，就会出现这样一个问题，此处水面宽是按有水面宽对待还是按水面宽为0对待，以图1为例详加分析。在图1中，若C点位于H23处，D位于H25处，C、D之间是距离较远的一个平台地形，如果在计算H1—H2分级水位时，C—D之间水面宽按0考虑，则之间新增面积与实际相符；但在计算H2—H3分级水位时,由于水面宽上下平均相关联，H2—H3之间的平均水面宽会明显偏小，相应的新增面积会偏小，偏小值为1/2*(C—D)距离* (H3—H2)高差，也就是由于C—D距离按0计算，此处的面积不是实际的梯形面积，而是按三角形处理的。如果在计算H1—H2分级水位时C—D之间水面宽按D起点距减去C起点距考虑，则在计算H1—H2分级水位时会虚增不存在的一个三角形过水面积，虚增的值为1/2*(C—D)距离* (H2—H1)高差；由于水面宽上下平均相关联，而在计算H2—H3之间新增面积时此处新增面积与实际相符。因此，得到如下结论，仅受此项因素的影响，C—D之间水面宽按0考虑，最终面积值偏小；C—D之间水面宽按有数值考虑，最终面积值偏大。唯一正确的方法是分别采用两个水面宽，即这一分级水位有两个水面宽，0和平台长度，与此分级水位低的一级分级水位之间计算平均水面宽时此处水面宽按0计，与此分级水位高的一级分级水位之间计算平均水面宽时此处水面宽按平台长度计。

2 修正瑕疵

传统方法是按绘图比例量取折算水面宽，就存在一定误差，再加上方法理论上的缺陷，从而决定着所求得的水位面积关系是一种估算成果。这种方法的基本思路是将断面进行水平方向分割为若干三角形、梯形，逐级累计计算。

新的计算方法是对于某一水位下，以所有河底高程点为分割点做垂线交与分级水位线，进行纵向分割，可得到若干个三角形、梯形面积，分别将其计算并累加就会得到这一水位下精确的断面面积。

2.1 纵向分割计算原理

图2为某一断面纵向分割计算示意图，图中，H4为某一水位时的水面线，则这一水位对应的断面面积为点虚线和河底折线所组成的若干三角形、梯形面积之和。中间部分梯形面积可由分级水位、测点起点距、测点高程求得，两边的三角形面积则要先求得这一部分的水面宽，如图2中的XY。据几何相似形原理，有如下关系：

XY=ZW*AY/AW

(6)

式中：ZW为相邻两侧点Z、A水平间距，即A点起点距值-Z点起点距值，m；AY为测点A高程与H4水位之差，m;AW为测点A与测点Z高程差,m。这样三角形AXY面积为：

F=1/2*ZW*(AY)2/AW

(7)

用同样方法图中右边三角形面积也可计算出来。

图2 某一断面纵向分割计算示意图

2.2 编制Excel模板

基于上述原理，笔者编制了一套Excel模板，可以非常容易计算出给定的大断面水位面积关系，只需输入断面起点距、河底高程数据，其水位面积关系值及曲线自动显示出来。这种方法在理论上没有误差。

当然，上述H4水面线是比较简单的情况，实际上在低水部分，如图1中的H2水位，这一水面线位于一些测点之下，编写函数及公式时需要全面考虑各种情况从而计算各个单元面积。

模板编写方法是，将大断面测量成果输入或粘贴在A、B两列中，最多可输入100组数据，C列为自动形成的分级水位，L7放置其中一个分级水位，于是，在J10单元格编写第九行和第十行实测河底高程点之间水平间距公式：

IF($B11=0,0,IF($B10>$B11,IF($L$7<$B10,IF($L$7>$B11,($A11-$A10)*ABS($L$7-$B11)/ABS($B10-$B11),0),$A11-$A10),IF($L$7<$B11,IF($L$7>$B10,($A11-$A10)*ABS($L$7-$B10)/ABS($B10-$B11),0),$A11-$A10)))[6]

在I10单元格编写第九行和第十行分级水位差公式：IF($B10<=0,0,IF($L$7<$B10,0,$L$7-$B10))

以上两者相乘除2即为这一微小面积值，拖拽至最后一组实测点，求和可得到该分级水位下的大断面面积。对50个分级水位进行相应编写，可求得大断面水位面积关系。当然，大断面图和水位面积曲线图两者协调等内容还需应用大量Excel函数、功能进一步编写处理。

2.3 模板功能及使用方法简介

该模板自动设定分级水位。自动分为50个分级水位，可对低水部分、中水部分、高水部分，根据河底高程分布状态，指定三个低、中、高控制水位(将水位面积关系线分为3段)，各个控制水位下再设定分级水位层数，比如，把高程100m以下设为低水部分，低水以下设定10个分级水位，程序会自动将100减去河底高程最低点除以10，假定最低点高程为98m，则分级水位差为0.2m。如果分级水位差为多位小数，程序自动将其舍入为0.01m。低、中、高水位控制段的三者层数之和小于等于49(最低河底高程自动默认为一个分级水位，总分级最多50个)，程序已对其进行有效性控制，超范围则不予确认。

在模板中，只有起点距、河底高程这一区域的单元格(A8:B107)和水位分层、水位控制这6个单元格以及面积比例尺设定值，欲查看水位值这2个单元格能够选中并输入数值，其他单元格被锁定且不能选中。在模版中隐藏了大量公式及数据、工作表在后台工作。输入水位分层数量及相应控制水位后，水位面积关系数组以及曲线自动形成。改变分级水位层数，其相关数组及关系曲线上的关系点疏密状况也随之变化；改变控制水位，可以从关系线上看出低、中、高水位控制分界点(相同疏密程度分界点)位置随之改变。模板编写了使用说明，以方便用户参考。

该模板可以查看任意水位对应的面积。在G12单元格处输入水位，相应的面积就会随时显示。而且这一点以大红圆点突出的显示在关系曲线上，图3为模板界面截图。

图3 水位面积关系曲线Excel模板累面截图

3 结 论

如果用人工按上述纵向分割方法计算某一断面的水位面积关系，其计算工作量会相当大，正因如此，过去传统计算方法受计算工具条件限制才采用近似的方法计算水位面积关系。现在情况不同了，计算机的普及使精确计算绘制水位面积关系曲线变为可能且极其简单，采用模板不需要任何手工计算，只需将原始测量数据输入从别处复制粘贴在指定位置即可，进行一些设置，水位和面积数据以及曲线图自动生成。因此，应该采用简单、精确的方法，因此建议推广使用新方法。

[1] 王楠，时秀梅，单志学.利用EXCEL精确计算水位面积曲线的方法[J].2013(z1)：210-211.

[2] 中华人民共和国水利部.SL 58-2014水文测量规范[S].北京：中国水利水电出版社，2014.

[3] 水利电力部水利司.水文测验手册[M].北京：水利电力出版社，1975.

[4] 王春泽.水文知识读本[M].北京：中国水利水电出版社，2011.

[5] 中华人民共和国水利部.SL 247-2012水文资料整编规范[S].北京:中国水利水电出版社,2013.

[6] Excel研究组.Excel 2007函数与公式速查手册[M].北京：电子工业出版社，2008.

刘彦章(1961-)，男，高级工程师，从事水文基础测验工作。E-mail：969583772@qq.com

P332

A

2096-0506(2015)06-0050-04