基于相关度的蚁群优化算法对内热源位置的识别
李博汉, 卢 玫
(上海理工大学能源与动力工程学院,上海 200093)
基于相关度的蚁群优化算法对内热源位置的识别
李博汉, 卢 玫
(上海理工大学能源与动力工程学院,上海 200093)
为了提高寻源导热反问题的求解精度和求解速度,针对导热问题中热源位置对边界温度分布影响的特点,提出了适用于寻源导热反问题的基于相关度的蚁群优化算法.该方法分别针对热源位置的每一个坐标,运用能反映计算测点温度曲线与真实测点温度曲线相似程度的量即相关度的方法来构造其相对应的启发信息值;并对蚁群优化算法中路径选择机制、目标函数的构造进行了改进.以数值计算代替实际试验得到测点温度,并对反问题进行计算机编程试验.计算结果表明,此种启发信息值的标定方法和目标函数的构建方法能够很好地区分出路径的质量,从而提高了蚁群收敛到最好路径的速度.计算效率较不考虑相关度的蚁群算法提高了18%~60%.
蚁群优化;寻源导热反问题;路径构造;目标函数
Key words:ant colony optimization;inverse heat source problem;path construction;objective function
工程上的热力设备设计、金属无损探伤,医学上的肿瘤诊断和治疗等问题都能抽象为对有内热源物体热源位置识别的问题,即寻源导热反问题[1].运用导热反问题的领域十分广泛,例如,金属的切割与焊接、新材料的开发与应用、瞬态热量计的研制、精密温度测量等.由于该问题有非线性或不适定性的特点,求解较为困难.又因其具有广泛的应用背景,长期以来吸引着大量学者对其不断地进行探索研究.求解此类问题的方法主要分为两大类:一类是基于概率的求解方法(stochastic ones),另一类是基于梯度的求解方法(gradient-based ones)[2].具体的解决方法有共轭梯度法、快速下降法以及近年来较多采用的仿生优化算法,如遗传算法、神经网络法、粒子群算法等.Geng等[3]采用变分迭代算法来求解寻源导热反问题.Xiong等[4]则采用了提克洛夫规则化对无限大边界物体中的热源进行识别.近年来,随着一些仿生优化算法的出现和成熟,运用这些方法来优化求解导热反问题也是十分普遍的.例如,Liu[5]运用遗传算法来寻找平面热源.Deng等[6]则运用神经网络算法来确定未知的边界条件.张涛等[7]采用粒子群优化算法对寻源导热反问题进行了求解.
1992年意大利学者Dorigo等[8]提出了一种新的仿生优化算法——蚁群优化算法(ACO).此算法在求解复杂优化问题时具有很大的优势,已成为国内外学者研究的热点.而针对蚁群算法的应用对象,近年来主要集中在旅行商问题、顺序排序问题、广义分配问题、多重背包问题、网络路由问题及动态旅行商问题等.
对于寻源导热反问题而言,其计算求解过程中包含有对导热正问题的数值求解计算.数值计算的特点是对计算域划分网格.而对热源的处理是将其布置在其中的一个网格当中,即热源可能的位置选取是离散在这些网格中的.显然这是一个典型的离散问题,而蚁群优化算法的一大特点就是解决离散优化问题[9].Hetmaniok等[10]比较系统地研究了蚁群优化算法,并运用此算法来确定导热系数.黄少君等[11]则改进了蚁群算法,并引入了优化排序机制,提高了算法的收敛速度.
蚁群优化算法有两大特点:一是蚂蚁的行为主要取决于路径上的信息素浓度与启发式信息值,而启发式信息值的大小直接与路径的长短有关[12].路径越短,启发式信息越大,蚂蚁选择此路径的概率就越大.蚁群算法正是利用这种信息的正反馈机制,在一定程度上提高了算法的求解性能,但同时也使得算法容易陷入局部最优.二是其目标函数不只是确定最终结果的正确性,其值还用于路径上信息素的积累.而信息素的累计值直接影响到蚂蚁的行为[13].所以,基于以上两个特点,本文试图从路径构造、启发信息值的选取和目标函数的构造入手,找到一种合理的适用于寻源导热问题的路径构造方法和目标函数的形式,从而加快蚂蚁的搜索速度和提高算法的求解精度,并避免局部最优的发生.
1 寻源导热反问题数学模型
1.1 物理模型
选取计算域为0.1 m×0.1 m的带有内热源的二维稳态导热问题为算例来验证蚁群优化算法中路径构造方法和目标函数选取的有效性,如图1所示,具体物理参数如表1所示.计算域被划分成100× 100的结构化网格.点热源布置在(0.040 5, 0.030 5)位置的一个网格内,测点布置在y=0和x=0.1边界上,测点布置如图1中边界上的点所示,测点的具体位置如表2和表3所示.通过对正问题的计算代替物理试验,得到布置在边界上的测点温度值,再将测点温度代入反问题中进行计算,验证是否能够找到点热源的位置.通过反问题中正问题的计算次数来比较此种路径构造方法和目标函数的选取方法是否能够提高计算效率和计算精度.

图1 二维导热问题物理模型Fig.1 Physical model of the 2 D heat conduction problem

表1 基本参数Tab.1 Fundamental coefficients

表2 y=0边界测点位置及其真实温度(由数值计算得到)Tab.2 Measurement point position and its temperature at the boundary of y=0
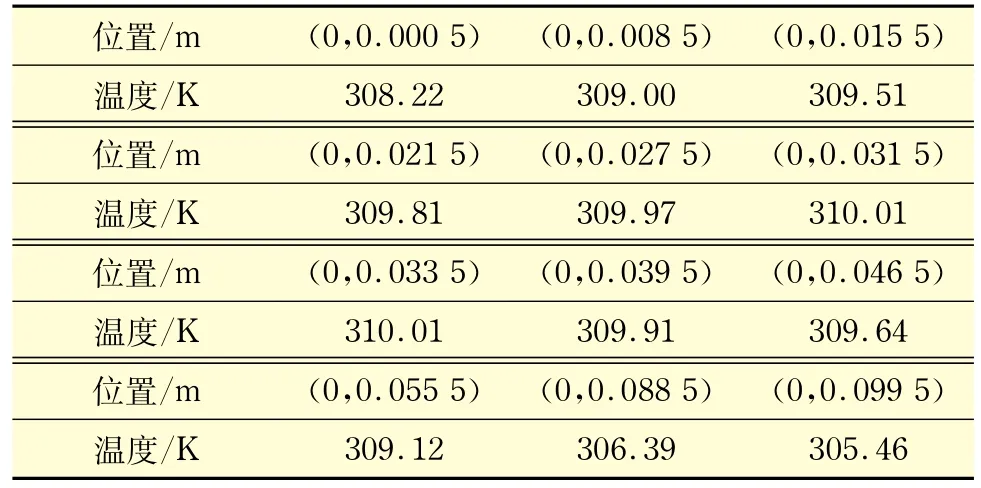
表3 x=0.1边界测点位置及其真实温度(由数值计算而得)Tab.3 Measurement point position and its temperature at the boundary of x=0.1
1.2 数学模型
描述上述二维稳态导热问题的微分方程为

式中,λ为导热系数;T为温度;S为源项.边界条件为

2 基于寻源导热反问题的蚁群优化算法改进
由于热源的可能位置是离散地分布在所划分的某个网格当中的,最简单的方法就是将热源一次置于这些网格当中,计算测点的温度值,再与真实测点温度值进行比较,从而确定热源的真实位置.但是,由于网格划分众多,且每次数值计算花费的时间相当长,依次将热源带入所有可能的位置进行计算将变得不切实际.所以,要应用优化算法对问题进行优化计算求解.由于蚁群优化算法适用于离散问题,所以,本文选取蚁群优化算法,并针对导热问题自身特点对其改进,进行优化求解.
2.1 路径的构造方式
蚁群算法通常用于实际的路径搜索问题,例如,旅行商问题(TSP),其路径就是指真实的路径.而对寻源导热反问题而言,其路径的定义就变得十分抽象.
由于计算域被划分成100×100的网格,而点热源的位置又分布在其中某个网格的中央,所以,在反问题的计算中点热源的位置选取有100×100种可能性,即蚂蚁必须在x轴上的100个可能的坐标中选取热源的xi(i=0,1,…,99)坐标,同样,在y轴上的100个可能坐标中选取热源的yj(j=0,1,…, 99)坐标,从而确定点热源的位置.本文称某一坐标轴上可能选取的坐标值为一条路径.就本例而言,在x轴上有100条路径,在y轴上也有100条路径.每一条x轴上的路径和y轴上的路径构成了蚂蚁找到热源的完整的路径.
2.2 启发信息值的改进
对于导热反问题而言,能够找到一个能够准确反映路径质量的评定标准十分重要,即要找到某种计算方法能够准确而有效地标定每条路径上的启发式信息值,从而引导蚂蚁快速准确地找到最佳路径.就蚁群算法解决的传统问题(如TSP问题[13])而言,其路径的长度是一个已知量.通常将路径长度的倒数值作为此路径的启发信息值,蚂蚁会通过这一启发值依照概率来选择路径.很显然,较短的路径对应着较大的启发值,即被蚂蚁选中的概率较大.但就导热问题而言,路经的质量并不是事先知道的,即蚂蚁必须先随机地选择一条完整的路径,得到一个点热源的坐标值(xi,yj),再代入正问题中进行计算,将计算得到的测点温度值与真实的测点温度值进行比较后才能确定路径的质量.这使得寻找到一种合适的路径启发信息值的标定方法变得尤为重要.
通常的处理方法是用计算测点温度与真实测点温度的差平方和的倒数1∑(Tt-Tr)2作为路径启发信息值来反映路径质量.其中,Tt和Tr分别为计算得出的测点温度与测点的真实温度.如果在某次随机选择中选择到的热源位置十分接近真实的热源位置,此时计算出来的测点温度值与真实值将会相差很小,则其差平方和的倒数值会很大,这的确能从某种程度上反映出路径质量的好坏,但这种方法存在着一个很大的问题,就是xi路径与yj路径是相互影响的,即在选择相同的xi路径后,路径y的变化会影响边界温度的变化,从而导致1∑(Tt-Tr)2的值发生很大变化.如果再以此值作为xi路径的启发信息值,就会造成标定在某一路径上的启发信息值的不确定性和不真实性.这种影响从图2能够清楚地看出.图2所示曲线中实线为点热源布置在真实位置(0.040 5,0.030 5)处计算得到的x=0.1边界上的温度分布曲线,其它3条曲线则是保持点热源的y坐标值不变,仅改变x坐标值的情况下计算得出的x=0.1边界上的温度分布曲线.从图2中的曲线可以看到,如果采用1∑(Tt-Tr)2来标定路径的质量,那么,当只改变x坐标时,计算出的温度曲线与真实温度曲线的间距相差很大,如果用此值来标定真实热源所在路径y=0.030 5上的启发信息值就势必会造成此条路径被选中的概率减小,从而不利于蚂蚁找到真实的热源位置.
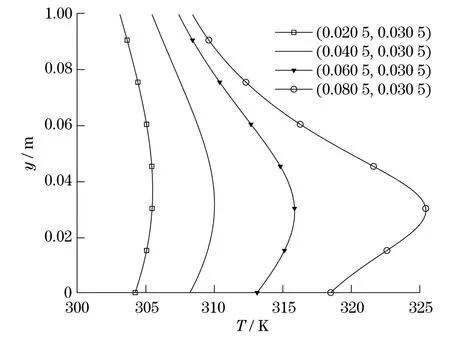
图2 y坐标不变只更换x坐标所计算出的x=0.1边界温度分布曲线Fig.2 Temperature profiles at the boundary of x=0.1 with different point source positions
基于以上的原因,必须找到一个相互影响较小、并且能区分出路径质量好坏的启发信息值计算方法来标定路径的质量,让蚂蚁更好地识别出路径的质量,从而更快地找到最优路径.
本文采用了能够反映计算测点温度值与真实测点温度值走势的相似程度即相关度的方法来构造路径的启发信息值,其计算式为
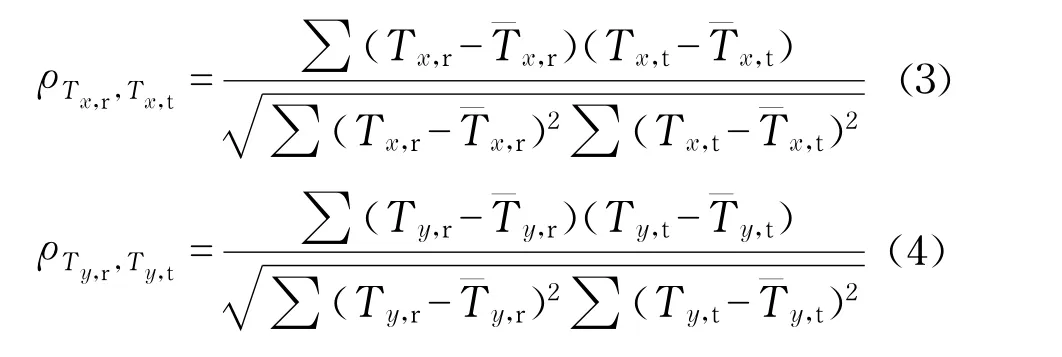
式中,ρ为真实测点温度与计算测点温度的相关度.下标r表明此温度为真实的测点温度,下标t代表此温度值是蚂蚁随机地选择了某个热源位置后代入正问题中计算得来的测点温度值.下标x与y分别表示此温度值是与x轴平行的边界上测点的温度值和与y轴平行的边界上测点的温度值.就本例而言, Tx,r,Tx,t分别表示y=0边界测点的真实温度值和计算温度值;Ty,r,Ty,t分别表示x=0.1边界测点的真实温度值和计算温度值.
式(3)和式(4)分别计算了与两坐标轴平行的两边界上的计算测点温度与真实测点温度的相关性,即温度分布曲线的相似程度,ρ∈[-1,1].如果ρ的值越接近1,说明两条曲线的相似程度越高,那么,表明该路径越好.
采用相关度的好处可以从图2观察到,虽然这两条温度分布曲线与真实温度分布曲线温度值相差很大,它们却是十分的相似,即走势一致.这说明当某条路径不变,只改变另一条路径时,所得到的温度曲线都是相似的.所以,如果能用反映计算测点温度曲线与真实测点温度曲线走势相似程度的相关度的方法来计算路径的启发值,就可以减小另一坐标的变化而造成的影响.

但是,即便采用了相关性原理来构造路径,也不能完全消除另一坐标的影响.为此,本文在采用相关度的同时计算了其加权平均值,来反映该路径的启发式信息值,从而进一步减小路径两坐标的影响,保证了路径启发信息值的稳定性.路径启发信息值ηp的计算方法如式(5)所示.

式中,p为一条路径,在本文中为热源的某一坐标xi或者yj;kp为p路径被蚂蚁选择的次数.
基于以上原因,选择温度测点时必须遵守两点:一是选择测点时,应尽量使测点的温度能够真实地反映此边界的温度曲线的走势,这一点是十分重要的,利用红外热像仪检测就能轻松解决此问题;二是对于二维问题,对应于笛卡尔坐标系,必须在物体的左边界或右边界以及物体的上边界或下边界分别布置测点温度,只有这样才能够分别计算出x轴各条路径和y轴各条路径的相关度.但是,由于在实际工程应用中往往受到周围环境的限制,有时无法分别测量两个边上的温度,因此,针对只能测量一个边界上的温度的情况,本文也给出了计算路径启发信息值的方法.
从图2可以看到,当热源的y坐标不变,x坐标发生变化时,计算温度曲线与真实温度曲线的接近程度恰能反映热源的x坐标与真实热源x坐标的接近程度.如果y=0边界上无法布置测点而只能在x=0.1边界上布置测点,那么,在y=0边界上的路径启发信息值

式中,kxi表示路径xi被蚂蚁选择的次数;ny表示在平行于y轴边界上的测点数目,本文中ny表示y=0边界上的测点数目.
同理,当x=0.1边界无法布置测点时,计算x=0.1边界的路径启发信息值

式中,kyj表示路径yj被蚂蚁选择的次数;nx表示在平行于x轴边界上的测点数目,本文中nx表示x=1边界上的测点数目.
式(6)和式(7)的分子反映了计算测点温度与真实测点温度的接近程度.由图2可以看到,如果x的位置越接近真实的温度曲线,那么,计算温度就会越接近真实温度,因此,式(6)和式(7)能够反映出无测点温度边界上路径的质量.
2.3 目标函数的改进
由于在蚁群优化算法中蚂蚁是根据目标函数的计算值来更新路径上的信息素的,所以,一个有指向性的目标函数不仅能够保证计算的准确性,还能使路径上的信息素值具有更强的导向性,指引蚂蚁快速找到最优路径.本文中目标函数的计算值公式引入了相关度ρ.目标函数

式中,n为测点的总数目.
当只有一个边界上有测点时,目标函数

这种目标函数的构造方法不仅考虑了计算测点温度曲线与真实测点温度曲线的接近程度,而且更能反映其相似程度,从而能够更好地指示路径的质量,加快蚂蚁收敛到最好路径的速度.
2.4 变概率的伪随机比率路径选择机制
根据寻源导热反问题的特点,如果蚂蚁选择了一条较好的路径,那么,在这条好的路径周围可能会存在更好的路径,即离热源位置越近,路径质量就越好.根据此特点,本文提出了变概率的伪随机比率路径选择机制,即蚂蚁选择当前最优路径的概率q0是随搜索过程的进行程度而变化的.具体路径选择机制如式(10)~(12)所示.
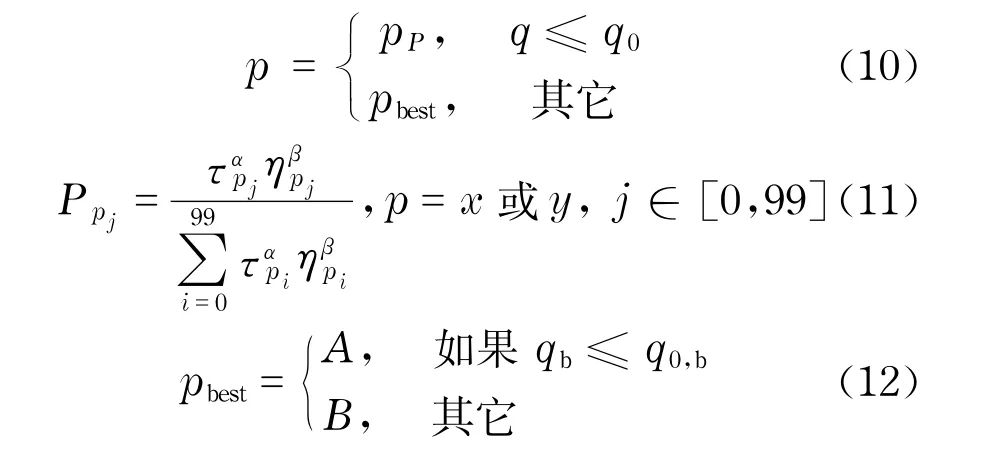
式中,p为路径;pP表示依据式(11)按照概率选择出来的路径;pbest为目前最好的路径或其周围的路径;A为目前最好的路径;B为目前最好路径周围的路径;q0为目前蚁群进行路径选择的次数占总选择次数的百分率;q为0~1的随机数;Ppj为pj路径被选中的概率;τ为路径上信息素浓度;α和β为能见度指数,决定路径上启发式信息值与信息素浓度的相对重要性,本文中α和β均取1,说明路径启发信息值与信息素浓度同等重要;q0,b为目前蚁群进行路径选择的次数占总选择次数的百分率,且q0,b的最大值不超过0.6;qb为0~1的随机数.
式(10)—(12)的路径选择规则有两种:一种是根据路径上信息素浓度和路径的启发信息值依照概率来选择,如式(11)所示;另一种是直接选择目前最好的路径或者目前最好路径周围的几条路径,如式(12)所示.式(10)则控制两种选择方式使用的概率.本文中蚂蚁共进行1 500次路径搜索过程.在路径搜索过程的前期,蚂蚁进行路径搜索的次数还不是很多,所以,q0的值比较小,根据式(10),蚂蚁选择基于概率的选择方式(式(11))的几率比较大,这样能增大蚂蚁探索新路径的可能性,避免局部最优的发生;而随着路径搜索过程的进行,q0的值逐渐增大,蚂蚁选择第二种搜索方式(式(12))的概率增大.这样能使蚂蚁在搜索过程的后期快速地收敛到最好路径上,提高计算效率.根据多次计算,本文中设置q0的最大值为0.8,这表明在搜索过程后期依然能保证20%的概率让蚂蚁使用基于概率的搜索方式,从而进一步防止局部最优的发生.式(12)中q0,b的作用与式(9)中q0的作用相似,即当选择了式(12)的选择方式后,在前期使蚂蚁尽量选择目前最好路径周围的路径,以提高蚂蚁探索新路径的可能性,防止局部最优的发生;而在后期则提高蚁群的收敛速度和计算效率.根据大量计算得出q0,b的最大值取0.6为佳.
2.5 基于相关度的局部信息素更新策略
在每一只蚂蚁完成路径搜索之后都要进行局部信息素更新,其更新方式为
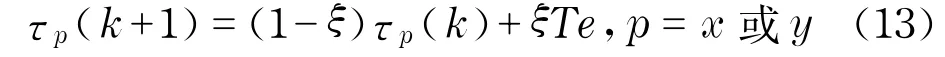
式中,τ为信息素浓度;下标p为某条路径;ξ为信息素的局部挥发系数,0<ξ<1;k为蚂蚁选择的次数.
本文中的局部信息素更新式与文献[11-12]的有所不同.在本文中直接选用目标函数的值来进行局部信息素的更新.由于目标函数中包含了相关度的概念,使得在信息素更新时能够更好地综合考虑两条路径的质量优劣,进一步增强了路径之间的区分度.当配合适当大小的信息素初始值后,此更新式不仅能够减小低质量路径上的信息素浓度,使得这些路径不容易被蚂蚁找到,而且还能增加高质量路径上的信息素浓度,从而提高此路径被蚂蚁选中的概率,使得蚁群更容易收敛到最优路径上.此种更新方法既能提高蚂蚁的收敛速度,又能有效避免局部最优的发生.大量计算表明,路径信息素的初始值设置在400~500之间为宜.
2.6 全局信息素更新策略
当蚁群中所有蚂蚁都完成一遍搜索之后,在目前最好的路径上将进行信息素的全局更新.更新方式为

本文并没有使用目标函数的值来进行信息素的全局更新,而是采用所有测点的计算测点温度与真实测点温度的差平方和的倒数值来进行信息素更新,因为这能够反映蚂蚁找到的最终结果的质量,有利于在算法后期避免局部最优的发生.
3 算法基本流程
上述改进算法的计算流程如图3所示.计算中蚁群总共有100只蚂蚁,蚁群共进行15次循环搜索,即总共进行1 500次的路径搜索,并把最终的最优路径作为计算结果.经过计算,1 500次路径搜索已经足够多,蚂蚁基本会在第600次左右的搜索后集中于同一路径上.
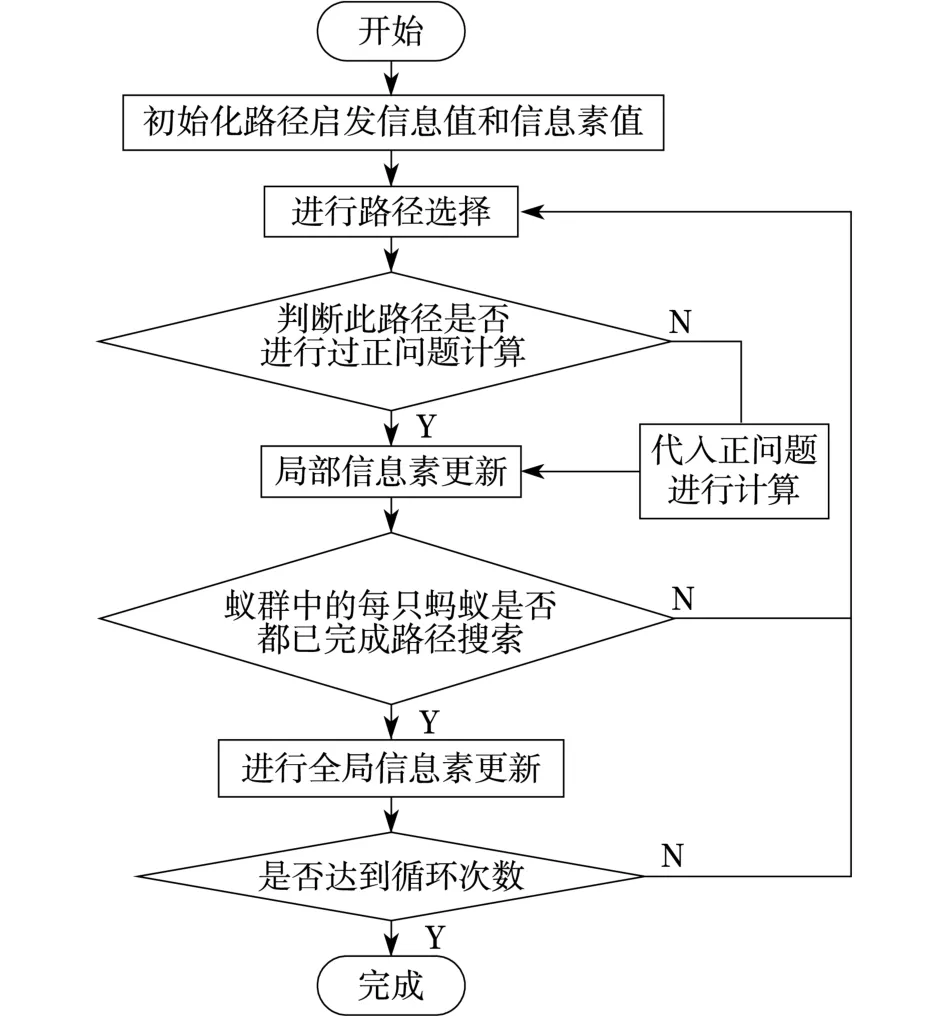
图3 算法流程图Fig.3 Flow chart
4 计算验证
针对以上所提出的路径启发信息值的标定方法、目标函数的构建方法、路径选择机制以及信息素更新机制,运用C语言进行计算机编程计算.在计算结果优劣的判定方面,由于程序的编译及运行环境不同,所以,并不将程序运行时间作为判定标准,而是选取每次反问题计算过程中正问题的计算次数为判断标准.在一次反问题计算过程中,收敛性好的算法对应着相对较少的正问题计算次数.由于蚁群优化算法是一种基于概率的求解方法,所以,一次反问题的计算结果(反问题中正问题的计算次数)并不能说明问题.所以,本文分别针对在y=0和x=0. 1边界上布置测点、只在x=0.1边界上布置测点以及只在y=0边界上布置测点这3种情况进行了200次的反问题计算,并将200次计算的平均结果与文献[11]的计算结果进行对比.y=0边界以及x =0.1边界测点位置与对应的测点温度分别如表2和表3所示.
图4给出了在x=0.1以及y=0边界上均布置测点时的计算结果.横坐标a为每一次的反问题试验计算.纵坐标d表示每次反问题计算中正问题的计算次数.曲线c表示目前为止正问题计算的平均次数.从图4中可以看到,当进行多次反问题的计算后,平均每次反问题中所计算的正问题的次数会稳定在60次.
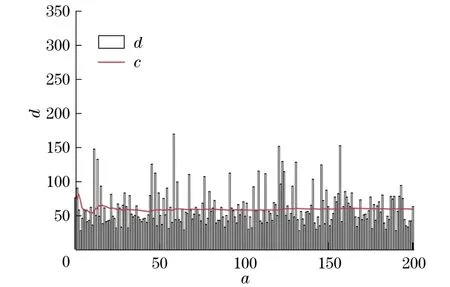
图4 测点布置在x=0.1以及y=0边界的计算结果Fig.4 Computational results when placing the measurement points at the boundary of x=0.1 and y=0
图5与图6分别为测点只布置在y=0边界或者x=0.1边界上时的计算结果.每次反问题中正问题的计算次数分别稳定在137次和135次.计算结果显然要次于两边界均布置测点的情况.这是由于少了一个边界上的测点温度,无法通过相关度的方法来标定此边界路径启发信息值,从而影响到蚂蚁对路径质量的识别,不利于蚁群收敛到最佳路径上来.
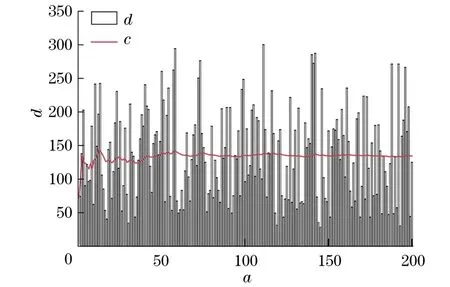
图5 测点布置在y=0边界的计算结果Fig.5 Computational results when placing the measurement points at the boundary of y=0

图6 测点布置在x=0.1边界的计算结果Fig.6 Computational results when placing the measurement points at the boundary of x=0.1
表4将采用本文方法的计算结果与文献[11]的结果进行了对比,可见在两边界均布置测点的情况下,本文所述改进方法能将计算效率提高60%左右;而对于只有一个边界布置测点的情况,本文的方法也能将计算效率提高将近20%.由此可见,采用以相关度的方法来标定路径启发信息值并以此来构建目标函数的确能够有效地减少计算量,提高计算效率和计算精度.

表4 计算结果汇总Tab.4 Summary of computational results
5 结 论
针对导热问题的特点改进了蚁群优化算法,使其适用于寻源导热反问题.建立了以计算测点温度与真实测点温度的相关度值作为路径启发信息值的标定方法,引入了相关度的概念构造目标函数,采用了伪随机比率路径选择机制和基于相关度的局部信息素更新策略.通过计算机编程计算,验证了改进蚁群算法的有效性.计算结果表明,在两边均布置测点的情况下采用相关度的蚁群优化算法较没有采用相关度的蚁群优化算法的计算效率提高了60%左右;在只有一边布置测点的情况下,计算效率也有将近20%的提升.说明采用相关度的蚁群优化算法在寻源导热反问题的计算中能够明显加快蚂蚁算法的收敛速度,从而提高了计算效率和计算精度.
[1] Su J,Neto A J S.Two-dimensional inverse heat conduction problem of source strength estimation in cylindrical rods[J].Applied Mathematical Modelling, 2001,25(10):861-872.
[2] Liu F B.A hybrid method for the inverse heat transfer of estimating fluid thermal conductivity and heat capacity [J].International Journal of Thermal Sciences,2011, 50(5):718-724.
[3] Geng F Z,Lin Y Z.Application of the variational iteration method to inverse heat source problems[J]. Computers&Mathematics with Applications,2009,58 (11/12):2098-2102.
[4] Xiong X T,Wang J X.A Tikhonov-type method for solving a multidimensional inverse heat source problem in an unbounded domain[J].Journal of Computational and Applied Mathematics,2012,236 (7):1766-1774.
[5] Liu F B.A modified genetic algorithm for solving the inverse heat transfer problem of estimating plan heat source[J].International Journal of Heat and Mass Transfer,2008,51(15/16):3745-3752.
[6] Deng S,Hwang Y.Applying neural networks to the solution of forward and inverse heat conduction problems[J].International Journal of Heat and Mass Transfer,2006,49(25/26):4732-4750.
[7] 张涛,卢玫,陶亮,等.基于粒子群优化算法的寻源导热反问题研究[J].上海理工大学学报,2013,35(4): 377-381.
[8] Dorigo M,Maniezzo V,Colonri A.The ant system: optimization by a colony of cooperating agents[J]. IEEE Transactions on Systems,Man and Cybernetics, Part B,1996,26(1):1-13.
[9] Dorigo M,Caro G D,Gambardella L M.Ant algorithms for discrete optimization[J].Artificial Life,1999,5 (2):137-172.
[10] Hetmaniok E,Slota D,Zielonka A.Application of the ant colony optimization algorithm for reconstruction of the thermal conductivity coefficient[M]∥Swarm and Evolutionary Computation.Berlin:Springer,2012.
[11] 黄少君,卢玫,张涛,等.适用于寻源导热反问题的改进蚁群系统[J].工程热物理学报,2013,34(4): 694-697.
[12] Dorigo M,Gambardella L M.Ant colonies for the traveling salesman problem[J].BioSystems,1997,43 (2):73-81.
[13] Dorigo M,Stutzle T.Ant colony optimization[M]. London:The MIT Press,2004.
(编辑:石 瑛)
Identification of Internal Heat Source Position by Using Coalition-Based Ant Colony Optimization Algorithm
LIBohan, LUMei
(School of Energy and Power Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)
In order to improve the accuracy and efficiency in solving the inverse heat source problem,a coalition-based ant colony optimization method was introduced based on the features of the influence of heat source position on boundary temperature profiles.In the method,the coalition coefficient that reflects the similarity between the real temperature profile and the measured ones was selected as the heuristic information value for each coordinate of the position of heat source. The route construction rule and the building of objective in the ant colony optimization were also modified.Instead of the actual experiments,the temperature measurements at the measurement points were obtained from numerical simulations.With the help of computer programming,several times of computation were carried out to test the modified algorithm.The results show that the definition of the heuristic information value and the method of building objective functions can help the ants to identify the quality of the path,so that the ants can converge on the real route quickly. The computational efficiency is improved by 18%~60%compared with that of the algorithm that does not consider the coalition coefficient.
TK 124
A
1007-6735(2015)03-0225-08
10.13255/j.cnki.jusst.2015.03.005
2014-01-05
国家自然科学基金资助项目(51176126)
李博汉(1987-),男,硕士研究生.研究方向:导热反问题.E-mail:523215842@qq.com
卢 玫(1957-),女,教授.研究方向:强化传热和能量有效利用.E-mail:rose_luu@usst.edu.cn

