游泳运动员选拔问题的求解

隋 英 畅春玲 韩孺眉

(沈阳建筑大学 理学院 辽宁 沈阳：110168)

游泳运动员选拔问题的求解

隋 英 畅春玲 韩孺眉

(沈阳建筑大学 理学院 辽宁 沈阳：110168)

游泳运动员的选拔是一个值得研究的典型指派问题，将该问题转化成一般的线性规划问题，然后采用数学计算软件Mathemaica进行求解，获得良好的效果。

指派问题；线性规划；数学软件

游泳运动员的选拔是一个值得研究的典型指派问题，即：整数规划问题中的0-1规划问题。该问题可以通过常用的数学软件Mathemaica、Matlab、Lindo、Lingo等进行求解。本文尝试用Mathemaica进行求解。

1 问题的提出

某班准备从5名游泳队员中选择4人组成接力队，参加学校的4×100米混合泳接力赛。5名队员4种泳姿的百米平均成绩如表1所示，问应如何选拔队员组成接力队？

表1 队员4种泳姿的百米平均成绩(单位：秒)

2 问题分析

问题是要从5名队员中选出4人组成接力队，每人一种泳姿，并且4人的泳姿各不相同，使接力队的成绩最好。容易想到的一个办法是穷举法，组成接力队的方案共有5﹗=120种，逐一计算后做比较，即可找出最优方案。显然这样做的计算量很大，不是解决这类问题的最好办法，尤其是随着问题规模的变大，穷举法的计算量将是无法接受的。于是，我们考虑用0-1变量来表示一个队员是否入选接力队，从而建立该问题的0-1规划模型。

3 模型建立及求解

记甲、乙、丙、丁、戊分别为队员i=1,2,3,4,5；记蝶泳、仰泳、蛙泳、自由泳分别为泳姿j=1,2,3,4。记队员i的第j种泳姿的百米平均成绩为cij(单位：秒)。

决策变量：引入0-1变量xij，若选择队员i参加第j种泳姿的比赛，记xij=1，否则记xij=0。

约束条件：根据组成接力队的要求，xij应该满足下面两个约束条件：

(1)每人最多只能入选1种泳姿，即：

综上可得该问题的整数规划模型：

利用Mathematica 8求解模型

In[1]:=Minimize [ {66.8x11+ 75.6x12 +87x13+58.6x14+ 57.2x21+66x22+66.4x23+53x24+78x31+67.8x32+84.6x33+59.4x34+70x41+74.2x42+69.6x43+57.2x44+67.4x51+71x52+83.8x53+62.4x54

x11+x12+x13+x14 <= 1,

x21+x22+x23+x24<= 1,

x31+x32+x33+x34<= 1,

x41+x42+x43+x44<= 1,

x51+x52+x53+x54<= 1,

x11+x21+x31+x41+x51==1,

x12+x22+x32+x42+x52==1,

x13+x23+x33+x43+x53==1,

x14+x24+x34+x44+x54==1,

x11==1‖x11==0,x12==1‖x12==0,

x13==1‖x13==0,x14==1‖x14==0,

x21==1‖x21==0,x22==1‖x22==0,

x23==1‖x23==0,x24==1‖x24==0,

x31==1‖x31==0,x32==1‖x32==0,

x33==1‖x33==0,x34==1‖x34==0,

x41==1‖x41==0,x42==1‖x42==0,

x43==1‖x43==0,x44==1‖x44==0,

x51==1‖x51==0,x52==1‖x52==0,

x53==1‖x53==0,x54==1‖x54==0},

{x11,x12,x13,x14,x21,x22,x23,x24,x31,x32,x33,x34,x41,x42,x43,x44,x51,x52,x53,x54} ]

Out[1]=No more memory available.

Mathematica kernel has shut down.

Try quitting other applications and then retry.

即：按照0-1规划的命令来做这个问题，没有找到答案。于是将该问题转化成一般的线性规划问题来求解。

该问题的决策变量和目标函数保持不变，约束条件进行适当的调整，把0-1规划问题转化为一般的线性规划问题来求解

约束条件：根据组成接力队的要求，xij应该满足下面三个约束条件：

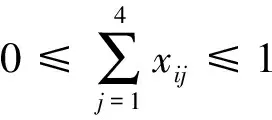
(2)每种泳姿必须有1人且只能有1人参赛

(3)非负性要求：xij≥0 ，i=1,2,3,4,5，j=1,2,3,4。

综上可得该问题的线性规划模型：

利用Mathematica求解模型

In[1]:=Minimize [ {66.8x11+ 75.6x12 + 87x13+58.6x14+ 57.2x21+66x22+66.4x23+53x24+78x31+67.8x32+84.6x33+59.4x34+70x41+74.2x42+69.6x43+57.2x44+67.4x51+71x52+83.8x53+62.4x54

x11+x12+x13+x14 <= 1,

x21+x22+x23+x24<= 1,

x31+x32+x33+x34<= 1,

x41+x42+x43+x44<= 1,

x51+x52+x53+x54<= 1,

x11+x12+x13+x14 >= 0,

x21+x22+x23+x24>= 0,

x31+x32+x33+x34>= 0,

x41+x42+x43+x44>= 0,

x51+x52+x53+x54>= 0,

x11+x21+x31+x41+x51= =1,

x12+x22+x32+x42+x52= =1,

x13+x23+x33+x43+x53= =1,

x14+x24+x34+x44+x54= =1,

x11>= 0,x12>= 0,x13>= 0,x14>= 0,

x21>= 0,x22>= 0,x23>= 0,x24>= 0,

x31>= 0,x32>= 0,x33>= 0,x34>= 0,

x41>= 0,x42>= 0,x43>= 0,x44>= 0,

x51>= 0,x52>= 0,x53>= 0,x54>= 0},

{x11,x12,x13,x14,x21,x22,x23,x24,x31,x32,x33,x34,x41,x42,x43,x44,x51,x52,x53,x54} ]

Out[1]={253.2,{x11->0.,x12->0.,x13->0.,x14->1.,x21->1.,x22->0.,x23->0.,x24->0.,x31->0.,x32->1.,x33->0.,x34->0.,x41->0.,x42->0.,x43->1.,x44->0.,x51->0.,x52->0.,x53->0.,x54->0.}}

4 结论

本文尝试用数学计算软件Mathemaica进行求解游泳运动员选拔问题，但在求解的过程中发现，使用Mathemaica求解简单的0-1规划问题尚可，但当决策变量的个数增加后，Mathemaica求解0-1规划问题问题就变得困难了，这是因为多个决策变量的0-1规划问题可能会导致一个冗长的分支定界计算。当分支定界计算时间很长仍得不到最优解时，适当地对输入模型进行一些等价变换，可能对问题的求解会有所帮助。因此，本文将游泳运动员的选拔问题由整数规划的0-1规划问题转化成一般的线性规划问题，然后通过Mathemaica软件进行求解，从而得出了问题的最佳求解方案。

[1] 姜启源，谢金星，叶俊.数学模型(第3版)[M].北京：高等教育出版社，2003．

[2] 谢金星，薛毅.优化模型与LINDO/LINGO软件[M]．北京：清华大学出版社，2005．

[3] 万中，曾金平.数学实验[M]．北京：科学出版社，2002．

[4] 李汉龙，缪淑贤，韩婷．Mathematica基础及其在数学建模中的应用[M]．北京：国防工业出版社，2013．

(责任编辑：李文英)

Seeking Solutions to Selection of Swimming Athletes

SUI Ying CHANG Chunling HAN Rumei

(Science School of Shenyang Jianzhu University, Shenyang 110168, Liaoning)

Selection of swimming athletes is a typical assignment problem worthy of studying. In this paper, the problem is turned into a general linear programming problem and solved by mathematical software, achieving a good effect.

assignment; linear programming; mathematical software

2014-10-24

2014-11-10

隋 英(1974～)，女，副教授.E-mail:2008suiying@163.com

O173

A

1671-3524(2015)02-0083-03