一种基于矢量的无线基站驻波比检测方法
张宏伟, 贺菲菲, 王博明
(中兴通讯股份有限公司 西安研发中心, 陕西 西安 710065)
一种基于矢量的无线基站驻波比检测方法
张宏伟, 贺菲菲, 王博明
(中兴通讯股份有限公司 西安研发中心, 陕西 西安 710065)
给出一种基于矢量的无线基站驻波比检测方法,并根据无线基站硬件架构给出矢量驻波检测的数学模型和误差来源,以及在时域上获取信号的幅度和相位信息。通过测量3种状态下的 S 参数,利用蒙特卡罗算法计算系统误差,最后应用电磁仿真技术完成模型的仿真。实例验证结果表明,与标量驻波比检测方法相比,所给方法提高了测量精度,从理论模型、实现机制上都具有较高的准确性和鲁棒性。
矢量驻波比;无线基站;S参数
高效率传送功率是通信系统的一个基本问题之一。在无线通信中,天线与馈线的阻抗不匹配或馈线与基站发射机的阻抗不匹配,发出去的能量就会产生反射折回,反射波与前进的正向波汇合就会发生驻波。
驻波的大小影响基站的辐射效率,另外反射回来的电波最终会变成热量,使得馈线升温。它在发射机输出口也可产生相当高的电压,有可能损坏发射机。
驻波比全称为电压驻波比(Voltage Standing Wave Ratio ,VSWR)。它是射频技术中最常用的一个参数或数值,用来衡量射频部件之间的匹配是否良好。
现阶段驻波比的检测主要采用标量驻波比检测方法,这种方法直接对检测点的反射信号进行模拟采样,计算相应的功率值或能量值,然后计算待测点的入射能量和反射能量之比,从而得到对应的驻波比。其主要优点是实现简单方便,实现检测无需提前获取系统的校正参数。存在的缺陷是没有考虑入射和反射信号的相位特性,造成测量值无法直接映射到天馈端口,所以就不能真正反映天馈端口的驻波比状况。
VSWR检测处于发射通道的对外接口,是基站对外连接状态的指示器。驻波比必须小于某个门限,对于超过门限的情况必须进行告警,同时对设备采取相关的保护措施。实现告警处理的前提是驻波比检测必须准确和可靠,避免错报和误报。
在无线网络中,由于环境的复杂性,容易受到激励信号的随机波动和外界干扰的影响,如何即准确又可靠的VSWR检测,是评价无线网络性能的一项重要指标。
本文以驻波比理论为基础,采用多样本的测试验证,提出一种准确有效的驻波比检测方法。结合仿真和计算,给出了一种矢量驻波比检测的实现方法。
1 理论分析
VSWR不是一个直接测量值,而是一个通过反射系数Γ求得的计算值,其表达式为[1]
式中Γ表示反射系数,通过入射信号和反射信号求得,表达式为[2]
其中VREV为反射信号电压,VFWD为入射信号电压,PREV是一段时间内反射平均功率,PFWD是相同时间段内入射平均功率。反射系数Γ是一个大于零的实数,所以VSWR的值是一个大于1的数值。
在实际应用中,不是通过直接测量电压来表征VSWR,而是用等效的回波损耗RL(Return Loss)来表示,RL表征的是在待测端口观测的入射能量和反射能量之比,表达式为[3]
其中回波损耗单位为dB,回波损耗与反射系数的关系式为
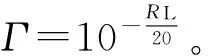
在理想状况下,反射系数Γ等于0,驻波比则为1。但实际上总存在反射,所以驻波比总是大于1的。
2 驻波比检测方法
在无线基站的硬件架构中,驻波比的检测框图[4]如图1所示。

图1 基站发射机的前反向功率检测连接图
前向功率(Forward Power,FWD)检测取样位置在功放(Power Amplifier ,PA)的输出端末级功放管和环行器之间,反射功率(Reverse Power, REV)检测取样来自环行器的隔离端的耦合输出。这样两个取样信号都不是来自于基站的天馈端口,是真实输出位置。在驻波比检测位置和天馈之间存在一个无源射频模块(Radio Frequency Module ,RFM),它包括环行器、双工器、射频线缆和射频连接器等,而这些无源器件的特性,如隔离度、连接状态等都会影响真实基站的驻波比状态。
为了真实反映驻波比的状态,需要把当前驻波比检测位置(在基站内部)映射到天馈口(在基站外部),考虑到RFM的影响,可以把驻波比检测硬件电路等效为一个双端口的网络,如图2所示。
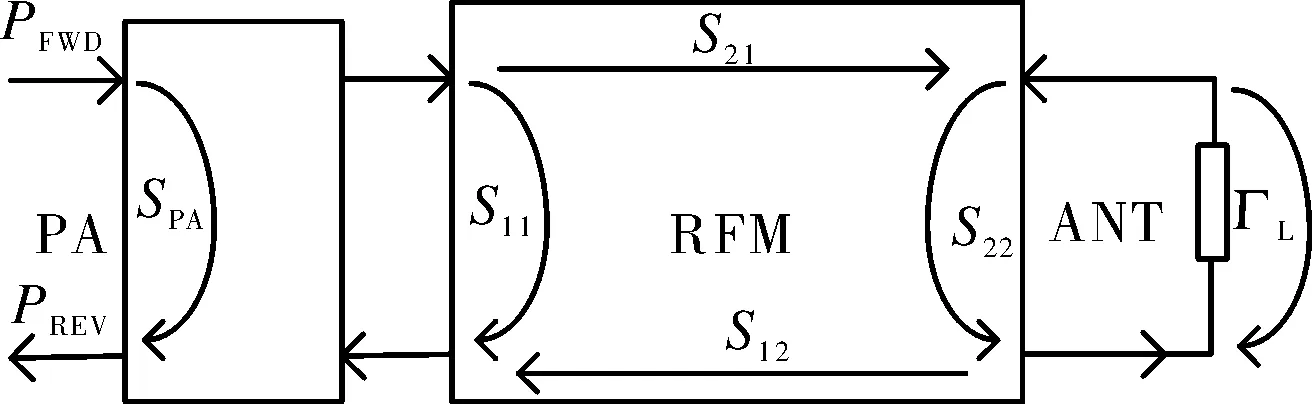
图2 基站前反向功率检测等效网络示意图
图2中的射频模块RFM主要是无源部件,包括环形器、双工器、射频线缆和射频连接器等。其中RFM的影响等效为网络中的S12、S21、S11、S224个S参数。SPA为实际测量到的PA端(发射口)反射系数,ΓL为天馈口的反射系数,可以看出,在一般情况下,SPA≠ΓL。
根据能量守恒原理[3]有
(1)
由式(1)可以得到天馈口的反射系数为
(2)
其中ST=S12S21。
由式(2)可知,当SPA已知时,想求出ΓL需要3个独立的方程式求出ST、S11、S22这3个未知数,通过在天馈口连接3个特殊负载(开路、短路、匹配)来进行计算求解。但是对于基站而言,提供大功率的这3个特殊负载是很困难的。可以用3个已知的有明显差别的经过校准的负载(分别模拟开路、短路、匹配)进行标定,形成3个方程,求得3个未知的传输参数,从而建立ΓL和SPA的映射关系[5]。
具体推导结果为
(3)
其中
A=ΓL1ΓL2SPA3(SPA1-SPA2)+ΓL1ΓL3SPA2(SPA3-SPA1)+ΓL2ΓL3SPA1(SPA2-SPA3),
B=ΓL1ΓL2(SPA1-SPA2)+ΓL2ΓL3(SPA2-SPA3)+ΓL1ΓL3(SPA3-SPA1),
则有
(4)
(5)
其中ГL1、ГL2和ГL3分别是已知的3个校准负载对应于50 Ω标准端口的反射系数,SPA1、SPA2和SPA3是3个已知负载对应求得的待映射的反射系数。
SPA1、SPA2和SPA33个反射系数是通过矢量计算得到的,其反射系数计算公式为[2]
(6)
其中R是反向检测矢量,F是前向检测矢量。式(6)中的这两个测试值理论上要求是同时采样和计算的。所以,在矢量驻波比检测中,需要解决时延对齐的问题。
从图3中可以看到,基站的前向功率(FWD)检测和反射功率(REV)检测电路是共享反馈通道(PRX)的,通过一个模拟开关来分别检测,这样反射信号和入射信号不能同时处理,也就是说一次采样是无法做到时延对齐,所以需要引入一个宽带的参考信号(REF),在参考信号(REF)分时做两次激励,这两次激励的信号特征(带宽,峰均比等)基本相同,但由于是宽带信号,两次激励信号的幅值和相位存在差异的;在激励下分别做两次采样工作,分别得到FWD信号和REV信号的采样均值MFWD和MREV,这两组数据的初始相位是需要对齐的。

图3 前反向功率检测共享反馈通道(PRX)示意图
第一次采样,激励信号REF通过发射(Transmitter ,TX)通道发送一组数据,这组数据表征为T1,在一定的固定延时后, 反馈通道(PRX)切换到FWD通道,采样就会得到一组(N个)FWD值,并做均值为
(7)
第二次采样,激励信号REF通过TX(发射)通道发送一组数据,数据表征为T2,反馈通道开关切换到REV通道,同样REV的矢量均值为
(8)
其中F(I(n)+Q(n))和T(I(n)+Q(n))分别表示前向和基带第n个点的矢量值,N是采样的点数。
假定FWD和REV的采样通道增益在两次采数之间变化可以忽略不计(这要求两次采数之间的时间间隔尽量的短),即T1和T2相通。由式(7)和式(8)可得
(9)
通过式(2)、式(3)、式(4)、式(5)和式(9)计算可以得到ΓL,并可由式(1)得到天馈口电压驻波比。
需要说明的是,上述计算是在基站内部的FPGA、DSP和CPU协同工作完成的。
3 仿真和分析
3.1 仿真模型
驻波比检测电路的前向功率检测(FWD)端口一般放在功放上末级管后环形器前,反向功率检测(REV)端口一般有两种位置。无论那种状态,驻波比检测电路结构可以看成由功放管输出、天馈输出口、FWD检测口和REV检测口4端口网络组成。
根据以上硬件架构,可以把这个4端口的微波网络等效成信号流图[6],如图4所示。

图4 等效信号流图
矢量驻波比检测时,可获取数据为REV和FWD的比值
(10)
根据图4的信号流,可以推导SM和天线口反射系数Γ的关系为
上式可以简化成
(11)
其中A、B、C为变量;要得SM和Γ的具体关系,就需要对A、B、C三个变量求解。可以看到,前面实现方案描述的驻波比计算是推导式(11)的一个例子。
对于A、B、C3个未知数,可以通过天线口3种状态获得对应的SM,解方程得到A、B、C的值。为了便于仿真,采用匹配负载、开路、和短路3种情况[2,7]
(12)
在校测过程中误差的产生原因有3个。
(1) 匹配负载、开路、短路校准时,连接器连接、负载特性等不确定性导致的误差;
(2) 计算SM时,基站内部模拟采样、数字处理等在相位对齐时产生的误差;
(3) 环境变化(温度等)对检测通道的影响产生的误差等。
3.2 仿真过程
对系统的驻波比检测仿真,需要在校准、驻波比检测、驻波计算等过程中相应加入误差模型,通过蒙特卡罗等算法获取多个样本,然后计算出整个过程的误差。
首先对匹配负载、开路、短路3个校准过程进行建模。这里误差设定为
(1) 负载和连接器特性的幅度误差±0.1dB,相位误差±3度。
(2) 数字处理的相位检测误差±10度。
3.2.1 驻波比校准模型
驻波比校准原理如图5 所示[8]。

图5 驻波比校准原理
该模型在短路、开路和匹配负载的条件下,得到一组在不同频率下的S参数。仿真结果如图6所示。
3.2.2 驻波比检测模型
驻波比检测原理[9]如图7所示。

图7 驻波比检测原理
该模型通过对多个样本的采样,得到多组FWD和REV的矢量值。
3.2.3 驻波比计算
根据式(2)、式(3)、式(4)、式(5)和式(9),使用上面校准和驻波比检测的仿真数据,对驻波比进行检测运算。计算结果如图8所示。

图8 驻波计算结果
从图8中可以看出,系统的驻波比检测误差随着被测件的驻波比的增大而增大,整体呈光柱发散形状;当驻波比在2.5以内时,误差区间为±0.2。
在被测天馈口驻波比为2.0时,频率维度和仿真统计直方图如9所示。
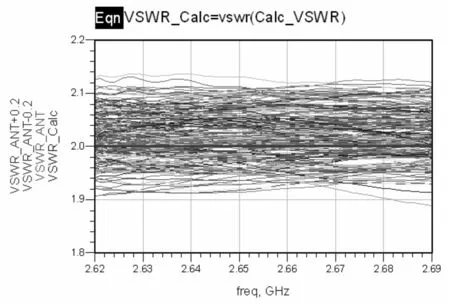
(a) 频率维度

(b) 直方图
以被测天馈口驻波比为3.0时,频率维度和仿真统计直方图如图10所示。

(a) 频率维度
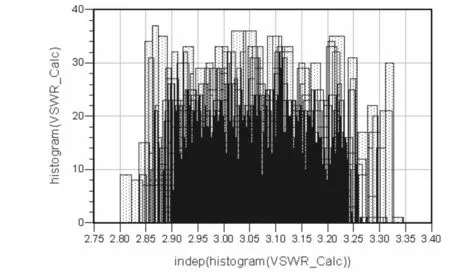
(b) 直方图
可以看出,当被测天馈口驻波比小于2.0时,常温下基本可以保证检测精度±0.2,当被测天馈口驻波比大于3.0时,就无法保证±0.2精度。如果考虑温度等环境因素的影响,误差会更大。
4 实验验证
以上理论和仿真结果,优化的结果应用在基站的大样本实验环节,来进一步对该方法进行验证。
(1) 实验校准
通过生产线工装来实现校准和验证,其示意图如图11所示。

图11 生产线工装示意图
该工装包含3个校准负载(1个匹配负载,1个模拟开路负载,1个模拟短路负载)和1个验证负载(驻波比2.0~3.0)、大功率电子开关、1个控制板。
首先用矢量网络分析仪将3个负载在使用频段内扫描一遍,记录下反射系数和频率的关系,以便后面校准的时候调用。
校准时,逐频点进行3个已知负载的测试,然后求出该频点对应的3个S参数分量,将其保存到文件。此文件是一个频点和反射系数的二维表。
(2) 验证
基站启动,加载校准文件,配置相应频点,生产线工装切换到验证负载,读取REV和FWD值,按照上述计算方法得到矢量驻波比。
在后台软件上,和在该频点下验证负载的实际驻波比值进行比较,验证该驻波比检测的准确性。
对近19 899个有效样本进行统计分析,提取驻波比为2.0@2130MHz的验证负载时,对应的矢量驻波比计算值,结果如图12所示。

(a) 驻波比测试结果

(b) 2.1G频段驻波比测量值分布及GCF
从数据上可以看出,矢量驻波比值与真实值误差在+0.25 ~ -0.20 之间,并且分布比例基本呈正态分布状态。这个结果和前面仿真的结果是一致的。
5 结束语
通过模拟矢量网络分析仪检测原理,提出了一种基于矢量的驻波比检测方法,在时域上获取信号的幅度和相位信息,建立校准和检测两种模型。通过测量三种状态下的 S 参数,利用蒙特卡罗算法计算系统误差。充分考虑了信号的相位特性,从而相对于标量测量,提高了测量精度。
利用仿真的方法对模型进行了计算,对驻波比进行了约束,保证了测量精度。通过多样本的实验验证,结果证明本方法是一种准确有效的驻波比检测方法。
[1] 雷振亚.射频/微波电路导论[M].西安:西安电子科技大学出版社, 2005:218-236.
[2] Agilent technologies.Time Domain Reflectometry Theory[M].Agilent technologies University :Agilent technologies, 2013:5965-4855.
[3] Agilent technologies.Exploring the Architectures of Network Analyzers[M]. Agilent technologies University: Agilent technologies, 2000:5965-7708E.
[4] Agilent technologies.Applying Error Correction to Network Analyzer Measurements [M]. Agilent technologies University:Agilent technologies, 2002:5965-7709E.
[5] 陈 斌,赵 鹏,杨路刚,等.基于RWG矩量法的短波天线辐射性能分析[J].西安邮电大学学报,2014,15(5):96-100.
[6] 王华华, 吕 南, 张 莉. 一种改进的上行信道估计算法[J].西安邮电大学学报,2014,15(1):21-25.
[7] 孙友伟, 董建姣, 基于电力线的自适应阻抗匹配方案[J].西安邮电大学学报, 2013,15(6):38-42.
[8] 赵克玉,许福永.微波原理与技术[M].北京:高等教育出版社,2006:15-106.
[9] 战金龙,方会妮,郑亮.长期演进系统上下行信号识别算法[J].西安邮电学院学报,2012,17(2):9-12.
[责任编辑:祝剑]
A vector standing wave ratio detection method of wireless base stations
ZHANG Hongwei, HE Feifei, WANG Boming
(ZTE Corporation, Xi’an R&D Center, Xi’an 710065,China)
A VSWR(Vector Standing Wave Ratio)detection method based on vector is proposed in this paper. Base on the present wireless base stations hardware architecture, a mathematical model of VSWR detection and error sources is provided to obtain the signal amplitude and phase information in time domain. By measuring of “S” parameters under three conditions, the error of the whole system is calculated by using Monte Carlo method. The simulation of the model is then carried out by using electromagnetic simulation technology. Experiments results show that compared with scalar VSWR method, this method has high accuracy and robustness at the theoretical model and the implementation mechanism.
vector standing wave ratio, wireless base stations, S parameters calibration
2015-04-07
张宏伟(1972-),男,硕士,高级工程师,从事移动通信测试技术及仿真技术研究。E-mail:zhang.hongwei3@zte.com.cn 贺菲菲(1980-),女,硕士,工程师,从事移动通信终端产品软件协议研究。E-mail:he.feifeixa@zte.com.cn
10.13682/j.issn.2095-6533.2015.05.005
TN98
A
2095-6533(2015)05-0028-06

