胶泥缓冲器的非线性刚度的控制机理研究*
徐忠四,刘卫新,杜文建
(1.中北大学机电工程学院,太原 030051;2.北方自动控制技术研究所,太原 030006;3.奇瑞汽车股份有限公司产品开发管理中心,安徽 芜湖 241009)
胶泥缓冲器的非线性刚度的控制机理研究*
徐忠四1,刘卫新2,杜文建3
(1.中北大学机电工程学院,太原 030051;2.北方自动控制技术研究所,太原 030006;3.奇瑞汽车股份有限公司产品开发管理中心,安徽 芜湖 241009)
为了改善履带车辆悬挂系统在各种路面的平顺性和缓冲性,对悬挂系统匹配了一款具有非线性刚度的粘弹性胶泥缓冲器。为了定量地研究胶泥缓冲器的非线性刚度控制机理,建立了非线性悬挂系统的动力学方程组。提出了一种无条件稳定的线性加速度逐步积分法对非线性方程组进行数值求解的新方法,最后用冲击实验验证该方法的可靠性。该研究为胶泥缓冲器的优化设计和车辆悬挂悬挂系统的动力学匹配提供了理论指导。
非线性刚度,胶泥缓冲器,冲击实验,控制机理
0 引言
粘弹性胶泥缓冲器是履带车辆悬挂系统的一个部件,对车辆平顺性、缓冲性和悬挂系统的正常工作有着至关重要的作用。设计粘弹性胶泥缓冲器时,最关键的是要建立阻抗力与活塞位移和速度之间的数学模型,其中的刚度与阻尼也随着活塞位移和速度发生变化。该本构关系是一非线性泛函,具有明显的非光滑、强非线性特性[1]。
目前,纯粘滞性的胶泥缓冲器[2-3]国内外研究较多,而粘弹性的胶泥缓冲器则研究较少,单出杆式的胶泥缓冲器是本文的研究对象,其数学模型的研究仍然处于初级阶段[4-6],Jarret给出的单出杆式胶泥缓冲器的数学模型将缓冲器当作线性刚度,与实际情况有差别,文中基于相关的理论与合理的假设[7-9],结合胶泥缓冲器的使用环境,建立了装有胶泥缓冲器的非线性悬挂系统的动力学方程组,定量地研究非线性悬挂的非线性刚度变化规律,提出了一种无条件稳定的线性加速度逐步积分法对非线性方程组进行数值求解的新方法,最后用冲击实验验证该方法的可靠性。
1 装有胶泥缓冲器的悬挂系统的动力学方程组
多数情况下,在研究车辆悬挂系统的时候,一般都把它简单表达为单轮车辆悬挂系统模型,并简化为二自由度系统,其两个自由度分别是簧上质量和簧下质量的垂直振动。以下为悬挂系统工作的两种状况:
①缓冲器未受到撞击时,缓冲器不起作用,只有单个减振器起作用。这时单个负重轮模型的动力学方程为:

在式(1)中,ms为簧载质量;mu为非簧载质量;Ks为悬挂弹簧刚度;Ku为负重轮刚度;cs为减振器阻尼系数;x2为簧载质量位移;x4为非簧载质量位移;q为路面激励位移。
②平衡肘撞击缓冲器时,缓冲器起附加减振器和弹簧的作用,这时悬挂系统的刚度相当于两个弹簧并联(合并后刚度Ksh=Ks+Kh;Kh缓冲器刚度),阻尼也相当于并联(合并后阻尼C=Ch+Cs;缓冲器阻尼)。单个负重轮模型的动力学方程为:

缓冲器被撞击时,二自由度悬挂系统模型图如图1所示。

图1 缓冲器被撞击二自由度悬挂系统模型
2 非线性悬挂系统动力学方程的数值求解
2.1 非线性悬挂系统动力学增量平衡方程
当平衡肘撞击缓冲器时,这时悬挂系统的刚度随着负重轮的位移是不断变化的,这时的悬挂系统为非线性悬挂系统,建立的方程组(2)为非线性方程组,下面用逐步积分法介绍求解过程。

在时刻t+Δt,非线性悬挂系统动力学方程为
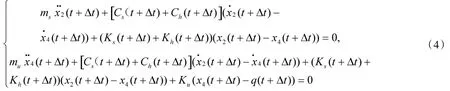
将式(4)减去式(3)对应的各式,可得到非线性方程组的增量平衡方程组如下。
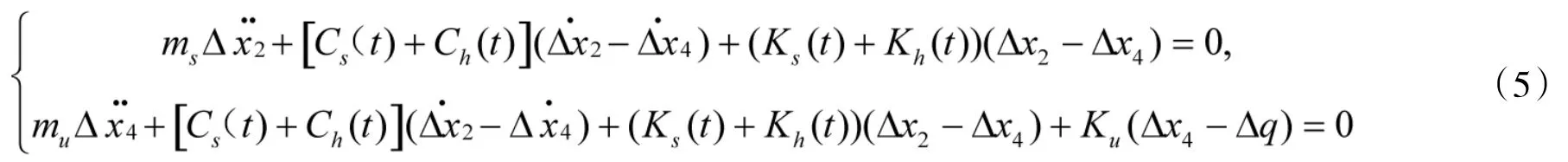
在式(5)中,
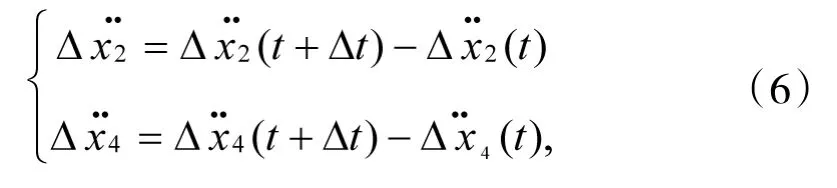


在非线性悬挂中,悬挂的弹性力和阻尼力分别用Ffs,FfD表示,悬挂系统的刚度和阻尼在Δt很小时,在区间(t,t+Δt)变化很小,可以近似地取为。

将式(6)~式(9)代入式(5),可得到非线性悬挂系统的动力学增量平衡方程的矩阵形式如下:

式(10)中,[M]:质量矩阵;[C(t)],[K(t)],[Ku]:时刻t的悬挂阻尼矩阵,刚度矩阵和轮胎的刚度矩阵;增量加速度,增量速度,增量位移;{Δq}:增量地面激励向量。
现在将增量位移和增量速度的计算方法,根据泰勒级数展开,可写出:

2.2 无条件稳定的线性加速度逐步积分法
下面采用线性加速度法,在时间区间(t,t+Δt)认为加速度增量与时间增量成比例,也就是略去加速度增量中(Δt)2及其以上项,当Δt较小时,增量位移和增量加速度有足够的准确性,在以上假设条件下,可知

将式(12)代入非线性悬挂系统动力学增量平衡方程,得到

整理并项后,得到

由式(14)可得到增量位移向量公式为
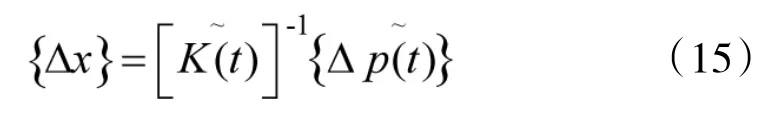
将式(15)代入式(12),便可得到增量速度向量的表达式为。


在时间步长τ的情况下,计算有效动力刚度矩阵,有效增量载荷向量,上述表达与在形式上完全相同,只不过是用τ代替Δt,因此,得到延长步长τ情况下的增量位移向量计算公式

进而可得

按照线性加速度的原理有

3 实验结果与分析
本项目所用的粘弹性胶泥缓冲器的基本设计参数如表1所示。Lg为活塞杆的长度。
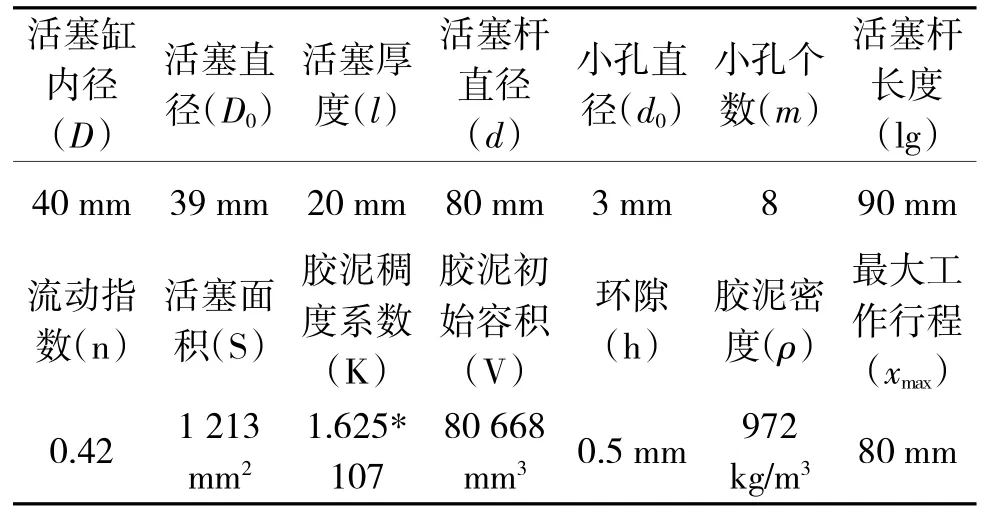
表1 粘弹性胶泥缓冲器的基本参数
在上述基本参数下讨论无条件稳定的逐步积分法,数值积分方法可能引起的误差依赖于系统的动力特性和所取的时间步长Δt,垂直线振动的固有频率约在1.5 Hz左右,车轮垂直振动的固有频率约为30 Hz左右。为使悬挂系统数值分析较为准确,时间步长选择依据下面计算公式:
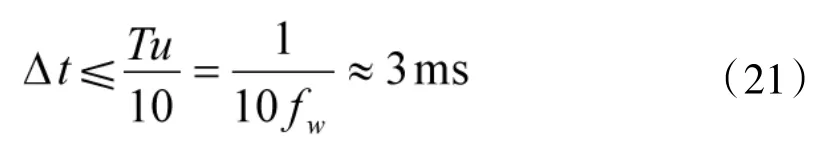
根据上面的无条件稳定的线性加速度逐步积分法,取时间步长Δt=2.5 ms,可得到缓冲器的刚度Kh与压缩位移x之间的关系式

上式中,缓冲器的刚度Kh的单位为N/mm,压缩位移x的单位为mm。
对(22)方程的两边对x进行求导,可得

由式(23)可知,刚度的斜率恒大于零,表明缓冲器的非线性刚度是随着压缩位移的增加而快速增加的,即缓冲器的刚度表现出一种渐升特性。缓冲器刚度的渐升特性将为缓冲器的设计和动力学建模提供理论依据。
为了验证上述方法所建立的缓冲器的非线性刚度的控制机理能否可靠地描述缓冲器的工作特性,将所设计的胶泥缓冲器安装在模拟军用车辆悬挂系统工作环境的冲击试验台上进行冲击实验。制作了一个质量m=200 kg的锤头及固定缓冲器基座,测量设备和缓冲器的安装示意图如图2所示。

图2 冲击试验安装示意图
根据加速度传感器的工作原理,只有跌落锤和缓冲器的活塞杆接触时才会有信号,所以将跌落锤的加速度、速度和位移可以近似为缓冲器活塞的加速度、速度和位移。以跌落锤与活塞杆接触时刻为记时起点,得到的位移即为缓冲器的行程,跌落锤的加速度与质量的乘积近似为缓冲器的弹性回复力。
弹性回复力,主要是活塞压缩胶泥而产生的。当胶泥缓冲器的活塞开始压缩胶泥时,胶泥被压缩产生压强,设其压缩率为δ,压强为Pδ,活塞的端面面积为S,则胶泥产生的弹性回复力的大小为:

胶泥的压缩率可以根据活塞的结构尺寸及活塞的位移求得:

在上式中,x为活塞压缩位移,V为未压缩时胶泥的体积。
由无条件稳定的线性加速度逐步积分法得到的理论拟合曲线和缓冲器冲击实验得到的胶泥的压强与压缩率对比关系曲线如图3所示,试验数据与理论拟合曲线的吻合度非常高,说明无条件稳定的线性加速度逐步积分法对胶泥缓冲器的非线性刚度进行控制是可靠的。

图3 胶泥压强与压缩率的关系曲线
4 结论
①试验数据与理论拟合曲线的吻合度非常高,说明无条件稳定的线性加速度逐步积分法对胶泥缓冲器的非线性刚度进行控制是可靠的;②用无条件稳定的线性加速度逐步积分法得到了缓冲器的刚度与压缩位移之间的关系式:缓冲器的非线性刚度是随着压缩位移的增加而快速增加的,即缓冲器的刚度表现出一种渐升特性;③胶泥缓冲器的非线性刚度的控制机理,将会对胶泥缓冲器的优化设计和车辆悬挂系统的动力学匹配计算提供理论指导。
[1]徐忠四.粘弹性胶体缓冲器非线性时滞动力系统建模及随机最优控制研究[D].太原:中北大学,2013.
[2]Jia J H,Shen X Y,Hua H X.Viscoelastic Behavior Analysis and Application of Fractional Derivative Maxwell Model[J]. Journal of Vibration and Control,2007,13(4):385-401.
[3]Karavasilis L T,Ricles M J.Experimental Evaluation of the Seismic Performance of Steel MRFs with Compressed Elastomer Dampers Using Large-Scale Real-Time Hybrid Simulation[J].Engineering Structures,2010,33(6):1859-1869.[4]贾九红,黄修长,杜俭业,等.粘滞型胶泥吸能器建模与实验分析[J].噪声与振动控制,2007(5):31-33.
[5]张同忠.粘滞阻尼器和铅阻尼器的理论与试验研究[D].北京:北京工业大学,2004.
[6]Hyo J K,Wan S Y,Jin K O,et al.Parameter Identification of Damping Models in Multibody Dynamic Simulation of Mechanical Systems[J].Multibody Syst Dyn,2009(22):383-398.
[7]Chang T S,Singh M P,Asce F.Mechanical Model Parameters for Viscoelastic Dampers[J].Journal of Engineering Mechanics,2009,135(6):581-584.
[8]Chen C,Ricles J M,Marullo T,et al.Real-time Hybrid Testing Using the Unconditionally Stable Explicit CR.Integration Algorithm[J].Earth quake Engineering and Structural Dynamics,2009,38(1):23-44.
[9]陈爱华.三维非线性粘弹性动力学方程组的时间周期解和行波解[D].上海:复旦大学,2008.
[10]Dong X M,Miao Y,Liao C R.A New Variable Stiffness Absorber Based on Magneto-Rheological Elastomer[J].Transactions of Nonferrous Metals Society of China,2009,19(3):611-615.
[11]Lu L Y,Lin G L,Shih M H.An Experimental Study on a Generalized Maxwell Model for Nonlinear Viscoelastic Dampers Used in Seismic Isolation[J].Engineering Structures,2012,34(1):111-123.
Research on Control Mechanism for Nonlinear Stiffness of Elastomer Damper
XU Zhong-si1,LIU Wei-xin2,DU Wen-jian3
(1.School of Mechatronic Engineering,North University of China,Taiyuan 030051 china;
2.North Automatic Control Technology Research Institute,Taiyuan 030006,china;
3.Product Development and Management Center,Chery Automobile Co,Ltd.Wuhu 241009,China)
In order to improve the ride and dampening performance of tracked vehicle’s suspension system in all kinds of roads,a viscoelastic elastomer damper with nonlinear stiffness is matched for the suspension system.Dynamical equation sets of nonlinear suspension system are built to study the control mechanism of nonlinear stiffness of elastomer damper quantitatively.A new method of linear acceleration successive integration method with no condition stability is proposed to make the numerical solution for the nonlinear equation sets.Finally,the reliability of the above method is validated through the shock experiments.All of which will provide the theoretical guide for the optimal design of the elastomer damper and dynamic matching research between the elastomer damper and the vehicle’s suspension system.
nonlinear stiffness,elastomer damper,shock experiment,control mechanism
TB11
A
1002-0640(2015)05-0179-05
2014-03-06
2014-04-24
国家自然科学基金资助项目(50976108)
徐忠四(1977- ),男,湖北通山人,博士,讲师。研究方向:车辆动力学建模与仿真。

