基于向量皮尔森相关系数的组合赋权法

张 峰，谢振华，程江涛，崔高仑，徐衡博

（1.海军航空工程学院青岛校区，山东 青岛 266041；2.解放军91033部队，山东 青岛 266071）

基于向量皮尔森相关系数的组合赋权法

张 峰1，谢振华1，程江涛1，崔高仑1，徐衡博2

（1.海军航空工程学院青岛校区，山东 青岛 266041；2.解放军91033部队，山东 青岛 266071）

针对多属性决策中属性权重的确定问题，提出了一种基于皮尔森相关系数的主、客观权重的集成方法。用权向量的相关度作为不同赋权方法重要性的度量，意义明确，计算简单，可操作性强。最后采用算例验证了此方法的有效性和实用性。

多属性决策，组合赋权，皮尔森相关系数，相关度，权重

0 引言

多属性决策是与多个属性有关的有限方案选择问题，广泛存在于经济、社会、工程、管理等诸多领域决策中［1］，合理确定属性权重成为多属性决策的一个重要研究内容。目前，确定权重的方法主要有两类：主观赋权法和客观赋权法，前者依赖决策者的经验和判断，反映了决策者的主观评价，解释性比较强，但失之于随意性大；后者按特定方法客观处理指标信息，传递属性所包含的决策信息量，但忽略了决策者的主观认知。为获得合理评价结果，许多学者将主客观赋权法有机结合，提出了组合赋权思想和方法。

由于主观赋权方法和客观赋权方法都有各自的优缺点，所以很多学者提出了综合主、客观赋权法的组合赋权法、交互式赋值法、组合TOPSIS方法等［2-5］。文献［6］基于使各决策方案的多属性综合评价值尽可能分散便于方案的鉴别和排序的基本思想，以离差平方和为准则建立最优赋权方法。文献［7］提出了一种最佳组合赋权方法，利用加权偏差平方和最小化准则给出了最佳组合权重的线性表达形式，并用广义一致性准则和TOPSIS法来求解最优组合权重系数，但是针对TOPSIS法存在距离正理想解近的方案未必距离负理想解远以及各指标间存在不同程度的相关性的问题，因此，不加改进应用TOPSIS法是不科学的。此外，此方法计算繁琐，不易理解。文献［8］为了能最大化不同地被评价对象之间的差异，建立了方差最大化模型。文献［9］提出了基于最小离散和最大广义联合熵的组合赋权方法，但是计算量大，失之于繁琐。文献［10］提出了基于最小离差和最大广义联合熵的组合赋权方法。文献［11］提出了一种新的多属性决策权重集结方法，但在处理单目标规划时，对熵和相对熵的偏好系数赋值时主观随意性大。

总之，现有的组合赋权法或者计算复杂，或者没有进行一致性检验而缺乏一定的科学性。为此，本文提出基于皮尔森相关系数［12-14］的思想，建立了基于皮尔森相关系数的组合赋权方法计算模型，并以导弹质量评估实例对模型进行了验证，结果说明该方法是合理的。

1 原理与方法

1.1 多属性决策方法原理

在多属性决策模型中，方案集S={S1，S2，…，Sm}，属性集P={P1，P2，…，Pn}，属性权重集合；式中：，0＜ωj＜1。决策矩阵A=［aij］m×n， aij是方案Si在属性Pj下的评价值。通常，属性有效益型、成本型、固定型及区间型几种，并且不同属性的量纲可能也不同，为便于计算，必须对决策矩阵进行规范化。设决策矩阵为经无量纲化处理所得到的矩阵B=（bij）m×n，该矩阵称为规范化的决策矩阵。

1.2 权重的确定

1.2.1 主、客观赋权方法确定的权重

决策者选择l种主、客观赋权法分别确定的指标权重为：

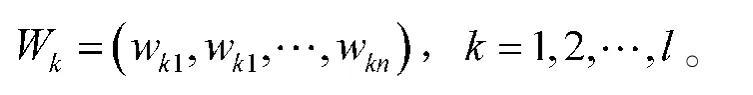
1.2.2 主、客观组合赋权法

将主、客观赋权法相组成，实现主观和客观的统一，可得如下组合赋权权重向量：

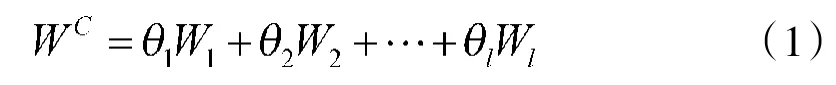
式中：WC为组合赋权权重向量，其中θ1，θ2，…，θl为组合系数，θk≥0，。

令W=（W1，W2，…，Wl），Θ=（θ1，θ2，…，θl）T，则式（1）可以表示为：

依据线性加权法［15］，由组合赋权向量计算而得到的第i个决策方案Si的多属性决策评价值为：

1.2.3 皮尔森相关系数计算［16］

PCC是一种线性相关系数，它反映两个变量间的线性相关程度［17］。设对于任意两随机变量X={x1，x2，…，xn}，Y={y1，y2，…，yn}，PCC（X，Y）定义如下:

式中：x，yi分别是X，Y的均值。PCC（X，Y）取值在-1～1之间。当PCC（X，Y）为-1或1时，表示两个变量完全相关；PCC（X，Y）为0时，表示两个变量线性无关。

为了便于比较衡量，现将PCC（X，Y）值进行如下改进。

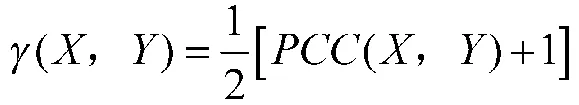
由上式可知：

①非负性。γ（X，Y）∈［0，1］；

②对称性。γ（X，Y）=γ（Y，X）；

③当γ（X，Y）=1时，两随机变量完全相关；

④当γ（X，Y）=-1时，两随机变量完全不相关。

1.2.4 基于皮尔森相关系数的组合赋权法

通常用主、客观赋权法计算所得的权重向量是不相同的，从线性相关原理分析，有的权重向量相关程度比较高，有的相关程度比较低。如果一种赋权法所得的向量与其他赋权法所得的向量相关程度大，则说明多数决策者持有相近的主观偏好或由原数据处理得到的权重比较稳定可靠，这些权向量在组合权向量中应获得更大的比重。因此，可以通过权重向量与其他权重向量总相关度的相对大小来度量各种赋权方法的相对重要性。

任一权重向量Wk与其他向量总相关度为：

式中：k=1，2，…，l

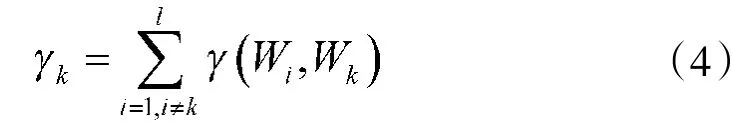
因此，任一权重向量的权系数向量为：

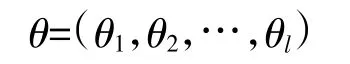
式中：k=1，2，…，l

1.2.5 组合赋权法的事后检验

计算各种组合赋权向量与各种主客观赋权向量之间的广义相似系数，并取其平均值作为事后检验的标准，平均值越大，组合赋权法越好。为便于计算，本文采用向量s和t之间的绝对距离来度量向量的相似性。定义赋权向量s和t之间基于绝对距离的广义相似系数［7］为：

由广义相似系数的定义可知：0≤est≤1。

2 算例分析

为了便于比较分析，本文选用文献［18］中的算例。某型导弹定期检测维护，以其突防系统为例，基于皮尔森相关系数的组合赋权方法的多属性决策方法，实行突防系统质量动态评估。某次检测数据与前几次检测数据量化指标如表1所示：

第1步：计算权重向量与其他向量总相关度根据式（4）计算得：

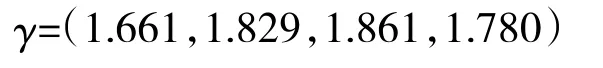
第2步：计算权重向量的权重系数向量

根据式（5）可得组合权重系数向量为：

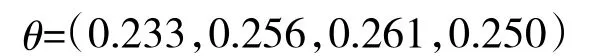
第3步：计算组合权重

根据式（1）可得组合权重为：

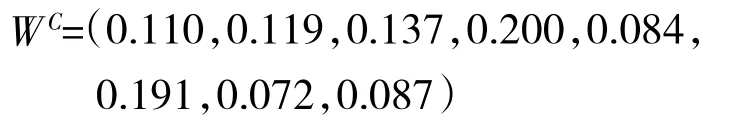
第4步：组合赋权法的事后检验

根据式（6）可得组合权重与原来的4种主、客观赋权法之间的平均广义相似系数取值都在0.872以上，基本保持一致。

第5步：计算多属性决策评价值进行质量动态评估

根据式（3）得各个时间的突防系统综合评估值为：

第6步：评价结果分析

由表3可知单纯采用主观赋权法（AHP法、Delphi法）进行动态评估，所得的动态评估综合评价值区分度不太好，以致于在实际的导弹质量动态评估中不利于决策。而单纯采用客观赋权法（熵权法、离差最大化法）进行动态评估，没有充分利用长期积累起来的经验知识。基于皮尔森相关系数法的组合赋权法所得的动态评估值与采用最优权系数法的动态评估值基本一致，说明本文采用的方法的正确性。

表1 导弹突防系统性能检测参数量化指标值

表2 各种赋权方法所得指标权重

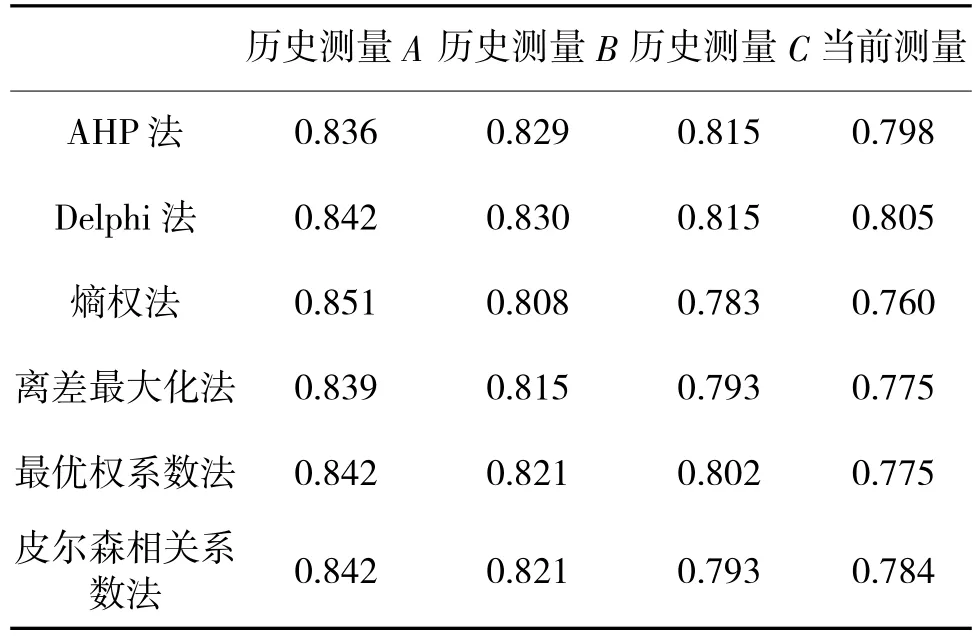
表3 各种赋权方法所得突防系统综合评估值

3 结论

如何对各种主、客观赋权法所得的权重向量进行组合一直以来是研究的热点，本文提出了一种基于皮尔森相关系数法的组合赋权方法，方法易于理解和计算。对导弹的突防系统的质量评估算例进行了仿真验证，得到了正确的结论，说明了方法的合理性。此外，该方法丰富了处理多属性决策问题的方法，拓展了此领域的研究空间。

［1］Hwang C L，Yoon K.Multiple Attribute Decision Making：Methods and Applications［M］.New York:Springer-Verlag，1981：1-10.

［2］Wang T C，Lee H S D.Developing a Fuzzy TOPSIS Approach Based on Subjective Weights and Objective Weights［J］.Expert Systems with Applications，2009，36（5）：8980-8985.

［3］Xu X Z.A Note on the Subjective and Objective Integrated Approach to Determine Attribute Weights［J］.European Journal of Operational Research，2004，156（2）：530-532.

［4］Wang Y M，Luo，Y.Lntegration of Correlations with Standard Deviations for Determining Attribute Weights in Multiple Attribute Decision Making［J］.Mathematical and Computer Modelling，2010，51（1-2）：1-12.

［5］Fu C，Yang S L.An Attribute Weight Based Feedback Model for Multiple Attributive Group Decision Analysis Problems with Group Consensus Requirements in Evidential Reasoning［J］.European Journal of Operational Research，2011，212（1）：179-189.

［6］李永宾，张凤鸣，李俊涛.基于组合赋权方法的多目标威胁排序［J］.空军工程大学学报（自然科学版），2007，8（2）：7-9.

［7］黄波，顾孟迪，李湛.最佳组合赋权的供应商选择方法及其应用［J］.工业工程与管理，2006，19（5）：14-17，39.

［8］蒋慧峰，朱文杰.一种最优组合赋权算法［J］.湖北工业大学学报，2007，22（5）：78-80.

［9］张国权，李文立，杨件.基于最大离差和最大联合熵的多方案优选方法［J］.运筹与管理，2007，16（4）:12-18.

［10］张国权，李文立，王明征.基于离差函数和联合熵的组合赋权方法［J］.管理学报，2008，3（5）：376-380.

［11］石莉，杨善林，马英，等.一种新的组合权重集结方法及合理性评价研究［J］.系统工程学报，2012，27（8）：481-491.

［12］江亮亮，李雪敏，杨付正，等.引入内容特性分析的包层语音质量评价模型［J］.四川大学学报（工程科学版），2013，45（3）：103-107.

［13］Li Y，McLean D，Bandar Z，et al.Sentence Similarity Based on Semantic Nets and Corpus statistics［J］.IEEE Transactions on Knowledge and Data Engineering，2006，18（8）：1138-1150.

［14］Liu X，Zhou Y，Zheng R.Sentence Similarity Based on Dynamic Time Warping［C］//Proceedings of the 1st IEEE International Conference on Semantic Computing.California，USA，2007：250-256.

［15］乐琦.考虑主体心理行为的双边匹配决策方法［J］.系统工程与电子技术，2013，35（1）:120-125.

［16］秦佳，杨建峰，薛彬，等.基于向量相似度匹配准则的图像配准与拼接［J］.微电子学与计算机，2013，30（6）: 22-25.

［17］Guyon I，Elisseeff A.An Introduction to Variable and Feature Selection［J］.Journal of Machine Learning Research，2003，3（3）：1157-1182.

［18］倪小刚，曹菲.最优权系数组合赋权在导弹质量评估中的应用［J］.长春理工大学学报（自然科学版），2011，34（4）:140-144.

Based on the Pearson Correlation Coefficient of Vector

ZHANG Feng1，XIE Zhen-hua1，CHENG Jiang-tao1，CUI Gao-lun1，XU Heng-bo2
（1.Qingdao Branch of Naval Aeronautical Engineering Academy，Qingdao 266071，China；2.Unit 91033 of PLA，Qingdao 266071，China）

In view of the problem of determining the attribute weight in multi-attribute decision making，this paper establishes a weight computing method considering both subjective and objective weight information based on Pearson Correlation Coefficient（PCC）of vector.PCC of vector is used as the measurement for the importance of the different methods with clear meaning，simple calculation and high operability.Finally，examples show the effectiveness and practicality of this method.

multi-attribute decision making，combination weighting，Pearson Correlation Coefficient（PCC），correlation measure，weight

O159；E92

A

1002-0640（2015）05-0083-04

2014-03-05

2014-04-22

张 峰（1979- ），男，山东淄博人，工程师，博士生。研究方向：多属性决策分析与评估。