某装备系统机电产品贮存可靠性评估方法

罗 赓，穆希辉，杨振海，牛跃听，郭浩亮

（1.军械工程学院，石家庄 050003；2.军械技术研究所，石家庄 050003；3.北京工业大学，北京 100000）

某装备系统机电产品贮存可靠性评估方法

罗 赓1，穆希辉2，杨振海3，牛跃听2，郭浩亮1

（1.军械工程学院，石家庄 050003；2.军械技术研究所，石家庄 050003；3.北京工业大学，北京 100000）

针对某装备系统机电产品长期自然贮存环境下可靠性无法准确评估的难题，提出了一种基于极小χ2估计和拟合优度检验的贮存可靠性评估方法，并对试验数据进行了分析、计算和处理。该方法通过拟合产品的失效分布来确定其分布函数参数，并根据确定的分布函数来预测产品的贮存可靠寿命。与现有的评估方法相比，采用该方法确定的分布函数更能反映产品的可靠性变化规律，对机电产品的贮存寿命预测结果更加合理，在工程研究领域具有很好的实用价值。

可靠性评估，失效分布拟合，拟合优度检验，极小χ2估计，贮存可靠寿命

0 引言

随着科技的发展，装备系统机电产品呈现了高可靠、长寿命、软失效的发展趋势［1］。贮存寿命是该类产品的一项重要技术指标，特别是对于需要长期贮存的产品［2］。

在机电产品的可靠性研究中，产品的失效分布函数的确定是可靠性评估中首要解决的问题。文献［3-8］采用凭借人为经验选择适用的分布类型的方法，该方法的缺点是严重依赖于人的主观判断；文献［9］中提到了矩估计法、图估计法，两种方法计算方便简单，在实践中有普遍的应用。由于矩估计法计算结果的精度与样本数量有很大的关系，当样本数较小时误差较大；图估计法的精度低，且结果易受操作者的主观影响。文献［10］分别运用最小二乘法和极大似然法对3种失效分布进行拟合，结果表明最小二乘法对数据不敏感，极大似然法虽然对数据敏感但存在不利于程序化的问题。

本文首先介绍了长期自然贮存环境下试验数据的特点，针对该特点，提出了一种基于极小χ2估计和拟合优度检验的贮存可靠性评估方法，通过该方法拟合了产品的失效分布，确定了其分布函数参数，最终建立了该机电产品的可靠性数学模型并进行了可靠性评估。

1 试验数据的结构与特点

图1是该机电产品贮存可靠性试验的原始数据结构图。

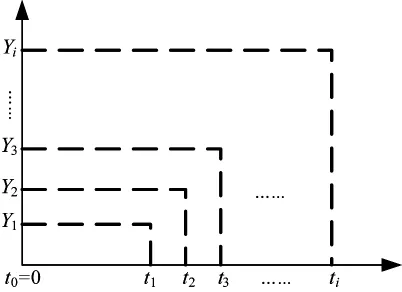
图1 机电产品贮存可靠性数据结构

为了合理地预测产品在自然贮存环境下的贮存寿命，试验数据可采用如下结构，即：

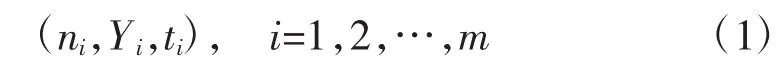
该式表示在从试验开始进行计时到ti时刻对试验产品抽取ni个样本检测，其中有Y个样品经过检测未失效，也就是说该原始试验数据结构可以看成是在ti时刻点由Yi，ti组成的一组变量。

式（1）具有以下4个特点：

（1）成败型数据

该机电产品被认为是不可进行修复的，在检测时，没有失效的数据记为成功，失效的数据记为失败的，因此，试验数据为成败型。

（2）定时试验数据

该机电产品特点为高可靠、长寿命，每件产品的具体失效时间未知，只能将试验时间作为其贮存寿命。

（3）不完全数据

该试验为不完全的截尾试验。通过试验可得到样本中的寿命数据，但其中含有一部分观测中断寿命数据的数据［11］，因而无法获得全样本失效时的贮存时间。获得的试验数据是不完全数据。

（4）数据可能“倒挂”

设产品的贮存寿命为X，则X的失效分布函数为：

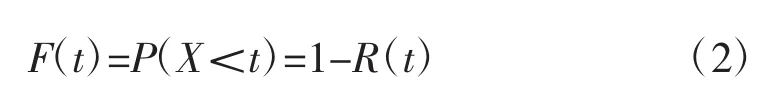
其中，R（t）为贮存可靠度函数。

记时刻ti（格式）的第j个样品的贮存寿命为Xij，i=1，2，…，m；j=1，2，…，ni，Xij独立同分布，其共同的分布函数为F（·；θ），θ=（θ1，θ2，…，θS）'∈Θ⊂RS，θ为参数，Θ为参数空间。

令：

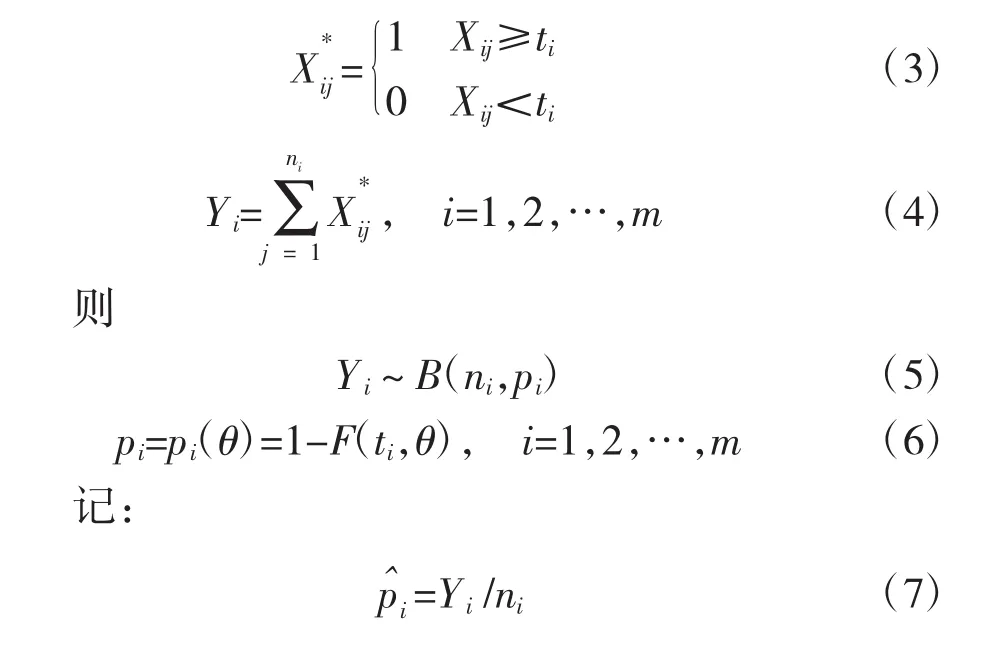
进行试验的产品数据中可能出现一些“倒挂”现象。即贮存时间短的可靠度的点估计值反而比贮存时间长的可靠度的点估计值小，这主要是由于样本的非一致性所致。

对于可能出现的数据“倒挂”问题，采用文献［11］中对“倒挂”数据的处理方法，可以保证可靠度的点估计值随时间的延长而单调递减。

2 分布拟合

2.1 分布类型

假设H0∶F∈，={F（·；θ），θ∈Θ}是分布族，Θ是参数空间。相关的贮存可靠性研究表明，机电产品常见的失效分布族有如下4种：

（1）指数分布族：

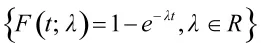
（2）威布尔分布族：

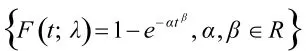
（3）极值分布族：

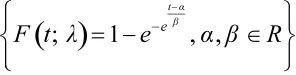
（4）对数正态分布族：

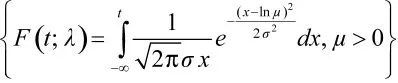
2.2 模型参数确定

令

易见，若真实参数为θ0，当ni→∞，1≤i≤m，χ2（θ0）渐近于自由度为m的χ2分布。若θn满足

具体步骤可分为以下两步：

（1）构造χ2统计量

假定贮存寿命X的分布函数F（t，θ）为某一分布族，基于数据（ni，Yi，ti），1≤i≤m，由式（7）可以得到在ti时刻的i值，再将式（6）与所得i值代入式（8），即可算得χ2统计量表达式。

（2）求出χ2统计量的最小值χ2（n）

对上述χ2统计量关于θ求最小值，得到极小χ2估计n以及极小χ2统计量χ2（θn）。但是此方法只能对产品失效分布作粗略选择，而且不同自由度下的χ2统计量之间也不方便比较。为了解决这个问题，我们在此引出检验的拟合优度。假设上述χ2统量分布符合自由度为m-s的χ2（m-s）分布，其中m为年数，s为参数的个数，则有

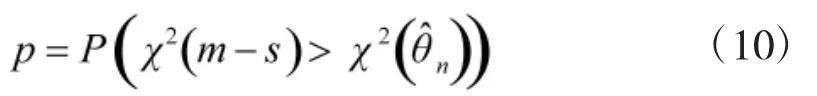
上述p值称为检验的拟合优度，它衡量了假定的分布与数据的拟合程度。一般说来，p值越大，拟合程度越好［12］。

对于贮存可靠性中的4种常见分布族：指数分布族、威布尔分布族、极值分布族和对数正态分布族，可以逐一按上述方法进行检验，从中选择一种最为合适的分布类型。

3 贮存寿命评估与预测

记R（t）为该机电产品的贮存可靠度，RL为给定的可靠度下限，1-α为给定置信度，欲求贮存寿命T，使得P（R（T）≥RL）=1-α，易见

当n→∞时，根据棣莫弗-拉普拉斯中心极限定理得：

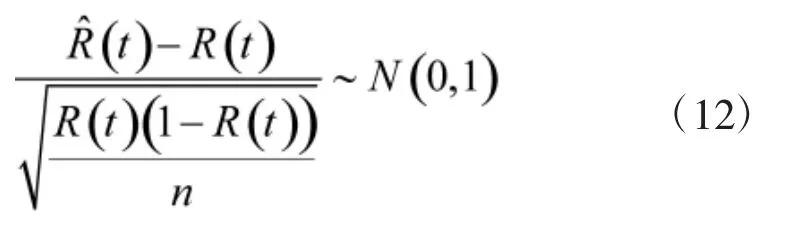
其中，N（0，1）是均值为0，方差为1的标准正态分布。由于满足正态分布，则可以推出

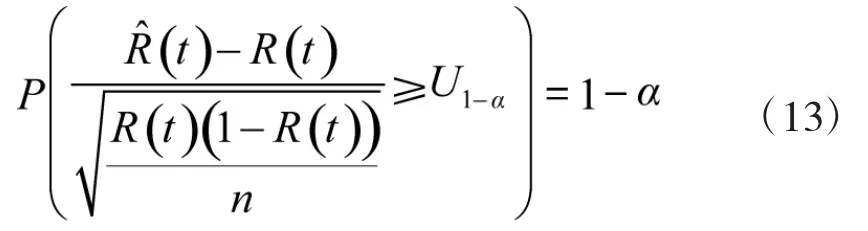
其中，U1-α为标准正态分布的α上分位数，可以从标准正态分布的α分位数表中获得，再通过求解式（13），便可以得到R（t）的下限：

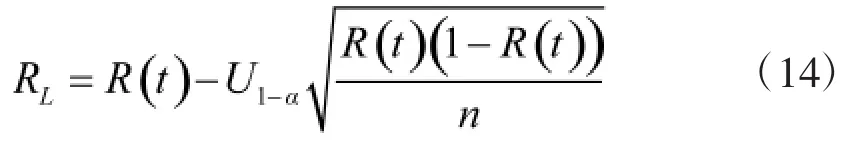
上面的式子中假定ni全相等。但在一些问题中，由于ni不全相等，R（t）的下限可用下式（15）求得［12］：

从式（15）中解出R（t），即可得到所要的T。

4 实例分析

4.1 试验数据

某机电产品做长期自然贮存环境试验，结果如表1所示。试验数据没有“倒挂”，可以对数据不进行预处理。

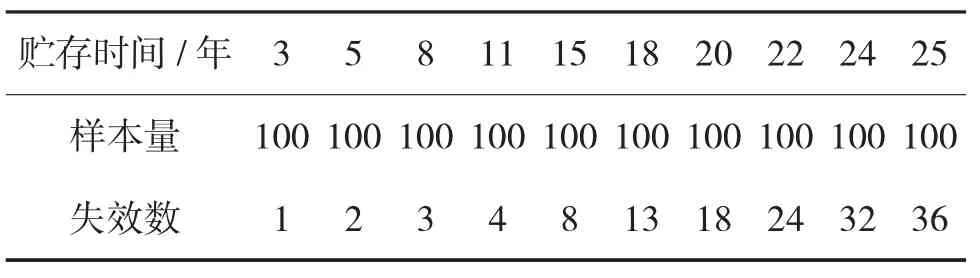
表1 自然贮存环境试验数据

4.2 数据拟合

取0.8为给定的可靠度下限，置信度为0.9。根据表1的试验数据，利用本文提供的方法（方法一），代入公式，可计算出不同分布类型相应的χ2统计量值、拟合优度p值、失效分布函数中的未知参数值以及对应的预测寿命值。

经计算，结果如表2所示。

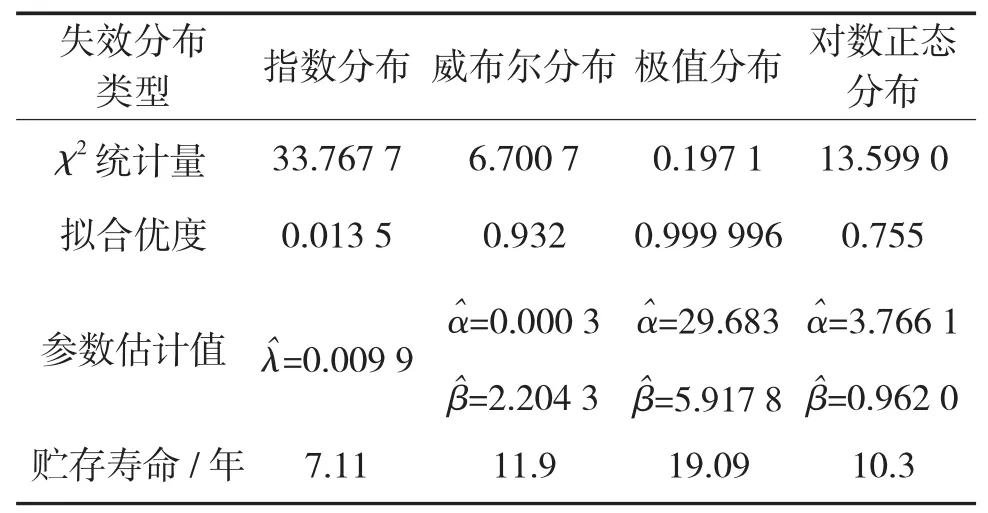
表2 不同分布类型相关计算结果

从表2中可以得知，极值分布的p值最大，拟合效果最好。故该机电产品失效分布函数服从极值分布：

预测贮存寿命为19.09年。

为了进一步检验本文方法正确性与有效性。作出不同分布可靠性分布函数曲线，如图1所图。可以清晰直观地看出极值分布与原始数据之间的拟合程度最好。

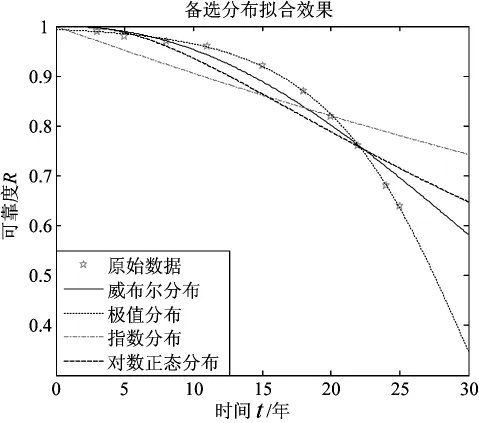
图2 不同分布类型可靠性分布函数曲线

4.3 拟合方法的评判

基于表1的试验数据，采用文献［10］中提到的极大似然估计（方法二），计算得到其失效分布函数也服从极值分布：

预测贮存寿命为18.90年。

下面对本文提出的方法与文献［10］提及的方法进行对比。分别利用确定的分布对各年份的可靠度进行了预测，与检测数据得到的可靠度估计值进行比较，将二者相对误差的标准差作为评判标准。具体步骤如下：

（2）根据已确定分布函数，分别计算通过两种方法得到贮存i年时的可靠度pi（）；

（3）两者的相对误差Ei可通过公式计算得出：

通过上述步骤，得到计算结果见表3。

（4）相对误差标准差估计为：

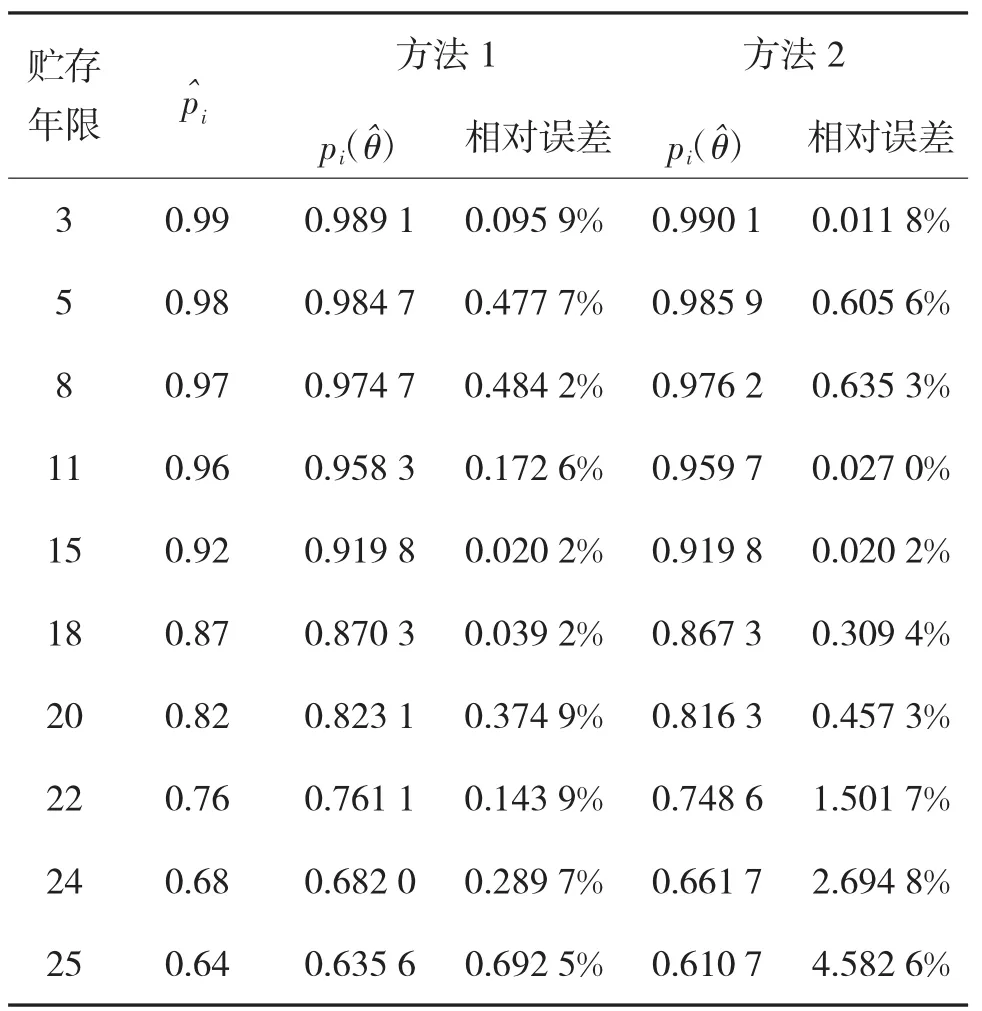
表3 各年份可靠度相对误差表

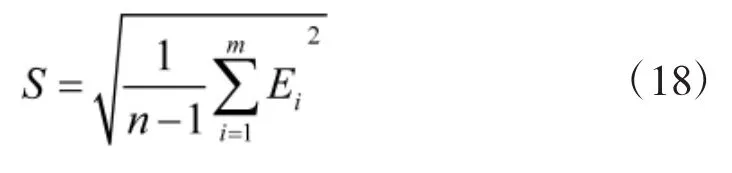
标准差估计S用以作为评价拟合方法优劣的简易标准，S越小，拟合效果越好。

对于方法1，得到S=0.365%。对于方法2，得到S=1.874%。可见方法1得到的S小，可以认为本文提出的方法拟合效果更好。

两种方法的可靠性分布函数曲线如图3所示。可以看到本文的方法不仅在产品贮存的前期拟合效果好，而且在贮存的后期克服了可靠度略显保守的问题，能更准确地拟合产品失效情况。

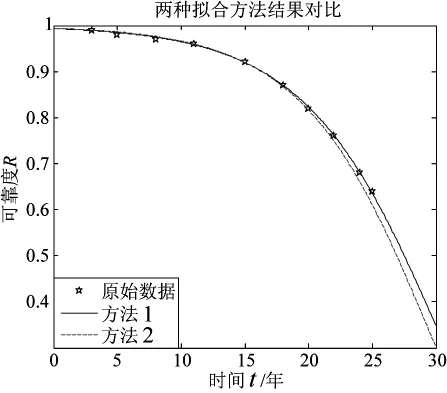
图3 不同拟合方法可靠性分布函数曲线

4.4 结果分析

（1）拟合优度p值越大，备选分布拟合得越准确。

（2）两种方法的计算结果都表明，极值分布为最适合该机电产品的失效分布。

（3）本文的拟合方法与极大似然估计相比，不仅在产品贮存的前期拟合效果好，而且在贮存的后期也能准确地拟合产品失效情况。

（4）达到可靠寿命后，该机电产品的可靠性急骤下降，此时应立刻对其进行维修延寿处理。

5 结论

针对本文试验数据的特点，提出了一种基于极小χ2估计和拟合优度检验的贮存可靠性评估方法，通过该方法拟合了产品的失效分布，确定了其分布函数参数，最终建立了该机电产品的可靠性数学模型并进行了可靠性评估。该方法利于程序化，计算简便，能更加准确地反映可靠性变化规律，使用该方法对机电产品的贮存可靠性进行评估，实际检验表明更加合理、真实。在工程研究领域具有很好的实用价值。

［1］王小林，郭波，程志君.基于维纳过程金属化膜电容器的可靠性评估［J］.火力与指挥控制，2012，37（7）：6-13.

［2］闫楚良，刘克格.飞机结构经济寿命可靠性设计与评定［J］.振动、测试与诊断，2012（3）：355-363.

［3］Chen Z.Component Reliability Analysis of K-out-of-n Systems With Censored Data［J］.Journal of Statistical Planning and Inference，2003，116（1）：305-315.

［4］Whitman C S.Accelerat ed Life Test Calculations Using the Method of Maximum Likelihood：An Improvement Over Least Squares［J］.Microelectronics Reliability，2003，43（6）：859-864.

［5］Sarhan A M.Estimations of Parameters in Pareto Rreliability Model in the Presence of Masked Data［J］.Reliability Engineering and System Safety，2003，82（1）：75-83.

［6］陈文华，崔杰，樊晓燕.单失效数据的可靠性统计分析［J］.机械工程学报，2003，39（9）：44-48.

［7］帅健.腐蚀管线的剩余寿命预测［J］.石油大学学报（自然科学版），2003，27（4）：91-93.

［8］陈云霞，康锐，孙宇锋.导弹飞控系统可靠性仿真研究［J］.航空学报，2004，25（3）：242-247.

［9］龚自立，贾新章，白永亮.元器件质量与可靠性数据统计分布规律的拟合［J］.西安电子科技大学学报，2001（3）：336-339.

［10］祝逢春，王晓鸣，崔大伟，等.航空弹药失效分布拟合方法比较研究［J］.弹箭与制导学报，2006，26（2）：922-925.

［11］祝逢春，崔大伟，刘志扬，等.库存某火工系统贮存寿命评定［J］.火工品，2004（3）：27-32.

［12］杨振海，程维虎，张军舰.拟合优度检验［M］.北京：科学出版社，2011.

［13］熊峻江，武哲，高镇同.不完全疲劳寿命数据可靠性分析的秩统计方法及其应用［J］.航空学报，1998，19（2）：216-219.

［14］刘礼宾，程维虎.阵地弹药贮存可靠性分析及试验数据处理［J］.数理统计与应用概率，1998，13（4）：374-379.

Study on Estimating Method for Storage Eliability of Electromechanical Products in Equipment System

LUO Geng1，MU Xi-hui2，YANG Zhen-hai3，NIU Yue-ting2，GUO Hao-liang1
（1.Ordnance Engineering College，Shijiazhuang 050003，China；
2.Ordnance Technical Research Institure，Shijiazhuang 050003，China；3.Beijing Vniversity of Technology，Beijing 100000，China）

An estimating method based on minimumχ2estimation and goodness fit of test is utilized to evaluate the storage environmental and life of the Electromechanical Products in Equipment System for test date analysis，calculation and processing.Distribution function parameter estimation and reliable storage life prediction are made by using the method.Compared with currently ways，the failure distribution function determined by the method can reflect the reliability of the product more truly.The following result of reliable storage life prediction is reasonable，and this method is promising for engineering application.

reliability evaluation，failure distribution fitting，goodness fit of test，minimum χ2estimation，reliable storage life

TB114.3

A

1002-0640（2015）04-0176-05

2014-01-05

2014-03-07

罗 赓（1990- ），男，陕西咸阳人，硕士研究生。研究方向：机电系统可靠性分析。