随机布阵条件下同时数字多波束干扰优化设计方法

雷 磊，周青松，毛云祥，张剑云

（电子工程学院，合肥 230037）

随机布阵条件下同时数字多波束干扰优化设计方法

雷 磊，周青松，毛云祥，张剑云

（电子工程学院，合肥 230037）

针对现有方法普遍存在的波束形成算法效率低、难以形成多频点多方向的同时多波束干扰、不适用于随机布阵条件下的波束形成等缺点，提出了一种基于二阶锥规划（SOCP，Second-Order Cone Programming）理论的同时数字多波束干扰形成方法。首先，给出了在随机布阵条件下干扰多波束优化设计问题的数学描述；其次，以范数准则为例，将随机布阵条件下干扰多波束设计问题的解析形式转化为相应的SOCP形式；再次，利用现有的原-对偶内点算法工具箱SeDuMi或者CVX进行快速求解。最后，仿真结果表明该方法可以较好地解决随机布阵条件下的多频率多方向雷达目标同时多波束干扰优化设计问题。

随机布阵，二阶锥规划，数字波束形成，同时多波束

0 引言

随着数字多波束形成技术的逐步成熟和广泛应用，数字多波束干扰技术发展迅速。该技术不仅拥有更快、更灵活的波束扫描速度，而且能够通过精确的幅度和相位控制，有效地控制干扰发射波束的旁瓣电平和主瓣宽度，进一步提高有效辐射功率。因此，数字多波束干扰技术必将成为今后电子对抗领域的重要研究课题和发展方向之一。

目前，干扰机的发射阵列天线按照布阵方式大致可分为两类：一类是以均匀线阵、面阵、体阵为主的均匀阵列天线［1］，另一类是按照一定非均匀规律排列的稀布阵列天线［2-3］。二者均对天线阵元的布阵方式提出了一定的要求。然而，在实战应用中，受到时间、地形、人为误差和战场损毁等条件限制，干扰发射天线的阵元间距和相对位置一般很难达到设计的布阵方式要求［4］，如果系统仍按照设定的阵元间距和相对位置计算加权系数，结果就有可能导致主波束偏离设定的方向，因此，研究随机布阵条件下的数字多波束具有很高的实际应用价值。

数字多波束干扰的优化设计本质上属于发射数字波束形成，是将传统相控阵发射波束形成所需的幅度加权和移相从射频部分放到数字部分来实现，从而形成发射波束［5］。之前的学者已对发射波束形成技术作了相关分析研究并提出了一系列的方法［6-11］，这些方法虽然均能满足一定条件下的发射波束形成设计，但主要还是以均匀阵列为研究对象，并且主要还是针对单频点、多方向或者单方向、宽带信号的波束形成问题进行求解，对于随机布阵条件下的数字波束形成，尤其是该条件下的多频点、多方向同时发射多波束形成，其优化设计的复杂程度将远大于之前文献所涉及的波束形成模型，现有文献的方法均难以求解，无法形成有效的多频点、多方向同时多波束干扰。

1 问题描述

均匀布阵的N1元面阵如图1所示，随机布阵的N1元面阵如图2所示。二者的所有阵元都分布在一个边长为·d的正方形平面区域内，区别在于前者相邻阵元的间距严格为d，而后者的所有阵元均在规定区域内随机布置。

假设干扰多波束由一个如图2所示的随机布阵的面阵产生，其阵元数为N1，将所有阵元由0至N1-1进行编号。不妨设0号阵元为基准阵元，其平面直角坐标记为（x0，y0），则m号阵元的平面直角坐标可记为（xm，ym）；再将每个阵元的信号分别进行（N2-1）级延时，并取每个阵元的抽头数为N2，其中未经延时的信号抽头（基准抽头）记为该阵元的0号抽头，经n级延时的信号抽头记为该阵元的n号抽头。则各个阵元中各个抽头的加权系数可记为W={wmn∈R，0≤m≤N1，0≤n≤N2-1}，W∈RN1×N2，其中m，n分别表示阵元序号和延时级数。

图1 均匀布阵的N1元面阵示意图

图2 随机布阵的N1元面阵示意图

经（N2-1）级延时的N1元阵列如图3所示。中频信号经分路器分别进入N1个阵元所对应的延时支路，经延时叠加，再经D/A转换，进入混频器与频率为fL的本振信号进行混频，将原中频信号上变频到射频，最后分别由N1个阵元发射到空间中，形成多频点、多方向的同时干扰多波束。

进而该干扰发射波束形成模型在中频段可以写为：

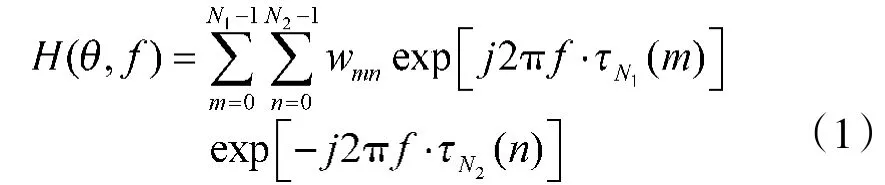
图3 经（N2-1）级延时的N1元阵列示意图

其中，θ为信号方向与阵列法线间的夹角（方位角），并且θ∈Θ，Θ代表感兴趣的方位角度范围；f为射频干扰信号经下变频后在中频段所对应的频率，并且f∈Ω，Ω代表感兴趣的中频频率范围。表示号阵元与0号阵元之间由于阵元间距及相对位置差异而在中频段产生的延时，表示n号抽头相对于0号抽头的延时，二者的表达式分别为：

式中，（xm，ym）为m号阵元的平面直角坐标，c为光速，s为每级延时的时间间隔，fs为信号采样频率（这里令）。

将式（2）、式（3）代入式（1），可得：

对于压制式干扰的波束优化设计，其基本设计思路是在干扰总功率和波束主瓣宽度一定的情况下，对准敌方探测信号的频率和方向形成干扰波束，并约束波束的旁瓣电平（功率），使干扰功率尽可能地集中在波束的主瓣方向。

现假设有I个频率和方向均不相同的单频点雷达探测信号，要求设计一个多频点、多方向的干扰波束对其进行瞄准式干扰。可将干扰总功率I等分，使分配到每个目标频点上的干扰功率归一化值均等于1，相当于附加I个等式约束，从而将干扰多波束优化设计问题表述为：

θql，θqp分别表示第q个目标频点上的波束旁瓣方位角和波束主瓣方位角，fq表示第q个目标频点的频率值；Θlq，Θpq，Θ分别表示第q个目标频点上的波束旁瓣方位角范围、波束主瓣方位角范围和感兴趣的总体方位角范围（注意，对于含有上标或下标的字母，例如Θlq，仅根据下标q对其进行索引，而不根据上标进行索引，下文中类似），L，P，M1则分别表示3个方位角范围内的离散化栅格点数；Ωq，Ω分别表示波束所在的目标频点的频率范围和感兴趣的总体频率范围，Q，M2则分别表示两个频率范围内的离散化栅格点数。因为所有目标信号均为单频点信号，所以目标信号的个数即为目标频点频率范围内的离散化栅格点数，即I=Q。

这里应注意：因为干扰多波束的形成实质上属于发射多波束形成，因此，可以利用前期侦查所得的先验知识信息，确定需要形成干扰波束的多个目标频点和对应的目标方向，然后同时在这多个目标频点上对波束的旁瓣进行Lk范数准则约束，对波束的主瓣进行等式约束。对于非目标频点的频率范围，即（Ω-Ωq），则认为对该范围内的所有频点并不分配干扰功率，因此，不会形成干扰波束，从而大大降低了优化过程中的运算量。

对于问题（5），k的取值代表不同的范数准则，通常k取1，2或者∞，它们分别代表干扰多波束优化设计常用的L1范数，L2范数和L∞范数准则。即：

在干扰多波束优化设计中，当单一范数准则不能满足实际应用要求时，可以通过另外附加某种范数约束实现混合范数优化，从而将干扰多波束设计问题表述为：

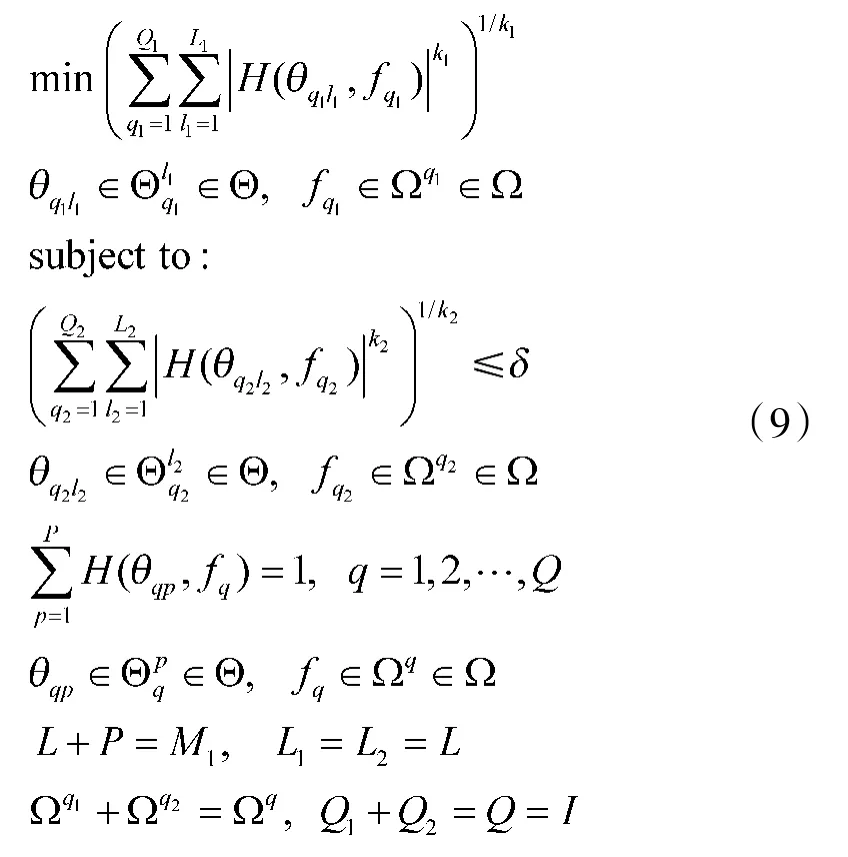
其中k1，k2取1，2或者∞，δ表示某种范数的上界。

综上所述，干扰多波束的优化设计问题可以由式（9）所给出的形式统一表述，因此，干扰多波束优化设计的关键在于如何快速求解优化问题（9）。

2 问题的SOCP形式

由矩阵理论可知，当k≥1时，任何k-范数球都是凸的，因此，问题（6）～问题（9）都是典型的凸优化问题，可以方便地转化为SOCP问题进行求解。本节将给出问题（7）的L2范数准则条件下干扰多波束优化设计的SOCP形式。

取k=2，即对多个目标频点上的波束旁瓣进行L2范数准则约束，对波束主瓣进行等式约束。引入辅助变量ξ，则问题（7）与下述问题等价：

并且当k=1时，定义一维二阶锥为cone1={t|t∈R，0≤t}。

现对旁瓣功率约束的L2范数误差进行展开可以得到：

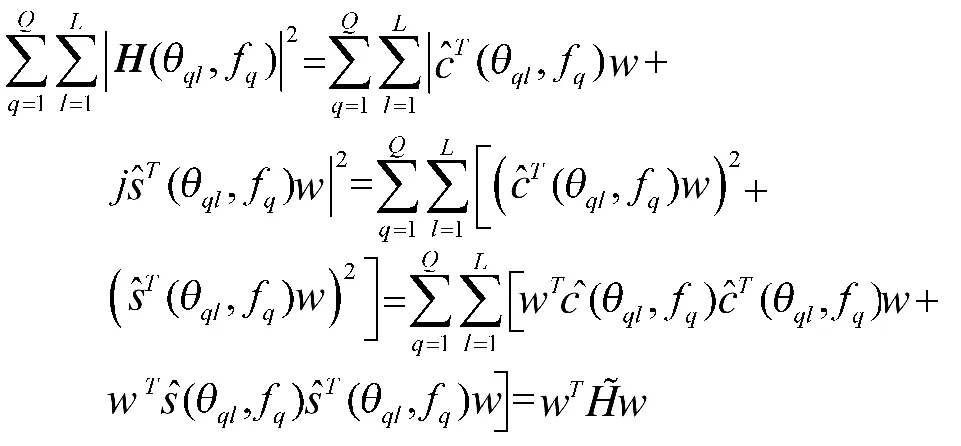
同理，将主瓣功率的约束条件也写成SOCP形式：

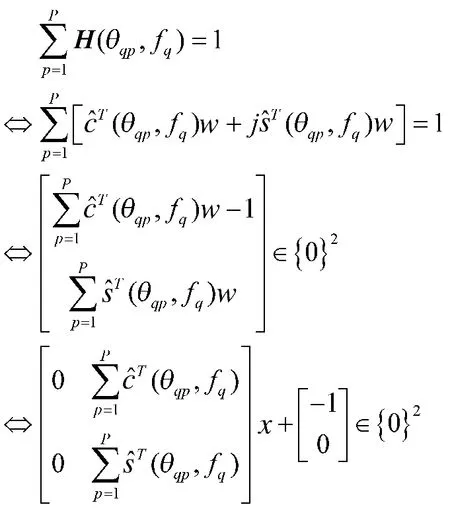
因此，问题（11）的SOCP形式为：

对于其他准则约束条件下的设计问题，其SOCP形式的数学推证过程与以上类似，这里省略。

3 仿真分析

设计要求：假设现有3个频率和方向均不相同的单频点雷达探测信号，它们的来波方位角分别为θ1=40°，θ2=90°，θ3=140°，射频频率分别为f1'=2 GHz，f2'=1.9 GHz，f3'=2.1 GHz，经本振频率为fL=1.8 GHz的变频器进行下变频处理，搬移到中频进行处理时，对应的中频频率分别为f1=200 MHz，f2=100 MHz，f3= 300 MHz，要求设计一个多频点、多方向的干扰波束对上述多部雷达进行同时干扰。

设计准则：L2范数准则。

仿真参数：设定感兴趣的总体方位角范围为Θ=［0°，180°］，其中的方位角离散化栅格为180，即方位角离散化栅格点数M1=181；设定感兴趣的中频段频率范围为Ω=［0，400 MHz］，其中的频率离散化栅格为100，即频率离散化栅格点数M1=101；分别用三组不同的36元阵列天线形成发射波束，即N1=36，其中第1组为一个均匀布阵的36元面阵，另外两组为两个随机布阵的36元面阵；每个阵元的信号分别进行二级延时，即各阵元的抽头数N2=3；信号处理的带宽B=maxΩ=400 MHz，采样频率fs=800 MHz，光速c=3×108m/s，阵元间隔d=0.5=0.5；若将主瓣零点波束宽度的预先约束设定为θm=20°，则波束主瓣方位角范围］=［θq-10°，θq+10°］，离散化后的θqp=θq-10°，θq-9°，…，θq+10°，离散化栅格点数P=21；同理，波束旁瓣方位角范围Θql=［0，θq-10°）∪（θq+10°，180°］，离散化后的θql=0，1°，…，θq-11°，θq+11°，θq+12°，…，180°，离散化栅格点数L=160；目标频点的频率范围Ωq={fq|q=1，2，…，Q}，Q=I=3。

仿真环境：Intel（R）Core（TM）i3 CPU 550@ 3.20 GHz。

设计结果：均匀布阵的36元面阵阵元位置坐标如图4所示，其同时数字多波束干扰的波束形成效果如图5所示，波束性能指标如表1所示。

图4 均匀布阵的36元面阵阵元位置坐标图

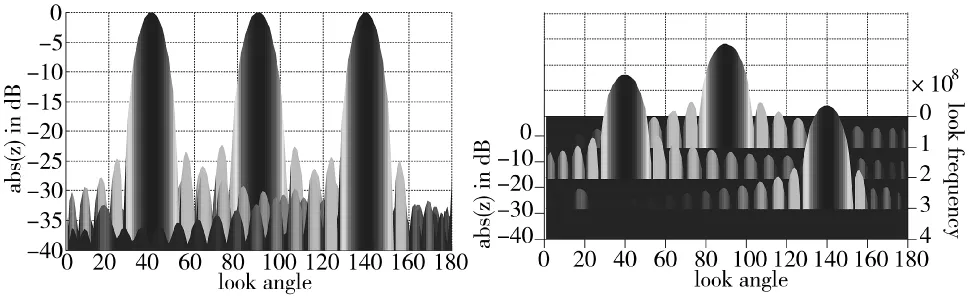
图5 同时数字多波束干扰的波束形成效果图（均匀布阵）

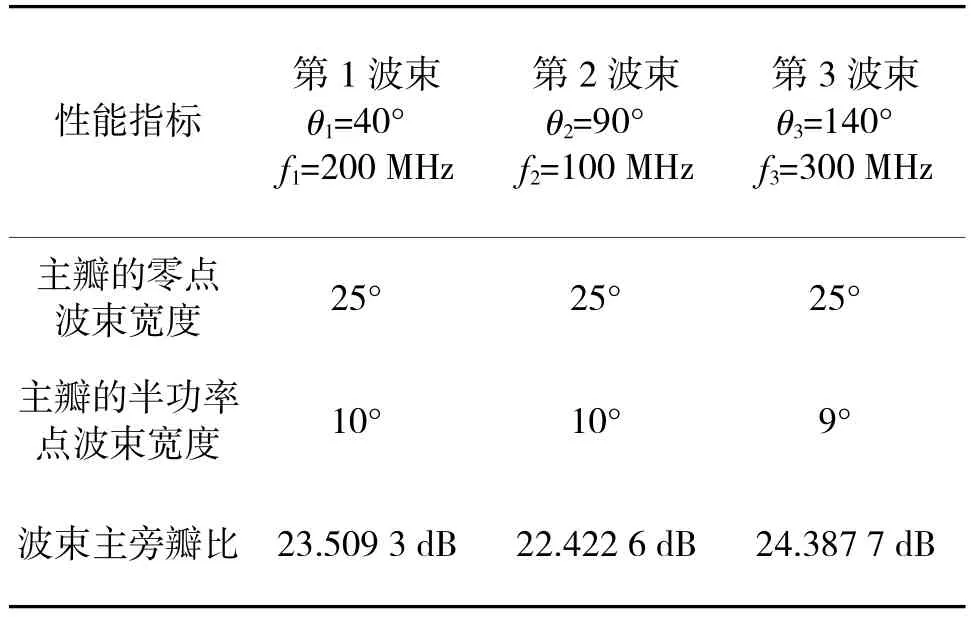
表1 L2范数准则下的干扰多波束性能指标（均匀布阵）

第1组随机布阵的36元面阵阵元位置坐标其同时数字多波束干扰的波束形成效果如下页图6、图7所示，波束性能指标如表2所示。

第2组随机布阵的36元面阵阵元位置坐标，其同时数字多波束干扰的波束形成效果如下页图8、图9所示，波束性能指标如表3所示。

图6 第1组随机布阵的36元面阵阵元位置坐标图

图7 同时数字多波束干扰的波束形成效果图（第1组随机布阵）

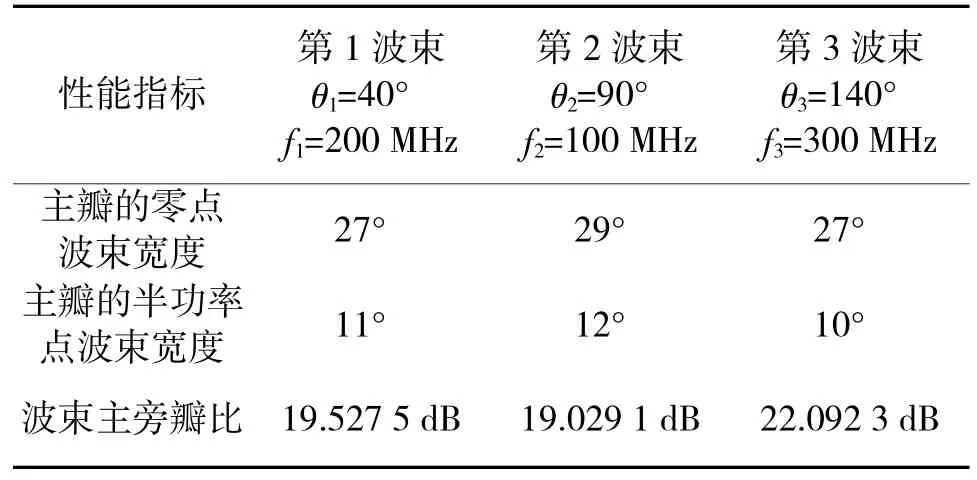
表2 L2范数准则下的干扰多波束性能指标（第1组随机布阵）

图8 第2组随机布阵的36元面阵阵元位置坐标图

图9 同时数字多波束干扰的波束形成效果图（第2组随机布阵）

表3 L2范数准则下的干扰多波束性能指标（第2组随机布阵）

结果分析：比较表1～表3可知，第2组随机布阵时的干扰多波束性能指标总体优于均匀布阵时的干扰多波束性能指标，而均匀布阵时的性能指标总体优于第1组随机布阵时的性能指标，这是因为阵列中各个阵元的随机布置导致延时精确补偿的难度较均匀布阵有了一定的改变。根据大量实验表明，在其他条件相同的情况下，均匀布阵方式往往并不是阵列中阵元布置的最佳方式，因此，必然存在部分非均匀的布阵方式，使得该同时数字多波束干扰优化设计的波束形成效果优于均匀布阵。同时，部分非均匀的布阵方式也可能使得波束形成的效果变差。在算法优化求解能力一定的情况下，若其波束性能指标优于均匀布阵，则说明该次随机布阵的结果使得延时精确补偿的难度降低，波束形成效果得到了一定的改善；若其波束性能指标劣于均匀布阵，则说明该次随机布阵的结果使得延时精确补偿的难度升高，波束形成效果有所下降。此外，该结果还可以说明，在其他条件相同的情况下，必然存在一组阵元位置的最优布置方案，使得该同时数字多波束干扰优化设计的波束形成效果最佳。如何寻找这一最优配置方案也将成为下一步的重点研究内容之一。

同时，还可以发现，在3组仿真参数设定时，均期望将主瓣的零点波束宽度分别约束在20°左右，但实际仿真效果往往略大于预设值，这是因为在波束优化设计问题中，旁瓣功率和主瓣宽度是一对矛盾的设计指标，特别是对于多频点、多方向的波束优化设计，约束旁瓣功率往往会导致主瓣宽度的展宽。对于干扰波束形成来说，较宽的波束主瓣宽度必然会带来一定的功率浪费，但在干扰功率允许的情况下，宽波束较窄波束也存在一定的优势：当干扰目标在做高速度或大角度机动时，宽波束可以使目标不易逃脱干扰波束的空域覆盖范围，也就是降低了对干扰波束指向变化灵活性的要求，从而进一步保证了干扰的总体效益。

综上所述，由主瓣零点波束宽度、主瓣半功率点波束宽度和波束主旁瓣比3个指标可知：虽然随机布阵下的波束形成设计结果较均匀布阵时有一定的波动，但总体的设计结果基本满足了期望实现的干扰多波束覆盖空域范围、干扰功率有效利用率和主旁瓣功率比等性能指标，达到了优化设计的预期要求。

4 结束语

本文提出了一种基于SOCP的干扰多波束优化设计方法，成功解决了随机布阵条件下，“一部干扰机同时干扰多部雷达”技术中的同时多波束形成问题。首先给出了在随机布阵条件下干扰多波束优化设计问题的数学描述，其次以范数准则为例将随机布阵条件下干扰多波束设计问题的解析形式转化为相应的SOCP形式，然后可以利用现有的原-对偶内点算法工具箱SeDuMi或者CVX进行求解。最后通过仿真表明，该方法为随机布阵条件下的数字干扰多波束设计提供了一种思路，在实际应用过程中还可以采用混合范数方法，将多个约束条件纳入到单个优化问题当中，进而达到兼顾干扰多波束各个设计指标的目的，应用十分灵活和方便。

［1］李颖.均匀圆阵列天线系统性能分析［D］.长沙：国防科学技术大学，2004.

［2］陈客松.稀布天线阵列的优化布阵技术研究［D］.西安：电子科技大学，2006.

［3］曹运合，王胜华，张守宏，等.宽带稀布阵列发射波束形成技术［J］.系统工程与电子技术，2005，27（4）：600-602.

［4］王 江，宋铮.最大信干噪比准则下智能天线随机布阵效果研究［J］.舰船电子工程，2004，24（2）：84-86.

［5］张明友，汪学刚.雷达系统［M］.北京：电子工业出版社，2009.

［6］Patton L K，Rigling B D.Modulus Constraints in Adaptive Radar Waveform Design［C］//IEEE Radar Conference，Rome，Italy，2008.

［7］Fuhrmann D R，Antonio G S.Transmit Beamforming for MIMO Radar Systems Using Signal Correlation［J］.IEEE Transactions on Aerospace and Electronic Systems，2008，44（1）：1-16.

［8］ Stoica P，Li J，Zhu X.Waveform Synthesis for Diversity-based Transmit Beampattern Design［J］.IEEE Transactions on Signal Processing，2008，56（6）：2593-2598.

［9］Guo B，Li J.Waveform Diversity Based Ultrasound System for Hyperthermia Treatment of Breast Cancer［J］.IEEE Transactions on Biomedical Engineering，2008，55（2）：822-826.

［10］胡梦中，宋铮，刘月平.一种新的低副瓣多波束形成方法［J］.现代雷达，2007，29（10）：71-74.

［11］罗仕红.MIMO雷达波形设计与波束形成研究［D］.合肥：电子工程学院，2011.

Optimal Design Method of Synchronous Digital Multiple Beamforming for Jamming in Condition of Stochastic Embattling

LEI Lei，ZHOU Qing-song，MAO Yun-xiang，ZHANG Jian-yun
（Electronic Engineering Institution，Hefei 230037，China）

The present beamforming methods for radar jamming are subject to many flaws such as low efficiency，difficulty to form synchronous multi-beam jamming，inapplicability to stochastic embattling.In this paper，a new beamforming method based on SOCP is proposed for the synchronous multi-beam radar jamming.First，the optimal design problems in the condition of stochastic embattling can be formulated into the mathematical description under different norm criteria.Then，translate the mathematical description of synchronous multiple beamforming for jamming in the condition of stochastic embattling into a SOCP form under the norm criteria.Moreover，this SOCP problem can be solved effectively via CVX or SeDuMi.Last，the related constraints simulation results show that the approach can solve the design problem efficiently.

stochastic embattling，second-order cone programming，digital beamforming，synchronous multi-beam

TN974

A

1002-0640（2015）06-0119-06

2014-05-11

2014-06-20

雷 磊（1990- ），男，硕士研究生。研究方向：雷达对抗。