铝合金夹心板甲板结构荷载横向分布作用及其试验研究

冯安涛，周新刚

(烟台大学土木工程学院，山东烟台264005)

铝合金夹心板甲板结构荷载横向分布作用及其试验研究

冯安涛，周新刚

(烟台大学土木工程学院，山东烟台264005)

根据铰接板理论，分析了横向荷载作用下，铝合金甲板结构中铝合金夹心板的互相作用及其荷载分布，并与试验结果进行了对比分析.理论和试验研究表明，铝合金夹心板拼接形成的甲板结构，在横向荷载作用下具有明显的相互作用.分析计算甲板的受力性能时考虑横向荷载分布的影响，能比较好地反映甲板的整体受力性能，对甲板的优化设计具有重要的作用.

铝合金夹心板;载荷试验;横向分布系数;铰接板理论

铝合金材料具有强度高、密度小、耐腐蚀的特点，且具有良好的加工性能，通过挤压成型等方式可以加工成任意形状的铝合金型材［1-3］.在挤压加工过程中，材料的力学性能不会发生改变.铝合金的应用非常广泛，传统上主要应用在航空等领域，目前在海洋工程、军事工程以及民用大跨度结构等中也有广泛的应用［4-5］.作为结构材料，铝合金型材主要分为2类，一类是作为主要受力构件的H型、槽型、L型及管型(方形或圆形)构件(图1)，一类是各种形状的夹心板构件(图2).夹心板构件通过拼装组成的甲板结构可以作为墙面或屋面覆盖结构，也可以作为舟桥的甲板及海洋平台停机坪的甲板等.

图1 铝合金型材Fig.1 Aluminum alloy profiles

图2 铝合金夹心板Fig.2 Aluminum alloy sandwich plate

铝合金夹心板甲板结构是通过夹心板边缘的齿槽拼接而成(图3)，当板上作用的竖向荷载非均匀分布时，板与板之间存在相互作用，即一块板上的荷载通过齿槽之间的连接向其他板上传递.这种相互作用，在桥梁结构中又称为荷载的横向分布作用.根据荷载横向分布理论，荷载横向作用的大小与板之间的横向连接刚度及夹心板本身的抗弯、抗扭刚度有关［6］.本文根据铝合金夹心板拼接形成的甲板结构的特点，采用铰接板理论分析了铝合金夹心板的荷载横向分布作用，并根据试验结果进行了分析验证.理论和试验研究表明，采用铰接板理论分析不带横向连接的铝合金夹心板甲板结构，可以很好地揭示夹心板甲板结构的受力特点，对夹心板甲板结构的优化设计具有重要意义.

图3 齿槽连接构造Fig.3 Slotted connection structure

1 铝合金夹心板甲板荷载横向作用分析

根据荷载横向分布理论，荷载横向分布的计算分析方法主要有:杠杆原理法、偏心压力法、横向铰接板法、横向刚接板法和比拟正交异性板法等［7］.对于仅在翼板间采用焊接连接或直接交叉连接的中间无横隔梁的装配式板，虽然板块间有一定的连接构造，但其连接刚度相对较为薄弱，这类结构的受力状态接近于数根并列、相互间横向铰接的狭长板.这种情况一般采用铰接板理论分析计算荷载横向分布作用［6-8］.根据图3铝合金夹心板拼装组成的甲板结构中铝合金夹心板之间的连接特点，铝合金夹心板甲板结构符合铰接板理论的分析条件.

1.1 荷载横向作用分析基本方程

根据铰接板理论的基本假定，在竖向荷载作用下，接缝只传递竖向剪力.采用半波正弦荷载分析跨中荷载横向分布的规律，其荷载表达式为

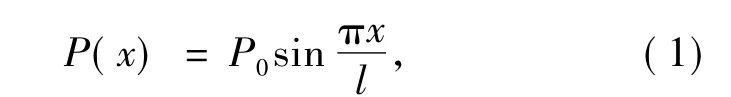
夹心板的拼接构造可简化为图4所示的模型，按铰接板理论，在半波正弦荷载作用下，任意板间的铰接缝上承受的荷载也为半波正弦荷载(图5).

图4 夹心板连接结构Fig.4 Connection structure of sandwich plate

当任意板i上作用单位正弦分布荷载时，板与板之间相互作用的分析简图如图6所示(P=1).荷载以剪力的形式通过铰接缝传递.将甲板结构沿着铰接缝切开，则每一个铰接缝内均作用着一对大小相等、方向相反的正弦分布铰接力.对于n块夹心板拼接而成的甲板结构，具有(n-1)条铰接缝，则有(n-1)个未知铰接力峰值gj需要求解.

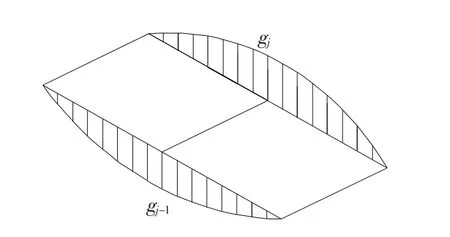
图5 铰接板铰接缝的受力分布Fig.5 Force distribution of the hinged plate hinge joint

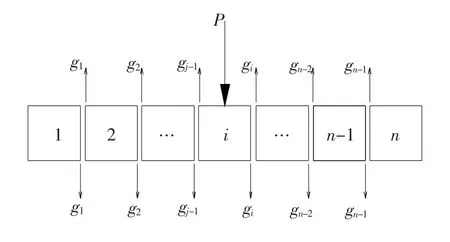
图6 单位荷载作用于第i跨时的计算模型图Fig.6 Calculation model when the unit load applied on the ith span

对于单块夹心板取隔离体，由于每块板两侧接缝的剪力大小不同，板既受到横向荷载作用，又受到由此产生的扭矩作用.可以用作用在夹心板上的中心荷载及其扭矩代替.因此，如图7所示，可以用横向力gi和mi作为基本未知力;竖向位移ω和φ作为对应的位移.

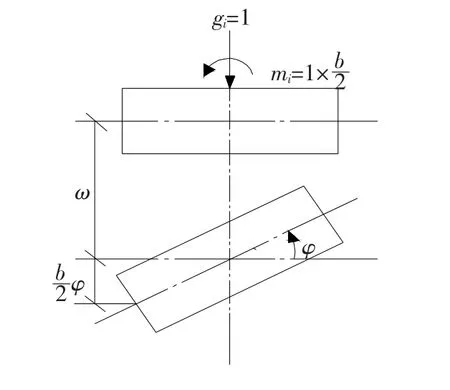
图7 板的受力分析图Fig.7 Force analysis for plate

将(n-1)条铰接缝切开形成基本体系，利用2相邻板块在铰接缝处竖向位移的变形协调条件，通过力法原理求解各夹心板的铰接力峰值.对于图6的各夹心板甲板结构的基本体系，可以列出正则方程如下［7］:

随着传统文化的存在变得越来越艰难，人们似乎也渐渐师徒做一些努力来挽回，这其中，景观设计中越来越多的传统文化的运用便是很好的例子，很多地方的景观建筑都开始走复古风格，像传统靠拢，这确实是令人振奋的现象。下面就来为大家具体列举一些传统文化在景观设计当中的应用：

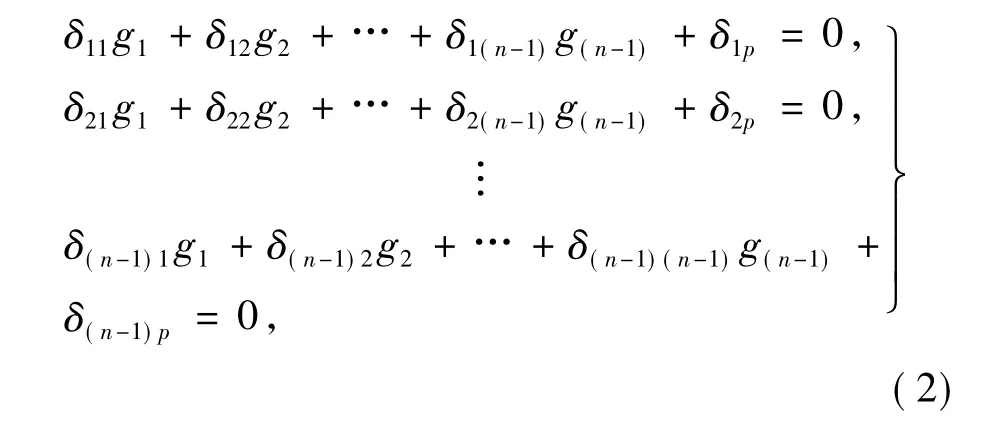
式中:δjk为铰接缝k内作用单位正弦铰接力时，在铰接缝j处引起的竖向相对位移;δjp为外荷载p在铰接缝j处引起的竖向位移．

式中:ω为第i板的位移;φ为第i板的转角．式中δip=-ω，其他常系数均为0．将系数带入正则方程(2)，令γ=bφ/2并化简，得解析式［6］:

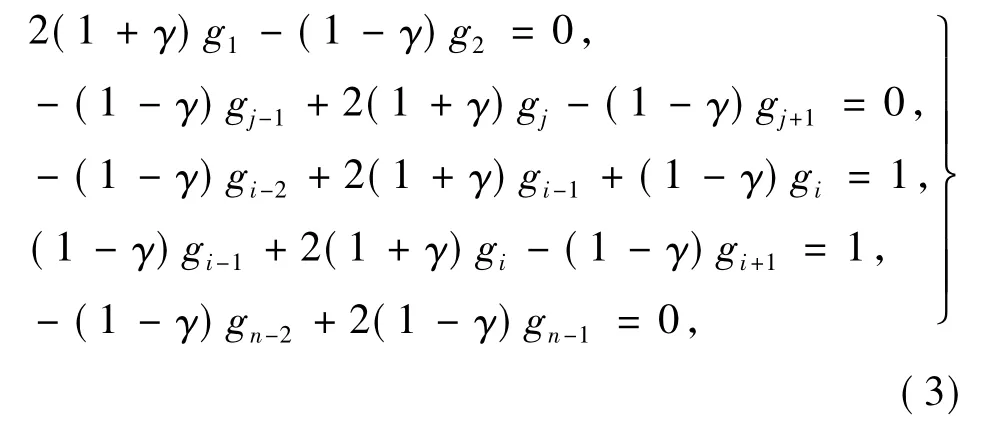
其中:2≤j≤n-2，且j≠i-1，j≠i．

对于简支铰接夹心板，将ηij定义为第i块板上作用荷载P时横向分布给第j块板的荷载分布系数，即各板中点的荷载横向影响线系数，就可以按单梁理论分析单个拼接板的内力和变形了．

由图6分析可知，每块夹心板中点的荷载横向影响线系数为

式中:gj为第j条铰接缝的铰接力．

由式(3)可知，确定了刚度参数γ、板块数量n和荷载的作用位置，即可求得(n-1)个未知铰接力的峰值gj和各板中点的荷载横向影响系数ηij．

1.2 参数的确定

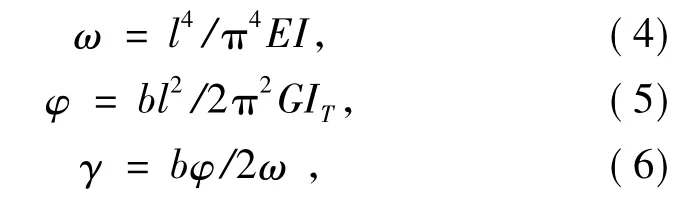
式中:l为夹心板跨度;E、G分别为夹心板材料的弹性模量和剪切模量;I、IT分别为夹心板截面的抗弯惯性矩和抗扭惯性矩．

图8所示的典型夹心板截面的截面特性参数计算如下:截面抗弯惯性矩为

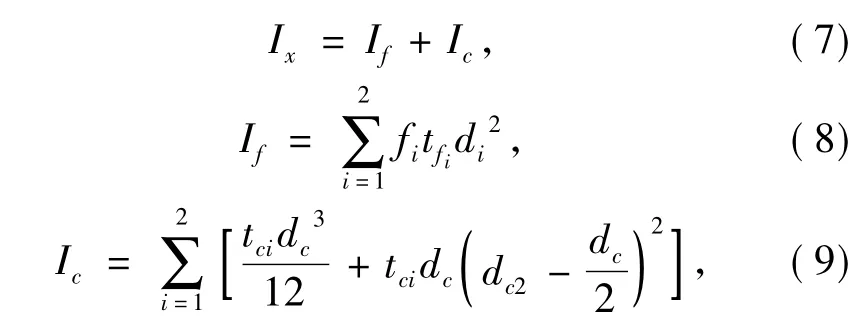
式中:Ic、If分别为夹心板截面的夹心部分抗弯惯性矩和翼缘部分抗弯惯性矩.

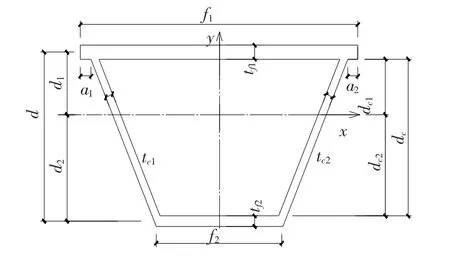
图8 典型夹心板截面Fig.8 A typical sandwich board section

截面的抗扭惯性矩为［7］

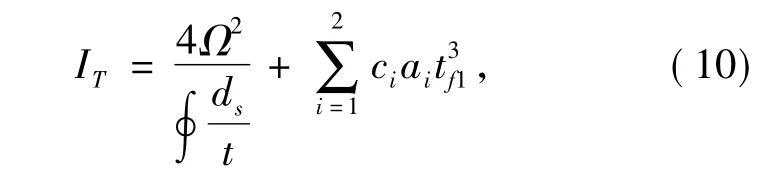
式中:Ω为夹心板外围薄壁中线所围的面积;ci为矩形截面抗扭刚度系数，按表1确定［7］.

表1 矩形截面抗扭刚度系数取值Tab.1 Values of rectangular section torsional stiffness coefficient

简支板挠度计算:

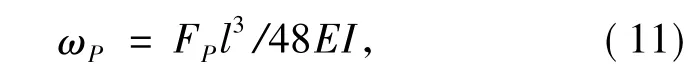
式中:FP为板跨中承担的荷载.

2 试验研究

文中选择如图9所示的铝合金夹心板组成的甲板进行试验研究.根据公式(4)～(6)及图9所示的夹心板截面尺寸，计算的参数见表2.

根据前述的横向荷载分布的铰接板理论计算分析，当荷载作用在中间板的跨中时，计算得到的荷载横向分布系数影响线见图10所示.

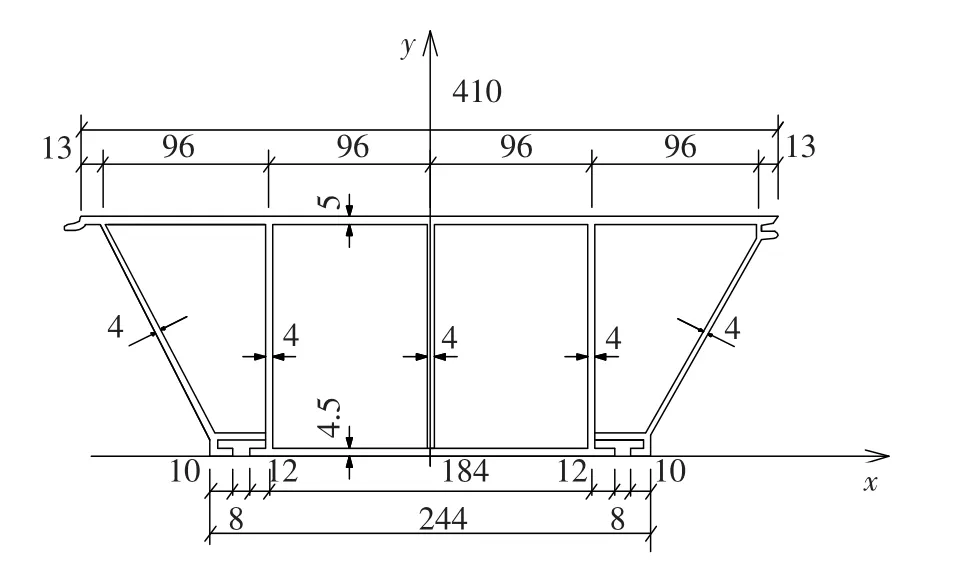
图9 截面尺寸(mm)Fig.9 Sectional dimension

表2 铝合金夹心板的截面特性参数及分析参数Tab.2 Cross section parameters and the analysis parameters of aluminum alloy sandwich panel

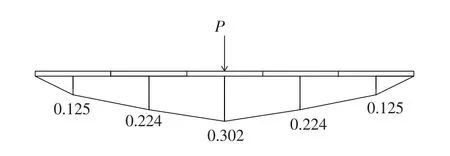
图10 荷载横向分布系数影响线Fig.1 0Influence line of the load transverse distribution coefficient

计算结果表明，图9所示截面形式的夹心板结构拼接组成的甲板具有较好的荷载横向传递能力，各拼接板之间共同作用承担上部施加的荷载.5块拼接板共同承受荷载作用时，直接承受荷载的夹心板较单独承受荷载时所分担的荷载降低了近70%，所以，该铝合金夹心板结构及其连接构造具有良好的荷载横向传递能力，铝合金夹心板甲板结构有较强的整体受力性能.

为验证铰接板理论分析夹心板甲板结构荷载的横向分布的适用性，对图11所示的甲板进行试验.甲板为简支，在中间板的跨中施加集中荷载.根据CAP437船载直升机规范［9］，荷载分别施加107 kN和179 kN，模拟EH101型直升机平稳着陆时和紧急着陆时对甲板产生的竖向荷载.

在不同荷载水平下，各块板实测的挠度及按照铰接板理论计算的挠度见图12.从计算及试验结果看，计算结果与试验值吻合良好.说明前述的铰接板理论可以很好地分析铝合金夹心板组成的甲板结构在横向荷载作用下的相互作用.通过比较考虑夹心板的相互作用时直接承受荷载的夹心板的挠度与不考虑相互作用时单块夹心板的挠度数据(表3)，结果表明，考虑夹心板的相互作用可以显著降低局部集中荷载作用下板的变形.因此，在甲板结构设计中，考虑夹心板的相互作用，可以对甲板结构进行优化设计.

图11 试件加载位置图(mm)Fig.1 1Position of the load applied on the specimen

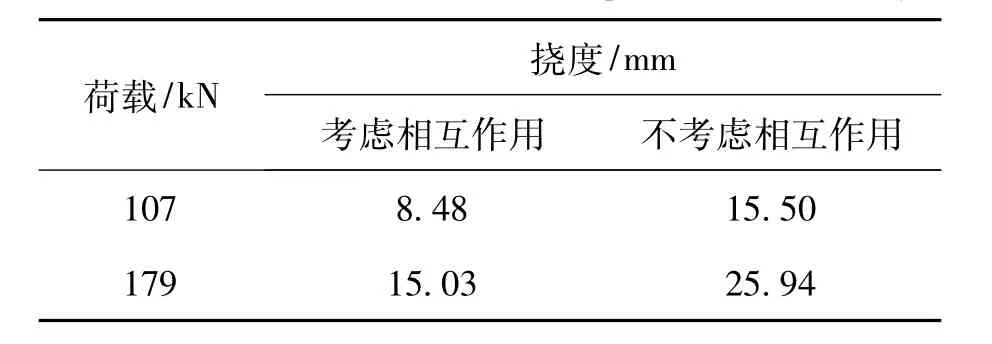
表3 直接承受荷载的夹心板的挠度Tab.3 The deflection of sandwich panel loaded directly

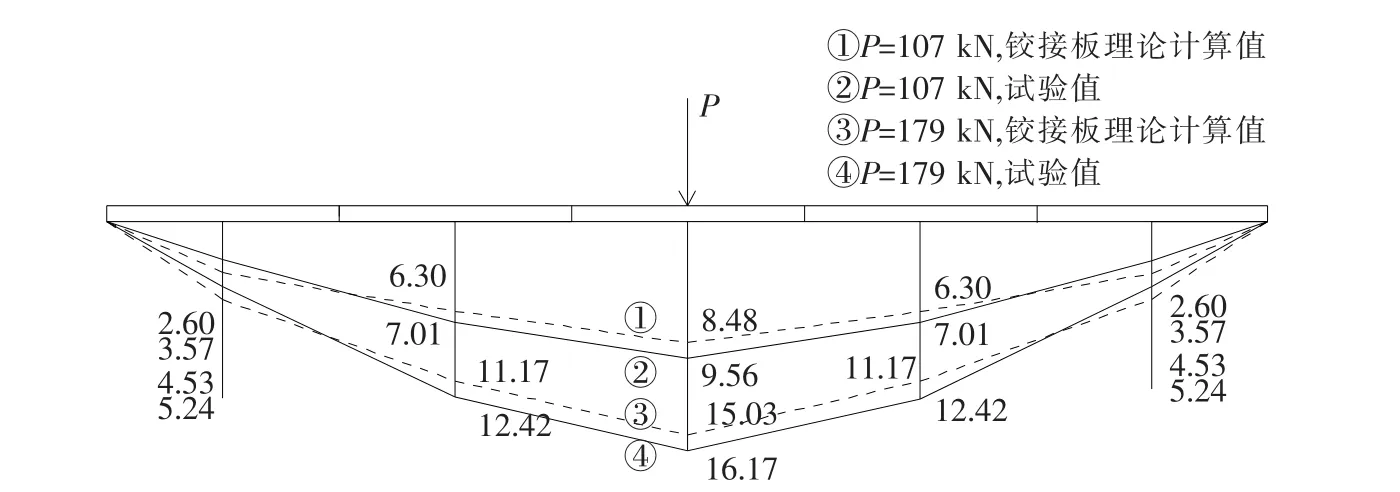
图12 理论计算和试验测试挠度比较(mm)Fig.1 2Comparison of theoretical calculation and experimental test deflection value

3 结论

本文通过铰接板理论，分析了横向荷载作用下，铝合金夹心板甲板结构中铝合金夹心板的互相作用及其荷载横向分布，并进行了铝合金夹心板甲板载荷试验.理论和试验研结果对比分析表明，铝合金夹心板拼接形成的甲板结构，在横向荷载作用下具有明显的相互作用，夹心板之间的相互作用可以显著降低局部集中荷载作用下板的变形.考虑横向荷载分布的影响，分析计算甲板的受力性能，可以很好地揭示夹心板甲板结构的受力特点，并且能较好的反映甲板的整体受力性能，对甲板的优化设计具有重要的作用.

［1］Dwight J.Aluminum design and construction［M］.London:Spon Press，1999:1-14.

［2］钱基宏.铝网架结构应用研究与实践［J］.建筑钢结构进展，2008，10(1):58-63.

［3］Mazzolani F M.Aluminum Alloy Structure［M］.Florida:CRC Press，1994:1-10.

［4］夏契，熊建武，王德禹.铝合金舟桥甲板结构优化设计［J］.上海交通大学学报:自然科学版，2005，39(5):678-681.

［5］林铸明，夏契，梁川，等.铝合金舟桥甲板结构极限承载能力模型试验与数值分析［J］.力学季刊，2005，25(4): 509-517.

［6］王敏强，薛飞，张桓，等.铰接板梁桥载荷横向分布影响线计算方法［J］.武汉大学学报:工学版，2004，37(4):68-72.

［7］姚玲森.桥梁工程［M］.北京:人民交通出版社，2008:128-140.

［8］姚玲森，程翔云.钢筋混凝土梁桥［M］.北京:人民交通出版社，1982.

［9］Civil Aviation Authority.CAP 437.Offshore Helicopter Landing Areas-Guidance on Standards［S］.CAA.2002.

Theory and Test Study on Transverse Load Distribution of Aluminum Alloy Sandwich Plate Deck Structure

FENG An-tao，ZHOU Xin-gang
(School of Civil Engineering，Yantai University，Yantai 264005，China)

Based on the hinged slab theory，the interactions between aluminum alloy sandwich slabs under lateral load as well as the load distribution are analyzed.Simultaneously，the results are compared with the experimental data.It can be concluded that the deck structure made of sandwich plate behaves much apparently in the interaction under lateral load.The global behavior of the loaded deck can be reflected much better when the influence of load transverse distribution is considered to analyze the stress performance of deck.This analysis plays an important role in the optimization design of deck.

aluminum alloy sandwich panel;load test;transverse load distribution factor;hinged slab theory

TU395

A

(责任编辑 苏晓东)

1004-8820(2015)02-0141-05

10.13951/j.cnki.37-1213/n.2015.02.112

2014-08-04

冯安涛(1989-)，男，山东乐陵人，硕士研究生.

周新刚(ytuzhou@126.com)，教授，博士，从事结构工程方面的研究.