基于自适应牛顿算法的LED视频显示系统的研制

杨 倩, 孙 磊,林志贤, 张永爱

(福州大学 a.至诚学院；b.物理与信息工程学院，福建 福州350002)

基于自适应牛顿算法的LED视频显示系统的研制

杨 倩a, 孙 磊a,林志贤b, 张永爱b

(福州大学 a.至诚学院；b.物理与信息工程学院，福建 福州350002)

LED显示屏已被广泛应用于各种场合，通常情况下，需要对视频图像进行缩放处理，从而符合LED显示屏的物理分辨率。针对传统LED插值缩放算法在插值后导致图像边缘模糊的现象，提出了一种自适应牛顿插值算法，通过在插值之前进行像素相关度的自适应判断，可以较好地保留图像的高频信息，消除图像边缘模糊的问题。同时，给出了基于自适应牛顿算法的LED视频显示系统的FPGA实现，系统最终可以实现较好的显示效果。

自适应牛顿算法；LED；FPGA

目前，大部分LED显示屏均是由LED显示单元(如32×32分辨率)拼接而成，用户可以根据需要拼接成任意分辨率的LED显示屏，然而，若显示的视频图像与LED显示屏的分辨率不同，则会导致视频图像的部分显示或不完整显示，因此，在视频图像显示之前必须对其进行缩放处理[1]，从而使得视频图像的分辨率与LED显示屏的物理分辨率相一致。

传统的插值算法包括最近邻域法、双线性插值法及双立方插值法等，这类插值算法较为简单，易于硬件实现，但是会导致插值后的图像边缘模糊或边缘呈锯齿等现象。而较为高级的插值算法，如变换域插值法、中值滤波器插值法，虽然插值后的图像显示效果较好，但由于算法复杂，而FPGA内部逻辑资源有限，且视频LED显示系统对实时性要求较高，因此，该类算法并不适宜应用于基于FPGA的视频LED显示系统上[2-3]。

本文提出了一种自适应牛顿插值算法，通过在FPGA内进行算法的实现，不仅可以有效地利用FPGA的内部资源，满足视频LED显示系统对实时性的要求。同时，自适应牛顿插值算法可以较好地消除传统牛顿插值算法在插值后导致图像边缘模糊的现象，提高了图像的对比度，显著提高了LED显示屏的显示效果。

1 自适应牛顿插值算法

1.1 传统牛顿插值算法基本原理

设函数f(x)在[a,b]上有定义，则其牛顿插值多项式如

Nn(xi)=f(x0)w0(x)+f[x0,x1]w1(x)+…+

f[x0,x1，…，xn]wn(x)

(1)

在进行图像缩放时，根据式(1)以及所选择的已知像素点数目，即可构建出不同阶数的牛顿插值公式。例如，若选择的

已知像素点为2个，则可构建1阶牛顿插值公式，同理，若选择的已知像素点为3个，则可构建2阶牛顿插值公式。阶数越高，插入点的像素值精度就越高，最终的缩放效果就越好，然而计算过程也更为复杂；阶数越低，插入点的像素值精确度就越低，最终的缩放效果就越差，然而计算过程则相对简单[4]，易于在FPGA内部实现。

1.2 传统牛顿插值算法存在的问题

已知图像中4个点x0，x1，x2，x3的像素值，并要求对图像进行放大操作，利用传统插值算法，若构造2阶牛顿插值多项式，则可以有两种构造方式[5]。

1)方式一

若选用的已知像素点为x0，x1，x2，则构建的2阶牛顿插值多项式为式(2)，此时插入的新像素点如图1所示。

N2(xi)=f(x0)w0(x)+f[x0,x1]w1(x)+

f[x0,x1,x2]w2(x)

(2)

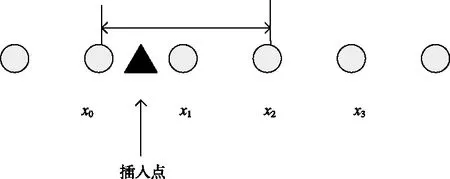
图1 插值方式一

2)方式二

若选用的已知像素点为x1，x2，x3，则构建的2阶牛顿插值多项式为式(3)，此时插入的新像素点如图2所示。

N2(xi)=f(x1)w0(x)+f[x1,x2]w1(x)+

f[x1,x2,x3]w2(x)

(3)

图2 插值方式二

若x0，x1，x2，x3的像素值为180，90，90，90，则根据插值方式一和插值方式二得到的结果如表1所示。

表1 像素值为180，90，90，90的插值结果

由表1可以得出，方式二得到的新插入点的灰度值更好地提高了图像的对比度，使显示效果得到提升。

若x0，x1，x2，x3的像素值为180，180，180，90，则采取上述两种插值方式得到结果如表2所示。

表2 像素值为180，180，180，90的插值结果

由表2可以得出，方式一得到的新插入点的灰度值更好地提高了图像的对比度，使显示效果得到提升。

通过上例可以得出，在不同的情况下，选择方式一或方式二得到的插值结果不同，最终的图像缩放效果也不同，这是因为传统的插值算法并没有考虑到像素之间的联系，建立的是连续的数学模型，因此，图像中的高频信息就会被忽略，得到的图像的边缘势必会变模糊，图像质量因此下降。

1.3 自适应牛顿插值算法原理

定义

(4)

(5)

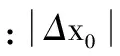
综上所述，自适应牛顿插值算法的公式可以总结如下

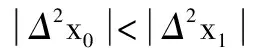
N2(xi)= f(x0)w0(x)+f[x0，x1]w1(x)+

f[x0，x1，x2]w2(x)

(6)

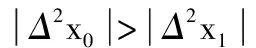
N2(xi)= f(x1)w0(x)+f[x1，x2]w1(x)+

f[x1，x2，x3]w2(x)

(7)

图3a为一幅分辨率为200×200的原始Lena图片，对原始Lena图中方框所示部分(分辨率为50×50)进行缩放，使其分辨率达到200×200。图3b为采用传统的最近邻域法进行缩放的效果图，图3c为采用本文提出的自适应牛顿插值算法进行缩放的效果图，由图可见，采用最近邻域法放大后的图像边缘呈锯齿状，而采用自适应牛顿插值算法后，图像边缘光滑，消除了边缘呈锯齿状的问题，且对比度提高，提升了显示效果。

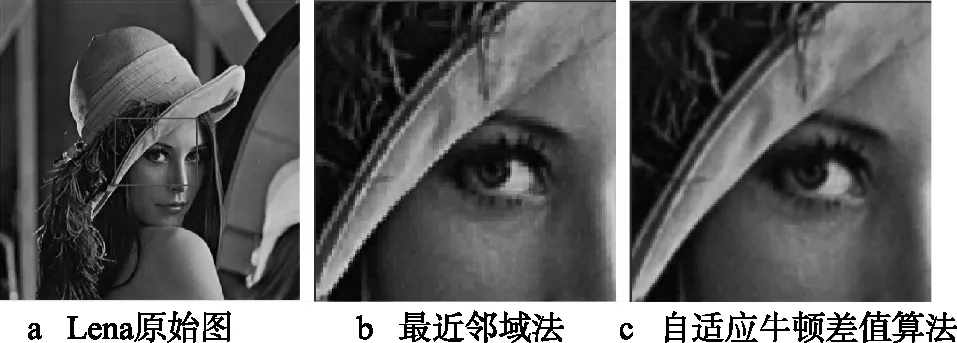
图3 不同缩放算法效果图

对于一幅二维图像，首先进行水平方向的自适应牛顿插值处理，再进行垂直方向的自适应牛顿插值处理，其处理方式如图4所示。

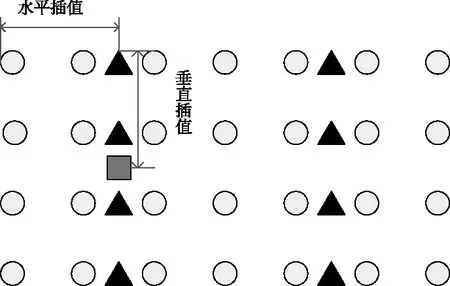
图4 二维图像自适应牛顿插值处理方式

2 基于自适应牛顿算法的LED视频显示系统

视频LED显示系统的主控部分采用FPGA实现[6-7]，系统主要包含算法处理模块和读写控制模块两大模块，FPGA软件控制框图如图5所示。

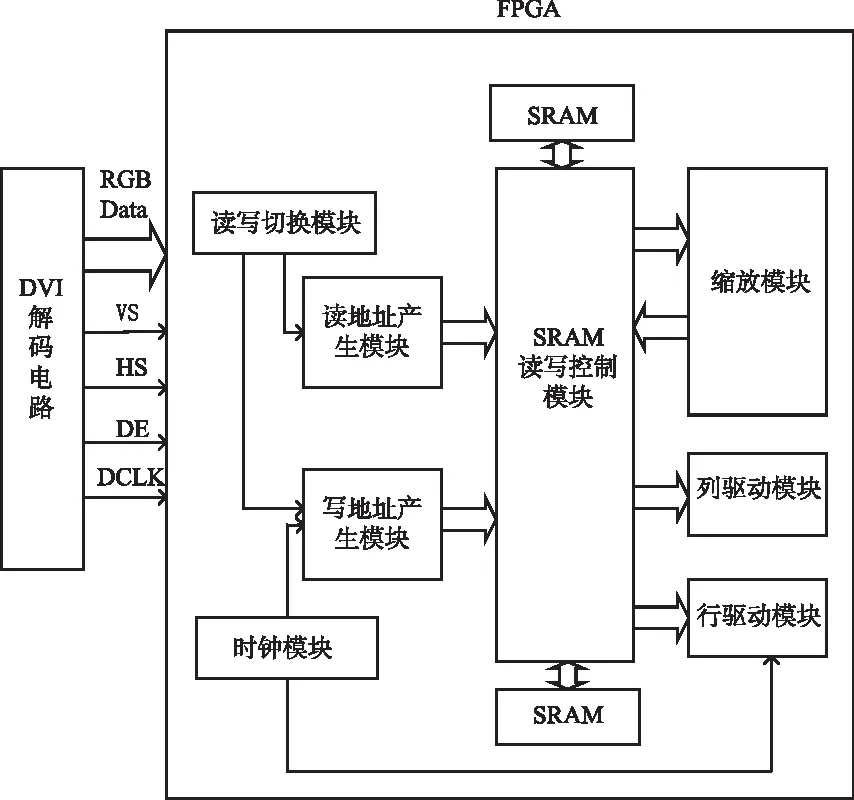
图5 FPGA软件控制框图

2.1 算法处理模块

为了满足视频LED显示系统对实时性的要求，并考虑到FPGA内部资源的有限性，本次设计采用2阶自适应牛顿算法对视频图像进行缩放处理。算法处理模块包含判别子模块、系数生成子模块和选择子模块，其算法流程图如图6所示。

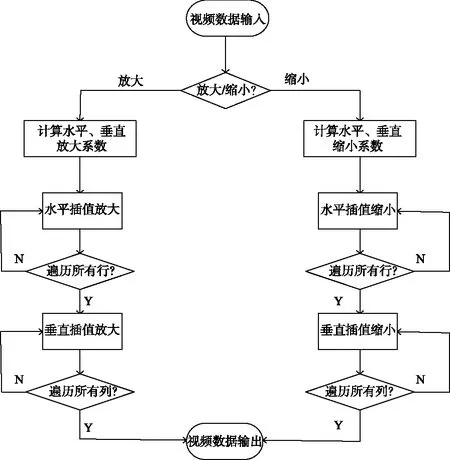
图6 算法流程图

算法的具体流程为：设输入视频数据分辨率为800×600，而LED显示屏的物理分辨率为1 280×1 080，则需要对每一帧视频图像进行放大插值处理，即将行方向放大为原先的1.6倍，列方向放大为原先的1.8倍。设m为放大系数，则放大系数表示为

m=1/放大倍数

(8)

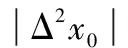
2.2 读写控制模块

读写控制模块接收读地址产生子模块产生的读地址和写地址产生子模块产生的写地址。读写控制模块对数据的读写采用乒乓机制，即向其中一片SRAM写入3D视频数据的同时从另一片SRAM中读取数据。同时，读写控制子模块还会接收读写切换子模块产生的读写切换信号，当读写切换信号发生跳变时，读写控制模块对两片SRAM的读写状态进行切换。

读写控制模块的波形仿真结果如图7所示。其中，add1，data1，we1，oe1，ce1是SRAM1的地址线、数据线、写信号、读信号和选通信号；add2，data2，we2，oe2，ce2是SRAM2的地址线、数据线、写信号、读信号和选通信号。wadden是写地址有效信号，每当wadden翻转一次，代表产生了新的有效的写地址，需要进行写操作；radden是读地址有效信号，每当wadden翻转一次，代表产生了新的有效的读地址，需要进行读操作。

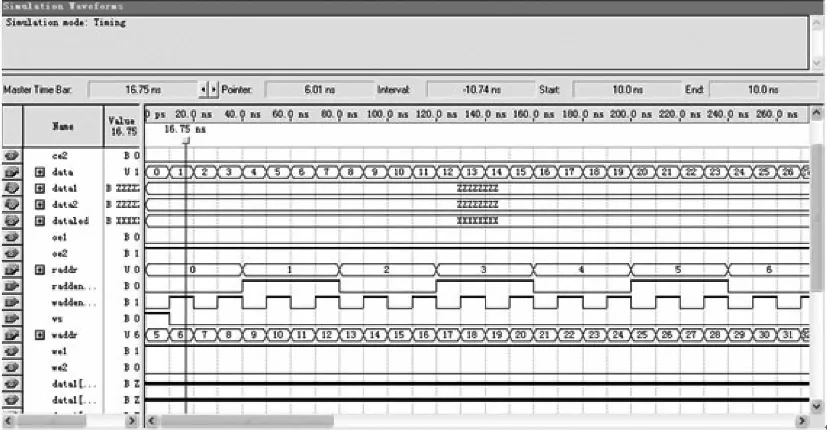
图7 读写控制模块的波形仿真结果(截图)

本设计采用型号为EP1C6Q24C08的FPGA作为系统的主控部分，图8是分辨率为256×128的LED显示屏，视频源的分辨率为600×480，采用自适应牛顿插值算法对图像进行缩放处理，系统最终可以实现较好的显示效果。

图8 LED显示屏

3 结束语

本文提出了一种自适应牛顿插值算法，通过在插值之前进行像素相关程度的自适应判断，可以较好地消除传统牛顿插值算法在插值后导致图像边缘模糊的现象。同时，本文给出了基于自适应牛顿算法的LED视频显示系统的FPGA实现，该算法有效提高了LED显示图像的对比度，最终实现较好的显示效果。

[1]诸昌钤.LED 显示屏系统原理及工程技术[M].成都：电子科技大学出版社，2000.

[2] XIAO Jianping, ZOU Xuecheng, LIU Zhenglin, et al.Adaptive interpolation algorithm for real-time image resizing[C]//Proc.First International Conference on Innovative Computing, Information and Control (ICICIC′06).[S.l.]:IEEE Press，2006：221-224.

[3]胡敏,张佑生.Newton-Thiele插值方法在图像放大中的应用研究[J].计算机辅助设计与图形学学报, 2003, 15(8)：1004-1007.

[4]刘正林，肖建平，邹雪城，等.基于边缘的实时图像缩放算法研究[J].中国图象图形学报，2008，13(2)：225-229.

[5]王慧中，吴永欣，茹运蕊，等.带有外同步输入的图像处理和实时显示系统[J].电视技术,2010,34(4)：45-47.

[6]龚兆岗.基于ARM处理器的LED可变情报板嵌入式控制器[J].现代显示，2006，64(6)：163-16.

[7]李天华.大型LED显示屏的计算机辅助矫正[J].电视技术，2011，35(17)：65-68.

责任编辑：许 盈

Research of LED Display System Based on Adaptive Newton Interpolation Algorithm

YANG Qiana, SUN Leia, LIN Zhixianb, ZHANG Yong′aib

(a.ZhichengCollege;b.CollegeofPhysicsandInformationEngineering,FuzhouUniversity,FujianFuzhou350002,China)

LED display has been widely used in various occasions.Usually, it is inevitable to apply the zooming algorithm to the video image so as to fit the physical resolution of the LED display.According to the problems that traditional interpolation zooming algorithm used in LED leads to the blurring edge of the image, an adaptive Newton interpolation algorithm is presented in this paper.Through adaptive judgment of the relevance between pixels before interpolation, the high-frequency information can be better reserved and the blurring edge of the image can be effectively eliminated.Meanwhile, the realization of LED display system based on FPGA is designed.The system shows satisfying display effect.

adaptive Newton algorithm; LED; FPGA

TN949.16; TN941.3

A

10.16280/j.videoe.2015.05.019

国家“863”计划项目(2012AA03A301；2013AA030601)；福建省自然科学基金项目(2013J01236)；福州大学科技发展基金项目(2013-XQ-41)

杨 倩，女，助教，主要研究方向为信息显示技术；

孙 磊，女，讲师，主要研究方向为信息显示技术，为本文通讯作者；

林志贤，教授，主要研究方向为信息显示技术；

张永爱，副研究员，主要研究方向为信息显示技术，为本文通讯作者。

2014-06-27

【本文献信息】杨倩，孙磊，林志贤，等.基于自适应牛顿算法的LED视频显示系统的研制[J].电视技术,2015，39(5).