表面扩散下铜内沿晶微裂纹演化的数值模拟

杜杰锋，黄佩珍

（南京航空航天大学机械结构力学及控制国家重点实验室，江苏南京 210016）

表面扩散下铜内沿晶微裂纹演化的数值模拟

杜杰锋，黄佩珍

（南京航空航天大学机械结构力学及控制国家重点实验室，江苏南京 210016）

基于表面扩散和蒸发－凝结的经典理论及其弱解描述，对应力诱发表面扩散下铜内沿晶微裂纹演化进行了有限元分析。结果表明：沿晶微裂纹演化分节存在临界外载和临界形态比，当外载或形态比小于临界值时，微裂纹逐渐圆柱化；当外载或形态比大于等于临界值时，微裂纹沿晶界方向扩展并分节为三个裂腔。微裂纹分节时间随外载的增大和形态比的增大都减小，即外载和形态比的增大加速微裂纹分节。而临界外载和临界形态比随着形态比或外载的增大而减小，表明形态比和外载的增大都将有助于微裂纹分节。此外，沿晶微裂纹中晶界能与表面能比值的增大会加快微裂纹的分节。

沿晶微裂纹；表面扩散；应力迁移；有限单元法；裂腔分节

1 引 言

金属中晶内、晶界孔洞的萌生、扩张、连接或者失稳会形成裂纹型缺陷，这是导致微电子器件中薄膜导线失效的关键因素之一。晶界是应力集中、裂纹萌生和扩展的重要位置，晶界的存在将对金属材料内部微裂纹演化过程产生重要影响。Hull和Rimmer［1］首次建立了一个球状晶界孔洞在拉应力作用下由晶界扩散控制的孔洞长大模型。此后的工作中主要是发展数值方法，如使用有限差分法、有限元法等对孔洞、裂纹演化过程进行数值模拟［2－5］。包含表面扩散和蒸发－凝结机制的有限元方法首次由Sun和Suo［6］提出，沿用此方法，He等［7］通过研究发现拉压应力作用下的晶内微裂纹也会发生裂腔分节现象。徐春风等［8］研究了电作用下沿晶微裂纹系统的演化。

本文基于材料微结构演化的有限元理论，详细分析了外载、形态比以及晶界能与表面能比值对沿晶微裂纹演化的影响。

2 二维沿晶微裂纹模型

图1所示为双向受拉外载作用下沿晶微裂纹模型。裂纹形貌由形态比β＝a／h0确定，其中a与h0分别为椭圆在x、y方向上的半轴长。晶界与裂面的连接处满足力的边界条件：

图1 应力场下沿晶微裂纹的简化模型Fig.1 A simp lified model of an intergranular m icrocrack under stress field

式中：2θ为裂尖裂面的二面角，γs为表面能，γb为晶界能。

3 基本理论

3.1 表面扩散及蒸发－凝结的弱解描述

当微结构固体表面同时存在表面扩散和蒸发－凝结两种质流过程时，表面扩散驱动力F与蒸发凝结驱动力p作用下系统自由能的减少量－δG为［2］：

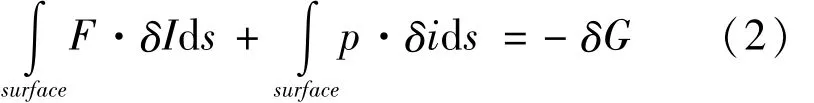
其中，δI是表面扩散下的物质虚位移，δi是蒸发－凝结下的表面法向虚位移。

根据Herring［9］理论，采用线性动力学原理：

其中J为表面扩散的流量，j为表面法向速度，M与m分别为表面扩散与蒸发－凝结的原子迁移率。

结合线性动力学原理和质量守恒定理，表面扩散与蒸发－凝结机制下的弱解描述为［6］：

在如图1所示的模型中，系统的总自由能仅包括表面能、晶界能和应变能：

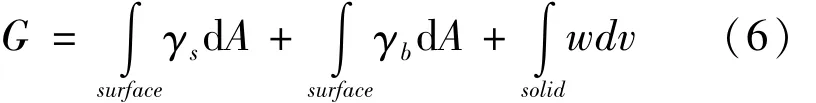
式中：：γs是表面能，γb是晶界能，w是应变能密度。

3.2 有限元方法

本文研究的二维微裂纹表面可近似为许多线性单元，节点的坐标及物质位移I形成广义坐标qi，广义速度为表面虚位移则可表示为δqi。对式（5）进行积分，左端可得含及δq的双线性型表达式，右端则为关于虚位移的总自由能变化：

其中：fi为广义力。两端消去δqi后可得：

基于以上控制方程，如给定当前构形的沿晶微裂纹，使用当前的广义坐标计算式中的粘度矩阵H以及载荷向量f，通过迭代求解得出各节点的速度，已知节点速度，对于给定的微小时间增量Δt，可得到更新表面的节点位移。循环该过程，就可模拟沿晶微裂纹的形貌演化。

4 数值计算

计算中选取各向同性线弹性铜材料参数［10］：E＝130GPa，ν＝0.33，γs＝1.725J／m2，γb＝0.654J／m2，外载为双向等值受拉（σx＝σy＝σ）。为方便，采用无量纲化应力：和无量纲化时间

4.1 外载对沿晶微裂纹演化的影响

对比图2（a）和（b）可知，微裂纹在不同外载下存在一个临界外载：当时，裂纹逐渐圆柱化；当时，微裂纹将会沿晶界方向拓展并最终分节为三个裂腔。

图4给出了不同形态比下晶内微裂纹与沿晶微裂纹发生裂腔分节的临界载荷由图4可见，随着β的增大，晶内与沿晶微裂纹发生裂腔分节所需要的都逐渐减小，说明大裂纹更易发生分节。对比相同形态比的晶内微裂纹和沿晶微裂纹，前者临界载荷大于后者的临界载荷。

图2 β=10时沿晶微裂纹的演化Fig.2 The evolution of the intergranular m icrocrack forβ=10

图3 分节时间随外载的变化Fig.3 The splitting timeas a function of)σ

4.2 形态比对沿晶微裂纹演化的影响

由图5（a）可见，当β较小时，沿晶微裂纹未发生裂腔扩展，而是长轴逐渐缩短，趋于圆柱化；随着β的增大，沿晶微裂纹会逐渐沿晶界扩展，并最终分节为三个裂腔。

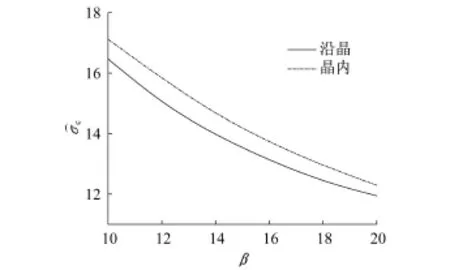
图4 随β的变化Fig.4as a function ofβ

图5 时沿晶微裂纹的演化Fig.5 The evolution of the intergranular m icrocrack for

由图6可见，当外载比较小时，微裂纹分节时间随形态比的增大而减小。由图6中)σ＝22的曲线可以看出，当外载比较大时，由于沿晶微裂纹快速分节，形态比对分节时间的影响可忽略不计。

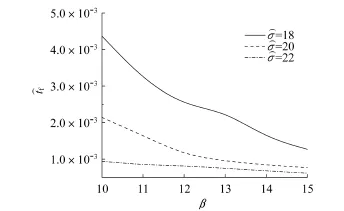
图6 分节时间随β的变化Fig.6 The sp litting timeas a function ofβ

图7 βc随的变化Fig.7 βcas a function of)σ

4.3 晶界能与表面能比值对裂纹演化的影响

5 结 论

本文应用应力诱发表面扩散主导微结构演化的有限单元法数值模拟了双向受拉铜材料内部沿晶微裂纹的演化，得出结论如下：

图8 随的变化Fig.8as a function of)γ

（3）沿晶微裂纹比晶内微裂纹更易发生分节。

［1］ Hull D，Rimmer D E.The growth of grain－boundary voids under stress［J］.Philosophical Magazine，1959，4（42）：673－687.

［2］ Liu Z，Yu H.A numerical study on the effect of mobilities and initial profile in thin film morphology evolution［J］.Thin Solid Films，2006，513（1-2）：391－398.

［3］ Bower A F，Shankar S.A finite element model of electromigration induced void nucleation，growth and evolution in interconnects［J］.Modelling and Simulation in Materials Science and Engineering，2007，15（8）：923－940.

［4］ Liu Z，Yu H.Stress relaxation of thin film due to coupled surface and grain boundary diffusion［J］.Thin Solid Films，2010，518（20）：5777－5785.

［5］ Huang P Z，Zhang Z Z，Guo JW，et al.Axisymmetric finite-element analysis for interface migration-controlled shape instabilities of plate-like double-crystal grains［J］.Advanced Materials Research，2012，460：230－235.

［6］ Sun B，Suo Z.A finite element method for simulating interfacemotion—II.Large shape change due to surface diffusion［J］.Acta materialia，1997，45（12）：4953－4962.

［7］ Dingni He，Peizhen Huang.A finite-element analysis of intragranular microcracks in metal interconnects due to surface diffusion induced by stress migration.Comp.Mater.Sci，2014，87：65－71.

［8］ 徐春风，黄佩珍.力、电作用下沿晶微裂纹系统演化的仿真分析［J］.系统仿真技术，2012，8（2）：99－104.XU Chunfeng，HUANG Peizhen.Simulation and Analysis of the Evolution of Transgranular Microcracks System Induced by Stress and Electric Field［J］.System Simulation Technology，2012，8（2）：99－104.

［9］ Herring C.Surface tension as amotivation for sintering，Kingston WE，The Physics of Powder Metallurgy，1951［Z］.McGraw-Hill，New York，1951.

［10］ Shibutani T，Kitamura T，Ohtani R.Creep cavity growth under interaction between lattice diffusion and grainboundary diffusion［J］.Metallurgical and Materials Transactions A，1998，29（10）：2533－2542.

杜杰锋 男（1990－），浙江绍兴人，硕士，主要研究方向为微结构演化。

黄佩珍 女（1972－），浙江浦江人，教授，博士，主要研究方向为工程问题的力学建模与数值仿真。

Numerical Simulation of the Intergranular Microcracks Evolution in Copper Due to Surface Diffusion

DU Jiefeng，HUANG Peizhen

（State Key Laboratory of Mechanics and Control of Mechanical Structures，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China）

Based on the classical theory of surface diffusion and evaporation-condensation along w ith its weak statement，a finite element program is developed for simulating the evolution of intergranular microcracks in Copper due to surface diffusion induced by stressm igration.The results show that there exists critical values of the stress and the aspect ratiofor the intergranular microcrack under the biaxial tensile stress.When the stress or the aspect ratio is less than the critical values，the microcrack w ill directly evolve into a cylinder.When the stress or the aspect ratio is equal or greater than the critical values，itw ill grow and split into three smallmicrocracks along the grain boundary.The splitting time of the intergranularm icrocrack reduces w ith increasing the stress or the aspect ratio，which means that the increase of the stress and the aspect ratio w ill accelerate the splitting process.The critical values of the stress and the aspect ratio decrease when the tress and the aspect ratio increase，that is，the increases of the stress and the aspect ratio are beneficial to themicrocrack splitting.In addition，the higher of the ratio between the grain-boundary energy and the surface energy，the shorter of the splitting time w ill be.

intergranular microcrack；surface diffusion；stress m igration；finite element method； microcrack splitting

TG 113

A

江苏省自然科学基金资助项目（BK20141407）；江苏高校优势学科建设工程资助项目