让学生的思维插上翅膀
王丽静
一位著名的数学教育家曾形象地指出:“好问题同种蘑菇类似,它们都成堆地生长,找到一个以后,你应当在周围找一找,很可能附近就有好几个。”由此,我不禁联想到我们的数学教学,不能仅仅是就题论题,而应多角度、多层次地提出问题。
我在讲解了“圆的有关性质”后,为了检测学生的掌握情况,我出示了这样一题:
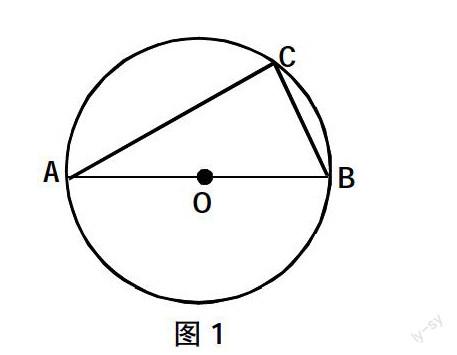
如图1,在△ABC中,AB是⊙O的直径,∠A=30°,BC=2,求⊙O的半径。
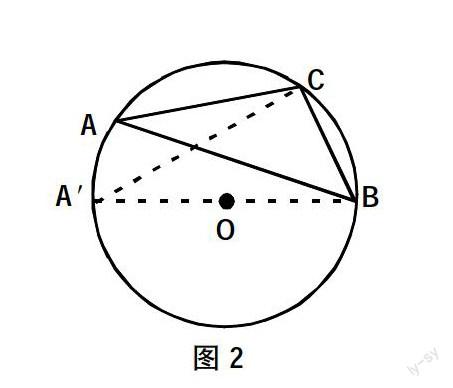
有的学生“唰”地把小手举了起来,有的在下面小声说:“这题太简单了,就是一道解直角三角形的题。”我便叫了一名學生,他胸有成竹地说:“因为AB是⊙O的直径,所以可知△ABC为直角三角形。∵BC=2,∠A=30°∴AB=4,∴⊙O的半径是2。”我知道该生很聪明,希望他的思维不只是停留在问题的表面,便问:“如果题中AB不是⊙O的直径,其余条件不变,那么半径还会是2吗?”该生不假思索地说:“AB不是⊙O的直径,当然不能解直角三角形了,所以⊙O的半径不会是2了。”其他学生也觉得他说得有道理。其实这就是思维的定式,也正是我们应该提醒学生注意的地方。于是,我启发道:“想一想,这个圆中会不会有上题中那样的直角三角形出现呢?”此时学生陷入了思考。圆的直径所对的圆周角是直角,故有多个直角三角形供选择,但所构造的直角三角形,必须用到已知三角形的条件,于是学生会试着过A,B,C三点画直径,直至发现⊙O的半径还是2。另一个学生一脸兴奋地说:“如图2,作直径A′B,联结A′C即可。和原来的直径一样!”此时,我又趁热打铁,引领学生的思维往前再走一步。“若设∠A=α,BC=a。则⊙O的直径是多少?”此时的学生有了上面的经验,不难得出⊙O的直径2r=asinα。最后,我让学生小组合作总结上述问题的解决过程,你学到了哪些方法?从这三个问题中,你发现了什么?这样设计让学生在课堂活动中感悟到知识的生成、发展与变化的过程,帮助他们在自主探索与合作交流的过程中真正理解和掌握基本的数学知识与技能、数学思想与方法,获得广泛的数学经验和成功的体验。
试想,如果在做完第一个题时,学生答得比较完美,教师就此戛然而止,从教学效果上看也不错,但我们总觉得少了点什么?“简单”的背后学生收获了什么?难道仅仅是让学生会求圆的半径吗?如果是这样的话,那与求解直角三角形有什么区别?为何不让学生的思维走得更深、更远呢?
有人说:“数学是思维的体操。”初中数学教学中,对学生思维能力的训练既可以增强学生的创新意识,又可以培养学生的创新能力,还可以培养学生实事求是的科学态度。作为一名数学教师,我时刻告诫自己:深挖一锹就会出水,努力让学生的思维多走一步。让学生的思维插上翅膀!
?誗编辑 杨兆东

