城市天然气月用量的预测方法

梁金凤，郭开华，皇甫立霞

（中山大学工学院，广东 广州510275）

引 言

在我国的燃气输配设施规划设计中，仅以不均匀系数进行月用气量估算，方法粗略且缺少可靠性。当前国内外的研究主要集中在年用气量预测［1－6］以及 日、 小 时 用 气 量 预 测［7－14］方 面， 使 用 的方法有传统的 （非）线性回归方法［15－17］以及神经网络［18－20］、 遗 传 算 法［21－22］等 一 些 现 代 智 能 算 法，建立的预测模型仅适用于发展稳定的城市，或多为趋势外推类方法，更适用于日常调度的短期精准预测。本研究针对我国快速发展中城市的用气量变化特点建立月用气量预测模型，并对不同类型城市的预测模型进行参数分析及实际应用，对我国城市燃气输配设施的规划设计提供参考。

1 用气量变化规律数学描述

城市用气量的发展变化具有 “有限制增长”特点和周期变化规律。在城市区域不变的条件下，我国绝大多数城市用气量处于快速增长阶段，但天然气作为能源供应量是有限的，因此城市用气量的增长具有一定的上限。同时，由于人的生活或生产活动具有时间周期变化特点，城市用气量的变化也具有周期性。

1.1 用气量变化规律

1.1.1 用气量的增长变化规律 城市用气量的发展变化过程与自然界的物种演变过程以及人类社会的经济发展变化过程相似，具有S形曲线变化特点，可用逻辑斯蒂方程表征。

1.1.2 用气量的周期变化规律 城市用气量具有以12个月为周期的变化规律，单位周期内具有高峰特征值和低谷特征值。

1.2 用气量变化规律的数学描述

1.2.1 用气量增长变化规律的数学描述 以年为基础时间单位，设定年用气量初始值为Qy0、年用气量极限值为Qylim，年用气量同比增长率为ry，基于逻辑斯蒂原理［23－24］，描述用气量的增长变化规律，并得到年用气量的计算表达式

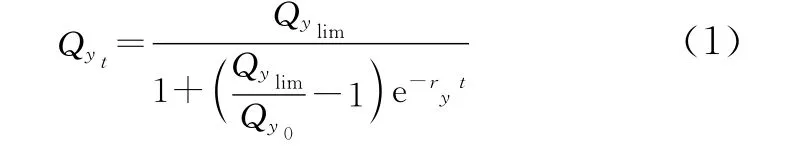
1.2.2 用气量周期变化规律的数学描述 以12个月为单位周期，月用气量与年用气量的比值作为该月用气量的特征值。设月用气量的高峰特征值为crmmax、低谷特征值为crmmin，根据单位周期内月用气量变化特点给出月用气量变化分布曲线fcrm（tm）的表达式

2 月用气量预测模型

在已知年用气量的前提下，根据月用气量变化分布曲线可得城市月用气量计算方法，实现城市月用气量的预测。

以月为基础时间单位的年用气量计算公式为

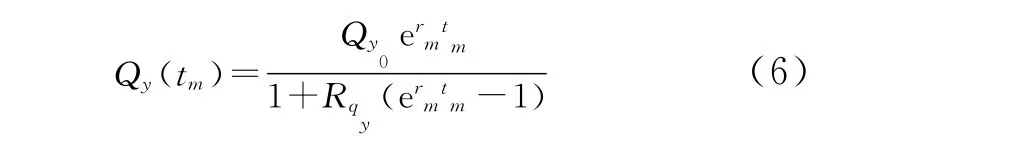
由此得到城市月用气量预测公式

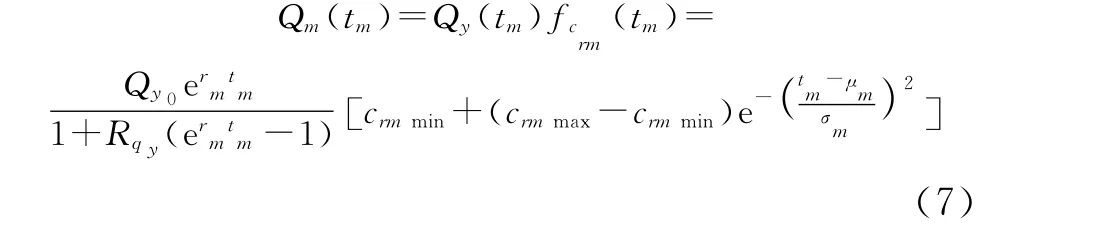
3 预测模型的参数分析

在年用气量确定的条件下，影响月用气量预测值的参数主要有月用气量高峰特征值crmmax、低谷特征值crmmin、高峰时刻μm以及月用气量变化分布曲线宽度σm，即月用气量变化分布曲线决定了月用气量的实际变化形态。crmmax与crmmin决定了月用气量的变化范围，μm决定了月用气量最大值的位置点，σm决定了月用气量的变化幅度。显然不同类型城市的月用气量变化分布曲线特征各异。

3.1 生活类城市预测模型的参数分析

民商用户用气量占比大的城市可视为生活类城市，主要采用天然气进行炊事和采暖。是否集中采暖决定了月用气量变化分布曲线高峰特征值与低谷特征值之间的差距，即集中采暖的城市月用气量变化分布曲线高程差相对突出，没有集中采暖的城市月用气量变化分布曲线相对平缓。

如图1所示，HC市为集中采暖类城市，GK市为非集中采暖类城市。可以看出，集中采暖类城市冬季用气量高峰明显，用气量变化剧烈，采暖期的开始与结束对城市用气量影响巨大；非集中采暖类城市用气量变化波动相对小，高峰值与低谷值相差不大，但用气量高峰依然出现在冬季12月，说明冬天人们生活对热量的需求显著。不同城市高峰时刻位置点略有不同，但都在12月或1月左右。

图1 生活类城市月用气量变化分布曲线Fig.1 Distribution curve of life city monthly nature gas consumption

3.2 生产类城市预测模型的参数分析

工业用户用气量占比大的城市可视为生产类城市，主要采用天然气进行工业生产活动。生产类城市工业用户用气量占比大，但是冬季是否集中采暖仍是影响月用气量不均匀性的主要原因，对于生产类城市也应区分是否集中采暖。对于完全生产类城市，城市用气量变化特征实际表现的是工业用户用气量的变化特征。因此将生产类城市再细分为是否集中采暖以及完全生产3类。

如图2所示，HS市为集中采暖的生产类城市，可以看出冬季用气量不均匀性较大。用气高峰特征值高达0.18，低谷特征值与其他城市相差不大，而且高峰过后用气量急剧降低，月用气量变化曲线后坡宽度较小，说明从用气量高峰值下降到低谷值所用时间短，用气量变化快速。此外，生产类城市在1月或2月用气量会出现超常规降低，说明春节对生产类城市用气量影响显著。

图2 集中采暖生产类城市 （HS）月用气量变化分布曲线Fig.2 Distribution curve of centralized heating production city（HS）monthly nature gas consumption

AB市为无集中采暖的生产类城市 （图3）。与集中采暖城市相比，AB市的冬、夏季用气不均匀性相对较小，但工业用户春节期间用气量降低的特点依然明显。

图3 非集中采暖生产类城市 （AB）月用气量变化分布曲线Fig.3 Distribution curve of non centralized heating production city（AB）monthly nature gas consumption

GD和FQ市为完全生产类城市 （图4），此类城市工业用气已占城市用气总量的80%以上，城市用气量的变化特征实为工业用户的用气量变化特征。此类城市的月用气量在单位周期内有明显的两个高峰和低谷，月用气量变化曲线具有极强的个体性。

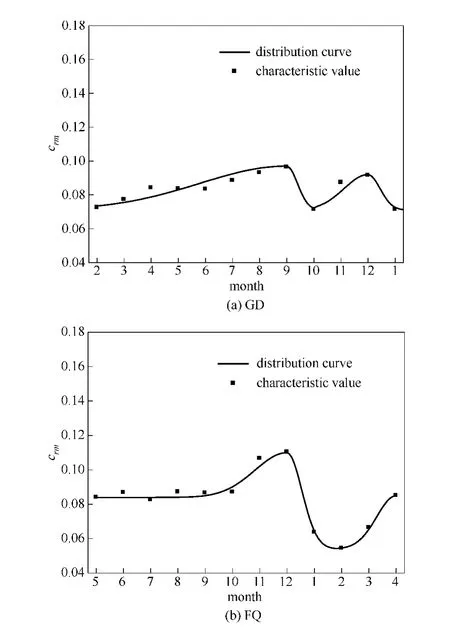
图4 完全生产类城市月用气量变化分布曲线Fig.4 Distribution curve of entire production city monthly nature gas consumption

3.3 综合类城市预测模型的参数分析

民商用户与工业用户用气量相当的城市可视为综合类城市。它既有民商用户随季节变化的高峰、低谷用气特征，又有工业用户用气较平稳的特征，两种特征交织在一起，使此类城市看起来同时具有两种城市特征但程度又不强。

根据SL市多年历史数据得到月用气量特征值，采用式 （4）对特征值进行计算，得到月用气量变化分布曲线，如图5所示。SL市冬季集中采暖期短，而且采暖用气量相对小。由于工业用户受春节影响，城市用气量在1月左右出现急剧下降情况。

4 预测模型的实际应用

4.1 HC市月用气量的预测

4.1.1 HC城市概况 HC市属亚热带季风气候，年平均气温17.2℃，由于城市社会经济发展水平较高，冬季出现短期采暖且天然气使用量较大。HC市从2005年起大规模使用天然气，燃气发展迅速，民用和商业用户用气占主导地位，约为城市总用气量的70%。

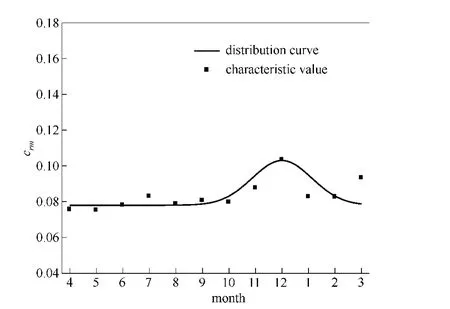
图5 综合类城市 （SL）月用气量变化分布曲线Fig.5 Distribution curve of comprehensive city （SL）monthly nature gas consumption

4.1.2 HC市月用气量预测模型参数 根据城市实际用气量的变化情况对预测模型的参数进行设定，其中：年用气量增长率ry＝0.26year－1，年用气量 （标准状况，下同）初始值Qy0＝1.4×108m3，年用气量极限值Q＝25×108m3，月高峰

ylim特征值crmmax＝0.133，月低谷特征值crmmin＝0.065，年高峰对应月μm＝1.02month；月用气量变化分布曲线前坡宽度σm1＝1.4month，后坡宽度σm2＝2.2month。

4.1.3 HC市月用气量预测结果 已知预测模型的计算参数，根据式 （7）对HC市2012～2013年的月用气量进行预测计算，结果见表1。

4.2 JH市月用气量的预测

4.2.1 JH城市概况 JH市兼有南北气候特征，全市年平均气温为14.5℃。JH市从2002年起大规模使用天然气，燃气发展相对稳定。城市总用气量的45%为工业用户生产用气，城市总用气量的40%为民商用户生活用气。

4.2.2 JH市月用气量预测模型参数 根据城市实际用气量的变化情况对预测模型的参数进行设定，其中：年用气量增长率ry＝0.22year－1，年用气量初始值Q＝0.17×108m3，年用气量极限

y0值Q＝5×108m3；月高峰特征值crmmax＝0.1，ylim月低谷特征值crmmin＝0.08，年高峰对应月μm＝12month；月用气量变化分布曲线前坡宽度σm1＝2month，后坡宽度σm2＝0.5month。

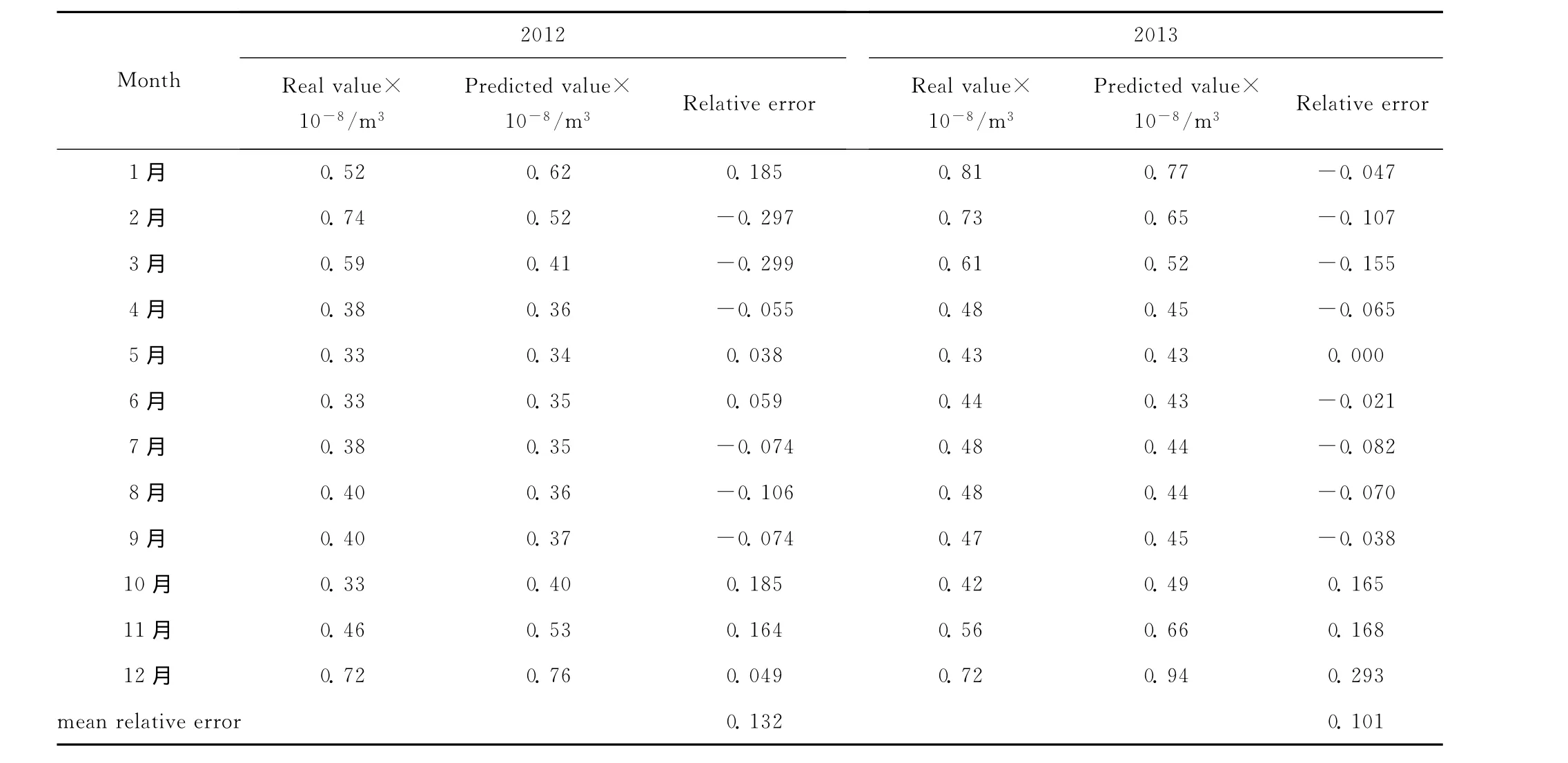
表1 2012～2013年HC市月用气量预测结果Table 1 Predicted results of city HC's monthly nature gas consumption in 2012—2013

表2 2012～2013年JH市月用气量预测结果Table 2 Predicted results of city JH's monthly nature gas consumption in 2012—2013

4.2.3 JH市月用气量预测结果 已知预测模型的计算参数，根据式 （7）对JH市2012～2013年的月用气量进行预测计算，结果见表2。

4.3 预测误差的评价

根据表3中的误差评价指标，对建立的城市月用气量预测模型进行精度评价。表3的数据显示，预测模型的后验差小于0.35，小误差概率大于0.95，判定精度等级为一级优秀。

表3 预测误差的统计分析Table 3 Statistical analysis of forecast error

5 结 论

（1）城市天然气用量具有 “有限制增长”特点及以12个月为周期的变化规律，单位周期内存在高峰特征值和低谷特征值。

（2）本研究建立的月用气量预测模型体现了城市天然气月用气量的变化特点和规律，适用于城市燃气输配设施的规划设计。

（3）不同类型城市月用气量变化分布曲线的特征值及其变化范围各异，而且高峰点前后曲线宽度不同。集中采暖类城市月用气量具有明显的高峰特征值，而且高峰特征值与低谷特征值相差范围较大。非集中采暖类城市月用气量的高峰特征值与低谷特征值相近。完全生产类城市月用气量具有明显的个体特点。

（4）对HC和JH市2012～2013年的月用气量进行预测，平均相对误差为9.7%，模型后验差为0.15，小误差概率为0.98，精度等级为一级优秀。

符 号 说 明

crm（tm）——tm月用气量特征值

fcrm（tm）——月用气量变化分布曲线函数

Qmmax——月用气量高峰值，m3

Qmmin——月用气量低谷值，m3

Qm（tm）——tm月用气量，m3

Qy——年用气量，m3

——年用气量极限值，m3

——年用气量初始值，m3

ry——年用气量同比增长率，year－1

tm——基础时间单位，month

μm——高峰用气量对应月，month

σm——月用气量变化分布曲线宽度，month下角标

m——月份 （m＝1，2，…，12）

max——高峰值

min——低谷值

y——年 （y＝0，1，…，lim）

［1］ Mbamalu G A N，El－Hawary M E.Load forecastingviasuboptimal season models and iteratively reweighted least squares estimation ［J］.IEEETransationsonPower Systems，1993，8 （1）：343－348.

［2］ David R Brillinger.Time Series Data Analysis and Theory［M］.Berkeley：University of California at Berkeley，2001.

［3］ David Gottlieb，Steven A Orszag.Numerical Analysis of Spectral Methods：Theory and Applications（Sixth Printing）［M］. USA：the Society for Industrial and Applied Mathematics，1993.

［4］ Gorucu F B，Gumrah F.Evaluation and forecasting of gas consumption by statistical analysis ［J］.AppliedEnergy，2004，26 （3）：267－276.

［5］ Sahbi Farhani， Muhammad Shahbaz， Mohamed Arouri，FrédéricTeulon.The role of natural gas consumption and trade in Tunisia's output［J］.EnergyPolicy，2014，66：677－684.

［6］ Himadri Shekhar Dey，Md Ashfanoor Kabiry，Zia Wadudz，Shahidul Islam Khany，Md Abul Kalam Azad.Econometric modeling and forecasting of natural gas demand for power sector in Bangladesh／／TENCON 2011—2011IEEE Region 10Conference ［C］.2011：1383－1386.

［7］ Sabo K，Scitovski R，Vazler I，etal.Mathematical models of natural gas consumption ［J］.EnergyConversionand Management，2011，52 （3）：1721－1727.

［8］ Eugenio Fco Sánchez－＇Ubeda，Ana Berzosa.Modeling and forecasting industrial end－use natural gas consumption ［J］.EnergyEconomics，2007，29：710－742.

［9］ Marek Brabec，Ondˇrej Konár，Emil Pelikán，Marek Mal＇y.A nonlinear mixed effects model for the prediction of natural gas consumption by individual customers ［J］.International JournalofForecasting，2008，24：659－678.

［10］ Marina Theodosiou.Disaggregation ＆aggregation of time series components：a hybrid forecasting approach using generalized regression neural networks and the theta method［J］.Neurocomputing，2011，74：896－905.

［11］ Petr Musilek， Emil Pelikán， Tomáš Brabec， Milan Šim°unek.Recurrent neural network based gating for natural gas load prediction system／／International Joint Conference on Neural Networks ［C］.Vancouver，Canada，2006：3736－3741.

［12］ Božidar Soldo， Primož Potoˇcnik， Goran Šimunovi＇c，TomislavŠari＇c，Edvard Govekar.Improving the residential natural gas consumption forecasting models by using solar radiation ［J］.EnergyandBuildings，2014，69：498－506.

［13］ Papalxopoulos A D，Hesterberg T C.A regression based approach to short term system load forcasting ［J］.IEEE TransactionsonPowerSystems，1990，5 （4）：1535－1547.

［14］ Pahasa J，Theera－Umpon N.Short－term load forecasting using wavelet transform and support vector machines ［J］.2007ConferenceProceedingsIpec，2007，（1－3）：47－52.

［15］ Gorucu F B，Gumrah F.Evaluation and forecasting of gas consumption by statistical analysis ［J］.EnergySources，2004，26 （3）：267－276.

［16］ Gutiérrez R，Nafidi A，Gutiérrez Sánchez R.Forecasting total natural－gas consumption in Spain by using the stochastic Gompertz innovation diffusion model［J］.AppliedEnergy，2005，80（2）：115－124.

［17］ Vondracek J，Pelikan E，Konar O.A statistical model for the estimation of natural gas consumption ［J］.Applied Energy，2008，85 （5）：362－370.

［18］ Martin Anthony.Discrete Mathematics of Neural Networks Selected Topics ［M］.Philadelphia：Society for Industrial and Applied Mathematics，2001.

［19］ The Intelligent Network： Current Technologies，Applications，and Operations ［R］.USA：International Engineering Consortium，1997.

［20］ Demirel O F，Zaim S，Caliskan A.Forecasting natural gas consumption in Istanbul using neural networks and multivariate time series methods ［J］.TurkishJournalofElectricalEngineeringandComputerSciences，2012，20（5）：695－711.

［21］ Kyung－shik S，Han I.Case－based reasoning supported by genetic algorithms for corporate bond rating ［J］.Expert SystemswithApplications，1999，（16）：85－95.

［22］ Fonseca C M，Fleming P J.An overview of evolutionary algorithms in multiobjective optimization［J］.Evolutionary Computation，1995，3 （1）：165－180.

［23］ Nikolay A Kudryashov.Polynomials in logistic function and solitary waves of nonlinear differential equations ［J］.AppliedMathematicsandComputation，2013，219：9245－9253.

［24］ Humberto Ramos Quoirin，Kenichiro Umezu.The effects of indefinite nonlinear boundary conditions on the structure of the positive solutions set of a logistic equation ［J］.DifferentialEquations，2014，257：3935－3977.