页岩气藏水平井水力压裂裂缝敏感参数数值分析

李玉梅，李军，柳贡慧，2，于丽维，刘明，鹿吉庆

（1.中国石油大学（北京）石油天然气工程学院，北京102249；2.北京信息科技大学，北京100192；3.中国石油新疆油田公司工程技术研究院，新疆 克拉玛依834000；4.天津开发区鑫昌达船舶工程有限公司，天津300457；5.西南石油大学，四川 成都610500）

0 引言

区别于常规气藏开采技术，射孔水平井分段压裂技术已成为低渗透页岩气藏高效开发的有效手段［1］。多级射孔簇可形成多条水力裂缝，从而增加储层形成复杂裂缝网络的几率，获得较高的经济效益。该技术是在同一压裂段内尽可能多地排布人工裂缝，或者减小裂缝间隔距离，大幅增加气藏泄气面积，改善储层与井筒间的流体连通程度，创造较大的储层改造体积［2-3］。大量现场数据显示，约有25%的人工裂缝是无效的。所以，同一压裂段内的裂缝间距以及裂缝条数的优化设计，对有效的储层体积改造至关重要［4］。

页岩气储集层的地质和力学特征与常规天然气储集层有较大差别。页岩的层理结构。导致平行于层理面和垂直于层理面的力学特性具有较强的各向异性。传统的分段压裂理论模型和压裂造缝机理，并不适用于指导低孔、低渗且非均质性较强的页岩气井压裂设计，而数值模拟方法因其具有不受外界条件影响且可进行重复性计算等特点，被许多国内外学者用来替代室内试验手段，对分段压裂缝间距进行优化设计［5-8］。本文基于页岩弹性各向异性特征和渗流与变形耦合理论模型，建立了水平井分段压裂非平面水力裂缝扩展的三维有限元数值模型，开展了水平井压裂方式以及页岩力学特性对分段压裂缝间干扰机理的研究分析，为探索层理性页岩气储集层压裂造缝机理以及分段压裂优化设计提供了有效的指导意见。

1 理论基础

1.1 不同压裂方式的复合应力场

水平井分段压裂过程中，裂缝会从各个射孔簇处起裂并延伸，每条裂缝的张开都会挤压裂缝两边的地层，形成诱导应力。多条裂缝间的相互干扰又促使形成更为复杂的网状裂缝。要达到最好的体积压裂效果，一般采用沿着最小水平主应力方向，形成的裂缝垂直于井筒轴线的横切裂缝［9-10］。

先压裂缝产生后，将导致裂缝周围一定区域内的应力分布发生改变［11］，水平主应力差值在距裂缝壁面一定范围内会大幅减小，因而也将影响后续压裂水力裂缝的起裂［12-13］。常规压裂通常是从井筒趾部开始，依次向跟部压裂，第3 条裂缝在先压的2 条主裂缝之后形成，这种压裂方式为顺序压裂法（见图1a）。区别于常规压裂工艺，在选择压裂方式中，第3 条裂缝形成于先压的2 条主裂缝的中间位置，位置和压裂顺序的不同将引起复合应力场的改变（见图1b）。由此可见，压裂裂缝的顺序和位置可以人为控制，从而改变复合应力产生，导致不同的压裂效果。无论是顺序压裂还是选择压裂方式，压裂工艺的不同会导致不同的应力转向状态，从而影响缝间距的选择。

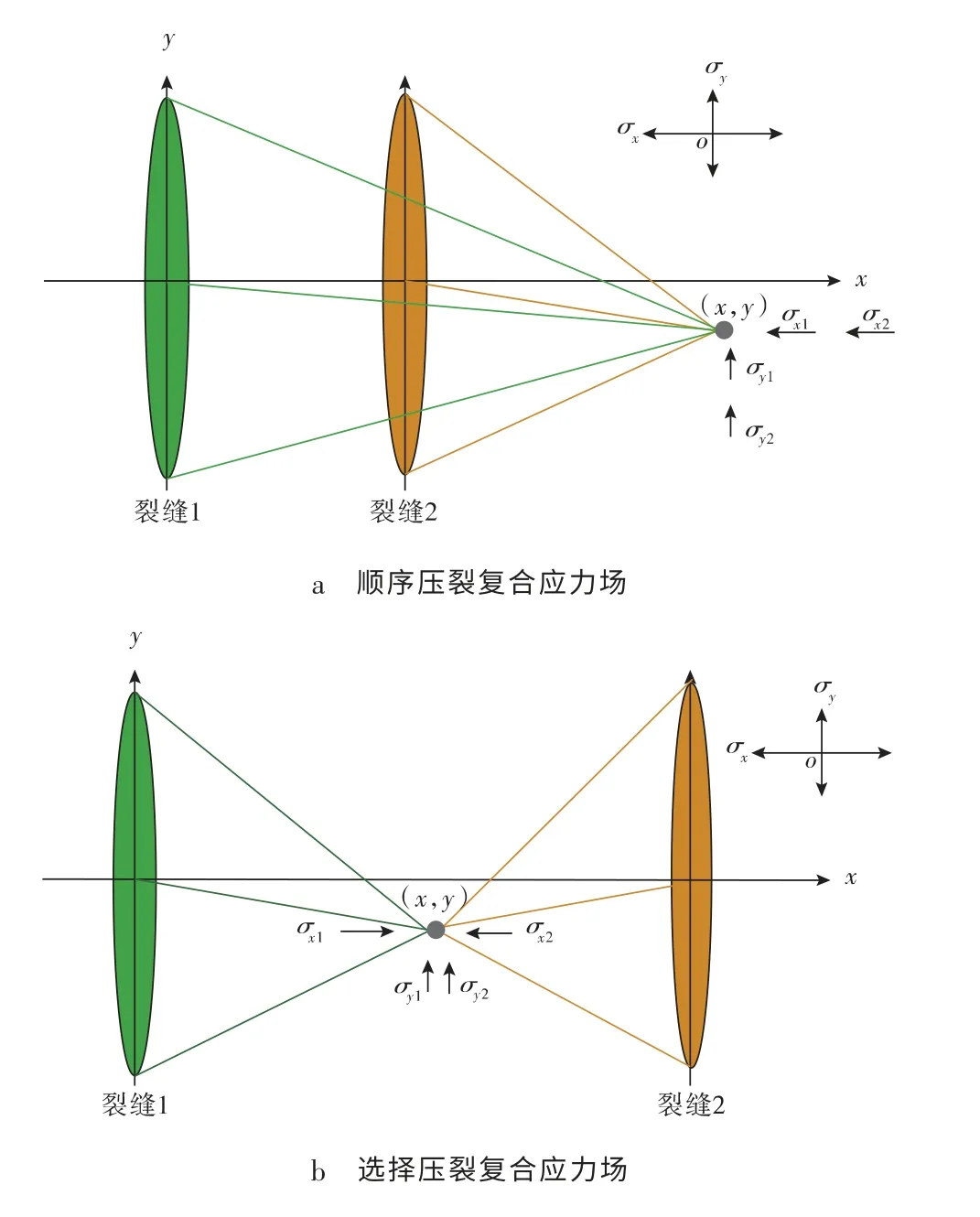
图1 不同压裂方式的复合应力场

1.2 各向异性弹性变形理论模型

层理性地层是各向异性地层中最简单的形式，工程上通常将页岩看作是层理性地层的典型。页岩在层理面的应力-应变特征是各向同性，可用5 个独立的弹性常数来描述。虎克定律反映了弹性体中应力与应变的线弹性关系，对于各向异性材料，其应力-应变本构方程可以表示为

其中

Eh=Ex=Ez，νh=νxz，Eh，νh分别表示平行于各向同性面的弹性模量和泊松比。EV=Ey，νV=νyz＝νxy，EV，νV分别表示垂直于各向同性面的弹性模量和泊松比。各向同性面XOZ 内的剪切模量为

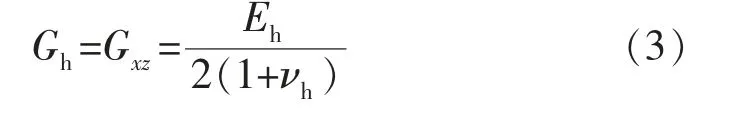
Batugin 等［14］提出垂直于各向同性面的YOZ 面和XOY 面的第5 个弹性常数，即GV＝Gyz＝Gxy的数学解法，并通过大量的实验数据对其进行了验证。

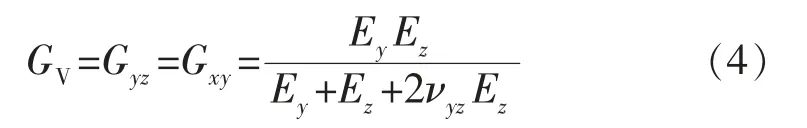
2 数值分析

2.1 局部坐标系设置

考虑层理性页岩的横向各向同性特征，建立数值模型之后需要建立材料的局部坐标系，所建模型坐标系如图2所示。模型全局坐标为XYZ，各向同性面为XOZ，对称轴为Y 轴。水平井沿最小水平主应力方向（σh）钻进，人工水力裂缝缝长沿着最大水平主应力方向（σH），缝高沿垂向Z 轴方向贯穿整个储层。层理面局部坐标系为X′Y′Z′，局部坐标系和全局坐标系的三轴一一对应，即X-X′，Y-Y′，Z-Z′。裂缝形态以半无限模型为例，计算中预置裂缝缝长Lf、缝宽Wf、缝高hf，缝间距为S，图3为所建裂缝几何参数示意。

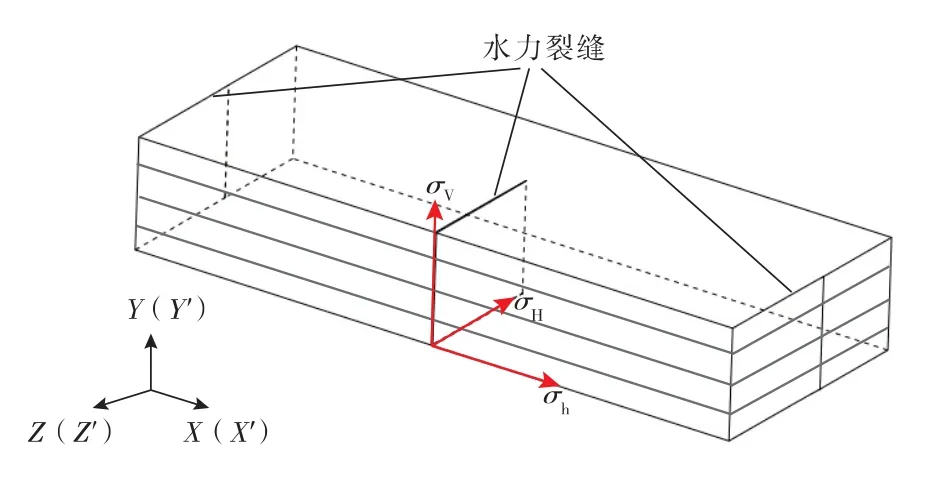
图2 坐标系示意

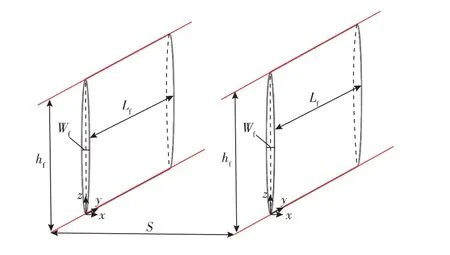
图3 裂缝几何参数示意

2.2 有限元模型及力学参数

基于页岩弹性各向异性特征和渗流与变形耦合理论模型，利用有限元数值计算软件Abaqus，建立了水平井分段压裂非平面水力裂缝扩展三维有限元数值模型（见图4）。

图4 有限元数值模型建立过程

水力裂缝沿水平井筒平行排布，裂缝嵌入模型内部，缝高即储层厚度。采用位移和孔压耦合六面体单元C3D8P 对数值模型进行网格划分，并对裂缝尖端进行细化处理。

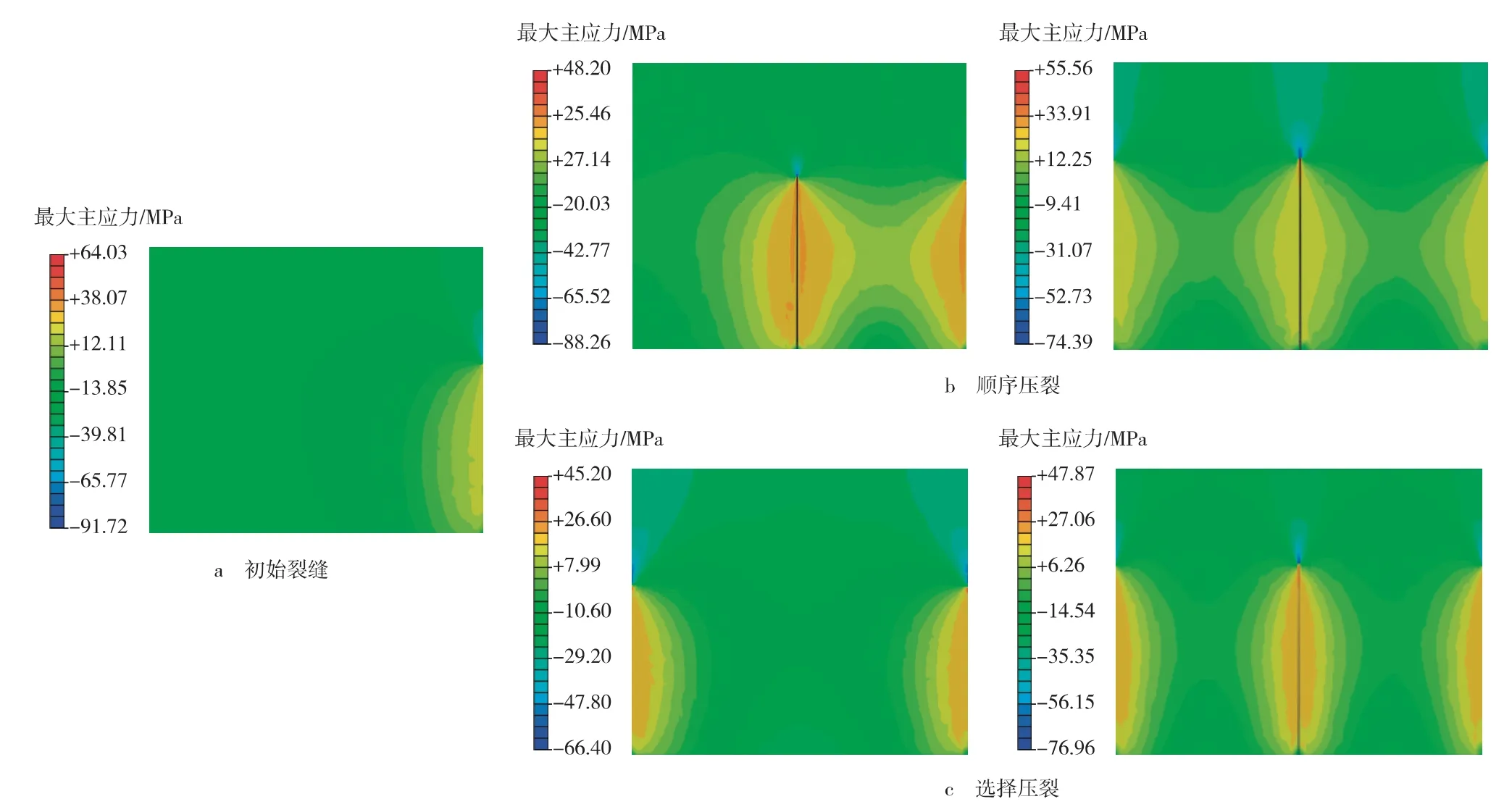
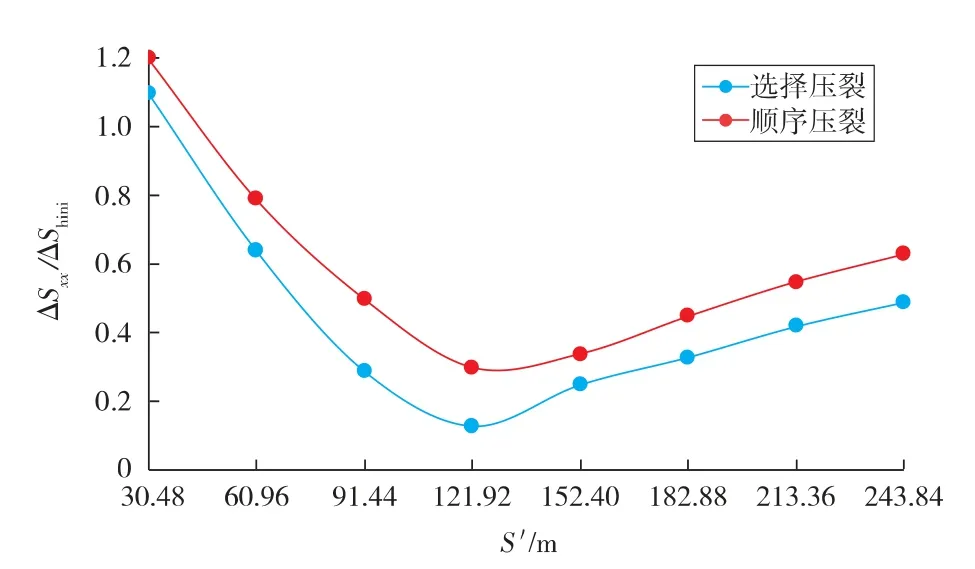
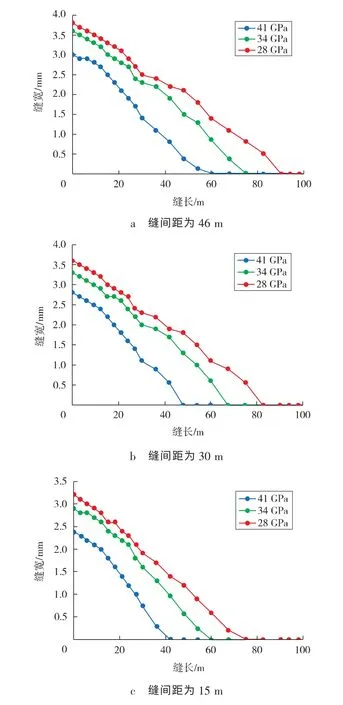
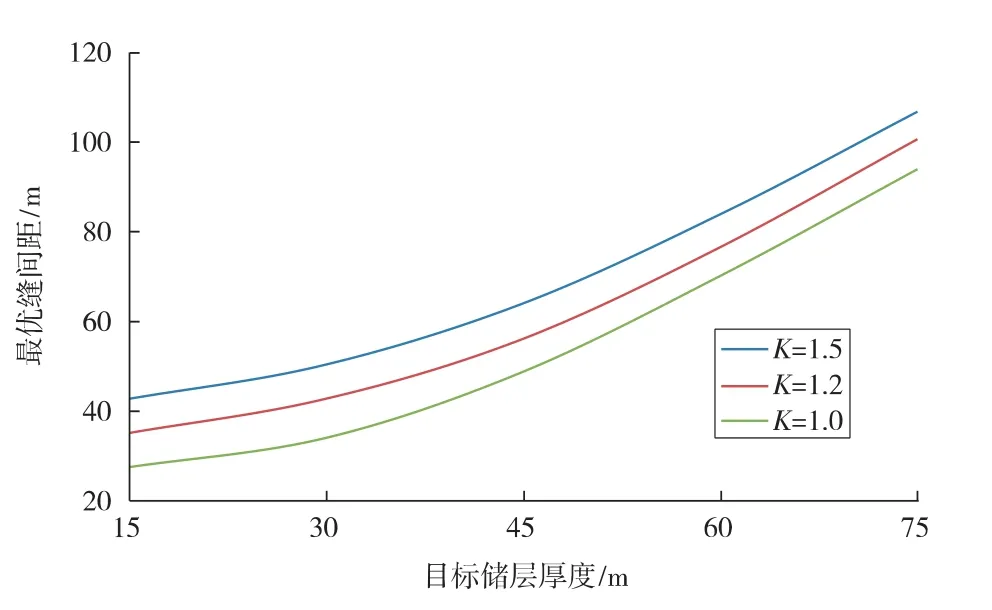
网格划分后，在初始条件设置中，为所有单元节点赋值饱和度为1，地层流体渗透率为0.000 1×10-3μm2，孔隙比为3%，初始孔隙压力为16 MPa。层状岩体处理成横向各向同性介质，描述这种性状的岩石应力-应变关系可以采用5 个独立的弹性常数。垂直于各向同性面的弹性模量和泊松比取定值，分别为EV=30.61 GPa，νV=0.223；平行于各向同性面的弹性模量和泊松比的取值范围分别为36.65 GPa

材料参数设定后，将材料的横向各向同性赋予局部坐标系。地层岩石抗拉强度为2 MPa，流体密度为1.0 g/cm3，最大水平主应力为29 MPa，最小水平主应力为24 MPa，垂直地应力为40 MPa，地层初始孔隙压力为16 MPa。边界条件设置过程中，对模型外侧边界施加位移约束和孔隙压力，在裂缝内表面单元施加净压力和孔隙压力。

3 结果分析

3.1 压裂方式对裂缝间距的影响

对于水平井分段压裂，目前的压裂方式主要有顺序压裂和选择压裂（德克萨斯州两步压裂法）。图5为初始裂缝形成后，“中间裂缝” 的加入对2 种压裂方式下诱导应力场的影响。随着裂缝的延伸，应力干扰区扩展，最后彼此叠加。对于顺序压裂方式，初始2 条裂缝的间距相对较小，产生的缝间诱导应力较大，不利于裂缝延伸。与顺序压裂方式相比，选择压裂方式形成的初始裂缝间距足够大，诱导应力干扰叠加区域较小，促使“中间裂缝”在初始形成裂缝间顺利扩展延伸。

图5 不同压裂方式对应诱导应力云图

不同压裂方式下，“中间裂缝” 加入后，诱导应力ΔSxx（垂直裂缝方向）与初始水平应力差ΔShini的无量纲之比和缝间距的关系如图6所示。研究发现，相比顺序压裂方式，选择压裂方式在“中间裂缝”加入后，产生的诱导应力较小。外缘裂缝间距S′＝2S=137.16 m 时，顺序压裂产生诱导应力，出现最小值；当外缘裂缝间距为121.92 m 时，选择压裂产生诱导应力，出现最小值。由此可见，选择压裂方式下的最优缝间距要小于顺序压裂方式。

图6 “中间裂缝”加入后的最优裂缝间距

3.2 力学特性对裂缝扩展形态的影响

图7为射孔簇间距为46，30，15 m 条件下，目标储层弹性模量对裂缝形态的影响规律。研究发现，弹性模量和射孔簇间距对裂缝扩展形态均有较大影响。较高的弹性模量会引起较强的缝间干扰，导致缝宽、缝长均减小，那么对于高弹性模量地层，需增加簇间距，减小分缝间干扰。较大的缝间距缝间干扰较小，缝宽、缝长也随之增加；反之，缝间距较小，缝宽、缝长均有所减小，限制了裂缝扩展延伸。另外，工程上可以通过提高泵速和降低钻井液黏度保证裂缝进一步扩展延伸。

定义页岩层理面弹性模量与层理面法向弹性模量的比值K=Eh/EV。K 是表征页岩弹性各向异性度的参考值，其值越小，表示弹性各向异性度越高。图8为不同储层厚度条件下，弹性模量各向异性对最优缝间距的敏感性影响分析曲线。研究发现：较高的弹性模量各向异性导致较大的最优缝间距；反之，较小的弹性模量各向异性导致较小的最优缝间距。弹性模量各向异性从1.5 变化到1.2 时，最优缝间距变化了大约7.62 m。可见，页岩的弹性模量以及弹性模量各向异性对缝间距有较大影响，因此考虑页岩的岩石力学特性对缝间距的优化选择至关重要。

图7 目标储层弹性模量对裂缝扩展形态的影响

图8 弹性模量各向异性对最优缝间距的影响

4 结论

1）相比顺序压裂方式，选择压裂方式充分利用了诱导应力的作用，形成的初始裂缝间距足够大，诱导应力干扰叠加区较小，最优缝间距也较小，有利于更多的“中间裂缝”扩展延伸。

2）较高的弹性模量会引起较强的缝间干扰，导致缝宽和缝长均减小，那么对于高弹性模量地层，需增加射孔簇间距，减小缝间干扰。

3）弹性模量各向异性越大，最优缝间距越大。因此，考虑页岩的弹性各向异性力学特性对缝间距的优化选择至关重要。

［1］王益维，张士诚，李宗田，等.深层低渗透储层压裂裂缝处理技术［J］.特种油气藏，2010，17（3）：87-89.

［2］Lolon E P，Cipolla C L，Weijers L，et al.Evaluating horizontal well placement and hydraulic fracture spacing/conductivity in the Bakken Formation，North Dakota［R］.SPE 124905，2009.

［3］周洪亮，尹洪军，李美芳，等.各向异性油藏水平井井网渗流场分析［J］.特种油气藏，2010，17（1）：81-84.

［4］Wei Y，Economides M J.Transverse fractures from a horizontal well［R］.SPE 94671，2005.

［5］Manchanda R，Sharma M M.Impact of completion design on fracture complexity in horizontal wells［R］.SPE 159899，2012.

［6］Olson J E.Multi-fracture propagation modeling：Applications to hydraulic fracturing in shales and tight gas sands［R］.ARMA 08-327，2008.

［7］Wu R，Kresse O，Weng X，et al.Modeling of interaction of hydraulic fractures in complexfracture networks ［R］.SPE 152052，2012.

［8］Meyer B，Bazan L W，Jacot R H，et al.Optimization of multiple transverse hydraulic fractures in horizontal wellbores ［R］.SPE 131732，2010.

［9］郭天魁，张士诚，刘卫来，等.页岩储层射孔水平井分段压裂的起裂压力［J］.天然气工业，2013，33（12）：87-93.

［10］刘洪，胡永全，赵金洲，等.重复压裂气井诱导应力场模拟研究［J］.岩石力学与工程学报，2004，23（23）：4022-4027.

［11］吕志凯，何顺利，黄摇伟，等.水平井分段压裂总应力场计算模型［J］.大庆石油地质与开发，2012，31（2）：120-124.

［12］Palmer I D.Induced stresses due to proposed hydraulic fracture in coalbed methane wells［C］//the SPE Rocky Mountain Regional/Low Permeability Reservoirs Symposium，Denver，1993.

［13］徐严波.多条裂缝同时延伸时裂缝几何尺寸影响因素［J］.大庆石油地质与开发，2009，28（3）：89-92.

［14］Batugin S A，Nirenburg R K.Approximate relation between the elastic constants of anisotropic rocks and the anisotropy parameters ［J］.Journal of Mining Science，1972，8（1）：5-9.