利用压汞资料计算复杂断块油藏油水相对渗透率曲线
桑丹,姚约东,周练武,李泉凤,任瑞川
(1.中国石油大学(北京)石油工程教育部重点实验室,北京102249;2.中国石油大港油田公司采油一厂,天津300280)
1 相对渗透率曲线的获取
油水相对渗透率曲线是油藏工程和油藏数值模拟研究的基础[1]。获取油水相对渗透率一般是在室内岩心实验的基础上,运用稳态或非稳态的方法进行测量[2],但这种方法存在取心污染、 测量误差和无法反映油藏整体状况等问题。前人提出了一些采用动态数据计算相对渗透率曲线的方法,如水驱曲线法[3]和含水率曲线法[4],这些方法可以较好地反映油藏整体动态变化,但对于非均质较强的复杂断块油藏,同一油藏内可能存在多套油水渗流规律,因此,尽可能多收集油藏油水相渗资料,建立反映油藏非均质渗流特征的相渗资料库,对于油藏工程和数值模拟研究是很有必要的。
本文应用分形理论、Purcell 润湿相相对渗透率计算公式和Burdine 非润湿相相渗曲线计算公式,结合压汞毛细管力曲线,推导计算出多条油水两相相对渗透率曲线,根据物性综合指数将相对渗透率曲线进行分类,并根据复杂断块油藏平面、纵向上的非均质物性特征,选用对应类型的相对渗透率曲线(见图1)。
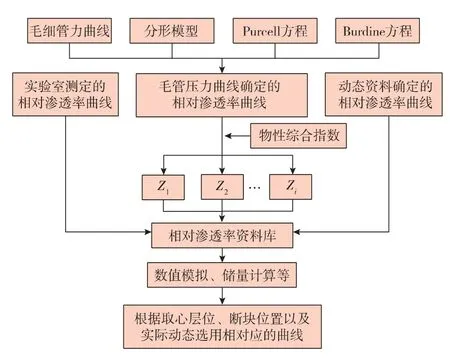
图1 复杂断块油藏相对渗透率曲线的获取
2 油水相对渗透率曲线计算
压汞实验是在一定的压力下,将汞压入多孔介质的微观孔隙中得到压力与汞体积关系的实验。由于毛细管力的存在,在一定压力下,汞只能进入孔喉半径大于该压力对应的孔喉半径的孔隙中,从而可用压汞数据研究多孔介质复杂的微观孔隙结构特征[5]。
根据分形几何原理[6],若储层孔径分布符合分形结构,则储层中孔径大于r 的孔隙数目N(r)与r 的幂函数关系为

式中:rmax为储层中最大孔隙半径,μm;P(r)为孔径分布密度函数;C 为比例常数;Df为孔隙分形维数。
式(1)对r 求导,可得到P(r)的表达式:
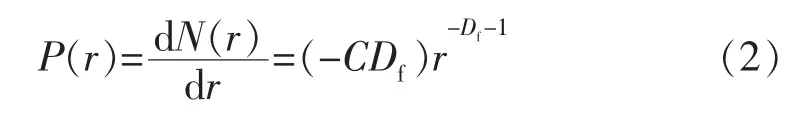
则储层中孔径小于r 的孔隙累积体积V(r)的表达式为

式中:α 为与孔隙形状相关的常数,如孔隙为立方体,则α=1,若孔隙为球体,α=4π/3;rmin为储层中最小孔隙半径,μm。
储层的总孔隙体积V 为
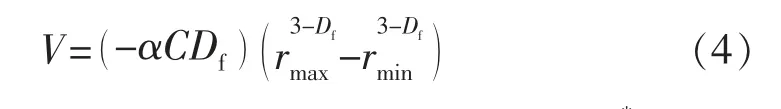
可得到孔径小于r 的累积孔隙体积分数S*w(即归一化润湿相饱和度)的表达式:
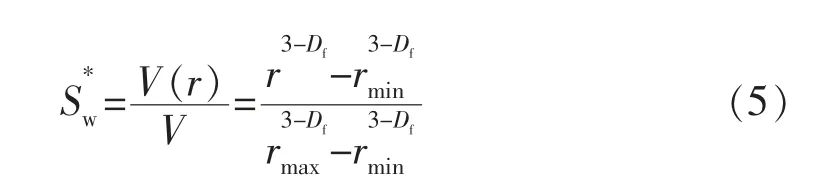
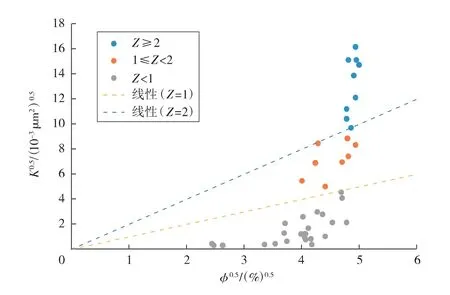
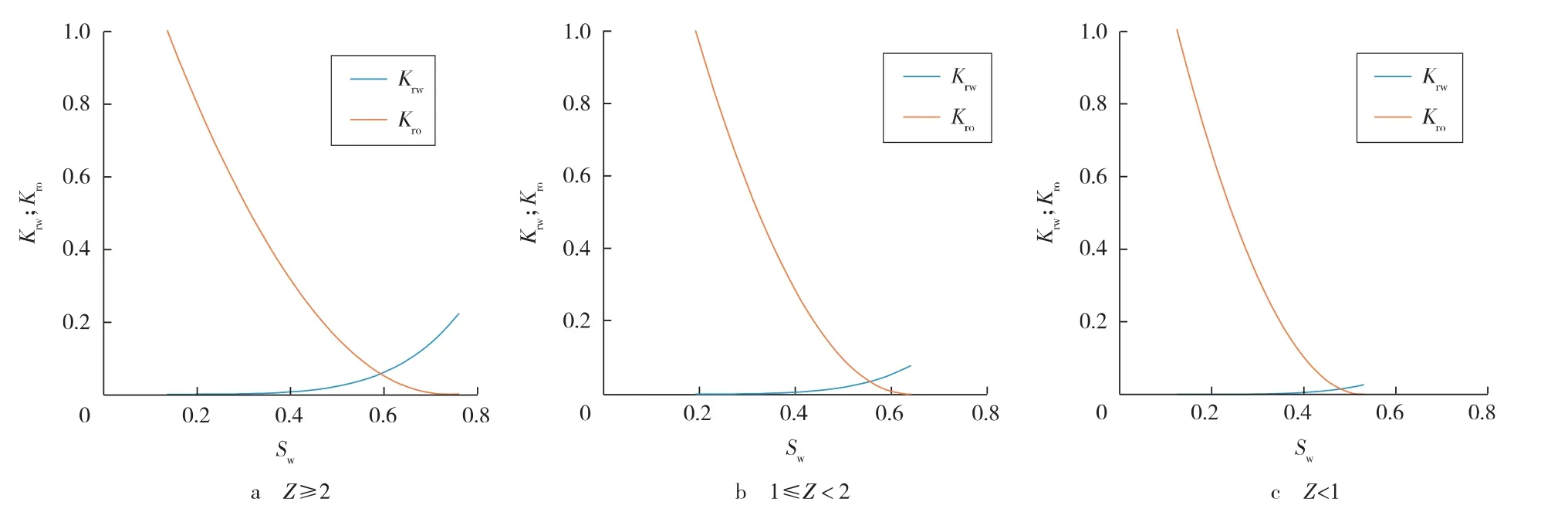
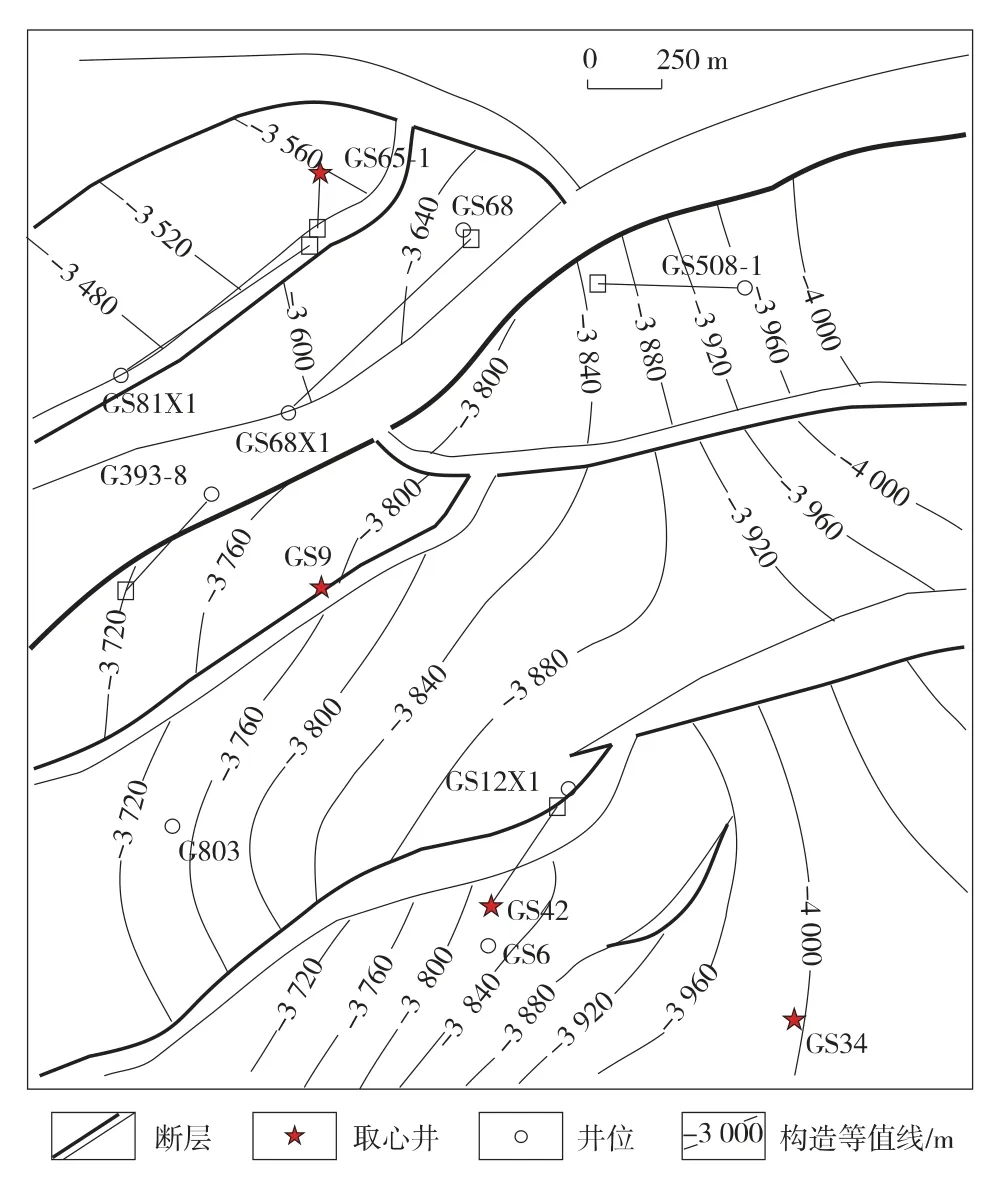
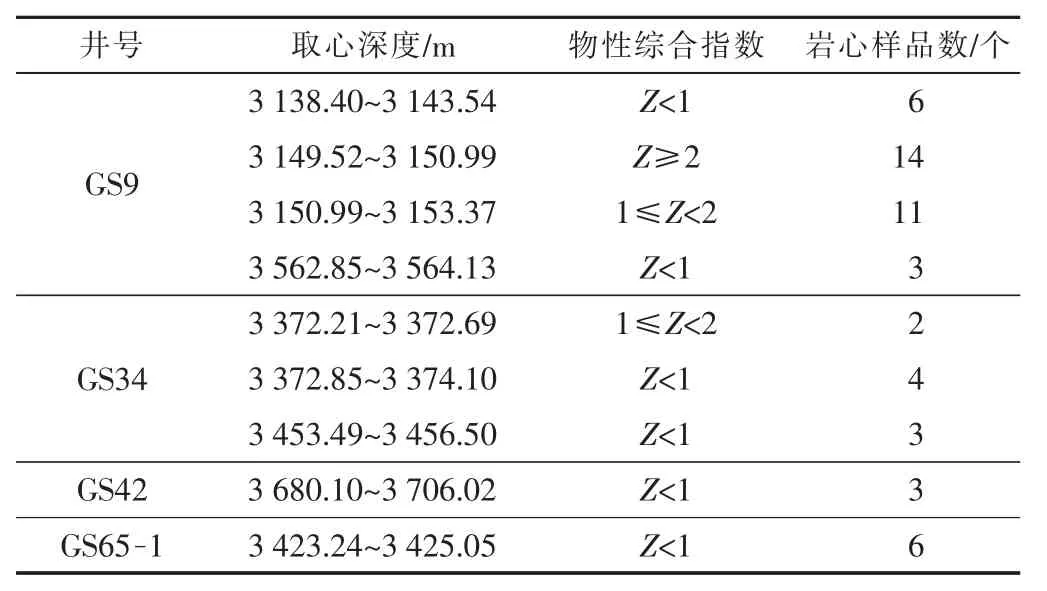
由于rmin< 毛细管压力的计算公式为 将式(7)代入式(6)得 式中:pmin为储层中最大孔径rmax对应的毛细管压力,即入口毛细管压力,MPa。 式(8)为毛管压力曲线的分形几何公式,该模型即为经典的Brooks-Corey 模型[7],它修正了Corey 模型中排驱型毛细管压力与饱和度的关系。 利用毛细管压力曲线数据推导相对渗透率曲线的方 法 主 要 有2 种:Purcell 方 法[8]和Burdine 方 法[9]。2005年,Li 和Horne[10]通过实验对比了这2 种方法,发现Purcell 模型对润湿相无论是驱替或吸渗过程的相渗曲线都能拟合得很好,但对非润湿相拟合效果一般;Burdine 模型更加适用于拟合非润湿相的相对渗透率曲线。因此,可利用Purcell 模型推导计算润湿相的相渗曲线,用Burdine 模型推导计算非润湿相的相渗曲线。 Purcell 提出的润湿相相对渗透率计算公式: Burdine 提出的改进的相渗曲线计算公式: 式中:Krw为润湿相相对渗透率;Krnw为非润湿相相对渗透率;Sw为润湿相饱和度;Swr为残余润湿相饱和度;Snwi为非润湿相初始饱和度。 将式(8)代入式(9),并进行Sw对S*w 的积分变换得 同理,将式(8)代入式(10),可以推导得 根据式(8)可得出由压汞毛管力曲线确定的多孔介质微观孔喉分布的分形维数,进而由式(11)、(12)确定不同毛管压力曲线对应的油水相渗曲线。 应用此方法结合大港唐家河油田沙一下段52 个岩样的压汞曲线进行了实例计算,得到的孔隙分形维数Df为2.187~2.895,并根据Df结合相对渗透率计算公式,得出52 条油水相对渗透率曲线,引入物性综合指数Z 对岩样进行分类[11-12]。物性综合指数Z 是评价储层单位孔隙度能提供的渗流能力的指标,对于砂岩储层根据各岩样的物性综合指数Z,将岩样分为Z≥2,1≤Z<2,Z<1 三类,如图2和表1所示。将各类岩样对应的油水相渗曲线进行归一化处理[13],结果见图3。 图2 唐家河油田岩心孔隙度与渗透率关系 表1 物性综合指数分类 图3 不同物性综合指数对应的归一化相渗曲线 由物性综合指数分类的结果可以看出:1)Z≥2 的岩样对应的油水相对渗透率曲线呈上凹型,等渗点大于0.5,油相、水相端点相对渗透率高,孔隙度和渗透率相对较大,储层孔隙发育,连通性好,属于中孔、中高渗亲水储层。2)1≤Z<2 的岩样残余油饱和度高,随含水饱和度增加,油相相对渗透率缓慢下降;水相相对渗透率在低含水饱和度时较为平缓,随着含水饱和度的增加,上升幅度增大,最终水相相对渗透率在0.1~0.2 左右,属于中低孔、中低渗储层。3)Z<1 的岩样油水两相共渗区范围窄,驱油效率低,随着含水饱和度的增加,油相相对渗透率急剧下降,而水相相对渗透率却升不起来,呈直线型,孔隙度和渗透率较小,连通性差,属于低孔、低渗储层[14-16]。3 类相渗资料中,Z<1 的岩样数占总比例的50%,综上分析可知,唐家河沙一下段为以低孔、低渗为主的非均质储层。 由沙一下取心井构造位置关系(见图4)及岩心物性分类(见表2)可知,唐家河油田沙一下储层的空间非均质性差异很大,储层的平面非均质性要弱于层间和层内,具体表现在:取心深度越深,物性综合指数越低,储层单位孔隙度能提供的渗流能力越差;中部断块(GS9 井附近)物性明显好于边部断块(GS34,GS42,GS65-1)的物性。唐家河油田沙一下段储层主要为重力流水道浊积砂体沉积,沉积规模小,岩性稍粗,砂体连续性相对较差,沉积微相带主要影响开发初期储层非均质性。随着注水开发进行,非均质性变得复杂,注水开发导致的不同沉积微相带非均质变化不一:岩性、物性好的储层水洗程度高,含油性变差;而岩性、物性差的储层人工注水波及程度低,油气动用程度低,从而拉大了优劣储层的差距,加剧了储层非均质性。在可采储量估算及精细油藏数值模拟中,应充分考虑平面、纵向上非均质特点。纵向上,根据物性变化选取不同物性综合指数对应的油水相渗曲线;平面上,根据各断块的物性分布选取对应的油水相渗曲线。 图4 唐家河沙一下段底界构造示意 表2 唐家河油田取心层位及岩心物性分类 1)复杂断块油藏油水相渗曲线形态复杂,可根据物性综合指数Z 分为3 类。其中,Z≥2 为孔隙连通性较好的中孔、中高渗亲水储层,1≤Z<2 为中低孔、中低渗储层,Z<1 为渗流能力差的低孔、低渗储层。 2)结合分形理论、Purcell 及Burdine 相对渗透率公式计算油水相对渗透率曲线,根据储层物性综合指数分类,并分层、分区块选用对应的相渗曲线进行油藏工程和精细数值模拟研究,所得到的相对渗透率曲线具有代表性,能够真实反映复杂断块油藏非均质渗流特征。 3)对于缺少相渗资料且无法借鉴其他油藏相渗资料的复杂断块油藏,可以通过该方法进行相渗资料的补充。 [1]高文君,姚江荣,公学成,等.水驱油田油水相对渗透率曲线研究[J].新疆石油地质,2014,35(5):552-557. [2]陈忠,殷宜平,陈浩.非稳态法计算油水相对渗透率的方法探讨[J].断块油气田,2005,12(1):41-43. [3]杜殿发,林新宇,巴忠臣,等.利用甲型水驱特征曲线计算相对渗透率曲线[J].特种油气藏,2013,20(5):93-96. [4]王怒涛,陈浩,王陶,等.用生产数据计算油藏相对渗透率曲线[J].西南石油学院学报,2005,27(5):26-29. [5]李留仁,赵艳艳,李忠兴,等.多孔介质微观孔隙结构分形特征及分形系数的意义[J].石油大学学报:自然科学版,2004,28(3):105-107. [6]贺承祖,华明琪.微观孔隙结构分形特征及分形系数的意义[J].石油与天然气地质,1998,19(1):15-23. [7]Brooks R H,Corey A T.Hydraulic properties of porous media [D].Fort Collins:Colorado State University,1964:3-27. [8]Purcell W R.Capillary pressures-their measurement using mercury and thecalculationofpermeability[J].Trans.AIMME,1949,186(2):39-48. [9]Burdine N T.Relative permeability calculation from size distribution data [J].Journal of Petroleum Technology,1953,5(3):71-78. [10]Li K,Horne R N.Comparison of methods to calculate relative permeability from capillary pressure in consolidated water-wet porous media [J].Water Resources Research,2006,42(6):285-293. [11]郭振华,李光辉,吴蕾,等.碳酸盐岩储层孔隙结构评价方法:以土库曼斯坦阿姆河右岸气田为例[J].石油学报,2011,32(3):459-465. [12]文华,孙娜.一种定量描述气藏储层非均质性的新方法[J].特种油气藏,2011,18(1):51-53. [13]缪飞飞,刘小鸿,张宏友,等.相对渗透率曲线标准化方法评价[J].断块油气田,2013,20(6):759-762. [14]杨少春,王瑞丽.不同开发时期砂岩油藏储层非均质三维模型特征[J].石油与天然气地质,2006,27(5):652-658. [15]何建民.油水相对渗透率曲线异常影响因素探讨[J].油气地质与采收率,2009,16(2):74-76. [16]张学文,尹家宏.低渗透砂岩油藏油水相对渗透率曲线特征[J].特种油气藏,1999,6(2):27-31.

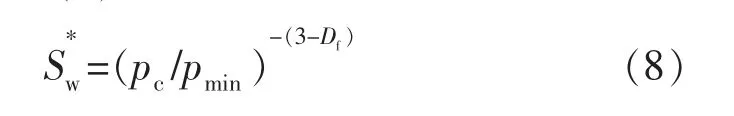
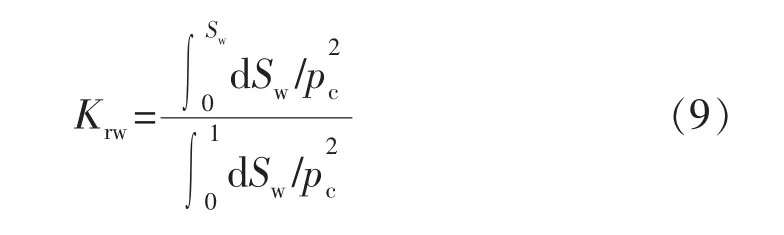
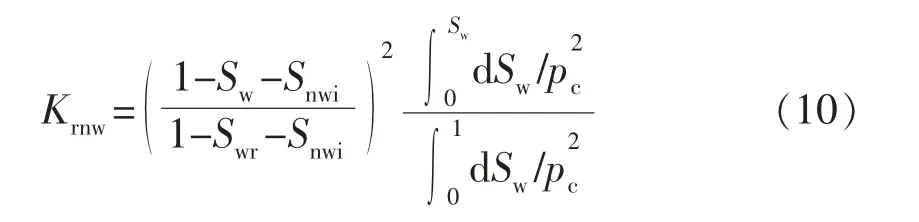

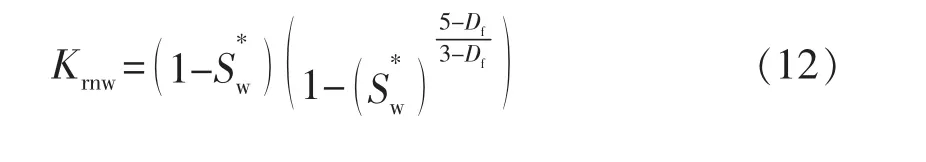
3 复杂断块油藏相对渗透率曲线分类

4 分区块、分层位应用相对渗透率曲线
5 结论

