考虑分子扩散作用的裂缝性油藏CO2 混相驱数值模拟

丁志文，董平川，杨新影，丁道权，左文永，潘红霞

（1.中国石油大学（北京）石油工程教育部重点实验室，北京102249；2.中国石油塔里木油田公司勘探开发研究院，新疆 库尔勒841000；3.中国石化中原油田分公司石油化工总厂，河南 濮阳457061）

1 研究现状

在裂缝性油藏开发中，CO2混相驱是提高采收率的有效手段，注入的混相气体通过重力排驱、毛细管驱动、分子扩散等作用，实现裂缝与基质岩块之间的交叉流和传质作用，达到驱替基岩中残留油的目的［1-2］。国外开展注气开发提高采收率的时间较早，无论是室内实验技术还是数值模拟技术，都相对成熟，但是在裂缝性储层注气室内实验研究中，往往忽略多孔介质对流体相态的影响。双孔介质中，气驱数值模拟方法考虑的驱替机理不够全面，常常假定条件过多而忽略某些重要机理，因此适用性有限［2］。

我国对CO2提高采收率方法的研究还处于起步阶段，不少学者对CO2混相驱的数值模拟进行了相关研究。苏玉亮等［3］针对低渗油藏，建立了考虑吸附现象的CO2混相驱油数学模型，并模拟了CO2混相驱油过程；孙晓旭等［4］应用数值模拟软件，用正五点法单元井网，对华北任丘潜山油藏CO2驱注气参数进行了优化；宋道万［5］利用概念模型和实际油藏模型，分析了胜利油区某低渗油藏CO2混相驱的影响因素。但上述研究没有考虑分子扩散作用对CO2混相驱的影响。李南等［6］建立了低渗透油藏CO2混相驱过程中考虑对流扩散的流固耦合模型，但此模型对裂缝性双重介质油藏并不适用；文玉莲［2］建立了考虑分子扩散行为影响的双重介质黑油模型，但该模型不能精确描述多组分渗流规律。在裂缝性油藏CO2混相驱过程中，分析多组分相态变化条件下的分子扩散作用对混相驱效果及波及面积的影响具有重要意义，但目前国内并没有将考虑分子扩散和多组分、多形态模拟很好地统一起来。

本文针对裂缝性油藏CO2混相驱的研究现状，在室内实验的基础上，建立了考虑分子扩散作用的描述裂缝性油藏CO2混相驱渗流规律的多相、 多组分数学模型。

2 基本流动方程

假设：油藏中的渗流为多相、多组分（流体含有Nc个油组分和Nc个气组分）等温渗流，服从达西定律；油水之间不互溶，且油藏中油气两相瞬时达到相平衡状态；忽略毛细管力；裂缝与裂缝、裂缝与基质，以及基质与基质之间均可进行流体交换，即为双孔双渗模型。

2.1 运动方程

根据达西定律，流体在基质和裂缝系统中的渗流速度为

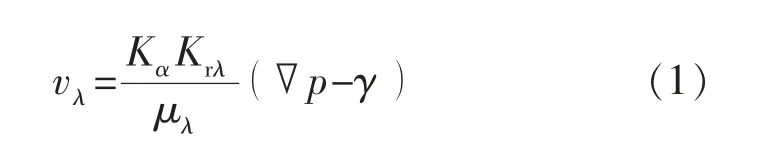
其中 γ＝ρλg

式中：vλ为流体的渗流速度，cm/s；Kα为多孔介质的渗透率，10－3μm2；Krλ为流体在介质中的相对渗透率；μλ为流体的黏度，mPa·s；▽p 为压力梯度，MPa/m；ρλ为流体的密度，g/cm3；g 为重力加速度，取值为9.8 m/s2。

2.2 分子扩散方程

扩散作用是流体在多孔介质中的一种重要质量传递机制，一般分为分子扩散、Knudsen 扩散和表面扩散。当多孔介质的孔隙直径较小，与气体分子的平均自由程接近时（Knudsen 数远远小于1），分子对孔壁的碰撞较分子之间的相互碰撞占主导地位，是引起沿孔隙扩散阻力的主要因素，此时的扩散为Knudsen 扩散。这类扩散作用在煤层气和页岩气中应用较为广泛［7-8］。表面扩散用来描述扩散物质被固体吸附行为，分子直径大小对其影响微弱，主要取决于流体的化学性质。分子扩散描述的是，当气体分子的平均自由程小于孔隙直径时（Knudsen 数小于1），扩散阻力主要取决于分子间的相互碰撞，流体中某些组分分布不均匀，在空间形成浓度差，从而引起质量传递。

本文针对的是裂缝性油藏，忽略岩石表面对流体组分的吸附，认为扩散为分子扩散，扩散通量由费克定律描述［9-11］，则流体在单位时间内，组分i 通过单位截面的摩尔扩散量为

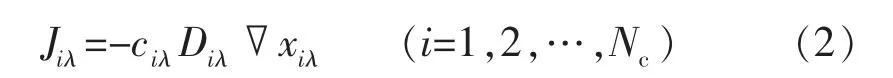
则相λ 在单位时间内，组分i 通过单位截面的质量扩散量为

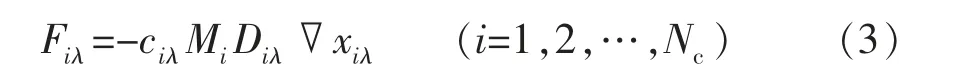
式中：ciλ为组分i 在相λ 中的浓度，mol/mL；Jiλ为组分i在相λ 中的摩尔扩散量，mol/（s·cm2）；Diλ为组分i 在相λ 中的扩散系数，cm2/s；xiλ为组分i 在相λ 中的摩尔分数；Mi为组分i 的摩尔质量，g/mol；Fiλ为组分i 在相λ 中的质量扩散量，g/（s·cm2）。

分子扩散系数是关于油藏温度、压力、流体性质的函数，一般特定油藏的扩散系数由实验测定，而多组分油气系统的扩散系数经实验测定较为困难，本文扩散系数的设定参考文献［11］。

2.3 连续性方程

2.3.1 基质连续性方程

组分i 在基质中的连续性方程为

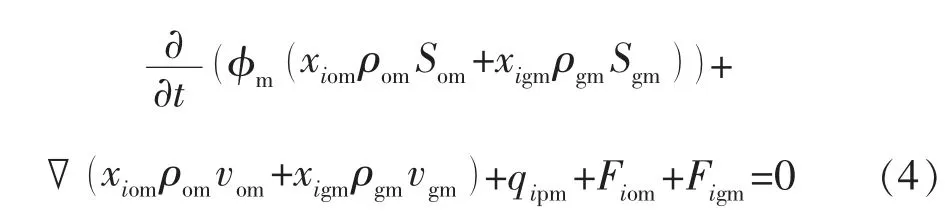
其中，qipm表示组分i 的窜流量［12］：

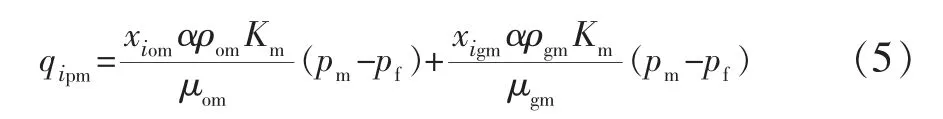
式中：φm为基质的孔隙度；So，Sg分别为含油饱和度、含气饱和度；xiom，xigm分别为组分i 在油相和气相中的摩尔分数；α 为形状因子，m-2；pm，pf分别为基质、 裂缝压力，MPa；Lx，Ly，Lz分别为基质岩块在X，Y 和Z 方向的尺寸大小，m。

2.3.2 裂缝连续性方程

组分i在裂缝中的连续性方程为

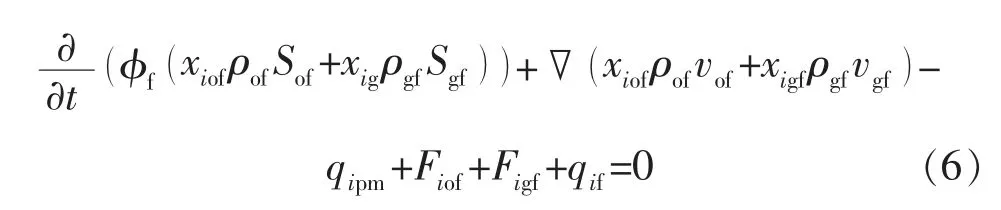
表示单位时间、单位油藏体积采出或注入的组分i的质量流量为

式中：qo，qg分别为单位时间、 单位油藏体积采出或注入的油、气质量流量，g/（s·cm3）。

2.4 约束条件

相平衡（逸度）方程约束条件：

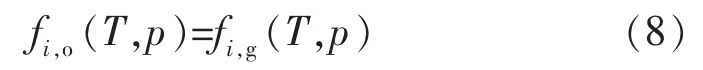
各相饱和度和摩尔分数满足归一化条件：

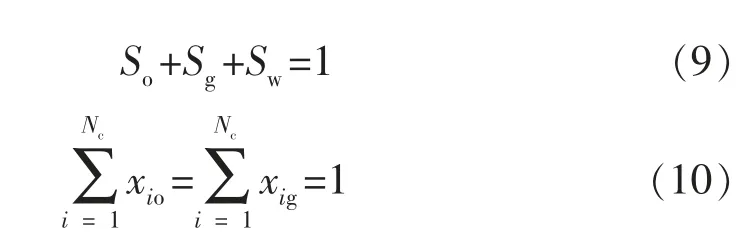
初始条件：

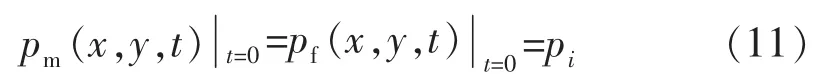
边界条件：假设外边界Γ1为封闭边界，而内边界Γ2为定压边界，则

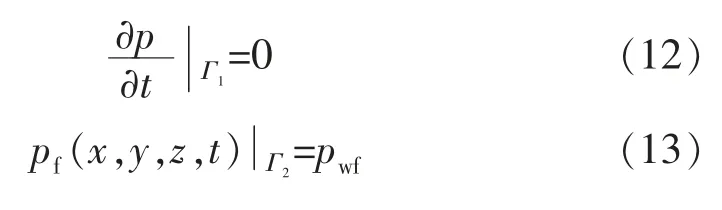
3 数值求解实例分析

将式（1）、式（3）和式（5）代入式（4），可得基质渗流微分方程：

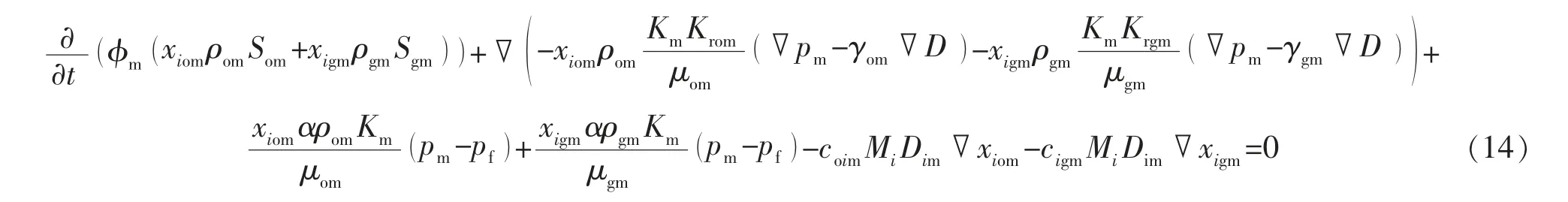
将式（1）、式（3）、式（5）和式（7）代入式（6），可得裂缝渗流微分方程：

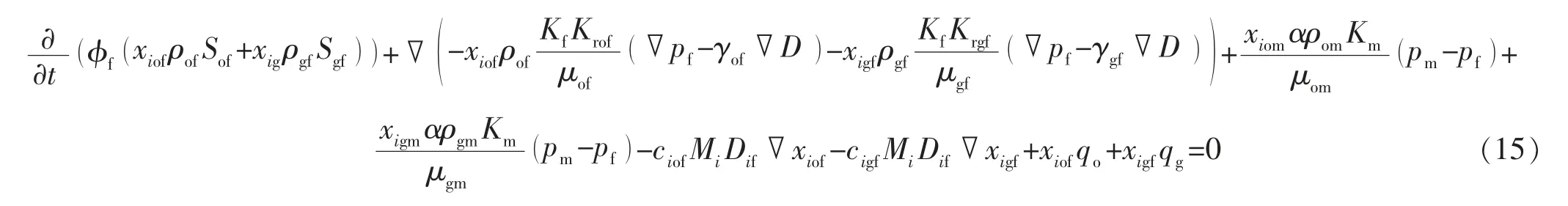
偏微分方程的求解方法包括有限元、有限差分、变分法和边界元法等，对于多相、多组分的微分方程，可采用较为完善和成熟的有限差分求解［13-14］，三维情况可采用七点差分格式［15］，基质系统的差分方程为

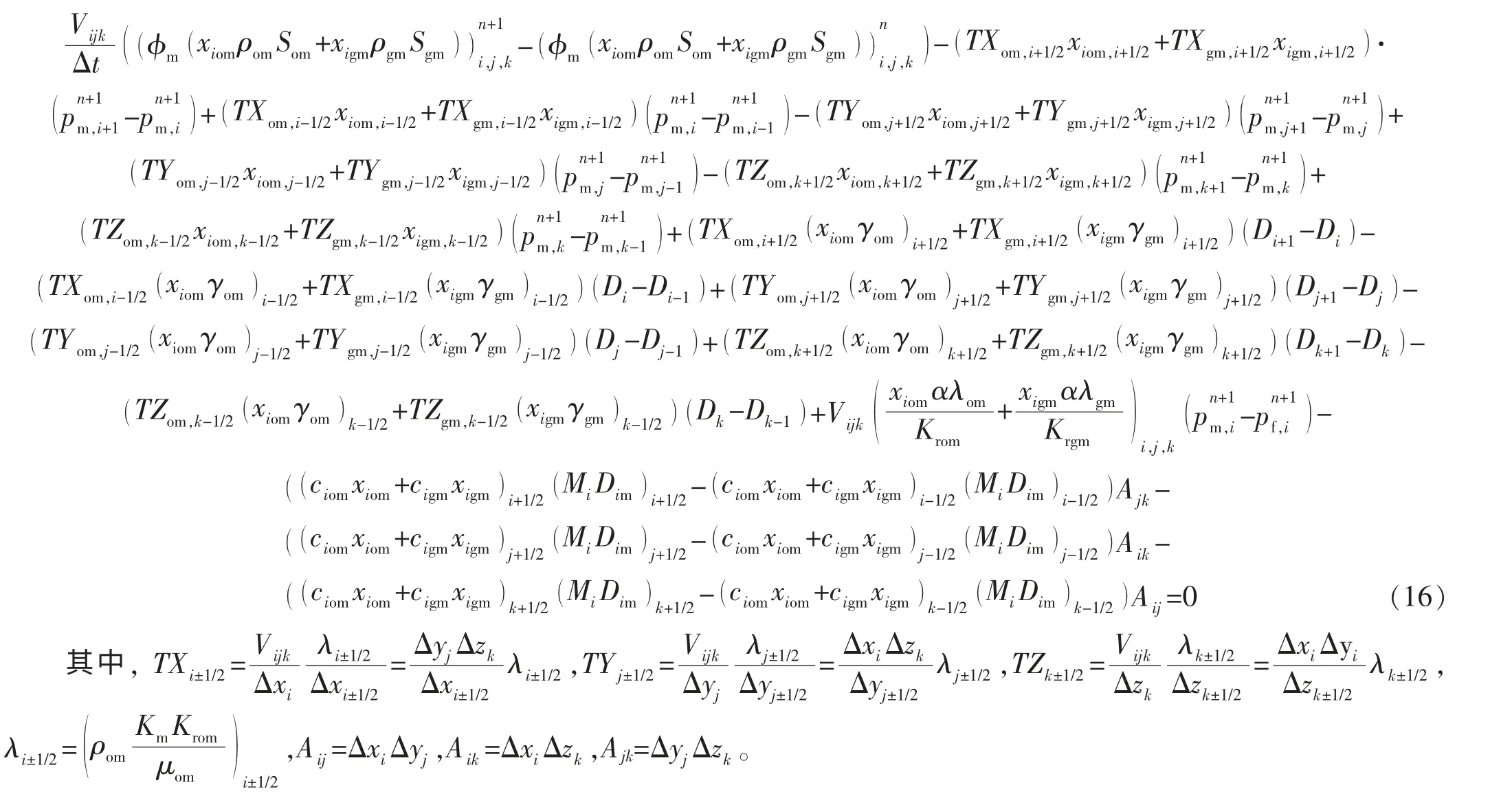
裂缝系统的差分方程为

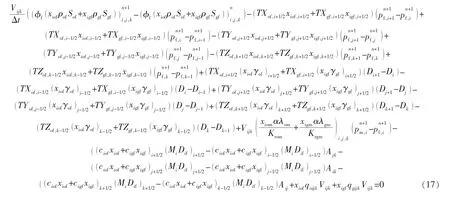
对多相、多组分微分方程的求解，必须考虑相态平衡。相态拟合采用SRK3 状态方程，黏度系数类型选择采用Lorenz-Bray-Clark，相对渗透率的确定和计算采用Stone 经验公式，按顺序求解方法建立隐式压力显式饱和度数值求解模型。具体步骤为［16-17］：1）建立压力、饱和度和总组成差分方程组，用牛顿迭代法将非线性压力差分方程组线性化，并形成主对角占优的雅可比矩阵；2）将上一时间步（n 时间步）的压力、饱和度、总组成、 液相和气相浓度等迭代初值，采用单点上游权、 双点上游权分别计算本时段初始时刻网格界面上各相的摩尔流动系数，并确定网格界面上油、气两相流的组成；3）在第n+1 时间步，构建第l 次压力值的雅可比系数矩阵，并求解第l+1 次压力迭代值；4）根据第l+1 次压力迭代值，计算第l+1 次含水饱和度和总组成迭代值；5） 根据第l+1 次压力迭代值和总组成迭代值进行相平衡计算；6） 评判第l 次和第l+1 次这两次压力迭代值，若达到精度要求，则进入下个时间段（n+2时间步）的计算，即第2）步，否则重复步骤3），4），5）直到满足精度要求为止。

4 实例分析

某裂缝性碳酸盐岩油藏［18］，总体表现出低孔、低渗特征，储层基质孔隙度为2.64%～7.20%，基质渗透率为0.05×10-3～0.80×10-3μm2，裂缝渗透率为100 μm2。地层流体表现出低密度、低黏度、低含硫、低含胶质的特点，原油相对密度0.84 t/m3，20 ℃时原油黏度6.8 mPa·s，蜡体积分数6.8%，硫体积分数0.8%，油藏温度43.3 ℃。油气界面GOC 为309.4 m，对应的地层压力为9.73 MPa；油水界面WOC 为940.9 m，对应的地层压力为14.40 MPa。

细管实验法是确定最小混相压力（MMP）常用的有效方法，可以模拟CO2注气过程的多级接触混相过程。通过分析注入1.2 PV CO2时的采收率来确定MMP，但这种传统的细管方法仅仅依靠采收率判断，具有局限性。研究表明，在近混相中的采收率仍然可以达到90%以上，另外，裂缝的存在对流体混相效果也有影响［19］。本文在考虑裂缝影响条件下，根据注入1.2 PV CO2时的采收率和观察流体颜色变化判断混相时机，能够准确预测MMP。在实验温度43.3 ℃条件下，进行了5 组不同驱替压力的细管实验，分别为6.9，10.3，13.8，17.2，20.7 MPa。实验表明：当驱替压力小于MMP时，产出的流体颜色与原样品颜色大致相同，并无变化；当驱替压力大于MMP 时，产出的流体颜色明显变浅。图1给出了不同驱替压力条件下，注入1.2 PV CO2时的最终采收率，由此可以确定MMP 为10.3 MPa。由于油藏压力大于MMP，所以在地层条件下，CO2能够混相。

图1 不同驱替压力下原油的最终采收率

为了验证前面建立的考虑分子扩散的多相、 多组分双重介质模型（Model 1）的可行性，并且评价分子扩散的影响效果，应用Eclipse 软件建立了基质/裂缝双重介质组分模型（Model 2）。模型中的裂缝系统采用局部网格加密等效处理，采用正方形油藏模型进行模拟。如图2所示，模型基质被裂缝系统分割成75 块，每个基质块由25 个网格组成，每个网格平面步长为20 m，垂向步长为1.33 m，因此模拟油藏面积为0.25 km2，有效厚度为4 m。在油藏对角线上分布一注一采2 口直井，生产井所在的平面网格坐标为（3，3），注气井所在的平面网格坐标为（27，27）。

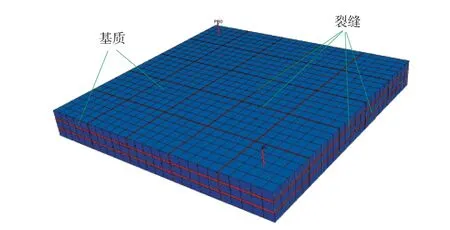
图2 基质/裂缝双重介质模型

在裂缝性碳酸盐岩油藏注气过程中，气体在驱动力的作用下进入裂隙，气体分子与基质或死孔隙中的原油发生分子扩散作用，进行质量传递，同时降低油气界面张力，从而有效驱替基质孔隙中的残余油。图3给出了注入不同体积CO2后的油藏饱和度分布，可以看出气驱前缘并不均匀。图3b和图3c显示气体优先占据裂缝系统，然后与周围基质进行渗流和扩散传质作用，导致裂缝系统周围的含油饱和度明显较低，扩大了与外围基质的油气分子浓度差，由此扩散作用继续向外围扩展，最终将整个油藏驱替得较为彻底。

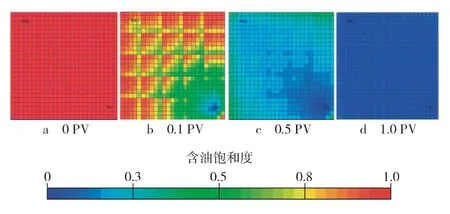
图3 不同注入体积气驱油藏后含油饱和度分布

图4为基质岩块在注入不同体积CO2后的界面张力剖面。可以看出，界面张力在混相前缘急剧降低，达到了混相效果，随着混相面积的扩大，界面张力下降的面积增大，在混相波及范围内，CO2不仅溶解于原油中，而且对原油中较轻、或者中间的烃类组分有抽提作用，这减小了原油与气体的黏度、密度等差异，从而提高了气体驱替效率。

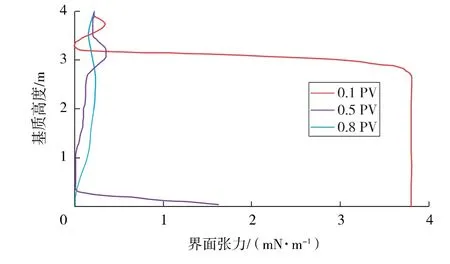
图4 不同注入体积的气驱界面张力剖面

图5和表1给出了模拟结果。通过图5可以看出：1）三者在早期的采出程度变化一致，论证了模型的可靠性；2）不考虑分子扩散作用的Model 1（假定扩散系数为0）和Model 2 采出程度曲线拟合精度高，进一步论证了模型的可信性；3）随着开发的进行，考虑分子扩散作用的Model 1 采出程度进一步提高，当注入1.0 PV 的CO2时，采出程度提高了6.47%，提高幅度达10.82%，这是因为扩散作用扩大了CO2混相驱波及面积。分子扩散对CO2混相驱的影响见表1。由表1可知：早期，扩散作用对混相面积和采出程度影响较小，随着注气开发的进行，对混相面积的影响越来越明显，但是随着开发的进一步进行，混相面积有变小的趋势，这与原油组分和油藏压力的变化等因素有关。

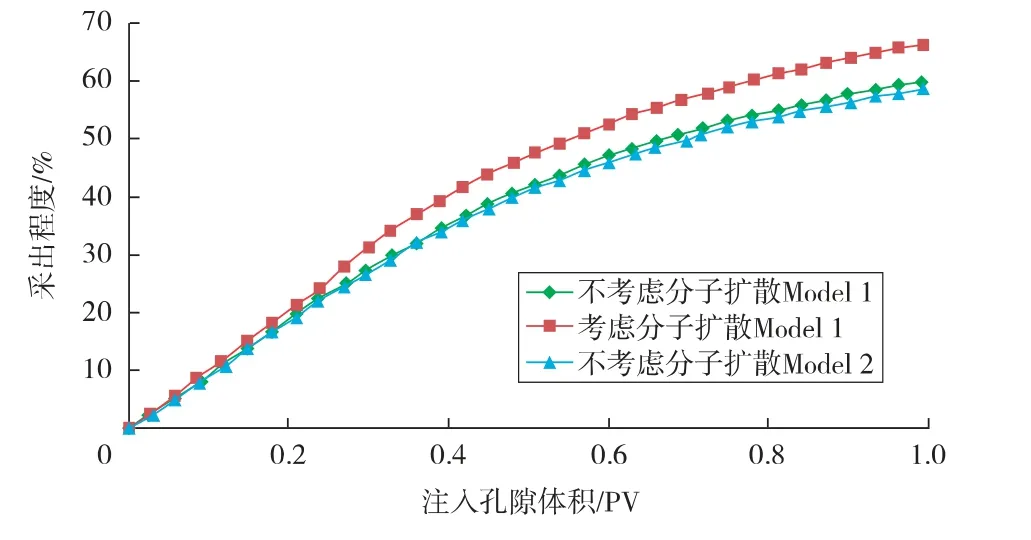
图5 分子扩散对CO2 混相驱采出程度影响

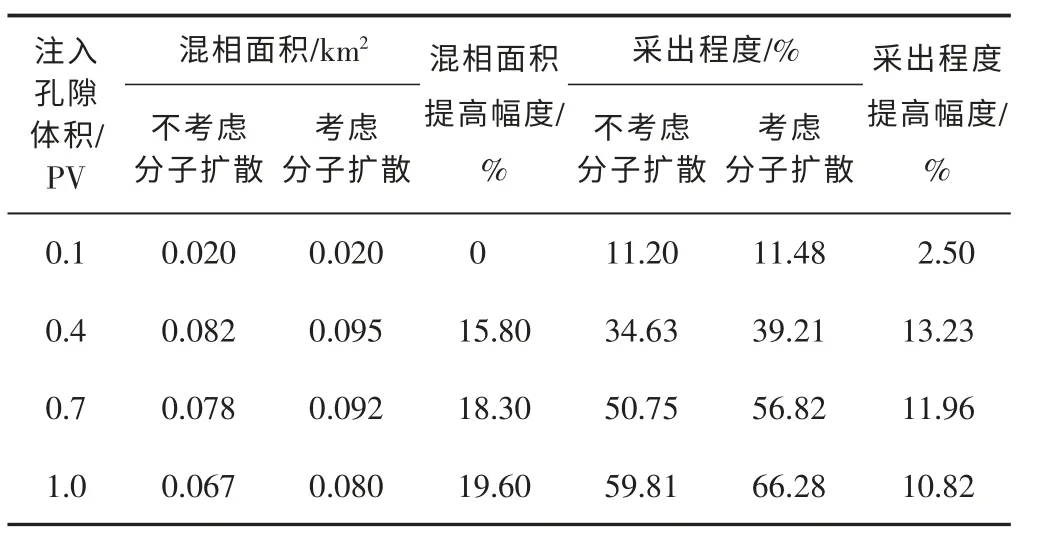
表1 混相面积和采出程度对比

5 结论

1）综合考虑分子扩散作用的影响和多组分相态变化规律，建立了考虑分子扩散作用的多相、多组分数学模型，弥补了现有模型描述裂缝性油藏CO2混相驱渗流规律方面的不足。

2）通过实例分析对比，考虑或不考虑分子扩散的多相、多组分模型和Eclipse 常规模型，三者在初期采出程度变化规律相同，分子扩散在初期对产能影响较小，但中后期影响表现明显，分子扩散作用使得CO2混相驱降低界面张力的效果更明显，而且能增大混相面积和提高驱替效率。同时，与Eclipse 常规模型计算结果的对比，论证了该模型的可靠性，对裂缝性油藏注气动态预测有一定指导意义。

［1］李士伦，郭平，戴磊，等.发展注气提高采收率技术［J］.西南石油学院学报，2000，22（3）：41-45.

［2］文玉莲.裂缝性油藏注气开发分子扩散行为研究及数值模拟［D］.成都：西南石油大学，2005.

［3］苏玉亮，吴晓东，侯艳红，等.低渗透油藏CO2混相驱油机制及影响因素［J］.中国石油大学学报：自然科学版，2011，28（3）：99-102.

［4］孙晓旭，杨胜来，吴晓云.裂缝性底水潜山油藏注气数值模拟研究［J］.复杂油气藏，2012，23（1）：63-66.

［5］宋道万.二氧化碳混相驱数值模拟结果的主要影响因素［J］.油气地质与采收率，2008，15（4）：72-74，115-116.

［6］李南，程林松.低渗透油藏CO2混相驱过程中考虑对流扩散的流固耦合模型研究［J］.岩石力学与工程学报，2012，31（增1）：3055-3060.

［7］Kastw，Hohenthanner C R.Mass transfer within the gas-phase of porous media［J］.International Journal of Heat and Mass Transfer，2000，43（5）：807-823.

［8］姚军，孙海，樊冬艳，等.页岩气藏运移机制及数值模拟［J］.中国石油大学学报：自然科学版，2013，30（1）：91-98.

［9］王利生.驱替气体在油藏流体中的对流扩散（I）［J］.石油勘探与开发，1996，23（6）：62-66，97.

［10］梅海燕，张茂林，李闽.气驱过程中考虑弥散的渗流方程［J］.天然气工业，2004，24（3）：98-99，150.

［11］Hussein Hoteit，Abbas Firoozabadi.Numerical modeling of diffusion in fractured media for gas-injection and recycling schemes［R］.SPE 103292，2009.

［12］Kazemi H，Merrill L S，Porterfield K L，et al.Numerical simulation of water-oil flow in naturally fractured reservoirs［R］.SPE 5719，1976.

［13］Peng C P，Yanosik J L，Stephenson R E.A generalized compositional model for naturally fractured reservoirs［R］.SPE 16340，1989.

［14］Young L C，Stephenson R E.A generalized compositional approach for reservoir simulation ［R］.SPE 10516，1983.

［15］张烈辉.油气藏数值模拟基本原理［M］.北京：石油工业出版社，2005：120-190.

［16］张茂林，孙良田，李士伦，等.凝析油气藏K 值多组分模型数值模拟方法［J］.石油学报，1991，12（1）：60-66.

［17］张茂林，孙良田，李士伦，等.分数步长算法在K 值多组分模型中的应用［J］.天然气工业，1991，11（4）：51-56.

［18］Alavian S A，Whitson C H.CO2IOR potential in naturally fractured Haft Kel Field，Iran［R］.IPTC 10641，2005.

［19］Knut Uleberg，Lars Hoier.Miscible gas injection in fractured reservoirs［R］.SPE 75136，2002.