新型裂缝性页岩气藏物质平衡方程

王怀龙，张茂林，郭沙沙，梅海燕

（西南石油大学油气藏地质及开发工程国家重点实验室，四川 成都610500）

0 引言

页岩气是一种赋存于泥岩、 页岩中的非常规天然气，它的形成和富集具有自生自储的特点［1-3］。页岩气通常以自由态和吸附态存在于储层之中［4］。吸附气存在于富含有机质、黏土的页岩基质中，自由气存在于富含石英的基质孔隙和裂缝之中［5］，并且高产的页岩气藏通常发育大量的天然裂缝［6-7］。

页岩气藏的储量评价是十分重要的［8-9］。物质平衡方程是确定原始气体储量和预测常规气藏生产动态的基本工具［10-11］。之前很多学者推导的物质平衡方程往往忽略了吸附相所占据的孔隙体积，这无疑高估了自由气的地质储量。本文从质量守恒方面考虑了页岩气吸附相体积的变化，又从体积守恒方面分别考虑基质和裂缝双重孔隙系统［12］，推导了新的物质平衡方程。

1 页岩气吸附特征

1.1 吸附等温线的选择

在对页岩气吸附的拟合过程中，L-F 模型与Langmuir 模型的拟合程度均大于99%，而Freundlich模型的拟合度较低，同时，Langmuir 模型相对于Frenudlich 模 型 与L-F 模 型 在 形 式 上 更 便 于 计 算［13］；因此，本文采用Langmuir 模型来描述页岩的等温吸附过程。假设页岩气藏开发处于等温状态，页岩气吸附等温式为［14］

式中：p 为当前地层压力，MPa；VE为地层压力p 下的等温吸附量，m3/m3；VL为兰氏体积，m3/m3；pL为兰氏压力，MPa。

1.2 页岩气吸附相密度

由于储层温度明显高于天然气的临界温度，这就很难确定吸附相是以液态还是气态形式存在［15］。页岩中微孔隙的孔隙壁对甲烷的吸附力很强，使得吸附态的密度可以变得很高。在许多情况下，吸附相的密度甚至比其液相密度还要高。在储量计算时，考虑到微孔隙的吸附能力，以及在页岩和煤层当中的微孔隙数量，吸附相的密度是必须要求取的重要参数。目前获得吸附相密度的方法主要有实验法和分子模拟法。

1.2.1 实验法

Dubinin［16］通过范德华方程以及2 个经验公式，得到了吸附态甲烷的密度为0.371 0 g/cm3。

Haydel 和Kobayashi［17］在较低的压力（6.895 MPa）和温度（40 ℃）下使用无机壁SiO2进行实验，得到吸附相密度为0.374 0 g/cm3。

Menon［18］提出吸附相的密度等于该物质液相的密度。Tsai［19］等将液相密度具体化，认为吸附相密度等于该物质临界点处的密度。对于这种观点，Mavor［20］通过实验发现，吸附相密度应采用0.101 MPa，-161 ℃条件下液态甲烷的密度0.422 3 g/cm3。

1.2.2 分子模拟法

快速发展的分子模拟技术解决了实验过程中的诸多困难，为研究小孔隙的吸附提供了可能［21-22］；但由于模型、算法、模拟软件的不一致，得到的吸附相密度差异很大。

Ambrose 结合分子模拟和Langmuir 方程，得出吸附相密度为0.340 0 g/cm3［23］。通过分子模拟，Ambrose也证明了Langmuir 单层分子吸附理论可以很好地描述甲烷分子在固体表面的吸附规律。

2 物质平衡方程的建立

根据体积守恒原理建立物质平衡方程：

式中：Gp为采出气体的体积，m3；Vm，Vf分别为基质、裂缝中剩余自由气在地面条件下的体积，m3；Va为剩余吸附气在地面条件下的体积，m3；Gm，Gf分别为原始地层条件下基质、 裂缝中自由气在地面条件下的体积，m3；Vai为原始地层条件下吸附气在地面条件下的体积，m3。

根据Langmuir 吸附定律可知，在原始地层压力pi下的吸附气在地面条件下的体积Vai为

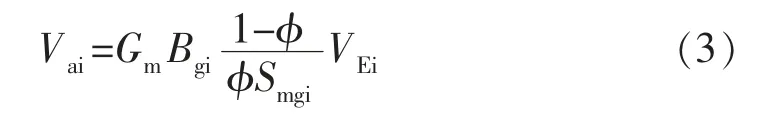
式中：Bgi为原始地层压力下的天然气体积系数；φ 为基质系统孔隙度；Smgi为原始地层条件下基质中的自由气饱和度；VEi为原始地层压力下的等温吸附量，m3/m3。

当前地层压力p 下的吸附气在地面条件下的体积Va为

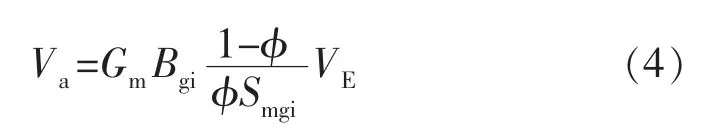
在地层压力p 下，裂缝中剩余自由气在地面条件下的体积为

式中：Bg为当前地层条件下的天然气体积系数；Sfgi为原始地层条件下裂缝中的自由气饱和度；Cf为裂缝压缩系数，MPa-1；Cw为束缚水压缩系数，MPa-1；Sfwi为裂缝中束缚水饱和度；Δp 为原始地层压力与当前地层压力的差值，MPa。

开采后基质中剩余气体在地面条件下的体积为

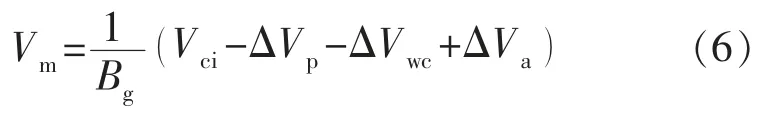
式中：Vci为原始地层条件下基质中的孔隙体积，m3；ΔVp为基质岩石孔隙体积的收缩量，m3；ΔVwc为基质中束缚水体积的膨胀量，m3；ΔVa为吸附气体积在地层条件下的减少量，m3。

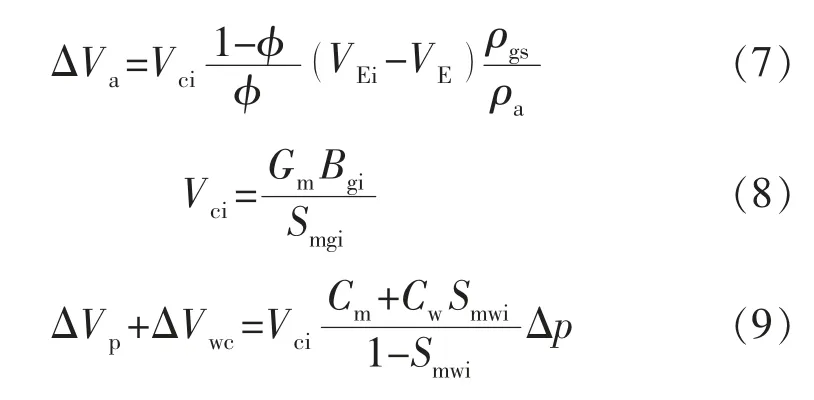
式中：ρa为吸附气在地层条件下的密度，g/cm3；ρgs为天然气在标准状况下的密度，g/cm3；Smwi为基质中束缚水饱和度；Cm为基质压缩系数，MPa-1。

将式（7）—（9）代入式（6）中得到：

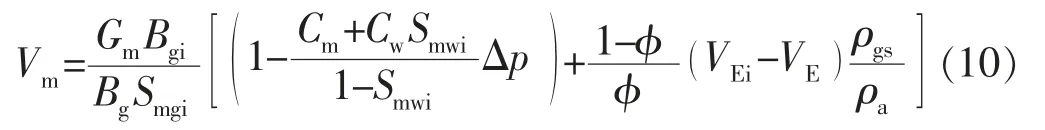
将式（3）—（5）和式（10）代入式（2）中得到：

式（11）即可简化为

通过式（12）可以建立Y 和X 之间的线性关系，根据直线方程的斜率和截距可以分别得出基质中自由气的储量Gm和裂缝中自由气的储量Gf，通过Gm和式（3）可以得到吸附气的储量Vai，最后将3 种储量相加便可以得出单井控制储量。

3 实例计算

某页岩气藏的基本参数如下：pi＝24.138 MPa，Bgi=4.46×10-3，Cm=4.35×10-4MPa-1，Cf=8.7×10-3MPa-1，Cw=4.35×10-4MPa-1，Smwi=20%，Sfwi=5%，ρgs＝0.66×10-3g/cm3，φ＝4.3%，VL＝13.53 m3/m3，pL＝19.895 MPa，生产数据如表1所示。

当吸附相密度选取中间值0.422 3 g/cm3时，利用式（12）回归Y 和X 之间的关系（见图1）。从图1可以得到，基质中的自由气储量为5 519.98×104m3，裂缝中的自由气储量为4 167.80×104m3。同时，利用式（3）可以得到吸附气储量为7 478.40×104m3。从而可以得到此单井控制储量为17 166.18×104m3。其中，裂缝中储量占总储量的24.28%，吸附气储量占总储量的43.56%。

表1 某页岩气藏生产数据

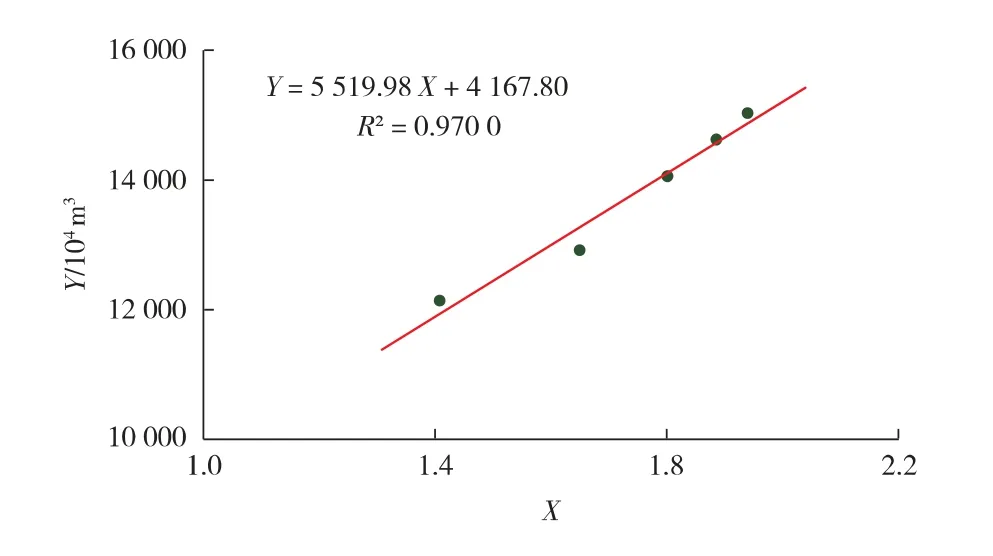
图1 新型物质平衡方程的储量回归

利用常规物质平衡方程［24］得到的天然气储量为15 815.50×104m3。常规方法忽略了吸附气的存在，这就极大地低估了页岩气井的单井控制储量。本文推导的物质平衡方程，充分考虑了吸附相特征，可以分别得到吸附气、自由气储量，显然本文方法和实际情况更为接近。利用本文方法可以得到不同吸附相密度条件下的储量（见表2）。

图2为吸附相密度对储量的影响。可以看出：随着吸附相密度的增加，基质中的自由气、吸附气以及总储量都是逐渐增加的，裂缝中的自由气逐渐减少。

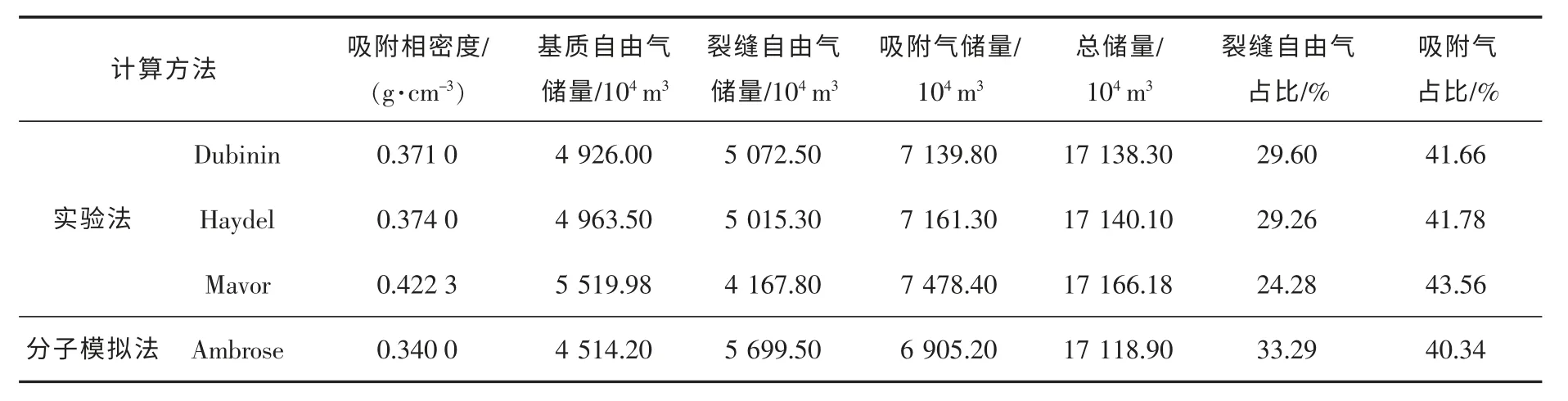
表2 不同吸附相密度值所对应的储量及吸附气占比

图2 吸附相密度对储量的影响

4 结论

1）本文推导的物质平衡方程，同时考虑了孔隙和裂缝2 个系统以及吸附相体积随压力变化的情况，克服了常规体积守恒方法不能分别计算吸附气、 自由气储量的缺点，可以更为精确地计算气藏的可控制储量。

2）通过实例计算发现，发育裂缝的页岩气藏裂缝中自由气储量占总储量的24.28%～33.29%，在低孔隙度的基质中，储量主要由吸附相提供；随着吸附相密度的增加，基质中的自由气、吸附气储量以及总储量逐渐增加，裂缝中的自由气储量逐渐减少。

3）本文方法充分考虑了在页岩气藏开采过程中，由吸附层体积变化而引起的自由气空间增大情况，希望能为今后的研究提供帮助。

［1］郭少斌，黄磊.页岩气储层含气性影响因素及储层评价：以上扬子古生界页岩气储层为例［J］.石油实验地质，2013，35（6）：601-606.

［2］张田，张建培，张绍亮，等.页岩气勘探现状与成藏机理［J］.海洋地质前沿，2013，29（5）：28-35.

［3］朱彤，曹艳，张快.美国典型页岩气藏类型及勘探开发启示［J］.石油实验地质，2014，36（6）：718-724.

［4］邵晓州，余川，付勋勋，等.页岩气研究新进展及开发瓶颈分析［J］.断块油气田，2012，19（6）：764-766.

［5］任珠琳，李晓光，王龙，等.辽河东部地区梨树沟组页岩气富集条件及有利区优选［J］.断块油气田，2013，20（6）：704-708.

［6］李新景，胡素云，程克明.北美裂缝性页岩气勘探开发的启示［J］.石油勘探与开发，2007，34（4）：392-400.

［7］王南，钟太贤，刘兴元，等.复杂条件下页岩气藏生产特征及规律［J］.断块油气田，2012，19（6）：767-770.

［8］曲占庆，林珊珊，张杰，等.多组分和吸附对页岩气储量计算的影响［J］.特种油气藏，2012，19（3）：114-116，143.

［9］Firanda E.The development of material balance equations for coalbed methane reservoirs［R］.SPE 145382，2011.

［10］King G R，华桦.关于有限水侵的煤层和泥盆系页岩气藏的物质平衡方法［J］.天然气勘探与开发，1994，17（1）：63-70.

［11］Ciancaglini M，Cabrapan Duarte J C，Caliz E A.Material balance analysis of naturally or artificially fractured shale gas reservoirs to maximize final recovery［R］.SPE 169480，2014.

［12］张广东，刘建仪，李祖友，等.裂缝气藏物质平衡方程［J］.天然气工业，2006，26（6）：95-96.

［13］郭为，熊伟，高树生，等.页岩气等温吸附/解吸特征［J］.中南大学学报：自然科学版，2013，44（7）：2836-2840.

［14］傅献彩，沈文霞，姚天扬，等.物理化学［M］.北京：高等教育出版社，2006：360-375.

［15］Hartman R C，Ambrose R J，Akkutlu I Y，et al.Shale gas-in-place calculations（Part Ⅱ）：Multicomponent gas adsorption effects［R］.SPE 144097，2011.

［16］Dubinin M M.The potential theory of adsorption of gases and vapors for adsorbents with energetically nonuniform surfaces［J］.Chemical Review，1960，60（2）：235-241.

［17］Haydel J J，Kobayshi Riki.Adsorption equilibria in the methanepropane-silica gel system at high pressures［J］.Industrial Engineering Chemical Fundament，1967，6（4）：564-554.

［18］Menon P G.Adsorption at high pressures［J］.Chemical Reviews，1968，68（3）：277-294.

［19］Tsai M C，Chen W N，Cen P L，et al.Adsorption of gas mixture on activated carbon［J］.Carbon，1985，23（2）：167-173.

［20］Mavor M J，Hartman C，Pratt T J.Uncertainty in sorption isotherm measurements ［C ］.Tuscaloosa ：International Coalbed Methane Symposium，2004.

［21］Liu Y，Wilcox J.Molecular simulation of CO2adsorption in micro-and mesoporous carbons with surface heterogeneity ［J］.International Journal of Coal Geology，2012，104：83-95.

［22］Liu Y，Wilcox J.Effects of surface heterogeneity on the adsorption of CO2in microporous Carbons［J］.Environmental Science＆Technology，2012，46（3）：1940-1947.

［23］Ambrose R J，Hartman R C，Diaz-Campos M，et al.Shale gas-in-place calculations（Part Ⅰ）： New pore-scale considerations［R］.SPE 131772，2010.

［24］张广东，刘建仪，李祖友，等.裂缝气藏物质平衡方程［J］.天然气工业，2006，26（6）：95-96.