基于数据场与云模型的多模雷达信号分选算法
国 强,宋文明,南普龙,万 建
(哈尔滨工程大学信息与通信工程学院,150001哈尔滨)
基于数据场与云模型的多模雷达信号分选算法
国 强,宋文明,南普龙,万 建
(哈尔滨工程大学信息与通信工程学院,150001哈尔滨)
针对传统分选算法处理多模雷达信号效果较差的问题,提出一种基于数据场的层次聚类信号分选算法,以克服多模雷达信号分选时存在的“增批”问题.将数据场理论应用于多模雷达辐射源信号的分选,利用数据场势函数划分辐射源信号数据的层次,通过等势图的绘制完成数据的自组织层次聚类.提出一种基于云模型的分选结果有效性评估算法,可在脱离雷达辐射源库的情况下验证信号分选结果的有效性.仿真实验验证了提出算法的有效性.
多模雷达;数据场;云模型;信号分选
多模雷达是指集多种体制雷达功能于一身,具备多种工作模式,可以同时完成多种作战任务的新型雷达[1].为提高工作性能并满足抗干扰的需求,多模雷达多采用复杂多变的波形设计,雷达发射脉冲的频率、时域参数都进行复杂的变化,其雷达信号特征参数空间复杂多变、不具备明显的相关性和规律性.随着电子对抗设备的日益先进和脉冲密度的迅猛增加,电子侦察设备接收到的雷达信号及雷达辐射源数据库常呈现出明显的随机性和模糊性.因此在对多模雷达信号分选时,往往会将一个辐射源的不同模式分选为多个辐射源,造成“增批”现象[2].
从数据挖掘的角度来看,领域内提出的多模雷达信号分选算法分为分类算法和聚类算法.典型的分类方法主要包括基于神经网络[3]和基于支持向量机[4]的分选方法.此类方法在处理未知信息过多、样本集过于复杂、样本随机性与模糊性较高的雷达信号时,会产生大量不可预测结果.聚类算法相比于分类算法在处理高密度、具有随机性和模糊性、数据成分复杂的雷达信号更有优势.具有代表性的聚类分选算法法有K-means算法[5]以及网格密度聚类算法[6].当前应用于雷达信号分选的聚类算法存在以下问题:抗噪能力和发现任意形状、大小聚类的能力较弱,处理离散数据效果较差.
本文受数据挖掘理论[7]启发,提出一种基于数据场与云模型的多模雷达信号分选算法.为验证算法分选结果的有效性,提出一种基于云模型理论的多模雷达信号分选结果评估算法,将每个预分选算法得到的聚类结果归纳为一个云模型,根据提出的评价判定准则比较、处理不同云模型间的隶属度,从而验证分选结果的有效性并进一步提高分选正确率.
1 基于数据场的层次聚类分选算法
由于层次聚类具有通过层次构架模式递归地对数据进行合并或分裂,形成一种嵌套的类层次结构或类谱系图的特点,可将一部多模雷达的不同模式雷达信号归纳为同一谱系,适用于多模雷达信号的分选.考虑到当前复杂密集电磁环境中截获到的雷达信号存在大量噪声与离群数据,且由于雷达信号先验信息的缺失,层次聚类的参数无法进行设定.因此本文引入数据场理论,利用数据场构建辐射源信号的等势线划分,采用削除势心法确定信号样本的势心作为层次聚类的聚类中心,通过势场的建立完成数据的自组织层次聚类.
1.1 数据场理论
数据场理论借用物理中场的概念,将数据空间中每个数据点视为多维数据空间中具有一定质量的粒子,每个粒子周围存在一个虚拟作用场,数据空间中其他数据点将受到该点场力的作用,同时该粒子也会受到其他粒子场力的作用.设已知空间Ω中包含n个对象的数据集D={x1,x2,…,xn},数据空间中任一点的势是数据空间其他点到该点的势值加和[8],即
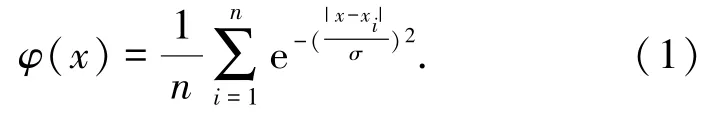
式中:‖x-xi‖为数据点数据对象x到空间任意点xi的欧式空间距离;σ是影响因子,用于控制对象间的相互作用力.
这里需要指出,由于雷达样本信号不同特征参数的数值差异很大,在利用式(1)求取数据空间某一点的数值前,须对雷达信号各参数进行归一化处理:雷达某一特征参数向量A=[a1,a2,…,an]归一化后得到A′=[a1′,a2′,…,an′],其中ai′=-1+2×(ai-amin)/(amax-amin).数据的归一化处理可以简化数据场的构建,更有效地表现数据的密集程度.为了更好地对势场进行量化分析,将势值相同的点连接起来构成等势线.等势线是数据空间中所有数据形成的数据场叠加而形成的嵌套模型,可以定量描述数据空间中数据点的分布.图1是数据场等势线分布示意图,可见等势线密度与数据点的密集程度成正比.图1中等势线围绕的位置为势心,是势场中势值的极大值点.势心由代表数据点的某个或多个特征参数的空间分布情况决定,可以最大程度代表该势心附近所有点的空间特征.当将数据场应用于聚类算法中时,可将势心作为数据空间中特征参数聚类分选算法的聚类中心.
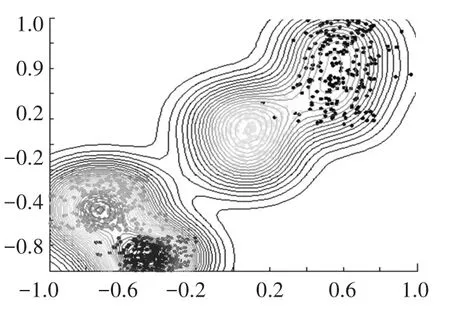
图1 数据场等势线分布图
1.2 改进的影响因子选取方法
根据式(1)可知,数据对象的作用距离与σ值的大小成正比.图2给出当σ取不同值时势场的分布情况.若σ值足够大,整个数据场可以理解为只有一个势心的数据集合,如图2(c)所示.此时的数据场显然不能准确反映数据点的分布情况,因此一个合适的影响因子值对数据场的构建至关重要.本文提出一种改进的影响因子选择方法,以克服数据挖掘算法需要用户仔细选择参数的问题.
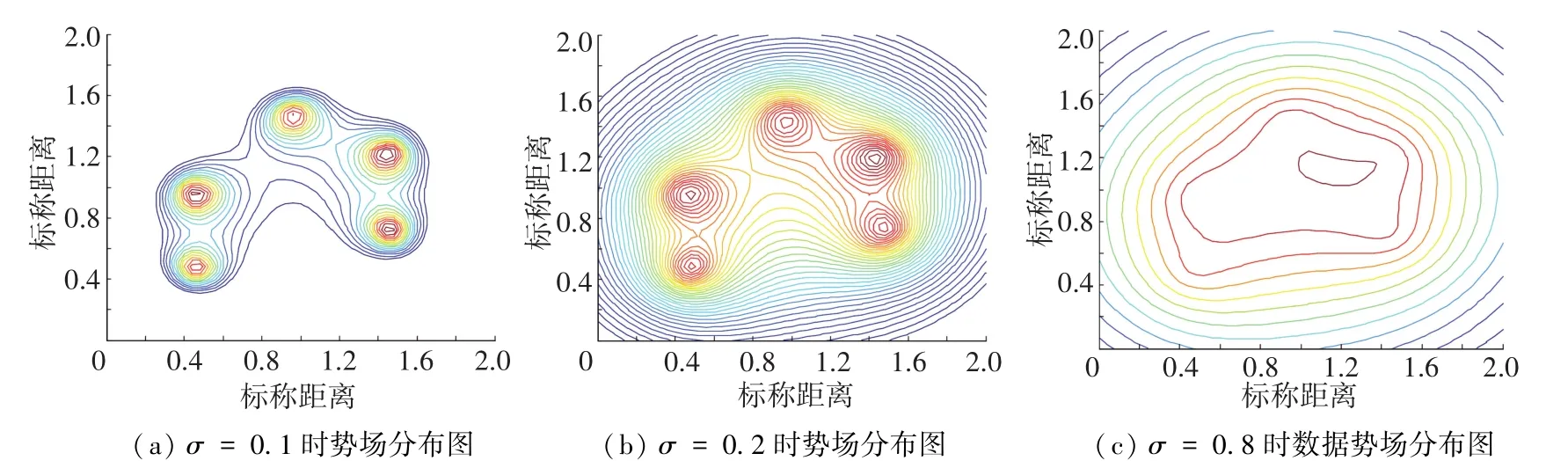
图2 影响因子σ对数据势场分布的影响
基于信息论中表征系统不确定性的熵的概念,引入势熵来衡量不同影响因子对构成势场的影响.
令数据点x1,x2,…,xn的势值分别为Ψ1,Ψ2,…,Ψn,则势熵可以定义为
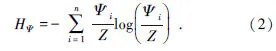
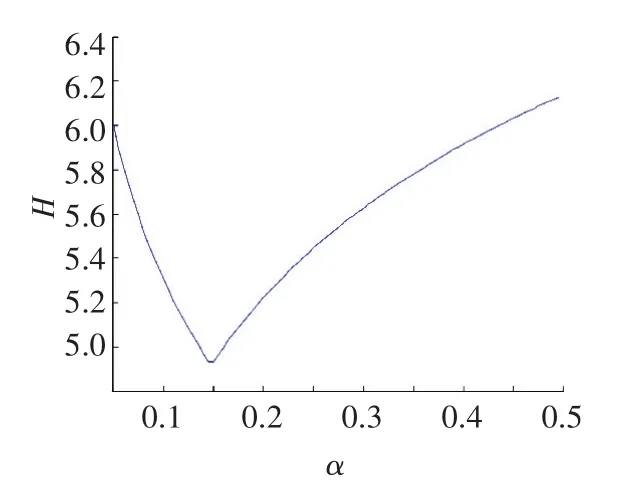
图3 势熵H与σ间的关系曲线
根据上述分析,σ的选择可以转化为寻找势熵最小值的过程.该改进算法可以在不需要人工选择的情况下自动选择最佳的影响因子.
1.3 基于数据场的层次聚类算法实现步骤
已知样本空间Ω⊆R3中n个输入多模雷达信号样本集D={x1,x2,…,xn},每个样本由特征参数DOA、PW、RF构成.基于数据场的层次聚类多模雷达信号分选的具体步骤为:
1)从信号样本集D中随机抽取nsample≪n雷达信号,对信号各参数进行归一化处理,采用影响因子优化选取算法确定影响因子σ.
3)对划分后的网格空间进行数据场势值计算,并绘制等势线.
4)采用削除势心法找到数据空间中的势心值.
5)将数据空间中的所有势心值作为层次聚类的聚类中心,按照等势线所形成的嵌套结构进行层次划分,完成多模雷达信号的分选.
1.4 仿真实验分析
为验证基于数据场的层次聚类算法处理多模雷达信号的有效性,利用表1中的多模雷达信号脉冲仿真数据对该分选算法进行仿真实验.
表1中雷达1与雷达4分别为具有3种工作模式的先进体制多模雷达信号,图4为表1中雷达信号的和二维仿真图.如图4所示,雷达1与雷达4的信号不同工作模式间参数差异性明显,采用传统模糊聚类分选算法[9]进行分选,结果如图5所示,此时会出现将雷达信号的某一工作模式分选为其他辐射源的情况,出现“增批”现象.

表1 雷达脉冲参数仿真数据
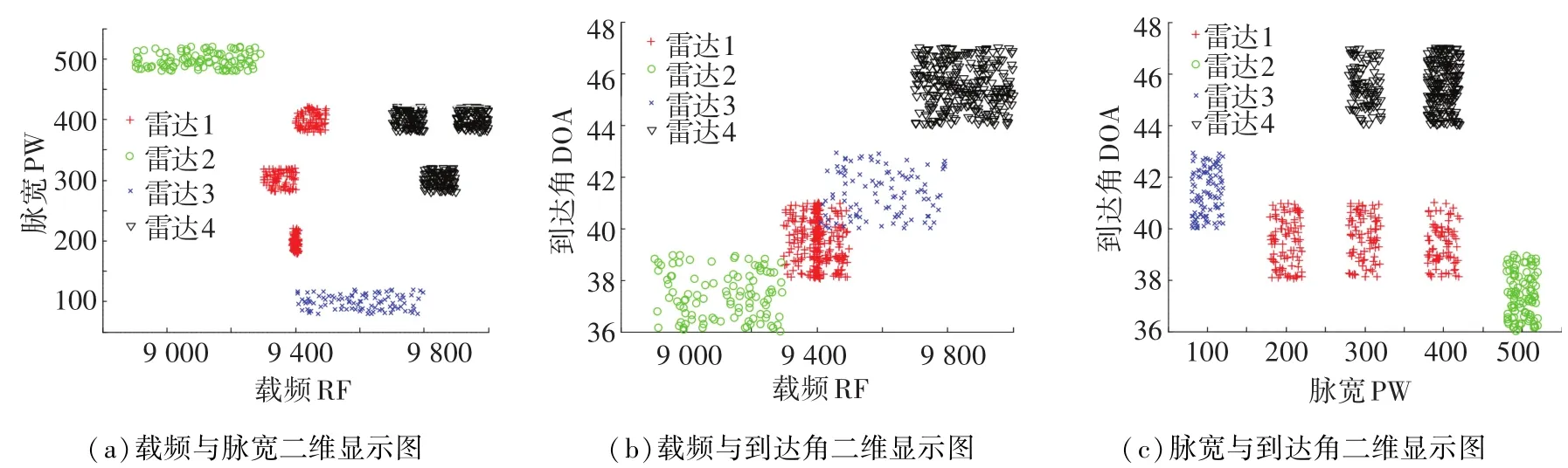
图4 雷达信号脉冲数据二维显示图

图5 模糊聚类处理信号样本的分选结果
采用基于数据场的层次聚类算法对雷达信号样本进行处理,归一化各组特征参数数值,确定最优影响因子值,计算信号样本的势值,进而生成数据场绘制等势线,结果如图6所示.
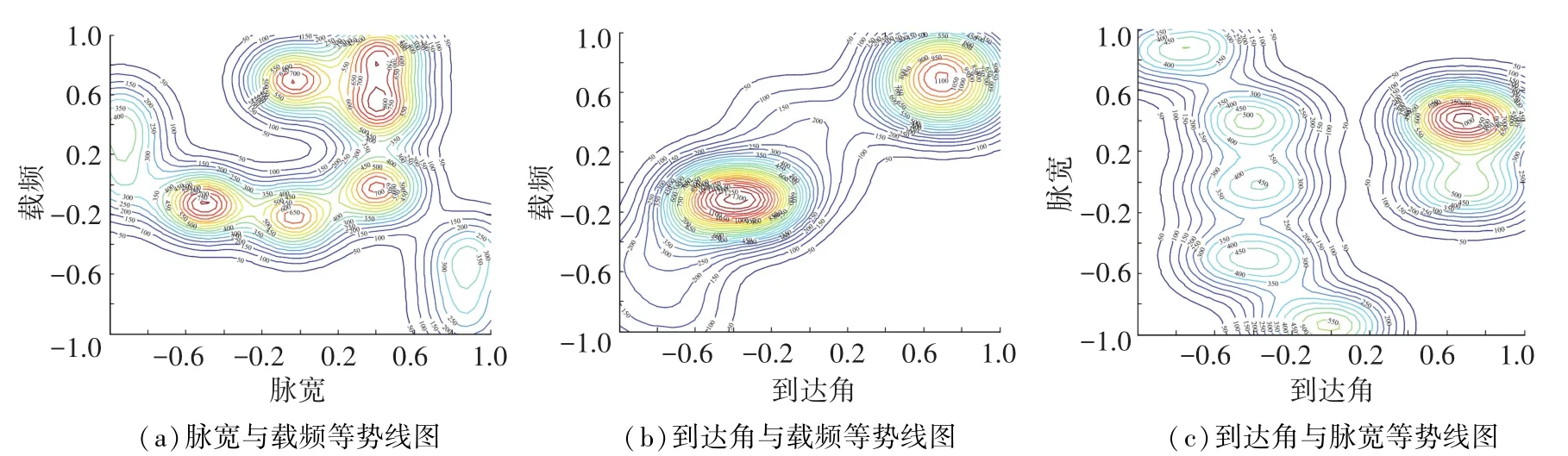
图6 数据场算法处理信号样本生成的数据场等势线二维图
利用图6中生成的等势线分布和削除势心法得到的聚类中心值与聚类数目,对信号样本进行层次聚类分选,结果如表2所示.
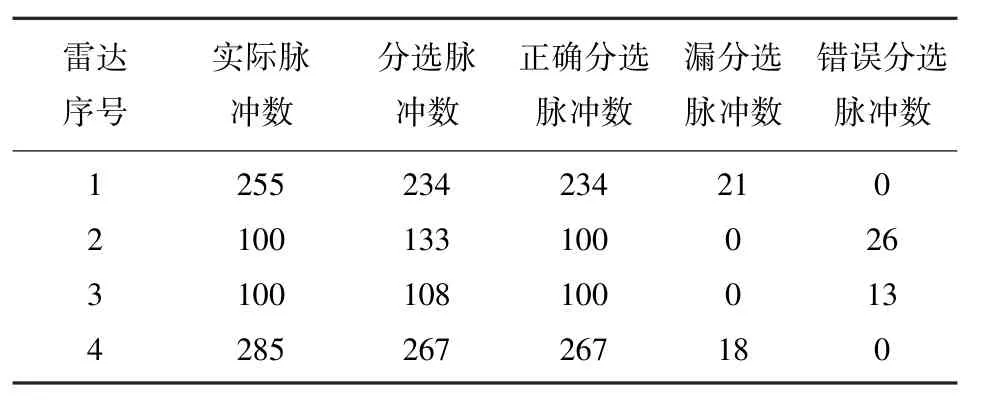
表2 基于数据场的层次聚类算法分选结果
将基于数据场的层次聚类算法分选结果与表3中传统模糊聚类分选结果比较,可以发现本文所提出方法可以较好处理多模雷达信号,分选性能优于传统聚类算法.但从表2中可以发现,雷达1与雷达4仍有部分信号被误分选为普通雷达信号.
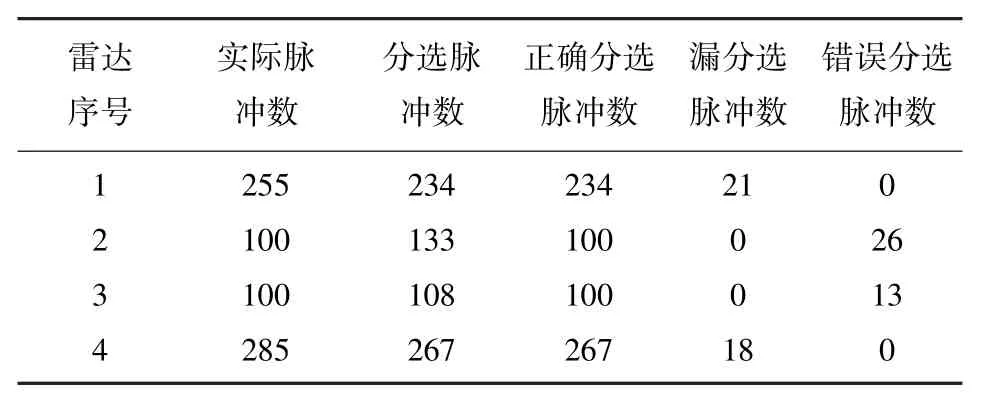
表3 基于Kohonen网络模型的聚类算法分选结果
2 基于云模型的分选结果有效性评估算法
由于雷达辐射源都存在固有参数,对多模雷达信号进行分选时同一部雷达的脉冲序列相比于不同辐射源的脉冲序列相似性更高.因此,在利用基于数据场的层次聚类对多模雷达信号进行处理后,引入云模型来对分选结果进行分析,可对处于一部雷达的多种工作模式下的雷达信号进行相似度判定[10],根据提出的评估确定是否将其归为一部雷达辐射源.
2.1 云的基本概念
云模型是一种可以描述自然语言和数据挖掘领域中未知概念的模糊性和随机性的数学工具[11].设U是一个用精确数值表示的论域(可以是一维的、二维的或多维的),C是U上的定性概念,U中的元素x对于T所表达的定性概念是一个具有稳定倾向的随机数,x在论域上的分布称为隶属云,简称为云.U在[0,1]取值,云是从论域U到区间[0,1]的映射,其中每一个x称为每一个云滴[3].
云的数字特征包括期望Ex,熵En和超熵He三种特征参量,它们反映了定性概念在整体上的定量特征.期望Ex在数域中代表所有数据的重心位置,可以认为它是一个定性的概念点.熵En在数域中可以理解为可接受的数值散度的范围,代表了数域中定性概念的不确定性.超熵He是熵En的熵,在数域中代表数据的凝聚性,是定性概念的不确定性度量[3].
2.2 基于云模型的分选结果评估算法
2.2.1 云模型隶属度计算
求取云模型隶属度作为相似度判定参数.云模型隶属度计算的基本思想为:首先对基于数据场的层次聚类分选后的每个聚类分别根据逆向云模型发生器建立云模型,然后根据正向云模型发生器分别求取其他聚类对该云模型的稳定倾向度,即隶属度.
将聚类分选结果中的每个辐射源都看作一个定性概念,设第i个聚类的信号样本为xijk,i=1,2,…,m,j=1,2,…n,k=1,2,3,其中m是分选结果中雷达辐射源的数目,n为每个雷达辐射源中信号样本的数目,k代表每个信号样本的特征参数个数.选取RF、PW、DOA三参数作为分选向量,因此k=3.设xij1为载频样本,xij2为脉宽样本,xij3为脉冲到达方向样本.根据涉及的不需要确定度信息的逆向云发生器算法[12],求取构成多维云模型各维度的特征参数Exk、Enk和Hek:
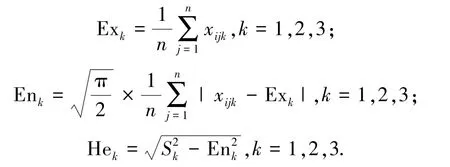
根据正向云模型发生器原理[11],生成针对其雷达辐射源信号的多维云模型.以Enk为期望,以为方差生成正态随机数为

进而生成三维云模型
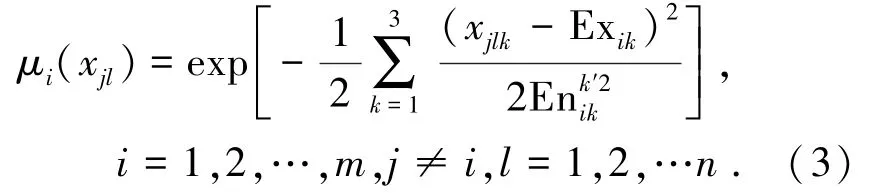
式中:μi(xjl)代表分选结果中的第j个聚类结果中第l个信号样本对第i个聚类结果构成的云模型的隶属度,xjlk是第j个聚类结果中第l个信号样本,n是第j个聚类结果中信号样本的个数,Exik表示第i个聚类结果中第k维特征的期望值.
式(3)可以表征其他聚类结果中信号样本对某聚类结果构成的多维云模型的相似度.从云模型理论分析,该式表征的是信号样本对某聚类结果抽象成的定向概念的隶属度.利用式(3)求取每个聚类结果中所有信号样本对其他聚类结果的隶属度均值Eμij:
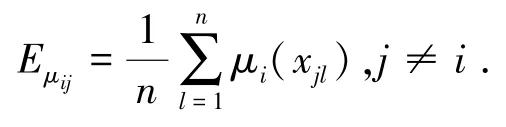
2.2.2 分选结果评估准则
当多模雷达信号分选时,在得到不同聚类结果之间的隶属度均值后,设定分选结果判定规则:
1)利用第i个聚类与第j个聚类的云模型数字特征(Exi,Eni,Hei),(Exj,Enj,Hej),采用自适应阈值生成方法[13]确定阈值εμ.
2)当第i个聚类与第j个聚类的隶属度均值Eμij大于阈值εμ时,比较两个聚类结果的ExDOA的差值Δ=|ExDOA(i)-ExDOA(j)|,若差值Δ小于设定阈值εdoa,则认定这两个聚类为同一雷达辐射源信号的不同工作模式.
3)若第i个聚类与第j个聚类的隶属度均值Eμij大于阈值εμ,且DOA均值的差值Δ大于设定阈值εdoa,说明该两个聚类并不来自同一辐射源,却具有较大的聚类相似度,则雷达信号多参数分选过程中的参数设定不是最优,将该隶属度均值反馈到多参数信号分选环节,用于聚类分选的参数优化.
4)若第i个聚类与第j个聚类的隶属度均值Eμij小于阈值εμ,则雷达信号得到了正确度较高的多参数分选,可将分选结果直接传输到雷达信号识别环节和威胁等级判定环节.
具体实现的流程图如图7所示.
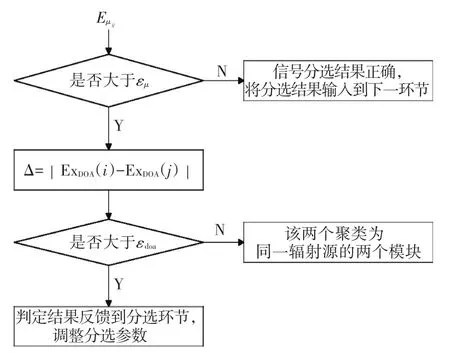
图7 分选结果有效性评估准则
2.3 仿真实验分析
为验证基于云模型的分选结果评估算法的有效性,利用基于数据场的层次聚类算法分选结果进行仿真实验.
从表2中分选结果可知,雷达1和雷达4的一部分多模雷达信号被误分选为雷达2与雷达3的辐射源信号.在采用分选结果评估算法进行处理后,雷达2与雷达3的聚类结果不符合分选有效性评估准则,将分选结果反馈到了层次聚类环节,对层次聚类的参数进行了修改,重新进行了计算,分选结果如图8所示.

图8 经分选结果评估算法反馈优化参数后分选处理结果二维显示图
经基于云模型的分选结果有效性评估算法反馈优化层次聚类参数后,分选结果出现了较大改进,如表4所示.

表4 经分选结果评估算法优化参数后基于数据场的层次聚类算法分选结果
基于云模型的分选结果有效性评估算法可准确有效评估多参数信号分选结果,并可反馈优化多参数分选算法的参数.应用于多模雷达信号分选中时,可判别聚类结果是否属于同一辐射源的不同工作模式,避免“增批”现象的出现,大幅度提高了雷达信号分选过程的准确性和分选结果的可靠性,具有较高的实用价值.
3 结 论
1)针对传统分选算法不能有效处理多模雷达信号问题,提出基于数据场的层次聚类多参数分选算法,利用数据场势函数的构建描述雷达信号数据的空间分布,通过等势线的绘制完成信号的自组织层次聚类.
2)针对聚类算法类间分离能力较差的问题,提出基于云模型的雷达信号分选有效性评估体制,利用云模型可以从小数据样本总结出带有不确定性定性概念的特点,将多参数分选结果中的每个聚类看作定性概念,采用逆向云模型发生算法生成云模型,计算每个聚类与其他聚类的平均隶属度值,根据分选结果评价规则处理分选结果.
3)仿真实验证明,提出的分选结果评价算法可有效减少多模雷达信号分选过程中“增批”现象的出现,并能有效对信号分选参数进行优化,进而增加了信号分选准确率.
[1]何明浩.雷达对抗信息处理[M].北京:清华大学出版社,2010:4-100.
[2]赵玉,陆志宏.一种多模雷达信号分选方法的研究[J].现代电子技术,2010,33(13):99-102.
[3]曲卫,刘孝刚,潘显俊.神经网络在电子对抗与反对抗中的应用[J].计算机与网络,2011(34):271-272.
[4]国强,王常虹,李峥.支持向量聚类联合类型熵识别的雷达信号分选方法[J].西安交通大学学报,2010,44(8):63-67.
[5]聂晓伟.基于K-Means算法的雷达信号预分选方法[J].电子科技,2013,26(11):55-58.
[6]王军,张冰.基于动态网格密度聚类的雷达信号分选算法[J].现代电子技术,2013,36(21):1-4.
[7]李德毅,杜鹢.不确定性人工智能[M].北京:国防工业出版社2005:190-210.
[8]王树良.基于数据场与云模型的空间数据挖掘和知识发现[D].武汉:武汉大学,2002.
[9]郭杰,陈军文.一种处理未知雷达信号的聚类分选方法[J].系统工程与电子技术,2006,25(6):853-856.
[10]李海林,郭崇慧,邱望仁.正态云模型相似度计算方法[J].电子学报,2011,39(11):2561-2567.
[11]李德毅,刘常昱.论正态云模型的普适性[J].中国工程科学,2004,6(8):28-34.
[12]李德毅,知识表示中的不确定性[J].中国工程科学,2000,2(10):73-79.
[13]张家精,王焕宝,倪友聪,等.云模型的隶属概念判定中阈值生成[J].计算机工程与应用,2011,47(24):125-128.
(编辑王小唯)
The research of sorting method for multimode radar signal based on data field and cloud model
GUO Qiang,SONGWenming,NAN Pulong,WAN Jian
(College of Information and Communication Engineering,Harbin Engineering University,150001 Harbin,China)
To solve the problem that traditional sorting methods can not effectively deal with multimode radar signals,a new signal sorting method based on date field and hierarchical clustering is proposed to avoid the appearance of increasing-batch phenomenon when sortingmultimode radar signals,and then a new algorithm based on cloud model used to evaluate the effectiveness of sorting results without database of radar radiation source is presented.The proposed algorithm is verified by simulations.
multimode radar;data field;cloud model;radar signal sorting
TN974
:A
:0367-6234(2015)11-0076-06
10.11918/j.issn.0367-6234.2015.11.013
2014-03-25.
国家自然科学基金(61371172,61240007);黑龙江省科技攻关(GC13A307);黑龙江省博士后科研启动金资助(LBH-Q12122);海洋工程国家重点实验室基金(1213);哈尔滨市应用技术与开发(2013RFJGJ009).
国 强(1972—),男,博士,教授.
南普龙,npl1108@163.com.

