基于加性噪声模型的基因调控网络构建算法
王春宇,宋建春,郭茂祖,邢林林,刘晓燕
(哈尔滨工业大学计算机科学与技术学院,150001哈尔滨)
基于加性噪声模型的基因调控网络构建算法
王春宇,宋建春,郭茂祖,邢林林,刘晓燕
(哈尔滨工业大学计算机科学与技术学院,150001哈尔滨)
为在统计推断方法通过相关性来筛选基因对时,能够体现调控关系的因果性,受因果定向算法能够有效定向调控关系的启发,将加性噪声模型与因果定向算法相结合,用基于加性噪声的定向算法度量因果关系的程度,提出了一种基因调控网络构建的算法.该算法首先将加性噪声模型的因果定向算法扩展为一个特征选择算法,并通过建立调控因子集合与每个基因间的加性噪声模型来选择基因的调控因子.在DREAM5的3个数据集上的实验结果显示,结果比其他算法有明显提升,该算法可有效构建基因调控网络.
加性噪声模型;因果定向;基因调控网络;特征选择
基因调控网络构建算法通过基因表达的观测数据发现基因间的调控关系,调控网络有助于理解生物基因转录、翻译的深层调控机制,同时,基因调控网络的变化能够体现细胞分化和癌症生成等生物现象.由于生物体是一个复杂的有机体,基因在生物体中并不是孤立的,基因之间的相互作用非常复杂.这种作用表现为一个基因的表达受其它基因直接或间接影响,同时又影响其它基因的表达,这种相互影响与制约的关系构成了复杂的调控网络.
基因调控网络构建算法常用DNA基因表达微阵列数据.DNA微阵列是一种能够快速、高效检测DNA片段序列、基因型多态性或基因表达水平的技术,可并行检测上千万个基因的活动,通过检测mRNA水平来指示基因表达情况.
利用基因表达数据和调控因子信息,本文提出一种基因调控网络构建算法,该算法将基于加性噪声模型ANM(additive noisemodel)的因果定向算法扩展为特征选择算法,以此构建调控网络.该算法的特点是利用加性噪声模型得到的噪声变量与自变量的相关性来选择特征,即基因的调控因子,以降低的假阳性.结果表明基于加性噪声模型的因果算法可以反映变量间因果关系的程度,通过扩展的特征选择算法在一定程度能够提取变量的原因变量,在基因调控网络构建问题中,表现为能够提取出基因的受调控因子.
1 相关研究
1.1 基因调控网络构建算法
目前,已有很多模型和方法用于构建基因调控网络,文献[1]从模型构建的角度对这些方法进行总结和比较.主要的调控网络构建模型包括逻辑模型、微分方程模型和贝叶斯模型等.文献[1]提出的布尔模型,将基因间相互作用理解为逻辑规则,但只能定性地描述调控网络,很难准确描述基因间的复杂关系.文献[2]用线性常微分方程来描述网络系统,能定量的表示调控网络的复杂关系,但缺乏抗噪声能力,且计算量较大.贝叶斯网模型可作为上述两种方法的折中,其原本就表示不确定事物的相互作用,可用来表示复杂的基因调控关系,而且能自然融入先验知识.文献[3]用爬山法和BDe评分函数学习酵母细胞周期的调控网络,并用“sparse candidate”减小搜索空间.为更好的描述调控关系的动态特征,文献[4]引入动态贝叶斯模型(DBNs),理论分析DBNs从时序基因表达数据中学习调控网络的问题.贝叶斯网虽能够较精确的描述调控网络,但时间复杂度高,无法构建大规模网络.文献[5]从统计推断的角度分析和比较了基因调控构建算法,根据所用统计量的不同,将统计推断方法分为基于相关性和基于互信息两类.
统计推断构建基因调控网络的基本思路是:计算每对基因间的相关性或互信息,通过阈值筛选统计显著的基因对,并认为具有调控关系.如Relevance Network算法[6]和互信息快速算法[7]等.为提高构建网络的精度并降低假阳性,Aracne算法[8]利用了DPI(data processing inequality)过滤假阳性的调控关系;CLR算法[9]利用自适应的阈值选择方法,通过背景分布筛选基因;C3NET(conservative causal core)算法[10]选各基因最显著连接为调控网络的边.统计推断方法假设基因间的相关性反映调控关系,准确的说,基因间的调控关系是调控因子表达量与基因表达量的一种因果关系,即调控因子是被调控基因表达量的原因.统计学认为相关关系不等价于因果关系,所以有必要研究以因果关系为基础的基因调控构建算法.
值得一提的是,很多基因调控网络构建算法来自DREAM(dialogue on reverse engineering assessment andmethods)计划[11],其目标是促进系统生物学的分子网络推导、加强定量模型构建与实验的相互作用.该计划通过实验数据来推导分子网络并构建定量模型,再利用这些网络和模型来指导实验,将理论与实验相结合.文献[11]总结DREAM5中出现的各种调控网络构建算法,并使用几个标准数据集比较和分析不同的算法,并通过主成分分析法说明几类方法的不同偏向.
研究表明[12],基因的表达由一些特殊的蛋白质转录因子控制,转录因子形成美杜莎结构(medusa structure)调控基因网络.因此,结合物种的转录因子信息,可将基因调控网络的构建问题简化成每个基因的调控因子选择问题.如果将物种已知的调控因子作为特征,基因调控网络构建就是对每个基因做特征选择,筛选出其调控因子. TIGRESS[13]利用Lasso回归作为特征选择方法,并采用bootstrap抽样克服Lasso选择的不稳定性;GENIE3[14]通过训练以调控因子为节点的随机森林预测目标基因的表达水平,根据构建的随机森林构建基因调控网络.目前,大多数的特征选择算法是为了提高分类或回归模型的精度和泛化能力,而不是从因果关系的角度提取目标变量的原因变量,本文认为因果定向算法在某种程度上可用于提取原因变量.
1.2 基于加性噪声模型因果定向算法
因果定向算法的目的是识别两个观测变量的因果方向,最近几年已有相关模型和方法.可描述为:假设有观测变量X和Y,取值为连续或离散的,通过它们的观测值集合
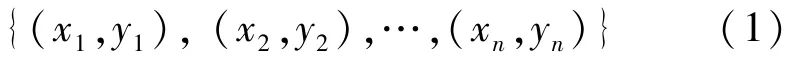
确定X和Y的因果关系.
现有的模型和方法假定:若cause为成因变量,effect为结果变量,那么观察数据联合概率分布p(cause,effect)沿因果方向(causal→effect)的分解p(cause)p(effect|cause)比其反方向(effect→causal)的分解p(effect)p(cause|effect)复杂度更低,可通过比较两个方向分解的复杂度来识别因果方向[15].
根据复杂度表示法的不同,可将模型分为两类.第一类通过独立性测试识别因果方向,如加性噪声模型[16]和PNL(post non-linear)方法[17].这两个模型都是通过检验假设的成因变量与噪声之间的独立性来判别因果方向,加性噪声模型通过回归获得噪声,而PNL利用了独立成分分析(ICA)技术.第二类定义复杂性度量,直接计算两个方向的复杂度.复杂度小的为因果方向,包括GPI方法[18]和IGCI(information geometric causal inference)方法[19].GPI方法利用贝叶斯网络作为因果产生的机制,通过计算网络的复杂性识别因果方向,而IGCI方法通过相对熵来计算因果关系的复杂性.研究表明因果定向算法可较为准确的判别基因间的调控方向[15],由于很多现有的基因调控网络构建算法对调控方向没有判别性,因此利用因果定向算法可对预测的调控关系定向.
基于加性噪声模型的因果发现模型假设因果关系的产生过程为
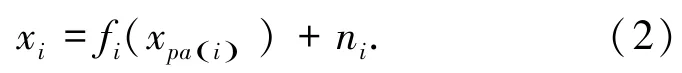
式中:xi为观测变量,ni为其双亲节点的函数加上相互独立的噪声变量,fi为任意函数.
在满足一定条件下,加性噪声模型可判断观测变量X、Y间的因果关系.首先,测试两变量间的统计独立性,若相互独立则说明两变量间不存在因果关系.其次,若不相互独立,则测试模型Y=f(X)+n是否和数据一致,方法是检验通过非线性回归分析得到的噪声变量n是否和X相互独立,如果相互独立则认为是一致的,否则不一致.如果一致,则接受该模型,即X→Y的因果关系成立.如果两方向的模型均不成立,则两个观测变量没有因果关系.
2 基于ANM基因调控网络构建算法
受到因果定向算法能够有效定位基因调控关系的启发,本文认为基因间的调控关系可用因果定向算法度量,通过计算每个基因对因果方向的复杂性可识别出调控关系.
假设调控因子调控基因表达的过程符合加性噪声模型,通过检验观测数据与模型的一致性来判别调控关系.构建调控因子与基因间的ANM模型,并用模型得到p-value作为调控关系强弱的表示,利用阈值筛选出预测的显著调控关系.但是,基因调控关系复杂,每个基因的调控因子可能有多个,单纯的考虑基因与单调控因子间的作用不够准确,需要同时考虑多调控因子对基因的作用.本文的方法是建立式(3)所示所有调控因子与基因间的ANM模型.然后通过算法检验每个调控因子与噪声变量n的独立性来筛选调控因子.
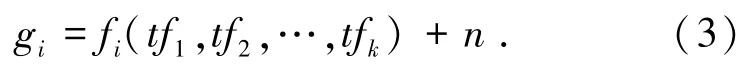
算法如下.
输入:基因表达数据D(行为实验,列为基因),基因索引数组G,调控因子索引数组TFs(基因表达数据的索引),自定义阈值T.
输出:基因调控关系集R
begin
1.将G划分为TFs和非调控因子索引数组non -TFs;
2.对D的每列规范化,使每列均值为0、L1-范数为1,即(i为列号);
3.初始化集合R=Ø
4.for each g∈G do
5.建立所有调控因子与g的ANM模型,即

如果构建网络的基因数为N调控因子数为M时,需要构建N次ANM模型和M×N次独立性检验,而由ANM模型中回归算法获得噪声变量的复杂性,可得算法1时间复杂度是N次回归与M×N次独立性检验之和.
当用两个成因变量的ANM模型分析时,该模型为
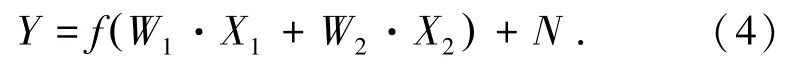
利用皮尔森相关系数说明变量间的独立性,并归一化变量X1、X2和Y,使E(X1)=E(X2)=0,,那么归一化后变量的相关系数等于两变量的余弦值,另外假设函数f为简单的线性函数,即N=Y-W1X1-W2X2,那么
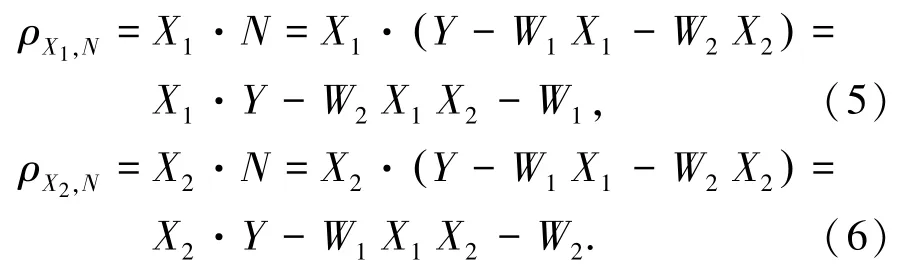
其中,ρX1,Y=X1·Y,ρX2,Y=X2·Y,上述两个相关性比值为
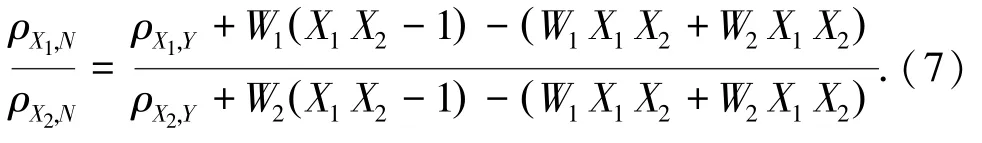
3 实验与分析
3.1 实验数据
实验数据见表1,采用3个数据集,均来自DREAM5,包括由GNW(gene net weaver)[20]生成的模拟数据集、酵母细胞和大肠杆菌数据集,包括用于构建调控网络的基因表达数据集和用于验证的调控关系数据集,调控关系数据指定了基因间验证过的调控关系.另外,还有对应的调控因子数据库,结合已知的调控因子,可降低程序运行时间和提高预测的精度.
GNW是第一个能够生成模拟基准和分析网络推导算法性能的工具,很容易生成基因调控网络的精细模型.相对于活体的实验,GNW能够快速和简单的产生表达数据,而且其数量和质量能够得到控制.大肠杆菌调控关系验证数据来自RegulonDB(version 6.4)数据库,这些调控关系主要是通过手工从文献中检索,Chip-qPCR数据显示RegulonDB具有85%的完整性.酵母细胞的验证数据集通过在ChIP-on-chip数据集定位启动子序列.
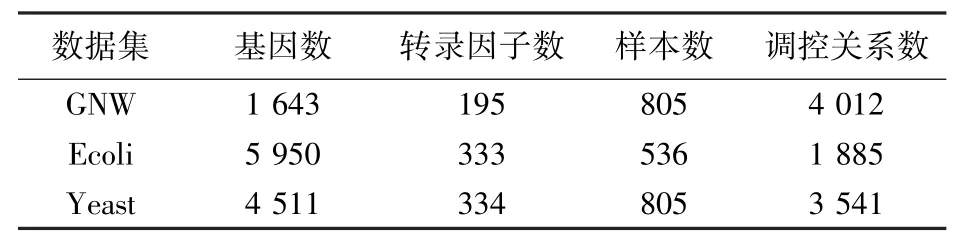
表1 实验数据集
3.2 实验方法与评价
实验分别用Lasso回归和SVR(support vector pegression)回归构建ANM模型,用LARS算法[21]求解Lasso回归模型,用libsvm工具包[22]求解SVR回归,用皮尔森相关系数计算变量间的相关性.
Lasso回归是一种收缩和选择方法,给定一组输出变量Y的观测值和输入变量X1,X2,…,Xp的观测值,优化线性模型为
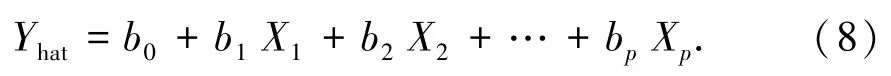
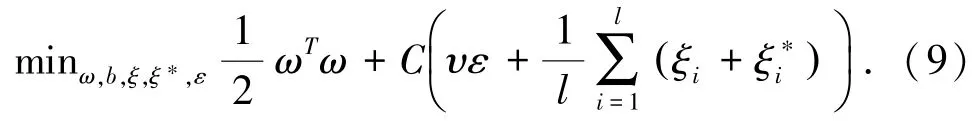
且满足(ωTφ(xi)+b )-zi≤ε+ξi和zi-其中1,…,l).实际上不直接求解该优化问题,而是通过转化成对偶问题来求解.
实验结果用ROC曲线及AUROC来说明算法的效果,首先定义两个变量RTP(true position rate)和RFP(false position rate),分别定义为RTP= NTP/(NTP+NFN)和RFP=NFP/(NFP+NTN),其中NTP和NFN分别为预测正确和错误的调控关系数,NTN和NFP分别为预测正确和错误的非调控关系数.
通过设定不同阈值,获得不同阈值条件下的RTP和RFP,根据这些数据绘制ROC曲线,并计算ROC曲线下的面积AUROC.为说明算法的有效性,给出了两个对比实验.
1)说明加性噪声模型得到的p-value可作为调控关系的度量,建立每个调控因子与目标基因的ANM模型,并计算p-value作为之间调控关系的度量,通过阈值筛选出显著的调控关系,并与多调控因子对目标基因的ANM模型比较.
2)用Lasso和SVR实现了ANM模型,并与asso回归和皮尔森相关系数方法进行比较,皮尔森相关系数方法是计算每对调控因子与非调控因子的皮尔森相关系数,再通过阈值筛选出相关性比较大的基因对作为预测,而Lasso回归选择对应回归系数不为零的调控因子作为目标基因的调控因子.
3.3 实验结果与分析
实验一的ROC曲线位于y=x上方如图1说明单个调控因子与目标基因的p-value作为度量是可以的,并且所有的调控因子的ANM模型(All TFs)比单个ANM模型(Single TF)能更准确的度量调控关系.由实验二的ROC曲线(见图2)和AUROC结果(见表2),可看出基于ANM的特征选择方法比Pearson和Lasso特征选择的预测效果好,模拟数据GNW上ANM效果比Pearson方法差,而且Lasso方法比Pearson方法差,说明ANM能够提高Lasso特征选择的能力,其中在Ecoli数据集上,本文方法提高的效果很明显.
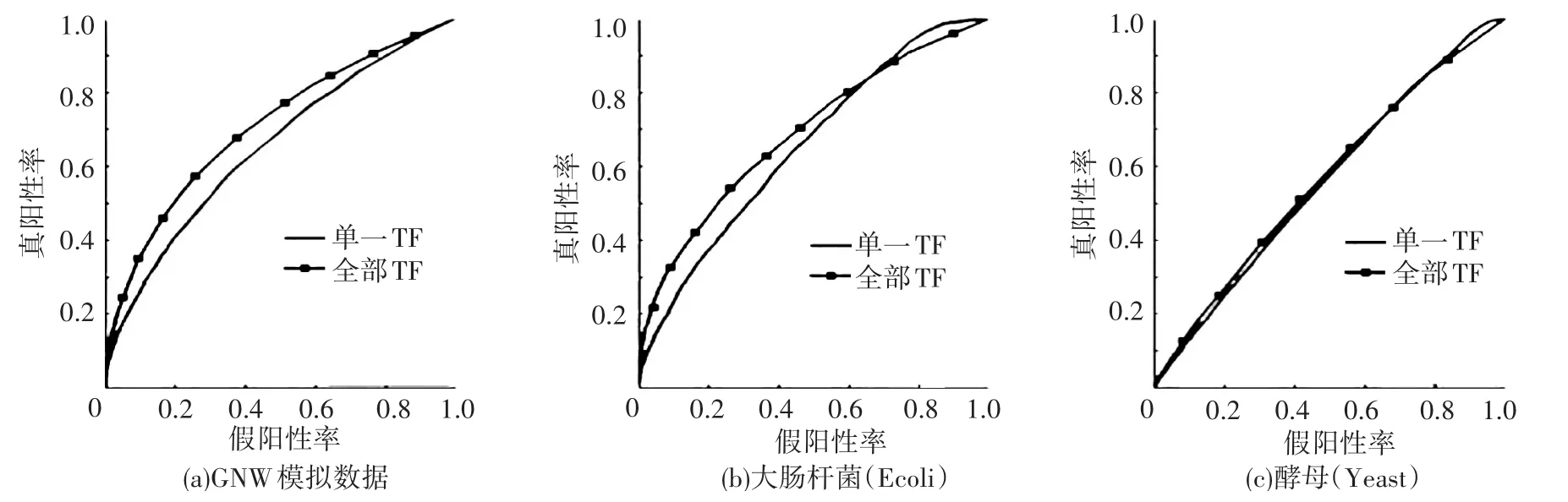
图1 单调控因子与多调控因子作用
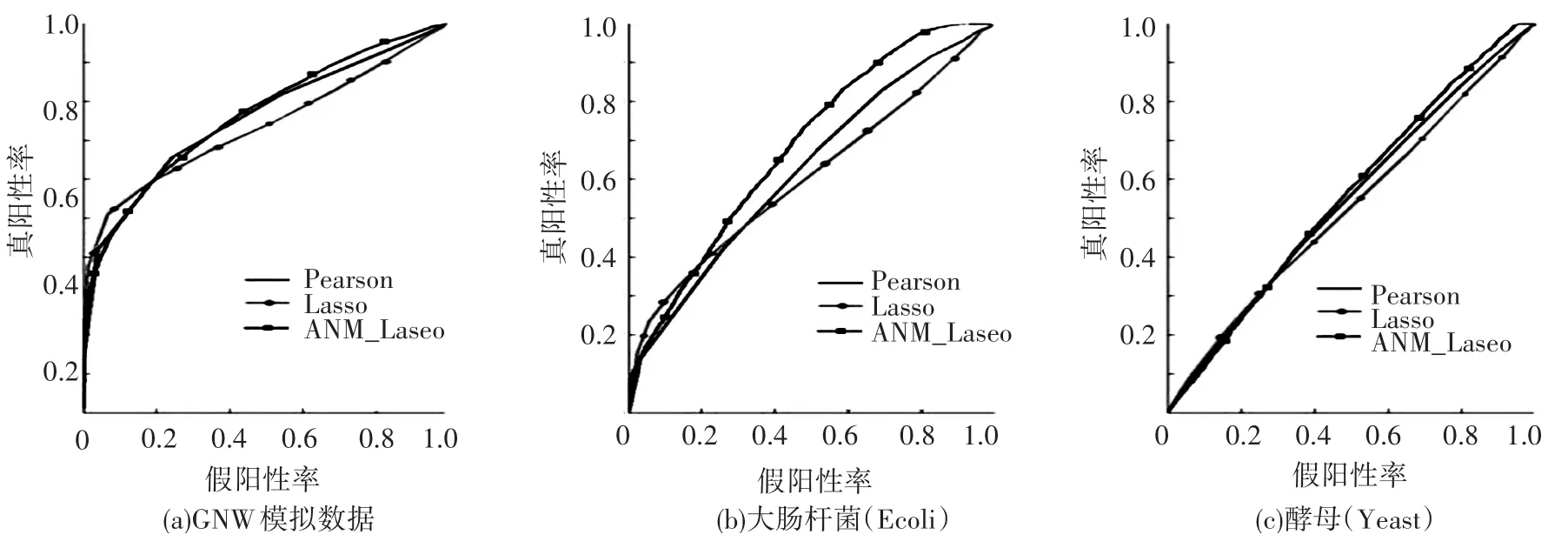
图2 基因调控网络构建方法的ROC曲线比较实验
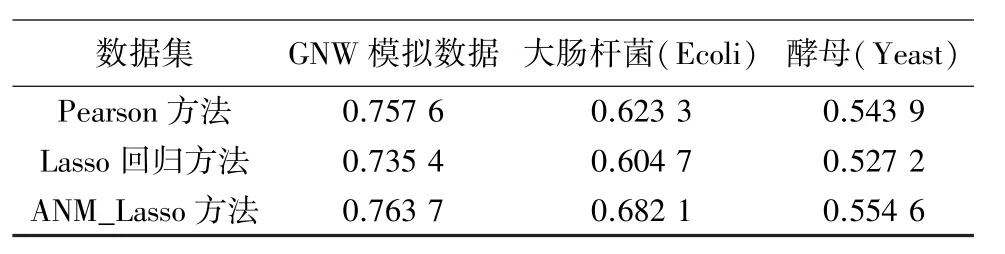
表2 基因调控网络构建方法的AUROC
4 结 语
本文在加性噪声模型的基础上,提出基于加性噪声的特征选择,并用该算法构建基因调控网络,算法将加性噪声模型中产生的p-value作为因果强度的度量,而不仅仅是判别因果方向.为了综合多个调控因子的作用,本文扩展该模型,适用于多个调控因子与目标基因的加性噪声模型,实验结果表明,这样做能够提高预测的效果.将改进后的多调控因子的加性噪声模型与皮尔森相关系数和Lasso方法比较,在ROC曲线上和AUROC上可以看出本文方法比后两种方法好.对此,本文给出相关的理论解释,公式推导的结果看出多调控因子的加性噪声模型综合了目标基因与调控因子的皮尔森相关系数和回归系数的作用.当然,这种解释不够精确,需要进一步说明超参数对权值的影响.
[1]KARLEBACH G,SHAMIR R.Modelling and analysis of gene regulatory networks[J].Nature Reviews Molecular Cell Biology,2008,9(10):770-80.
[2]CHEN T,HE H,CHURCH M.Modeling gene expression with differential equations[C]//Pacific symposium on biocomputing.Hawaii,USA:UC San Francisco,1999:4-16.
[3]FRIEDMAN N,LINIAL M,NACHMAN I,et al.Using Bayesian networks to analyze expression data[J].Journal of computational biology,2000,7(3/4):601-20.
[4]MURPHY K,SAIRA M.Modelling Gene Expression Data Using Dynamic Bayesian Networks[R].Technical report,Berkeley:Computer Science Division University of California,1999.
[5]EMMERT-STREIB F,GLAZKO G,DE MATOS SIMOES R,et al.Statistical inference and reverse engineering of gene regulatory networks from observational expression data[J].Frontiers in genetics,2012,3:8-23.
[6]BUTTE A,KOHANE I.Mutual information relevance networks:functional genomic clustering using pairwise entropymeasurements[C]//Pac Symp Biocomput.Stanford USA:Stanford University,2000:418-429.
[7]QIU P,GENTLES A,PLEVRITIS S.Fast calculation of pairwise mutual information for gene regulatory network reconstruction[J].Computer methods and programs in biomedicine,2009,94(2):177-180.
[8]MARGOLIN A,NEMENMAN I,BASSO K,et al. ARACNE:an algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context[J]. BMC Bioinformatics,2006,7(Suppl 1):7-22.
[9]FAITH J,HAYETE B,THADEN J,et al.Large-scale mapping and validation of Escherichia coli transcriptional regulation from a compendium of expression profiles[J]. PLoS biology,2007,5(1):8-21.
[10]ALTAY G,EMMERT-STREIB F.Structural influence of gene networks on their inference:analysis of C3NET[J]. Biol Direct,2011(6):31-47.
[11]MARBACH D,COSTELLO J,et al.Wisdom of crowds for robust gene network inference[J].Naturemethods,2012,9(8):796-804.
[12]GUO Y,FENG Y,TRIVEDIN,et al.Medusa structure of the gene regulatory network:dominance of transcription factors in cancer subtype classification[J].Experimental biology and medicine,2011,236(5):628-636.
[13]HAURY A,MORDELET F,VERA-LICONA P,et al. TIGRESS:Trustful Inference of Gene REgulation using Stability Selection[J].BMC systems biology,2012,6(1):145-162.
[14]IRRTHUM A,WEHENKEL L,GEURTS P.Inferring regulatory networks from expression data using tree-based methods[J].PloS one,2010,5(9):12776-12786.
[15]STATNIKOV A,HENAFF M,LYTKIN N,et al.New methods for separating causes from effects in genomics data[J].BMC Genomics,2012,13:(Suppl 8):22-38.
[16]HOYER P,DOMINIK J,MOOIJJ,etal.Nonlinear Causal Discovery with Additive Noise Models[C]//In Advances in Neural Information Processing Systems.Vancouver,Canada:NIPSFoundation,2009:689-96.
[17]ZHANG K,HYVÄRINEN A.Distinguishing causes from effects using nonlinear acyclic causalmodels[C]//Journal of Machine Learning Research,Workshop and Conference Proceedings(NIPS 2008 causality workshop). Vancouver,Canada:NIPS Foundation,2008:157-164.
[18]STEGLE O,DOMINIK J,ZHANG K,et al.Probabilistic Latent Variable Models for Distinguishing between Cause and Effect[C]//In Advances in Neural Information Processing Systems.Granada,Spain:NIPS Foundation,2010:1687-95.
[19]JANZING D,MOOIJ J,ZHANG K,et al.Informationgeometric approach to inferring causal directions[J]. Artificial Intelligence,2012,182:1-31.
[20]SCHAFFTER T,MARBACH D,FLOREANO D. GeneNetWeaver:in silico benchmark generation and performance profiling of network inference methods[J]. Bioinformatics,2011,27(16):2263-2270.
[21]EFRON B,HASTIE T,JOHNSTONE I,et al.Least angle regression[J].The Annals of statistics,2004,32(2):407-499.
[22]CHANG C,LIN C.LIBSVM:a library for support vector machines[J].ACM Transactions on Intelligent Systems and Technology(TIST),2011,2(3):27-66.
(编辑苗秀芝)
Additive noisemodel based gene regulatory network construction algorithm
WANG Chunyu,SONG Jianchun,GUO Maozu,XING Linlin,LIU Xiaoyan
(School of Computer Science and Technology,Harbin Institute of Technology,150001 Harbin,China)
In order to represent causal relationship when relevancemeasure is used in statistic inferencemethods to filter gene pair,inspired by the research that casual-effect orientation algorithm can identify direction of causaleffect variables effectively,we propose an additive noise model based on the gene regulatory network construction algorithm by using additive noisemodel orientation algorithm tomeasure degree of causal relationship.The algorithm extends additive noisemodel based orientation algorithm to a feature selective algorithm,and builds ANM model of transcription factors set and each gene to select transcription factors of gene.In the experiments of three datasets DREAM5,the method has clear improvement in comparison with other algorithms,and could be used as an efficient algorithm to build gene regulatory networks.
additive noisemodel;causal-effect orientation;gene regulatory network;feature selection
TP391
:A
:0367-6234(2015)11-0022-05
10.11918/j.issn.0367-6234.2015.11.004
2014-09-26.
国家自然科学基金(913351122,61172098,61271346,61402132);高等学校博士学科点专项科研基金氏族12302110040);中央高校基本科研业务费专项资金(HIT.KISTP. 201418).
王春宇(1979—),男,博士研究生,讲师;郭茂祖(1966—),男,教授,博士生导师.
王春宇,chunyu@hit.edu.cn.

