同时射击时反坦克导弹视场交叉数学模型研究*

魏现杰，姜增良，张彦朴，邵云峰

（南京炮兵学院廊坊校区，河北 廊坊 065000）

同时射击时反坦克导弹视场交叉数学模型研究*

魏现杰，姜增良，张彦朴，邵云峰

（南京炮兵学院廊坊校区，河北 廊坊 065000）

反坦克导弹同时射击时测角视场交叉可能引起导弹失控，针对此问题，利用信息系统的位置地理信息，参照装备的基本性能参数，构建了配置阵地的数学模型，得出了同时射击的可行性判据，为阵地射击指挥提供了决策支持。

反坦克导弹，视场交叉，数学模型，判据

0 引言

反坦克导弹在同时射击时，阵地配置不当可能造成测角仪视场的交叉，造成制导装置间的相互干扰，从而引发导弹失控。为了避免同时射击时导弹间相互干扰，指挥员必须熟悉装备基本性能，对阵地配置距离进行粗略估算。如果依托数字化战场信息系统的位置地理信息，结合反坦克导弹的战术技术参数，建立配置阵地的数学模型，分析和总结同时射击可行性判据，对干扰过程进行定量的计算，对于射击指挥有着重要的意义。

1 坐标信息的获取

本文中选择大地坐标系（OXYH）作为计算坐标系。大地坐标系（OXYH）规定为：反坦克导弹配置点D0作为坐标系原点O，OX轴规定为过原点与地球表面相切，导弹的攻击方向（一般指向目标M0）为正；OH轴：过O点的铅垂线，向上为正；

OY轴：过O点垂直于OXH平面，方向按照右手定则确定，如图1所示。

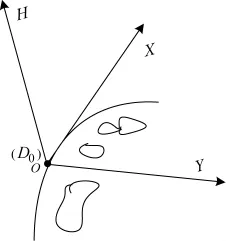
图1 坐标系OXYH的选择

要将战术地图上所呈现的坐标信息转化为坐标系OXYH的坐标，可以经过以下计算步骤：

第1步：将数字化地图的坐标原点平移到D0（x0''，y0''，h0''） 点，坐标系转化为过渡坐标系OX'Y'H'。导弹配置地点位置D0、D1、D2、…、Dm坐标变化为：（xn'，yn'，hn'）=（xn'-x0''，yn'-y0''，hn'-h0''）。目标位置M0、M1、…、Mn的坐标变化为：（am'，bm'，cm'）=（am'-x0''，bm'-y0''，cm'-h0''）

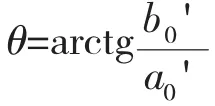
由坐标转移公式可得：

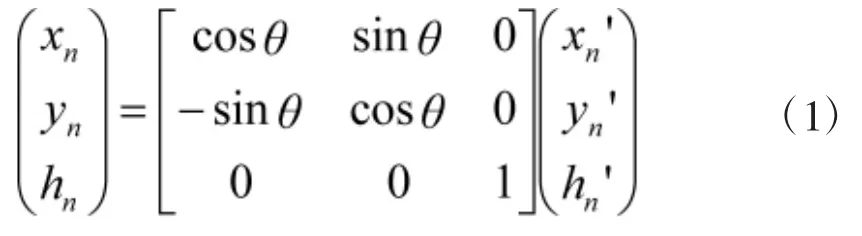
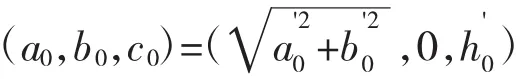
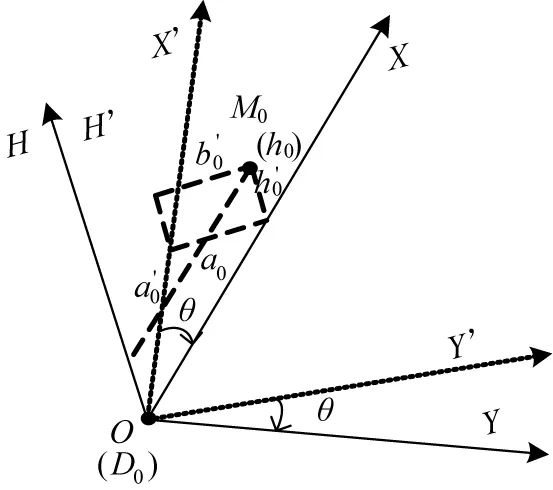
图2 坐标系0XYH的确立

在数字化战场上，反坦克导弹配置地点信息和目标信息可以实时显示到信息平台的指挥系统，辅助决策系统可以实时更新的目标信息，适时对坐标值进行数字化处理。当然，若两个直角坐标系OXYH和战术数字地图的纵轴、横轴不等比例，则必须先对OXYH坐标系进行归一化处理。使纵轴、横轴具有可比性。

2 视场交叉射击数学模型

两套同型号系统同时射击时，为了研究解决问题的一般性，假设：发射地点D0、D1，用（x0，y0，h0）、（x1，y1，h1）表示；目标的位置M0、M1，用（a0，b0，c0）、（a1，b1，c1）表示。

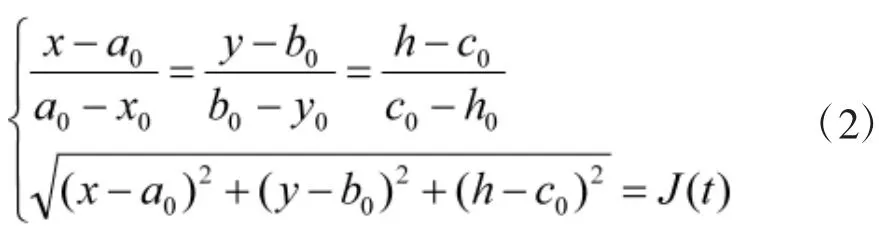
解得发射点D0发射后t秒的导弹坐标为：

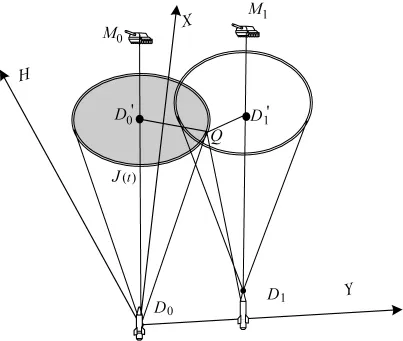
图3 两个同型号系统相互干扰动态过程分析（D0对D1干扰）

求得圆D0'内的任意一点Q，使得Q距离直线D1M1最近。因此，点Q需保证QD0'⊥D1M1。设Q（i，j，k），则QD0'⊥D1M1，QD0'⊥D0M0，∠QD0D0'=βt，建立方程组：

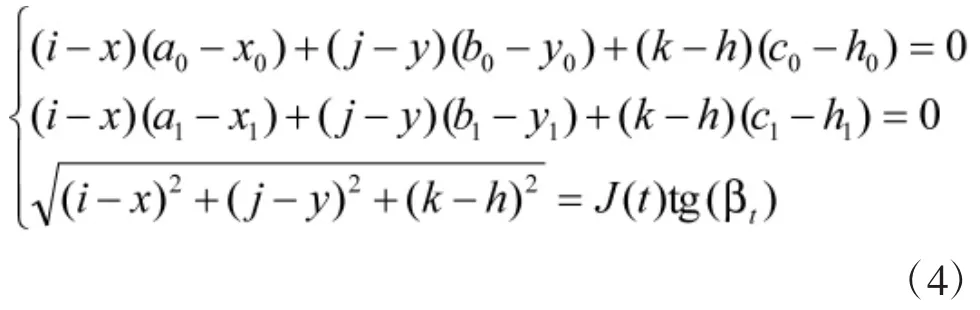
解得Q（i，j，k）的坐标为：

其中，

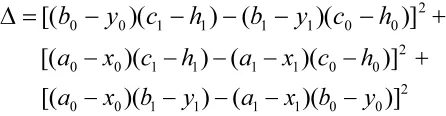
关于上式中正负号的取值有如下判据：

对于i，若（b0-y0）（c1-h1）-（b1-y1）（c0-h0）＞0取正值，反之，取负值。对于j，若（a0-x0）（c1-h1）-（a1-x1）（c0-h0）＞0取正值，反之，取负值。对于k，若（a0-x0）（b1-y1）-（a1-x1）（b0-y0）＞0取正值，反之，取负值。

综上计算，可以计算出

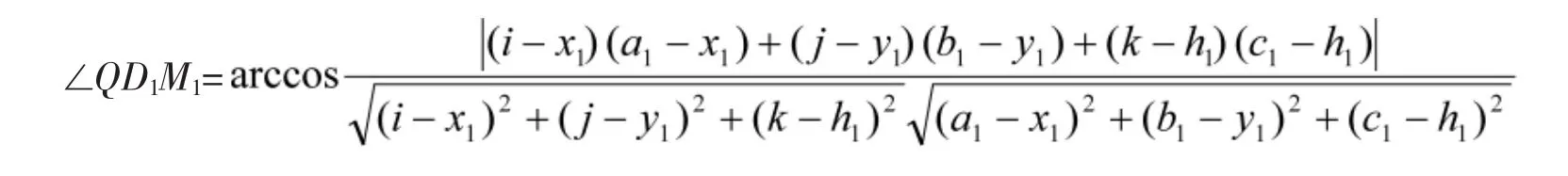
3 判据分析

反坦克导弹在发射初始阶段，为了有效捕获目标，采取大视场工作，但是为了保证中远距离的命中精度，有要求用小视场来有效提高测角精度。因此，设计时为了兼顾初始捕获窗口和小视场，反坦克导弹的测角视场变化一般都是逐渐减小的。反坦克导弹的最大半视场角用βmax表示，最小半视场角βmin表示。比较∠QD1D1'和βmax、βmin的大小是分析问题的关键。

若∠QD1D1'≥βmax，则D0发射地点的发射不会对D1发射地点的发射造成干扰。

若βmin＜∠QD1D1'＜βmax，则发射地点D0的发射可能会对发射地点D1的发射造成干扰，由于导弹的发射，其测量视场角β都是逐渐减小的，当β=∠－QD1D1'时，可以解得导弹D1的发射时间（即导弹发射t0后视场角β=∠QD1D1'）。要想导弹D0对导弹D1形不成干扰，则有可能可以按照时间间隔方式发射。要选择合理的时间间隔，首先应模拟导弹发射点D0发射程序（时间为0～T），计算导弹发射过程中观测视场角β小于∠QD1D1'的任意时间段（从时间T1至时间T2）。若（T1～T2）＞t0，则可以采取间隔发射的方式，发射时间点为；若（T1～T2）＜t0，则不允许同时发射。

若βmin＞∠QD1D1'，则发射地点D0的发射会对发射地点D1的发射造成干扰，不能同时发射。

4 算例与应用

假设条件：某两套（不同型号）反坦克导弹进行交叉射击，视场角第1套的配置点D0（x0，y0，z0）=（0，0，0，），第 2套的配置点为 D1（x1，y1，z1）=（25，150，50），目标M0（a0，b0，c0）=（2 500，0，-50），目标M1（a1，b1，c1）=（3 500，75，100），攻击方向分别为D0M0，D1M1。

根据基础条件分析：∠M0D0M1=arccos 0.998 59=3.04°＞βmin（第 1套最小视场角）；∠M0D1M1=arccos0.997 72=3.87°=67.5 mrad＞βmin（第2套最小视场角）。即不构成相互干扰的充分条件。

充分必要条件分析：首先，研究发射点D0对发射点D1的影响，根据式（3）～式（5）可以求出不同时间和距离上的视场边界点D0'（x，y，h）、Q（i，j，k），得出∠QD1D0'，如表1所示。由于∠QD1D0'的最小值≥βmax（第2套），即D0对D1的不构成干扰影响。

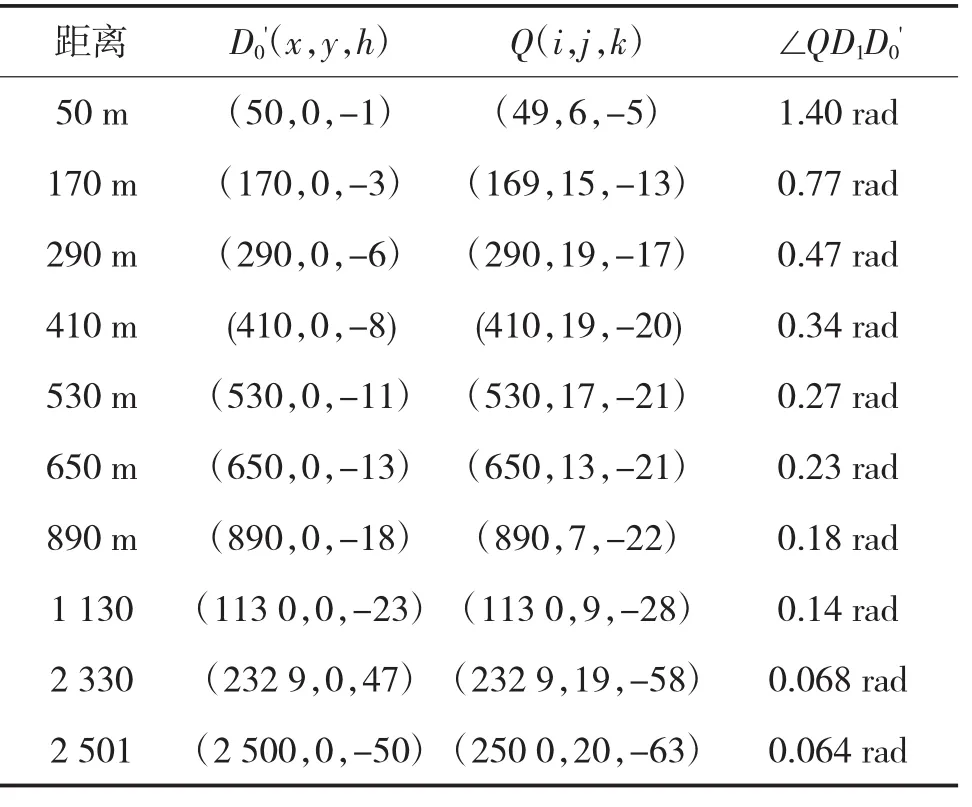
表1 D0对D1的干扰影响分析

同理，分析发射点D1对发射点D0的影响，求出视场边界点D1'（x，y，h）、P（i，j，k），得出∠PD0D1'，如表2所示。而βmin（第1套）＜∠PD0D1'＜βmax（第1套），即发射点D1可能对发射点D0构成干扰，通过分析第1套系统的视场变化规律，可以分析出当第1套系统发射出去x秒后，再发射第2套系统，不会产生干扰。

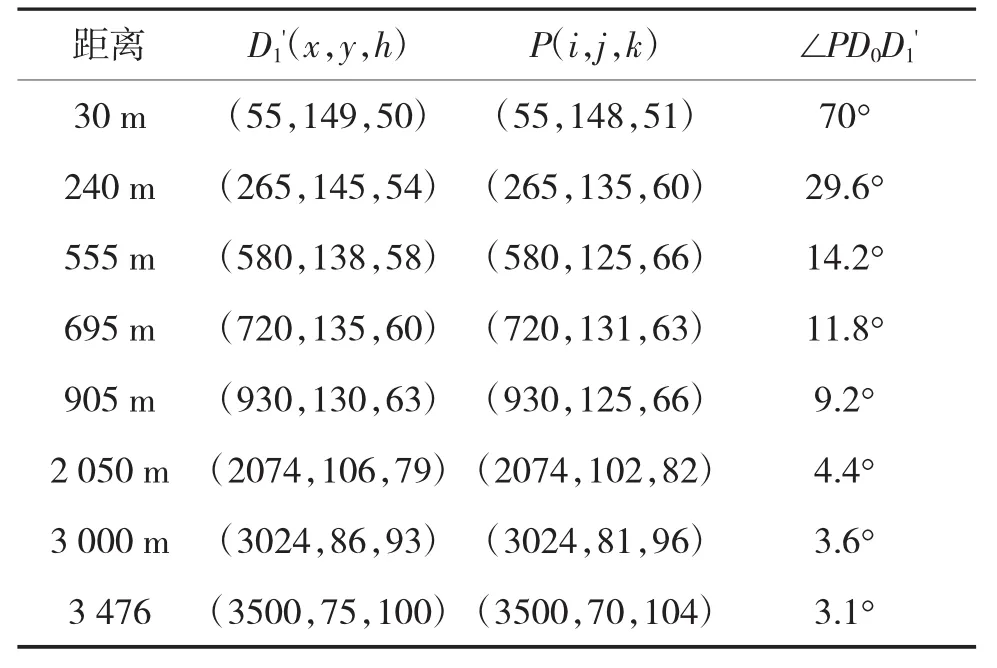
表2 D1对D0的干扰影响分析

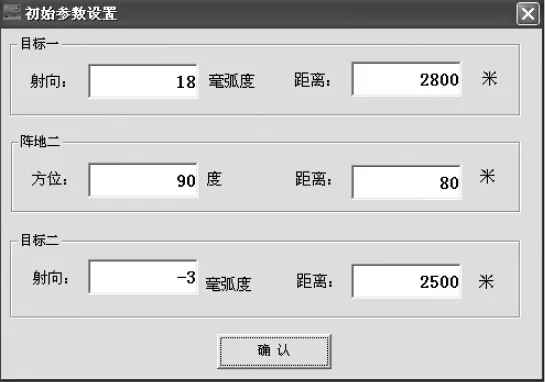
图4 输入界面

在反坦克导弹射击指挥信息系统中，利用该数学模型构建了指挥决策辅助软件，只需将导弹种类信息、各发射阵地位置信息和目标的位置信息作为输入变量，即可完成对多个阵地同时发射的可行性判断，如图4所示；对于红外干扰和其他干扰源信息，也可以将干扰源作为Q点进行干扰判别分析，判断为单个导弹发射阵地能否发射（是否干扰）。该模型充分利用了数字化战场的地理信息，自动形成初步判别结论，对于相互干扰的两个发射阵地，也可以方便地计算出发射顺序、发射间隔，该模型简练易行，对反坦克导弹射击的精确指挥决策有着重要的指导意义。

［1］张彦朴.反坦克导弹系统［M］.北京：解放军出版社，2012.

［2］关桐书.解析几何词典［M］.上海：上海教育出版社，1985.

［3］王涛，罗晓军.基于战术地图的GPS坐标定位［C］//北京：军事电子信息系统专题技术文选，2005.

［4］承继成，林晖，周成虎，等.海洋定位学［D］.大连:海军大连舰艇学院，2005.

Research on of Vision Intersection Mathematical Model of Simultaneous Firing of Anti-Tank Missile

WEI Xian-jie，JIANG Zeng-liang，ZHANG Yan-pu，SHAO Yun-feng
（Langfang Campus，Nanjing Artillery Academy of Chinese PLA，Langfang 065000，China）

Vision intersection of goniometers in simultaneous firing of Anti-Tank Missiles can cause to lose control of missile.Aiming at this problem，a mathematical model of firepower collocated position has been established，according to the information of geographic location and essential performable parameters of missiles.Feasible decision-making criterions is finally concluded by analysis and studies，which is bearing to command on position firing.

anti-tank missile，vision intersection，mathematical model，decision-making criterion

TP391.9

A

1002-0640（2015）03-0134-03

2014-01-26

2014-03-21

军队重点基金资助项目（2011XSZZ-009）

魏现杰（1976- ），男，河北元氏人，硕士，讲师。研究方向：武器系统与运用工程。