空间载波数字散斑干涉光路关键参数研究

刘 凯 吴思进 高新亚 祝连庆 杨连祥

(北京信息科技大学仪器科学与光电工程学院1，北京 100192；合肥工业大学仪器科学与光电工程学院2，安徽 合肥 230009；奥克兰大学机械工程系3，美国 密西根州罗彻斯特 48309)

空间载波数字散斑干涉光路关键参数研究

刘 凯1吴思进1高新亚2祝连庆1杨连祥3

(北京信息科技大学仪器科学与光电工程学院1，北京 100192；合肥工业大学仪器科学与光电工程学院2，安徽 合肥 230009；奥克兰大学机械工程系3，美国 密西根州罗彻斯特 48309)

近年来，在数字散斑干涉技术(DSPI)中应用空间载波技术来获取干涉相位，克服了传统DSPI只能用于静态测量的缺点，提高了DSPI的测量速度，实现了动态测量。基于空间载波技术的DSPI测量理论已有相应的研究，但其光路参数的确定和优化还有待进一步的研究。通过分析空间载波数字散斑干涉技术的测量原理，对空间载波数字散斑干涉光路中的关键参数(如光阑孔径、参考光入射角度)进行了理论分析和试验验证，并给出了各自的选择依据。

数字散斑干涉 空间载波技术 傅里叶变换 形变测量

0 引言

数字散斑干涉技术(digital speckle pattern interferometry,DSPI)是一种全场、非接触、高精度的光学测量方法，已被广泛应用于精密机械制造、材料科学及生物医学等领域[1-4]。DSPI根据所测的相位值和光路几何关系来计算物体的形变量[5]，其中，相位的测量是DSPI的关键技术。时间相移技术由于具有高精度、易实现等特点，被广泛应用于DSPI的相位测量[6]，但由于其执行过程的局限性而不能用于动态形变的测量[7]。在工程中，对于由温度变化引起的物体外形蠕变，或者由冲击、爆炸等引起的物体形状瞬变等动态形变的测量具有更加重要的意义。近年来，人们在DSPI中引入了空间相移技术[8-9]和空间载波技术[10-11]，无需利用多幅不同时刻的散斑干涉图进行相位计算，克服了时间相移技术的局限性，实现了DSPI技术对物体动态形变的测量。空间载波技术与空间相移技术相比，其光路更简单，处理更方便，实用性更强，在快速准确地获取干涉相位信息方面展现出了巨大潜力[12]。

本文通过理论分析和试验研究，对影响频谱分布的DSPI光路参数进行分析，主要研究光阑的孔径尺寸和参考光的入射角度等关键参数对频谱分布的影响。

1 空间载波数字散斑干涉的测量理论

DSPI基于散斑干涉原理，通过测量被测物形变前后散斑场的变化，获得散斑中包含的相位信息，从而得到物体的形变大小。图1是一种典型的空间载波数字散斑干涉离面形变测量的光路结构。

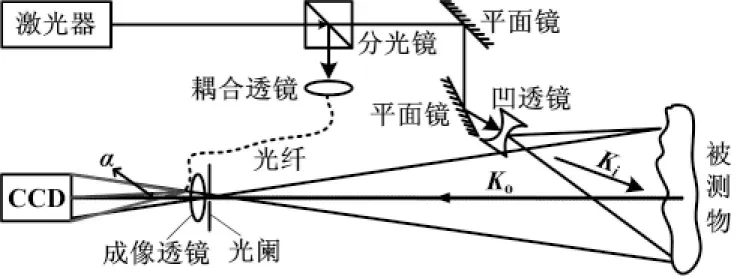
图1 空间载波数字散斑干涉离面形变测量光路

在图1所示光路中，从激光器射出的激光被分光镜分为物光和参考光，物光经过凹透镜扩束后照射到被测物的表面，其漫反射光通过光阑和成像透镜照射到CCD上。参考光通过耦合透镜耦合进入光纤，并相对物光光轴以一定的角度照射到CCD上，形成空间载波。物光和参考光在CCD表面产生干涉，通过CCD即可记录数字散斑干涉图并保存至计算机，进行进一步的处理和运算。

散斑干涉图的强度分布可以表示为：

I=[u(x,y)+r(x,y)][u(x,y)+r(x.y)]*=

对上式进行傅里叶变换，可得：

F(I)=U2+R2+U(fx,fy)⊗R(f0x,f0y)*+

U(fx,fy)*⊗R(f0x,f0y)

(1)

式中：F表示傅里叶变换；⊗表示卷积；U=F(u)；R=F(r)，低频项U2+R2主要包含背景光信息，互为共轭的高频项U(fx,fy)⊗R(f0x,f0y)*和U(fx,fy)*⊗R(f0x,f0y)包含干涉相位信息。通过引入载波，使空间频谱中包含干涉相位信息的项发生频移，从而与包含背景光信息的项分离开来，因此可以通过频率滤波，滤除低频项，只保留包含干涉相位信息的高频项。对滤波后的频谱进行傅里叶逆变换后，可利用下式求得相位分布：

(2)

利用相同的方法分别求解物体形变前后的相位分布，然后得到两者之间的相位差Δ，最后根据光路几何关系求解物体的形变。对应图1所示的光路，相位差Δ与离面形变w之间的关系可表示为：

(3)

式中:φ和φ′为物体形变前后的相位分布；λ为激光波长；α为物光照射角。

2 参数分析及实验验证

2.1 光阑孔径

在光学系统中，孔径光阑起到限制光束口径的作用，在频域则体现为限制了光的空间频率。光阑作用如图2所示，光阑孔径直径为a，光阑与CCD的距离为d，A为干涉图的零级条纹，B为一级条纹，A、B间的距离为L，则物光的空间频率表示为：

(4)

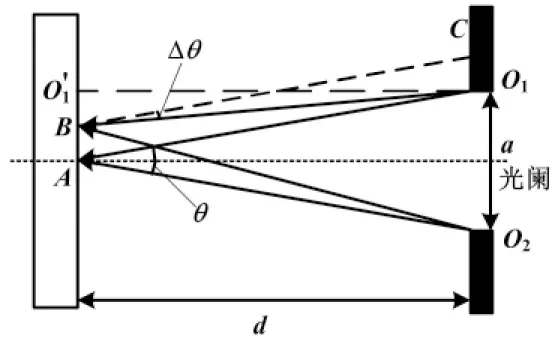
图2 光阑作用示意图

在一级条纹处，物光和参考光光程相差一个波长，即：

(5)

由式(4)和式(5)可得：

(6)

假定物光最高空间频率为fM，则低频项的最大空间频率为2fM，包含干涉相位信息的频谱部分的空间频率范围为2fM。为使频谱有效分离，需满足目标频谱的最高空间频率≥4fM。在满足奈奎斯特采样定理的条件下，有：

(7)

式中：fp为CCD的采样频率。综合式(6)和式(7)，有:

(8)

而：

(9)

因此，光阑直径应满足:

(10)

根据上述原理，试验中采用波长532nm激光器，光阑距CCD160mm，CCD采样频率为2.2×105Hz，求得光阑直径a≤2.34mm。将光阑直径分别调节至1mm、1.5mm、2mm、2.5mm，观察其频谱图，如图3所示。

图3 光阑孔径对频谱的影响

从图3的(a)、(b)、(c)图可以看出，当光阑孔径a≤2.34mm时，频谱能够有效地被分离，而图3(d)所示光阑孔径a=2.5mm时，频谱中包含背景光信息的部分与包含干涉条纹信息的部分发生了重叠。试验表明：光阑孔径越小时越利于频谱分离，而且光阑孔径大小仅决定频谱中各部分的面积，而不影响各部分的中心位置。但是从试验中也可知，较小的光阑孔径尺寸会降低光能的利用率，增加对激光器输出功率的要求。

空间载波数字散斑干涉技术的主要优点在于能够测量动态形变，但是相比于传统数字散斑干涉技术，其成像光阑孔径较小、光能损失率高，因此对激光器的输出功率有更高的要求。尤其在测量高速动态形变时，要求相机工作在较高帧率，对应的拍照曝光时间也更短，此时对激光器输出功率有更高的要求。因此，光阑孔径过大会影响频谱图的质量，严重时将导致测量无法进行；光阑孔径过小会导致有效光能量较低，使得系统无法应用于高速动态形变的测量。理想的光阑孔径尺寸应兼顾测量质量和测量速度的要求，在保证能够有效分离频谱，即满足式(10)描述的限制条件的前提下，尽量稍大一些，以增加透光量，使空间载波数字散斑干涉技术能够满足动态形变测量的要求。

2.2 参考光的入射角度

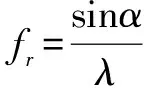
(11)

在满足奈奎斯特采样定理的条件下，又有:

(12)

综合式(11)、式(12)后，得到：

(13)

试验中通过调整参考光入射点的位置，改变参考光入射角度。设参考光入射点相对光阑中心的偏移量为l=dtanα，则：

为验证该结论，在2.1节实验的基础上选用1.5mm的光阑，根据上式计算出l的取值范围为4.1 mm≤l≤8 mm。为方便调节参考光入射点，首先使参考光入射点与光阑中心重合，然后使其在光阑平面内沿同一方向移动，分别记录偏移量为0、2、4、6、8、10 (单位:mm)时的散斑图，通过傅里叶变换得到相应的频谱，如图4所示。

图4 参考光入射角对频谱的影响

从图4可以看出，当l=0 mm、2 mm时，频谱无法有效分离;当l=4mm时,频谱大致分离但有一小部分重叠;当l=6mm、8mm时，频谱分离较好;当l为10mm时高频部分则超出边界而不完整。试验结果表明，参考光的入射角度决定了频谱中包含干涉相位信息的部分的位置。为实现频谱有效分离，应使参考光的入射角满足式(13)的限制条件。

3 结束语

本文推导了光阑孔径和参考光的入射角满足试验条件的取值范围，并通过试验对所推导结果进行了验证，证明所得结果的正确性。由试验得出结论：光阑孔径决定频谱中各部分面积的大小，参考光的入射角度决定频谱中各部分的位置，为使频谱有效分离，试验中应选择合适的参考光入射角和较小的光阑孔径。但光阑过小也会导致物光频谱较窄，能量较小，对光源利用率低，同时又使散斑图信噪比降低，因此在实际试验过程中选择合理的光阑孔径也至关重要。

[1] Yang L X,Zhang P,Liu S,et al.Measurement of strain distributions in mouse femora with 3D-digital speckle pattern interferometry[J].Optics and Lasers in Engineering, 2007,45(8):843-851.

[2] Solís S M,Hernández-Montes M,Santoyo F M.Measurement of Young’s modulus in an elastic material using 3D digital holographic interferometry[J].Applied Optics,2011,50(20):3383-3388.

[3] Shakher C,Kumar R.Application of digital speckle pattern interferometry(DSPI) in determination of elastic modulus using plate vibration[J].Recent Advances in Mechanics,2011(11):329-341.

[4] Campos L,Parra D F,Vasconcelos M R,et al.DH and ESPI laser interferometry applied to the restoration shrinkage assessment[J].Radiation Physics and Chemistry, 2014(94):190-193.

[5] Wu S J,Zhu L Q,Feng Q B,et al,Digital shearography with in situ

phase shift calibration[J].Optics and Lasers in Engineering,2012,50(9):1260-1266.

[6] Yang L X,Xie X,Zhu L Q,et al.Review of electronic speckle pattern interferometry(ESPI) for three dimensional displacement measurement[J].Chinese Journal of Mechanical Engineering,2014,27(1):1-13.

[7] Zhu L Q,Wang Y H,Xu N,et al.Real-time monitoring of phase maps of digital shearography[J].Optical Engineering,2013,52(10):15-19.

[8] Bhaduri B,Mohan N K,Kothiya l.Use of spatial phase shifting technique in digital speckle pattern interferometry(DSPI) and digital shearography(DS)[J].Optics Express,2006,14(26):11598-11607.

[9] Bhaduri B,Kothiya l,Mohan N K.Curvature measurement using three-aperture digital shearography and fast Fourier transform[J].Optics and Lasers in Engineering,2007(45):1001-1004.

[10]Khaleghi M,Lu W,Dobrev I,et al.Digital holographic measurements of shape and three-dimensional sound-induced displacements of tympanic membrane[J].Optical Engineering,2013,52(10):101916.

[11]Pedrini G,Osten W,Gusev M E.High-speed digital holographic interferometry for vibration measurement[J].Applied Optics,2006,45(15):3456-3462.

[12]Gao X Y,Wu S J,Yang L X.Dynamic measurement of deformation using Fourier transform digital holographic interferometry[C]//Proceeding of SPIE 8916:Sixth International Symposium on Precision Mechanical Measurements,Guiyang,China,SPIE,2013.

Research on the Key Parameters of Optical Path for Spatial-carrier Digital Speckle Pattern Interference

In recent years, the spatial carrier technology has been applied in digital speckle pattern interferometry (DSPI) to obtain interferometric phase, thus the disadvantage of traditional DSPI that is only used for static measurement is overcome, and the measurement speed of DSPI is increased for implementing dynamic measurement. The measurement theory of the DSPI based on spatial carrier technology has been researched, but the determination and optimization of the parameters of optical path need to be studied in further. Through analyzing the measurement principle of spatial carrier DSPI, theoretical analysis and experimental verification for the critical parameters of optical path, such as aperture size and incidence angle of reference beam are conducted, and the basis of selection is given respectively.

Digital speckle pattern interference Spatial-carrier technique Fourier transform Deformation measurement

国家自然科学基金资助项目(编号：51275054)；

北京市自然科学基金资助项目(编号：3144028)。

刘凯(1988-)，男，现为北京信息科技大学光学工程专业在读硕士研究生；主要从事全场光测试技术方面的研究。

TH74

A

10.16086/j.cnki.issn1000-0380.201509009

修改稿收到日期：2015-12-04。