融合多物理信息的超声波测量系统研究

任思源 刘 石 宋 灿 闫 勇

(华北电力大学能源动力与机械工程学院1，北京 102206；华北电力大学控制与计算机学院2，北京 102206)

融合多物理信息的超声波测量系统研究

任思源1刘 石2宋 灿2闫 勇2

(华北电力大学能源动力与机械工程学院1，北京 102206；华北电力大学控制与计算机学院2，北京 102206)

对于工业工程中的距离与温度测量，非侵入、无干扰式测量方法日显重要。为此，利用超声波飞渡时间与相位差两种非侵入方法，对距离与温度的同时测量进行了研究。采用单片机作为核心，结合外围电路，构建了超声波测量系统硬件，并用Monte Carlo方法对硬件系统进行了仿真与误差分析。实验结果显示，该系统的测量相对误差不超过3%，为Monte Carlo方法的工业应用奠定了基础。

超声波 单片机 温度测量 距离测量 Monte Carlo方法

0 引言

在工业测量中，距离与温度是人们广泛关注的两个物理量。距离测量是多种机械应用与控制应用的依据，如物位测量、机器人视觉识别、管道尺寸、汽车防撞等[1]。同样地，温度测量对于大型锅炉的在线监测、优化燃烧、降低污染以及保障设备安全运行都具有极其重要的意义[2]。

超声波测量技术是一种典型的非接触式测量方法，它通过超声波的产生、在介质中传播及接收回波的物理过程来实现[3]。由于超声波为机械波，对外界光线和电磁场不敏感，因此可用于黑暗、有灰尘或烟雾、电磁干扰强等恶劣环境中。同时，超声波传感器价格低廉、安装简单，特别适用于发电厂、变电站等电磁干扰强的电力工业测量中。

基于超声波测量的诸多优点，同时为满足电力工业中对距离与温度测量的需要，本文提出一种超声波距离、温度综合测量系统。该系统能应用于多种电力工业的多种测量场合，可满足多种应用需求。

1 测量方法

应用超声波进行测量主要采用两种方法：飞渡时间法[4]与相位差测量法[5]。这两种方法均可测量距离与温度。

1.1 飞渡时间法

飞渡时间法是通过硬件测量出超声传感器发射端至接收端的飞行时间，如果要测量距离，则需确定测量时的温度。根据热力学中气体状态方程和声波运动方程，推导出超声波在气体中的传播速度c和气体的温度T之间的关系，从而确定环境声速，如式(1)所示[6-8]。

(1)

式中：c为声速；Z为气体组成决定的常数，对空气而言，其值为20.045[9]。

由运动学公式得出测量距离，如式(2)所示。

L=ct

(2)

式中：L为测量区域距离；t为飞渡时间。

由于待测区域尺寸规格已知，则由式(3)可得出声速。

c=L/t

(3)

由式(1)、式(3)可得出测量温度，如式(4)所示。

T=(L/Zt)2

(4)

由上述分析可知，无论是测量距离，还是测量温度，得到准确的飞渡时间是测量的关键。

1.2 相位差测量法

假设超声发射端与超声接收端的距离为L，超声波波长为λ，超声波信号频率为f，整波长数即完整周期数为N，不完整波长即测量相位设为φ，则有：

L=(N+φ)λ

(5)

又由声速c与波长频率的关系可得出：

L=(N+φ)c/f

(6)

根据超声传感器的最佳性能区间，选取2个不同的频率f1、f2，则由式(7)表示不同频率时的测量结果：

(7)

通过选取相近的频率，可将相位差调整在一个周期之内，即N1=N2，则由式(7)可推出[10]：

LΔf=cΔφ

(8)

式中：Δf=f2-f1；Δφ=φ2-φ1。在温度稳定的测量条件下，根据式(1)与式(8)，可最终确定距离测量值，如式(9)所示。

(9)

如果距离已知，需要测量温度，则由式(1)与式(8)最终测定温度，如式(10)所示。

(10)

针对距离测量，由于Δφ存在误差叠加问题，因此本文系统采用单频率相位差法进行距离测量，即N1=N2=0。

2 硬件系统

根据上述测量原理与方法，本文提出一种融合距离、温度、温度分布多物理信息的超声波综合测量系统。该系统以单片机作为核心，外围电路包括发射信号放大电路、超声波换能器选择电路、超声波发射和接收电路、接收信号滤波整形电路、相位比较电路和接收信号反馈电路等。该系统采用STC12单片机作为核心器件，由其产生超声波换能器的使能信号，控制超声波换能器选择电路、处理滤波整形后的接收反馈信号并实现与上位机通信传输数据。超声换能器具备发射与接收超声波两种功能，这两种功能的选择分工由单片机与多路开关共同组成的控制电路来完成。超声波接收端的滤波整形电路必不可少，这是因为超声波属于机械波，在空气中的损耗相当大，接收到的信号衰减严重，而且随着距离的增加，衰减呈比例增加。如果不加入滤波整形，几乎很难消除噪声的影响，将直接导致测量失准。本系统采用前端放大结合施密特触发器实现滤波整流。利用触发器选定电压阈值法，确定发射波与接收波的起始时刻完成时间差测量；利用相位比较芯片实现相位差测量。超声波测量系统框图如图1所示。

图1 超声波测量系统框图

系统测量时，首先由功能选择开关选择进行距离测量或温度测量。距离测量包括相位差法和飞渡时间法两种测量方法，因此由多路开关选择其中一种测量方法进行距离测量。温度测量包含单组温度测量和温度分布测量两种测量方式。单组温度测量只需要一对超声波换能器即可进行; 温度分布测量则需要多个超声换能器环绕被测空间截面，由单片机控制多个换能器进行多路测量，并将多组测量信息返回至上位机，由成像算法进行温度分布图像重建。

3 误差分析

对于距离与温度的测量，无论采用飞渡时间法还是相位差法，都需要明确测量中存在的主要误差。在实际测量时，如果不考虑人为误差，主要的客观误差分为电气误差和环境误差两类。

① 电气误差，主要由选取的硬件及测量电路造成。针对本测量系统，主要分为超声波换能器的电气误差与测量电路的电气误差。

② 环境误差，主要由测量时的风速与湿度引起，测量距离时温度也是环境误差之一。其中电气误差中超声换能器带来的误差不容忽视。由于系统采用压电式超声换能器，其工作原理是利用压电材料的压电效应进行能量转换，因此，在超声波测量时发射与接收时均存在电气误差。设发射信号为[11]：

Ae(t)=Asin(ωt+φ0)

(11)

式中：φ0为发射信号初始相位；Ae为发射信号；A为发射信号幅值；ω为发射信号角频率。

ω=2πf

(12)

经过测量区域后，接收信号为[9]：

(13)

式中：Ar(t)为接收波信号；Ar为接收波幅值；L为测量区域距离；c为声速；φc为信号经过电路引起的电气误差。由式(14)得出测量时间误差。

(14)

式中：TE为时间误差；T为超声波一个周期的时间。

由此可见，电气误差的大小在一定程度上决定着测量结果的精确度。此外，风速和湿度等环境因素带来的测量误差也是不容忽视的。需要特别指出的是，在测量距离时，温度影响被认为是一种误差来源，而在测量温度时，正是利用了温度不同引起的声速的变化来进行温度测量。为了验证测量的准确性，在充分考虑上述误差来源的情况下，本文首先采用MonteCarlo方法进行仿真，在验证测量的准确性后再进行选择器件及实际测量。

MonteCarlo方法的基本思想是：将某个事件的概率，通过某种实验的方法得出该事件发生的频率，再通过频率得到问题的解。MonteCarlo方法的关键步骤在于随机数的产生，因为影响事件的因素有时是不可预测的，比如温度测量中随时变化的风速、湿度等环境因素。因此，由计算机产生一组符合事件发生概率的伪随机数，也可以近似地将其作为真实的随机数使用。应用高斯分布函数产生伪随机数，近似模拟风速、湿度变化引起的环境误差发生概率，基本符合实际应用情况下的数学统计规律。

根据上述硬件结构，在仿真中加入超声测量系统的各部分误差：

① 放大器芯片产生的白噪声范围，电气误差；

② 超声波换能器的电气误差；

③ 湿度、风速等不确定的环境误差。

在考虑上述所有误差的情况下，分别以飞渡时间法与相位差法在相同温度下进行模拟，当超声波在空气中传播时，超声传感器之间距离固定为20cm，温度为20 ℃时，声速约为326.68m/s。取1 000组随机样本，按照电气误差引起的不同测量结果进行仿真，结果如图2所示。

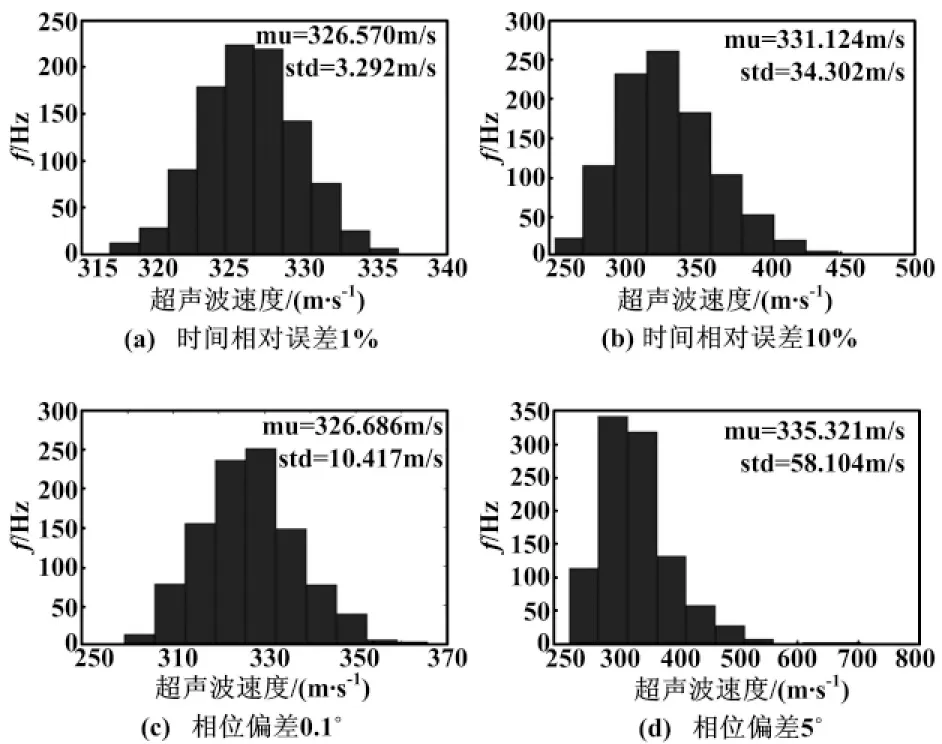
图2 超声波速度测量仿真图

图2中，mu为数学期望，std为方差。从图2可以明显看出，在环境误差存在的情况下，超声波换能器及测量电路带来的电气误差将对测量结果产生不容忽视的影响。从图2(a)和图2(b)可以看出，当利用飞渡时间法进行测量时，由超声换能器及测量电路造成的电气误差对时间测量相对误差在1%时(即本仿真样本情况中时间偏差为6.12 μs时)，速度测量误差不足1%；而当时间测量相对误差达到10%时(即本样本中时间偏差为61.2 μs时)，本系统声速测量出现明显偏差，误差将超过10%。由图2(c)和图2(d)得出，当存在5°的偏差时，声速的测量结果产生严重偏差(在采用相位差方法测量时，需要采用相移电路来消除电气误差[10-11])。超声波相位差法测量过程中，由于需要调整两个不同频率的完整周期相等，因此，在测量时本身就带有局限性。而最重要的是，对于两个频率的单频测量值φ1与φ2所存在的误差，最终转化为Δφ，会造成误差叠加，对测量的准确度有很大影响。因此，相位差测量方法对超声波换能器的电气误差要求非常严格。

4 系统测量实验

4.1 距离测量实验

通过上述误差分析，明确了测量中对测量结果的影响因素。因此，在距离测量实验过程中，为了减小环境因素对测量结果的影响，采用防风罩减小外界环境风速的影响，通过温度计监测实验过程的温度，基本稳定在28.6 ℃。除此之外，通过热线风速仪监测防风罩内空气流动状况。在完成实验准备工作后，利用电动平移台，进行精确距离测量，设定电动平移台步进0.08 mm，测量距离为0～51.2 mm，采用40 kHz作为超声波发射波频率，100 mm作为预热波传播距离(在此距离下完全消除了盲区的影响)。测量中采用的相位差比较芯片为超声波相位差法距离测量系统的核心器件。在实际测量时，相位差比较芯片工作基本正常，但由于实际测量时环境的影响与电气误差的存在，芯片输出电压与理想值存在波动，符合仿真结果。通过相位差比较芯片的输出电压与相位差之间的关系计算得出，实际测量时芯片相位差信息与理论值偏差应在30°以内，最大偏差60°左右；距离测量结果的相对误差应在3%左右，最大相对误差不超过6%。实际测量值如图3所示。

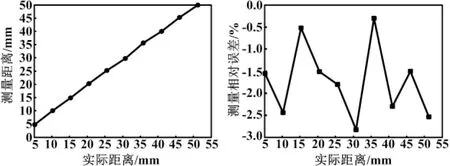
图3 超声波距离测量图

4.2 温度测量实验

针对温度测量，选取两个超声换能器在恒温箱内进行测量，其中一个作为发射器，另一个作为接收器。发射器与接收器正面相对放置，且两者之间的距离为25 cm。逐步改变恒温箱内的温度，以热电偶测量温度为基准算出参考时间，验证本超声波温度测量系统的测量精度。根据热电偶测得参考温度反推出该温度下的声速，由式(1)可得出参考时间，与实际测量时间的对比如图4所示。

图4 时间测量对比图

超声波温度测量如图5所示。

图5 超声波温度测量图

由图5可看出，热电偶测量值与超声波测量值密切相关，且在测量范围内，超声波测量值与热电偶参考值的相对偏差不超过3%。

5 结束语

为满足工业测量中对距离与温度测量的需要，提出了一种超声波距离、温度综合测量系统。该系统可应用于多种工业测量场合，如物位测量、管道尺寸测量、大型锅炉的在线监测、优化燃烧等。同时，由于超声波为机械波，对外界光线和电磁场不敏感，可用于黑暗、有灰尘或烟雾、电磁干扰强等恶劣环境中，特别适合用于发电厂、变电站等电磁干扰强的电力工业测量环境。系统可分别采用超声波飞渡时间法与相位差法，实现对距离尺寸及温度的测量。针对系统的硬件设计，基于Monte Carlo方法进行了模拟仿真与误差分析，得出了系统测量的误差范围，并进行了距离与温度的测量试验。试验表明，该系统针对距离测量相对误差在3%以内，温度测量的相对偏差不超过3%。

[1] 苑洁.基于STM32单片机的高精度超声波测距系统的设计[D].北京:华北电力大学,2012.

[2] 邵岩声学法温度场图像重建的研究[D].沈阳:东北大学,2008.

[3] 常太华,苏杰,田亮.检测技术与应用[M].北京:中国电力出版社,2003.

[4] 刘岩,Hermann I S,刘石.基于窄带宽超声传感器的传播时间测量方法[J].自动化仪表,2014(4):72-78.

[5] Ren S Y,Liu S.Temperature detection circuit system research based on ultrasonic phase difference method[J].Applied Mechanics and Materials，2013(411):1625-1630.

[6] 颜华,崔柯鑫,续颖.基于少量声波飞行时间数据的温度场重建[J].仪器仪表学报,2010,31(2):470-475.

[7] Bramanti M,Salerno E A,Tonazzini A,et al.An acoustic pyrometer system for tomographic thermal imaging in power plant boilers[J].IEEE Transactions on Instrumentation and Measurement,1996,45(1):159-167.

[8] Tsai W Y,Huang C F,Liao T L.New implementation of high-precision and instant-response air thermometer by ultrasonic sensors[J].Sensors and Actuators A,2005(117):88-94.

[9] 颜华,陈冠男,杨奇,等.声学CT复杂温度场重建研究[J].声学学报,2012,37(4):370-377.

[10]Huang S S,Huang C F,Huang K N,Young M S.A high accuracy ultrasonic distance measurement system using binary frequency shift-keyed signal and phase detection[J].Review of Scientific Instruments,2002,73(10):3671-3677.

[11]沈常宇,郭宝金.相位比较法高精度超声测距研究[J].传感技术学报,2010,23(6):893-895.

Research on the Ultrasonic Measurement System Integrating Multiple of Physical Information

In distance and temperature measurement for industrial processes, the non-invasive and non-interference measuring method becomes increasingly important. Therefore, the simultaneous measurement of both distance and temperature by adopting two of the non-invasive methods, i.e., ultrasonic flying time and phase difference methods is researched. With the single chip machine as the core, and combining with peripheral circuits, the hardware of the ultrasonic measurement system is constructed; and the simulation and error analysis for hardware are accomplished by using Monte Carlo method. The experimental results indicate the relative measurement error does not exceed 3%, this laid the foundation of industrial applications for this method.

Ultrasonic wave Single chip computer Temperature measurement Distance measurement Monte Carlo method

教育部高等学校学科创新引智计划基金资助项目(编号：B13009)；

中央高校基本科研业务费专项资金资助项目(编号：JB2014200)。

任思源(1982-)，男，现为华北电力大学工程热物理专业在读博士研究生；主要研究方向为超声波检测技术。

TH89

A

10.16086/j.cnki.issn1000-0380.201509007

修改稿收到日期：2015-01-06。