转向制动工况的多轴轮式装甲车辆模型与试验验证*

徐国英，王 闯，姚新民，王 睿

(装甲兵工程学院机械工程系，北京 100072)

0 引言

目前车辆动力学仿真建模的方法主要三种:人工建模、计算机建模和图形建模［1］。各种精度的车辆动力学模型适用于不同的研究方向与内容。本文在进行车辆行驶稳定性仿真的过程中，既需要对车辆的行驶状态进行仿真，又需要植入所设计的控制器进行控制用来提高其稳定性［2－3］。Matlab/Simulink中包含的功能齐全的各类模块可以方便地进行车辆系统动力学的建模，同时也较容易接入控制器，因此比较适合进行车辆动力学稳定性控制系统的仿真研究。

1 多轴轮式装甲车动力学模型

1.1 轮胎模型

轮胎模型可以分为理论模型、经验模型和半经验模型［4］。本文采用的理论模型中的UA模型实现车轮动力学仿真。UA模型是国内使用较多的理论模型，建模过程中将车轮简化成为一系列三维弹簧，根据弹簧变形和轮胎与路面纵向、侧向和纵向力之间的关系，建立轮胎与路面之间接触的动态方程，通过解方程可以得到轮胎纵向力和侧向力［5］。

1.1.1 车轮滑动率

制动工况中，车轮沿xw轴和yw轴的滑转率为:

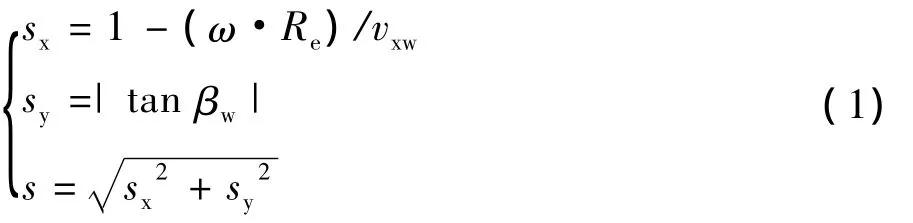
式中:vxw为车轮中心沿xw轴向速度;ω为车轮转动角速度;Re为车轮有效半径;βw为车轮侧偏角。

1.1.2 地面附着系数

UA轮胎模型假设路面附着系数随着滑移率发生线性变化:

式中:μ0为地面最大附着系数;μ1为车轮纯滑动时的地面附着系数。

地面间沿着xw轴的附着系数和沿着yw轴的附着系数分别为:

轮胎在不同车辆行驶状态下会产生滑动与滚动两种状态，可求得轮胎滚动与滑移临界点的临界纵向滑移率为:

式中:Fz为轮胎所受垂直载荷;Kx为纵滑刚度。

临界侧向滑移率为:

式中:Ky为轮胎侧偏刚度。

由此可定义无量纲滑移率:该车制动器为蹄鼓式制动器。制动器制动效能因数表示为:

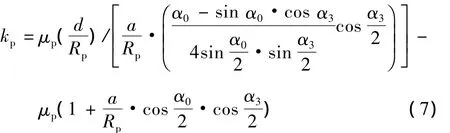
式中:μp为摩擦片摩擦系数。制动传动机构将高压气体输送到制动气室内，制动气室产生的制动力矩可以计算为:

式中:ij为表示车辆左前轮fl，右前轮fr，左中轮ml，右中轮 mr，左后轮 rl，右后轮 rr，下同;pij为制动器制动气室内压力值;Apij为相应的制动气室有效面积;ηpij为传动机构机械效率;kpij为制动器制动效能因数;lpij为调整臂有效长度;rij为制动凸轮基圆半径;Rij为制动鼓半径。

1.2 整车模型

该模型考虑整车纵向、侧向、侧倾和横摆运动，车轮转动，忽略空气阻力对整车的影响。

图1 三轴轮式车辆整车模型

该三轴装甲车辆整车受力分析如图1所示，可以得到车辆动力学方程:

(1)沿x轴纵向运动方程:

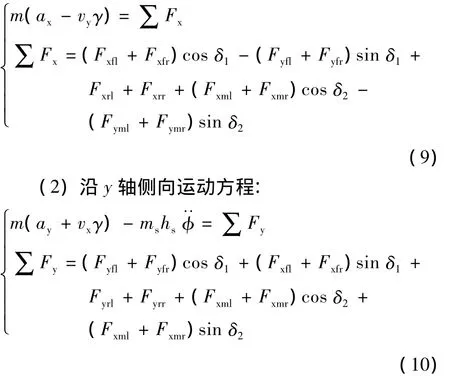
式中:Fy表示整车所受侧向力合力。

(3)绕z轴横摆运动方程:

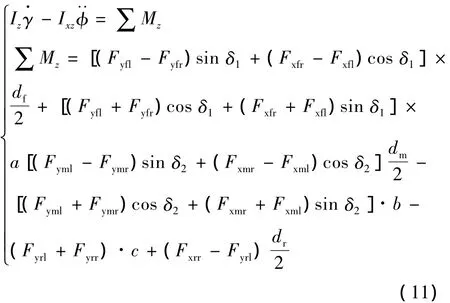
式中:Mz为整车绕 z轴所受的力矩;Iz、Ixz分别为整车绕z轴的横摆转动惯量和绕x、z轴的转动惯量积。

(4)绕x轴侧倾运动方程:

式中:Kφ、Cφ分别表示侧倾运动等效刚度和等效阻尼系数。

(5)车轮滚动方程:

式中:Iw为车轮的转动惯量;Tbij为对应车轮所受的制动力矩;Tfij为对应车轮滚动阻力矩;f为轮胎在道路上的滚动阻力系数，根据经验可由下式估算:

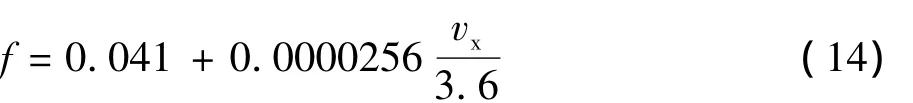
2 车辆动力学模型在Matlab/Simulink中的搭建

模型中各部分关系如图2所示，整体建模如图3所示，各参数相互作为输入输出，进而形成一个闭环系统。

仿真前，车辆所有的结构参数和初始条件通过M文件的形式进行设定;工况选择模块用于工况的设定，驾驶员指令模块用于实现对车辆转向制动的控制，通过状态观察器实现对车辆状态的观测。

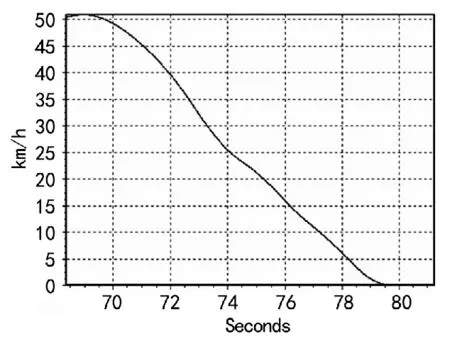
图2 50 k m/h制动试验数据

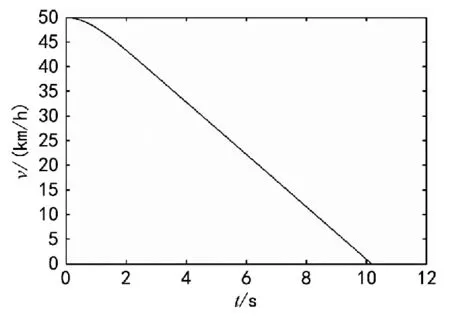
图3 30 km/h制动横摆角速度响应试验数据与仿真数据

3 车辆制动器模型和阶跃响应的试验验证

(1)基于一种曲柄滑块式转向传动机构进行理论分析，并利用MATLAB进行设计计算，确定目标函数、设计变量和约束条件，对该机构进行优化设计。结果表明，由该机构所决定的转向曲线与理论阿克曼曲线基本一致，验证了所建立的数学模型的可靠性。为保证该模型在转向制动工况下仿真的准确性，需要验证其能否可以为行驶稳定性控制器的设计及仿真验证打下基础。

直线制动试验中，车辆沿平直跑道行驶，车速分别达到20、40、50 km/h时踏死制动踏板，直至车辆停止，测量车速与制动时间。其目的在于验证动力学模型中制动系统的准确性，得到制动时车辆行驶参数可修正模型中制动系统的设定。

以50 km/h速度下的直线制动为例，见图4所示。通过速度单位换算，可以得到实车试验所测得的制动时间与仿真实验所得到的制动时间基本一致，偏差不大，说明本章所建立的车辆动力学模型中的制动器模型可以达到精准度要求。

图4 50 km/h制动仿真数据

角阶跃制动试验中，车辆沿平直跑道行驶，达到指定车速15、30、40 km/h后，将车辆转向盘向右迅速转动90°后保持并踩制动踏板到底直至停止，记录横摆角速度响应值。

以30 km/h速度下的试验与仿真数据为例，根据方向盘转角与前轮转角的传动比，方向盘转角为90°时，车轮转角约为2°，经过角度与弧度的换算关系可以看出，各车速下仿真数据与试验数据拟合较好。

通过直线制动试验与角阶跃制动试验，验证了模型中制动器数学关系的正确性和横摆响应的准确性。

4 总结

针对所研究的三轴轮式装甲车辆的特点和转向制动工况的需求建立了简化且符合要求的车辆系统模型，在Matlab/Simulink软件中完成了各模块的搭建工作，并利用实车试验初步验证了其准确性，为之后横摆力矩控制算法的研究、验证提供了仿真平台。

［1］ 房占鹏.汽车操纵稳定性模型及仿真方法研究［D］.重庆:重庆理工大学，2010.

［2］ 张红党，商高高.基于主动前轮转向横摆角速度反馈控制的研究［J］.机械设计与制造，2009(4):203－205.

［3］ 苏周成.车辆转弯制动稳定性动力学控制研究［D］.重庆:重庆大学，2007.

［4］ 饶志明.轻型汽车的电子机械制动与驱动防滑控制系统研究［D］.长春:吉林大学，2009.

［5］ Gim G，Nikracesh P E.An Analytical Model of Pneumatic Types for Vehicle Dynamic Simulations［J］.PartⅠ:Pure Slips，International Journal of Vehicle Design，1990，11(6):1－4.

［6］ 陈 晴.三轴气压制动汽车防抱死与驱动防滑控制系统研究［D］.长春:吉林大学，2009.