直线伺服电动机自抗扰控制系统研究

党超亮，同向前，杨树德

（西安理工大学自动化学院，陕西西安710048）

与其他类型的直线电机相比，直线伺服电机具有高速度、高精度、高效率、响应快速等优势，在现代制造业拥有非常广泛的发展前景［1-2］。然而由于直接直线驱动，省去了中间传动装置，外部扰动力、摩擦力等外部未知扰动会毫无缓冲的直接施加在电机本体上，同时直线电机是一个强耦合、多变量、非线性的系统，采用传统的控制策略很难使得电机控制系统性能获得本质上的提高［3-4］。在控制策略上，目前在包括交流直线电机在内的交流伺服中普遍采用的是矢量控制，在矢量控制的基础上，很多学者为了进一步提高交流伺服系统的性能，提出了许多非线性应用与直线电机控制。自抗扰策略是近年来用在工业控制，尤其是电机控制中的一种新的非线性控制算法，其不依赖于被控对象精确的数学模型，是针对不确定系统有效实用的控制器［5］。文献［6］将自抗扰应用于永磁同步直线电机的速度控制系统，在这篇文献中作者采用一阶速度ADRC 控制，并未考虑到q 轴电流内环控制误差的影响，从而降低了系统速度响应的动静态特性，有一定的局限性；文献［7］中作者针对速度ADRC 控制系统，d轴电流内环采用了ADRC 控制，q 轴电流内环采用的是比例控制，即ADRC+PD 控制，此种设计并不能完全消除dq 轴电流的动态耦合；文献［8］设计了基于线性自抗扰策略的直线电机位置控制系统，在该文章中作者采用线性自抗扰控制，实验表明，该方法与传统的控制方法相比，改善了系统的动态性能和抗干扰能力。

文中结合矢量控制方法，将ADRC用于直线电机控制系统中，针对电流之间的强耦合作用，将系统扰动项作为未知综合扰动，并利用ESO进行观测与补偿，分别设计了dq 电流的解耦控制，针对速度控制系统分别设计采用了串级一阶ADRC，“ADRC+PID”组合算法、二阶ADRC与改进型ADRC（MADRC）进行系统仿真研究，针对位置控制系统分别采用了MADRC与传统ADRC策略进行了仿真分析，仿真结果表明，系统响应速度快、超调小，具有优良的动静态性能。

1 直线电机数学模型

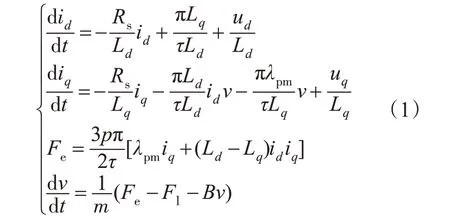
式中：ud，uq分别为d,q轴电压；id，iq分别为d,q轴电流；v为动子运动线速度；Rs为动子相电阻；分别为d,q轴动子电感；λpm为励磁磁链；τ为极距；Fe为电磁推力；Fl为系统阻力；m为动子质量；B为粘滞摩擦系数；p为极对数。

式（1）中主要考虑了负载阻力和粘滞摩擦力扰动，而电机在实际运行过程中还存在其他形式的扰动，如静摩擦、滑动摩擦、风阻、齿槽推力、纹波推力等。将静摩擦力和滑动摩擦力视为一个综合摩擦扰动，其表达式为

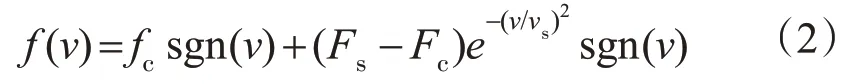
式中：sgn(v)为关于v的函数，其恒为正值；Fc为库仑 摩 擦 力；Fs为 静 摩 擦 力；vs为Steinbeck 效 应系数［9］。

2 自抗扰策略原理

自抗扰控制（auto disturbances rejection control）主要由跟踪微分器（TD），扩张状态观测器（ESO）和非线性误差反馈控制律（NLSEF）3部分组成［10-12］。其原理框图如图1所示。

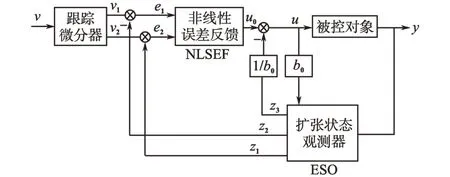
图1 ADRC原理框图Fig.1 The principle block diagram of ADRC

系统实际输出一般都会包含一定的噪声，假如直接利用ESO 测量信号往往难以获得较好的状态变量，依据TD环节的数学描述可知，其频率特性与低通滤波器类似，通带内相移较小且无谐振，为避免跟踪微分过程所带来的相位滞后，通过在传统ADRC 控制中引入了反馈通道来消除测量噪声的不利影响，其结构框图如图2所示。

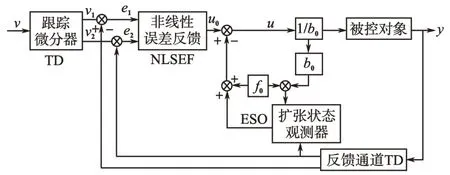
图2 引入反馈通道的ADRC结构框图Fig.2 Block diagram of ADRC with the feedback channel

跟踪微分器（TD）用来减小系统的初始误差，在阻尼不变的情况下，且在被控对象能承受范围内，依据目标信号安排一个合适的过渡过程，从而有效地解决了超调与快速性的矛盾。在此以本文所采用的二阶ADRC 为例，TD 的表达式如下：

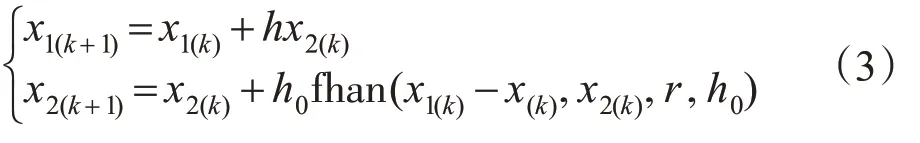
式中：r为参数，决定了系统的跟踪速度，称为速度因子；h为采样周期；h0主要是用来滤除测量噪声，称为滤波因子。

当h取值恒定时，r的取值越大，跟踪微分过程所需的时间越短，当r保持恒定时，h越小跟踪时间相对越短。参数r过大或h过小都容易造成系统波动，在进行系统设计时其值要适当选择。给定参考输入的单位阶跃信号，分别针对上述情况进行了仿真分析，仿真结果如图3、图4所示。

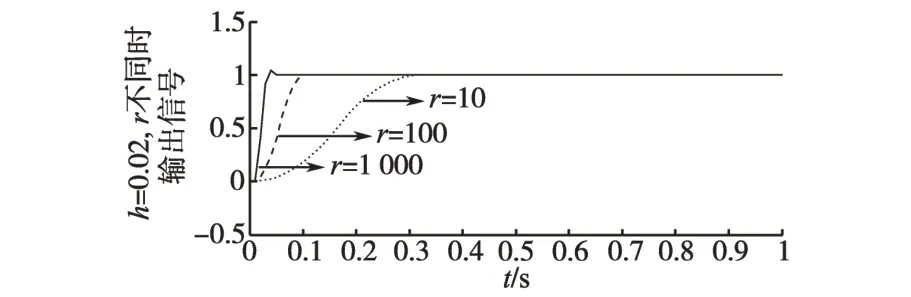
图3 h=0.02，r不同时TD输出波形Fig.3 Waveforms of TD while h is 0.02，r selects different values

图4 r=100，h不同时TD输出波形Fig.4 Waveforms of TD while r is 100，h selects different values

ESO 作为ADRC 的核心部件，主要实现对被控对象的总和扰动的观测和补偿，在采用ADRC 进行系统设计时将施加于被控对象上的外部作用都归结为未知扰动，利用ESO 进行观测和补偿，从而实现动态系统的线性化，ESO 表达式如下：

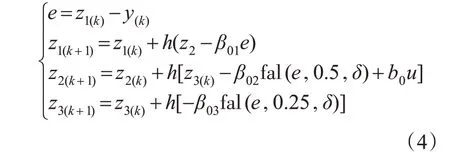
系统状态误差由TD环节输出与ESO估计值所决定，两者所得的误差值输入到NLSEF 运算后，通过与来自ESO 的补偿量取线性加权和，输出系统控制量，NLSEF的表达式如下：

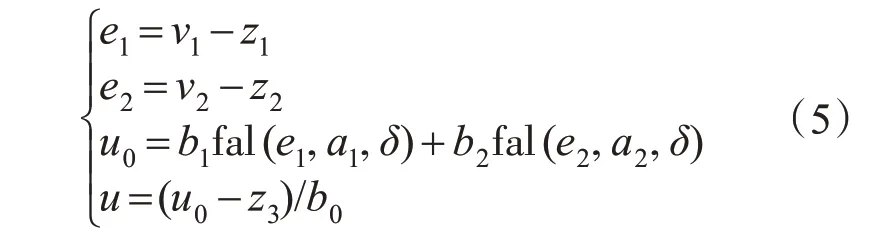
其中幂次函数fal(e,a,δ)方程为

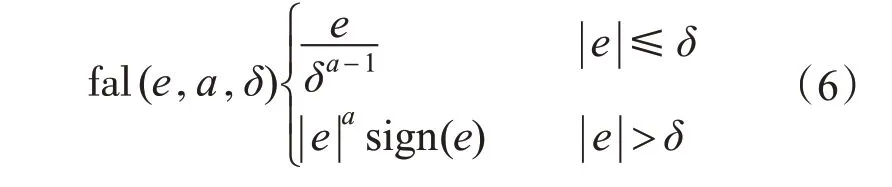
fal(e,a,δ)实现了对控制工程界的先验知识“大误差小增益，小误差大增益”的数学拟合，提高了ADRC的动态性能与鲁棒性。

3 直线电机ADRC控制系统

3.1 dq轴电流解耦控制

从数学状态方程可以看出，直线伺服电机是一个多变量、强耦合的非线性系统，耦合项的存在将会明显地降低控制系统性能，单独控制ud，uq从而实现dq 轴电流控制都会引起环路中所存在的多变量间的耦合作用直接影响到电流控制效果，带来系统超调和调节时间过长等不利影响。

3.1.1 d轴电流解耦控制

为使得电流推力最大化，电流内环采用ADRC控制，其中d轴电流给定为id=0，由于电流给定值为0，为简化系统参数，电流内环控制可以去掉TD环节。

根据式（1），可得离散域内ADRC 解耦控制算法表达式为

ESO：

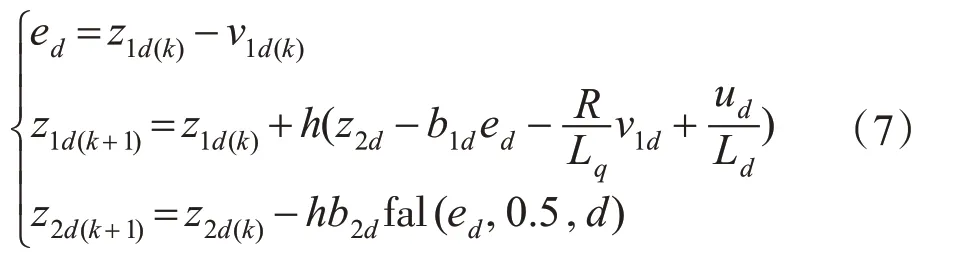
NLSEF：

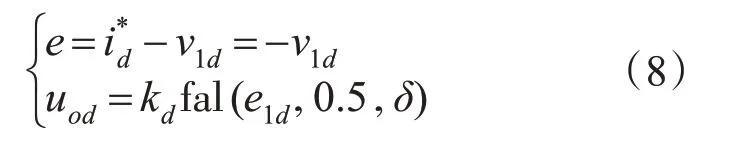
扰动补偿

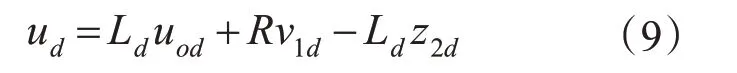
上式中b1d，b2d，δ为待选参数。只要选择合适的参数，ADRC就能利用ESO实现对dq电流之间耦合项的准确观测，即：

3.1.2 q轴电流解耦控制

同理可得，iq的ADRC解耦控制算法表示为

ESO：

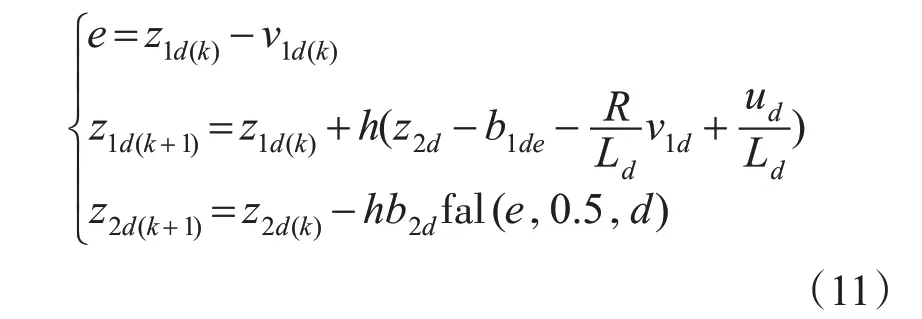
NLSEF：

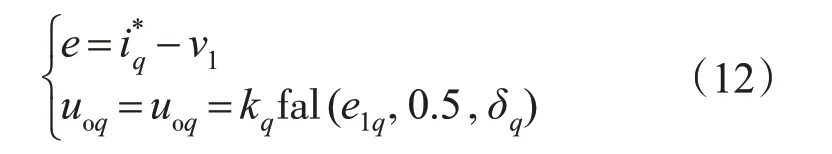
扰动补偿

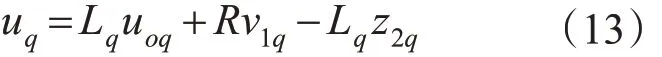
3.2 速度控制系统设计

3.2.1 ADRC+PID组合算法

凡是可以利用经典PID 控制的控制系统，只要可以数字化，从理论上讲，都可以利用ADRC实现。文中针对q 轴电流内环分别采用了一阶ADRC 与PID 控制算法，而d 轴电流则仍然采用ADRC，当系统采用“ADRC+PID”组合算法时，结构框图如图5所示。

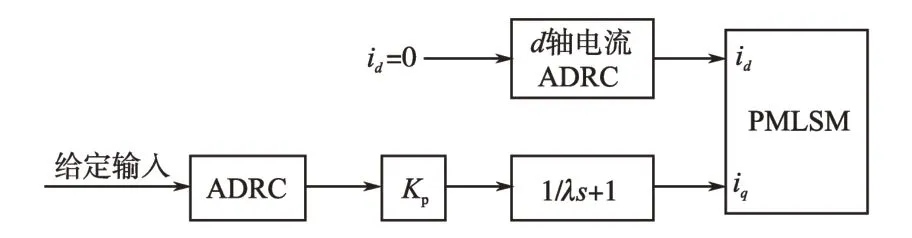
图5 ADRC+PID控制原理框图Fig.5 Control block diagram of“ADRC+PID”

图5 中，速度环采用ADRC 策略，由于与速度外环的时间常数相比，iq内环的时间常数很小，因此针对iq内环采用比例控制，同时考虑到驱动电路所带来的滞环效应，则q 轴电压可以表示为

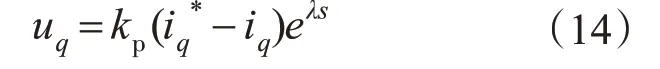
在进行系统设计时，由驱动所带来的滞后效应采用惯性环节来替代，即：

3.2.2 串级一阶ADRC速度控制系统设计

上文设计采用的“ADRC+PID”算法，由于经典PID的引入，导致dq轴之间的强耦合作用未能完全消除，因此速度控制输出仍然存在一定的误差。本文所设计的串级一阶ADRC 如图6 所示，即使用2个一阶ADRC分别实现d轴电流内环与速度外环设计。

图6 串级一阶ADRC控制原理框图Fig.6 Control block diagram of first order ADRC

当控制量取为

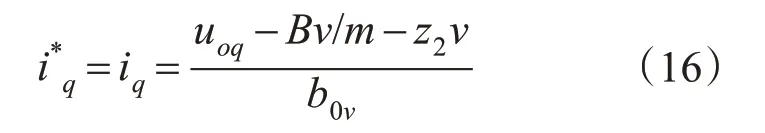
将式（16）代入式（1）则可得：

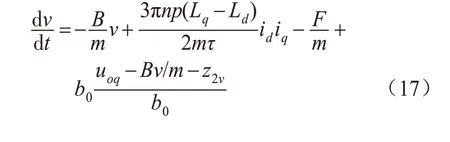
从式（17）可见，利用一阶速度ADRC可以将PMLSM 的速度动态过程改造成为纯积分环节，利用非线性状态误差反馈实现PMLSM的一阶速度ADRC 控制。则PMLSM 一阶速度自抗扰控制算法为

ESO：

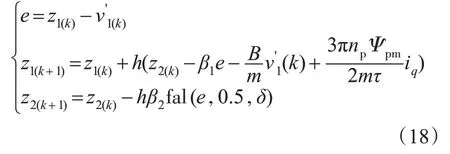
NLSEF：

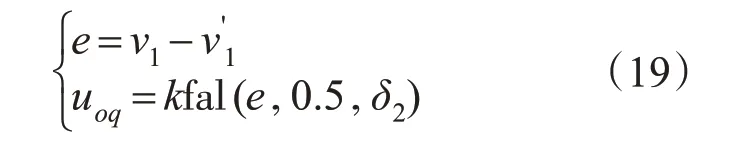
扰动补偿

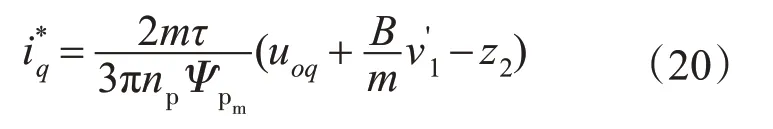
3.2.3 二阶ADRC速度控制系统设计

在串级一阶ADRC 中，采用q 轴电流给定值近似代替实际的q 轴电流，但由于两者间仍存在微小误差，对动态过程的准确跟踪仍有一定影响。针对速度控制进一步设计了二阶ADRC 系统，则将id=0代入电机数学模型中可得：

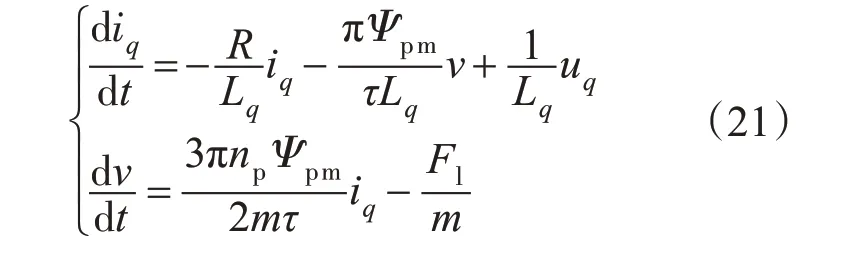
将式（21）中第1项代入第2式则可得到对应的二阶运动方程：

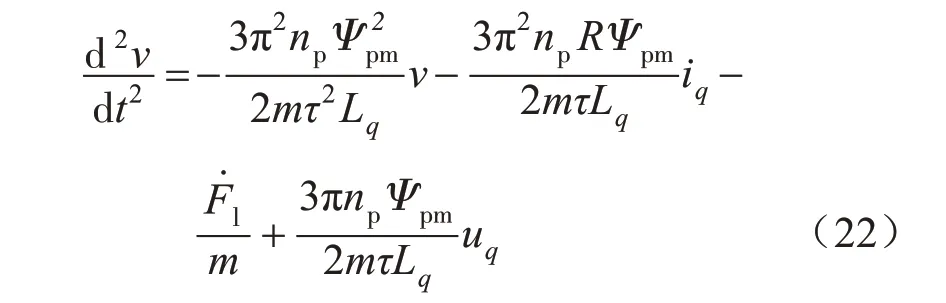
理想情况下，ESO可以通过系统的输入及输出速度实现对未知扰动的准确观测，当控制量取为

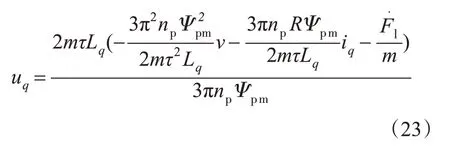
则可得相应的二阶速度ADRC控制算法为

NLSEF：

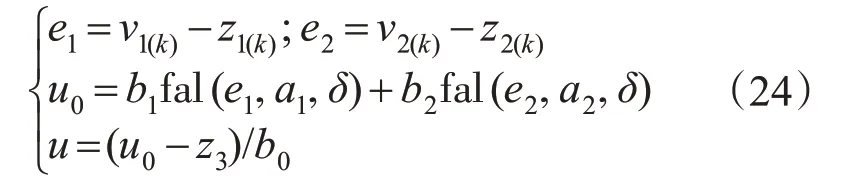
ESO：

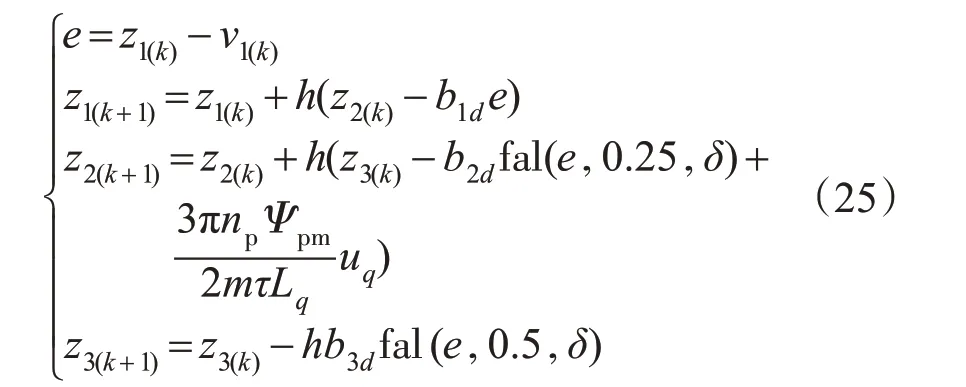
3.3 位置控制系统设计

对实际控制系统而言，系统控制的最终归宿均是使得实际输出准确、快速地跟随目标值的变化。假如系统目标轨迹提前预知，则可以直接利用参考加速度来直接控制系统输出，当采用参考加速度作为前馈信号进行工程实践设计时，为减小外部扰动的观测误差，将前馈控制与反馈控制相结合，前馈通道用来输出目标期望值响应的前馈加速度，反馈通道用来抑制系统中未被准确观测到的外扰作用。如图7所示，其中参数b与b0表达式如下式所示：

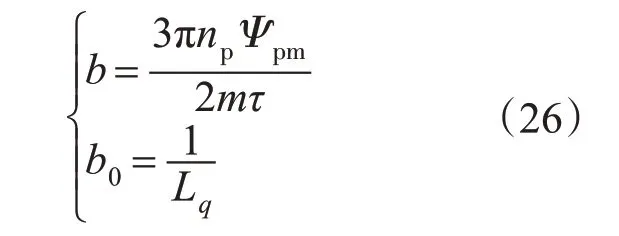
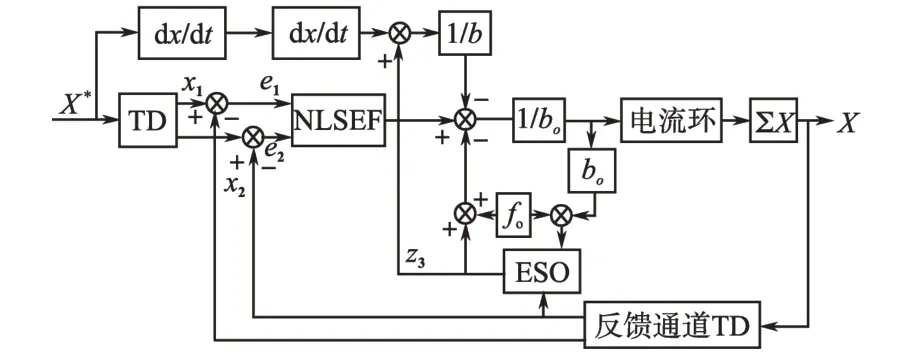
图7 改进型ADRC（MADRC）结构框图Fig.7 Structure diagram of improved ADRC

针对位置自抗扰控制系统，由于从系统控制量到系统实际输出只需要2 个积分器，位置环与速度控制系统类似，只包含了位置外环与电流内环，其中dq轴电流仍然采用上述的ADRC解耦控制，位置外环则采用引入前馈加速度的改进型ADRC控制。

由PMLSM 的数学模型可得其位置动态方程：

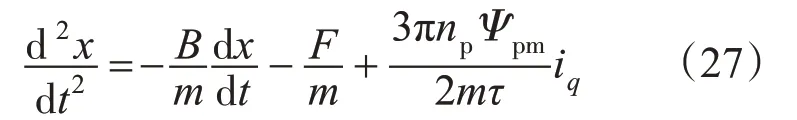
当选取x1=x，x2=v为状态变量，依据式（27），同理可设计相应的二阶位置ADRC为

TD：

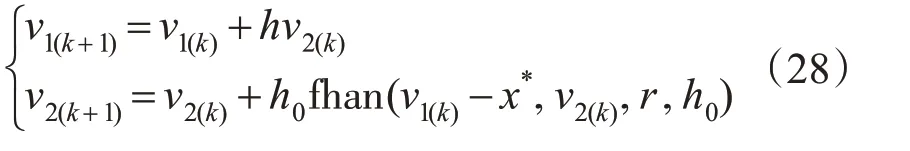
ESO：

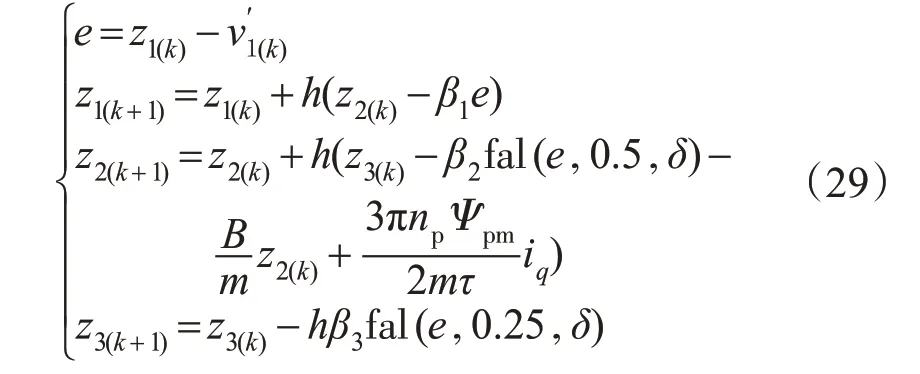
NLSEF：

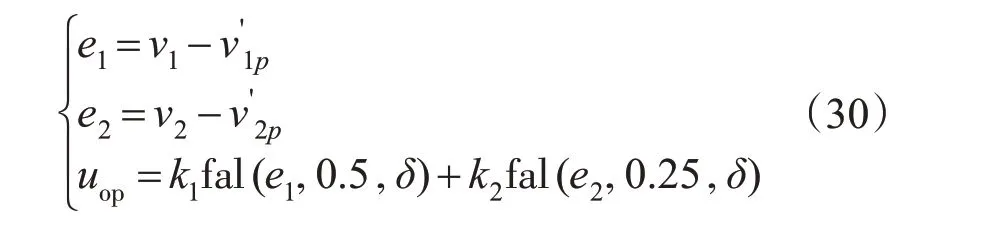
扰动补偿

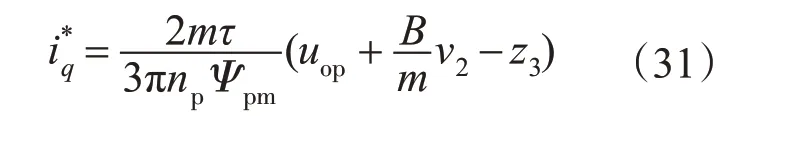
4 仿真分析

4.1 速度ADRC仿真分析

电机仿真参数为：动子质量m=2.85 kg，永磁体磁链Ψpm=0.175 mH，电感Ld≈Lq=8.5 mH，Rs=25 Ω，Fc=40 N，Fs=50 N。给定速度信号为单位阶跃响应，电机空载启动，在0.4/0.9 s突加50 N负载，同时考虑系统所受的外部扰动，针对速度控制系统分别采用ADRC+PID组合算法、串级一阶ADRC、二阶ADRC 与MADRC 进行仿真，图8～图11分别为采用与“ADRC+PID”组合算法、串级一阶ADRC、二阶ADRC 与MADRC 时的速度响应波形。

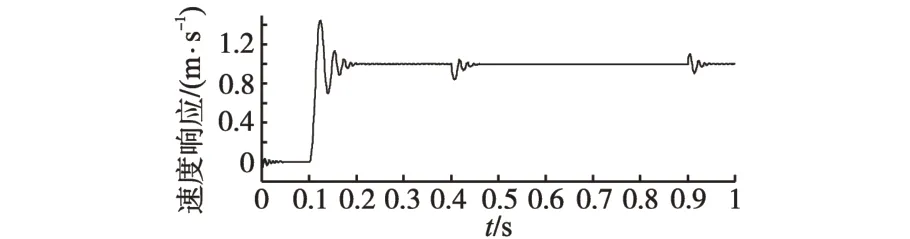
图8 ADRC+PID速度响应波形Fig.8 Speed response waveform of“ADRC+PID”

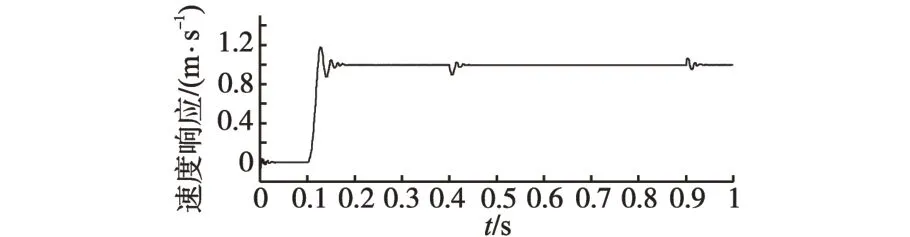
图9 串级一阶ADRC速度响应波形Fig.9 Speed response waveform of ADRC

从上述图中可以看出当采用“ADRC+PID”组合算法时，由于dq轴之间存在的强耦合作用不能完全消除，因此速度控制输出仍然存在一定的误差，与采用串级一阶ADRC 控制相比较，采用“ADRC+PID”组合算法的控制方式，所涉及的ADRC 参数较少，适用于控制系统性能不是特别高的场合。

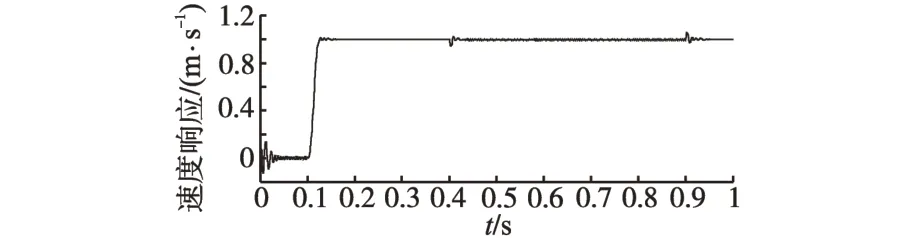
图10 二阶ADRC响应波形Fig.10 Speed response waveform of second order ADRC

从图10 可以看到系统在空载启动阶段系统有较大的波动，速度误差较小，为避免波动较大，可以通过引入反馈通道TD 来实现，其仿真结果如图11所示。

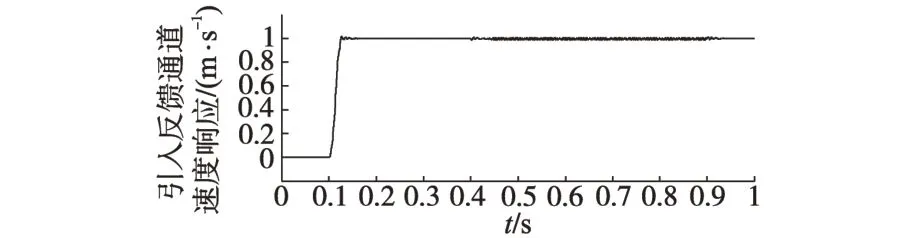
图11 二阶MADRC响应波形Fig.11 Response waveform of second order MADRC

在不改变ADRC参数的同时，将电机动子质量M增大50%，Rs增大50%。通过系统仿真，从图12 可以看出，当本体参数发生变化时，且在ADRC 可承受的范围之内，其控制性能良好，基本可以满足控制系统的性能指标要求。

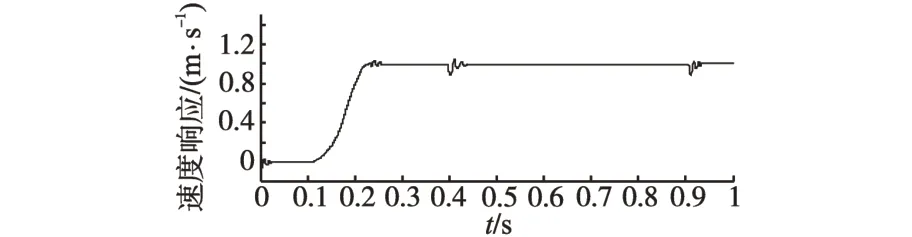
图12 速度响应波形Fig.12 Speed response waveform

4.2 位置ADRC仿真分析

文中针对直线电机位置控制系统，系统给定输入信号为x=1+sin[30t-(0.5π-0.1)]同速度控制系统相同，位置控制系统中也考虑系统所受外部未知扰动及摩擦力的影响，分别对位置控制系统采用传统的二阶ADRC 与MADRC 控制策略进行系统仿真，位置响应波形及跟踪误差波形如图13～图15所示。

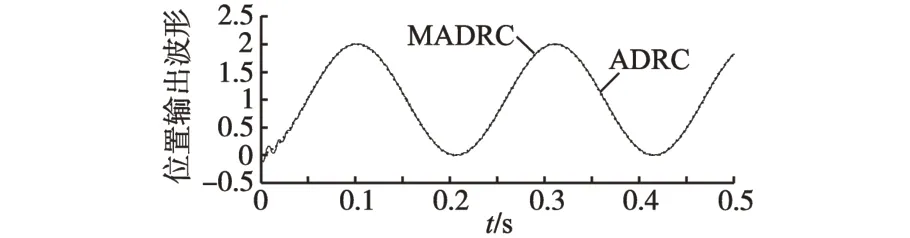
图13 ADRC，MADRC位置控制输出波形Fig.13 Position output waveform of ADRC，MADRC

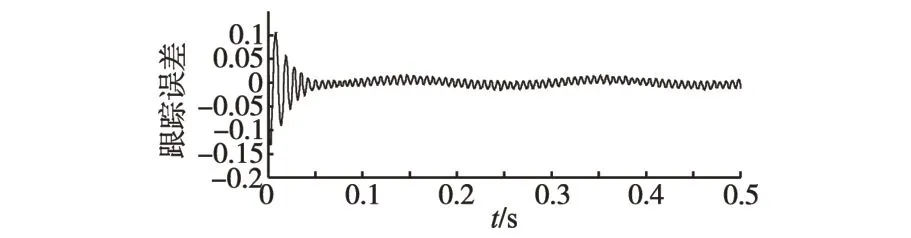
图14 MADRC跟踪误差波形Fig.14 Tracking error waveform of MADRC

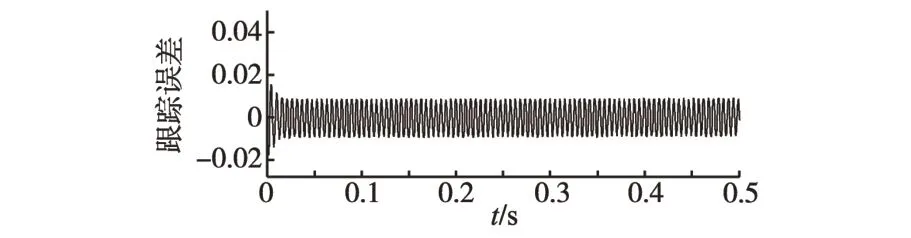
图15 ADRC 跟踪误差波形Fig.15 Tracking error waveform of ADRC

图13 为采用ADRC与MADRC时，位置输出跟踪波形。从图13中可以看到，在采用ADRC控制时，位置输出响应经过0.06 s左右达到稳态，在0.02 s 时，其输出误差达到峰值0.12，在到达波峰与波谷时，误差会有极小的增大。由图14 与图15对应的跟踪误差波形可以看出，采用ADRC控制时，系统响应较快，经0.05 s 左右可达到稳态，系统输出误差最大值可达到0.1左右；当MADRC时，基本不存在超调现象，响应速度更快且误差很小，仿真结果表明MADRC 具有良好的控制性能。

5 结论

针对直线电机强耦合、非线性、多变量的特点，提出了基于ADRC 的dq 轴电流解耦控制，同时，结合ADRC策略，给出了直线电机自抗扰控制系统详细的理论分析与设计思路，搭建了完整的仿真模型并针对速度控制系统分别采用了串级一阶ADRC、“ADRC+PID”组合算法、二阶ADRC算法进行了仿真验证，仿真结果表明在满足系统快速响应的同时，其超调量较小，具有良好的鲁棒性；针对位置控制系统，在带有反馈通道的改进型ADRC 算法的基础上，引入参考加速度作为前馈控制量，构建了基于MADRC的位置控制系统，仿真结果表明采用该设计方法时系统响应快速，跟踪误差小，具有良好的控制性能。由此证明了文中所提出的自抗扰控制方案的可行性，验证了自抗扰控制器具有较强的适应性和鲁棒性。值得说明的是，文中侧重于直线电机ADRC系统的理论推导与设计，尚缺乏一定的系统实验支撑，控制系统实验平台的调试运行将是今后工作的重点。

［1］ 朱骁，党选举，徐小平.永磁直线同步电动机的改进型迭代学习控制［J］.电气传动，2012，42（10）：54-58.

［2］ 刘川，朱非甲，马伟，等.直线电机的线性自抗扰控制［J］.电机与控制技术学报，2013，17（1）：71-76.

［3］ 杨福广，李贻斌，阮久宏.基于ADRC 的低速位置伺服系统及其仿真［J］.山东大学学报，2009，39（6）：48-52.

［4］ 陈诚，李世华，田玉平.永磁同步电机调速系统的自抗扰控制［J］.电气传动，2005，35（9）：80-85.

［5］ 汪常明，张雷，胡书举，等.基于自抗扰控制器的电动变桨伺服控制技术研究［J］.电气传动，2013，43（3）：45-48.

［6］ 刘希喆，吴捷.永磁直线同步电动机速度环自抗扰控制器的设计［J］.电工技术学报，2004，19（4）：6-11.

［7］ 薛树功，翟成明，魏利胜.永磁同步电机自抗扰控制研究［J］.安徽工程大学学报，2011，26（04）：44-47.

［8］ 滕福林，胡育文，李宏胜，等.基于自抗扰控制器的交流位置伺服系统［J］.电气传动，2011，41（11）：46-51.

［9］ 唐小琦，白玉成，陈吉红.永磁同步电机高性能电流解耦控制的研究［J］.电气传动，2009，39（10）：14-18.

［10］闫光亚.永磁直线同步电机自抗扰控制系统及实验研究［D］.武汉：华中科技大学，2011.

［11］汪常明，胡书举，赵斌.基于DSP 的自抗扰控制器算法实现［J］.电气传动，2014，44（1）：68-72.

［12］李忆.自抗扰控制器技术在啤酒发酵罐温控中的应用［J］.电气传动，2010，40（3）：63-65.