基于离散小波变换的气固两相流参数检测

黄 峰,杨道业,孙心岑，史华莹，李 鹏

(1．南京工业大学自动化与电气工程学院，江苏南京 211816；2．91423部队，辽宁大连 116043)



基于离散小波变换的气固两相流参数检测

黄 峰1,杨道业1,孙心岑1，史华莹2，李 鹏1

(1．南京工业大学自动化与电气工程学院，江苏南京 211816；2．91423部队，辽宁大连 116043)

针对传统电容式传感器灵敏场分布不均匀的缺点，设计了双层螺旋电极电容式传感器，并且通过有限元仿真分析传感器结构参数对灵敏场分布的影响。对传统的相关时延估计算法进行了改进，提出了基于离散小波变换的相关时延算法，并将其应用到气固两相流速度测量当中，将两种算法测量结果进行了对比。实验证明，与传统的时延算法相比，基于离散小变换的相关时延算法具有更强的压制信号噪音能力，在低信噪比情况下也能准确进行时延估计。

双层螺旋电极电容式传感器；离散小波变换；气固两相流；有限元；灵敏场分布

0 引言

气固两相流是两相流体系中典型的流动形式，广泛应用于食品加工、石油提纯、多相流泵等[1]众多工业生产中。流体流速和固相浓度是气固两相流体系的两个重要参数，但由于其自身的随机性和复杂性,目前已限制了气固两相流检测技术的发展。

电容法是检测气固两相流参数的有效方法，它成本低、响应快，且具有非侵入性，适用范围广，因此被广泛应用于工业生产过程中。然而，电容传感器的敏感场具有“软场效应”，存在灵敏度[2]分布不均匀的问题。

气固两相流体系中，相关法流体流速测量的关键是时延估计，对于时延估计目前主要采用的方法有：广义相关时延估计法[3]、基于相位谱的时延估计法[4]和自适应时延估计法[5]。这些算法虽能计算出时延，但是本身也存在不可忽略的缺点。例如：广义相关时延估计法易受非高斯有色噪音的影响，而自适应时延估计法虽然能够解决对信号和噪音先验知识的依赖，但算法本身计算量大、收敛速度慢。且这些算法都具有难以用于处理非平稳信号的缺点。

本文提出了一种改进的双层螺旋电极电容式传感器。用有限元方法分析了传感器结构参数对灵敏场的影响，计算得到了传感器参数的最优配置。根据最优配置参数制作出双层螺旋电极电容式传感器，并将双层螺旋电极电容式传感器应用于气固两相流参数检测系统中。从螺旋电极提取管内固相浓度，并采用相关算法从传感器的两路电容信号中提取固相流速。针对传统相关时延算法的不足，提出了基于离散小波变换的相关时延算法。将改进后的新算法应用到气固两相流参数检测系统中，通过对实验数据处理结果的对比，验证改善后算法的可行性和高效性。

1 双层螺旋电极电容式传感器的设计

1．1 双层螺旋电极电容式传感器结构及有限元仿真

为了提高传感器灵敏场分布的均匀性，降低检测结果对流体流型的依赖，设计了一种双层螺旋电极电容式传感器[6]。该传感器系统主要由绝缘管道、测量极板(检测极板和激励极板)、保护极板和屏蔽罩四部分组成。图1是传感器的截面示意图，图中R1、R3、R2分别对应的是管道内半径、管道外半径和屏蔽罩内半径，α是极板张角。图2是双层螺旋电极电容式传感器的三维立体图,图中激励极板和检测极板对称分布于管道外壁，激励极板、检测极板和保护极板沿着管道轴向方向旋转180°。与其他电容传感器相比，该传感器采用双层检测板结构，可直接根据相关算法计算流体的速度。

图1 双层螺旋电极电容式传感器截面示意图

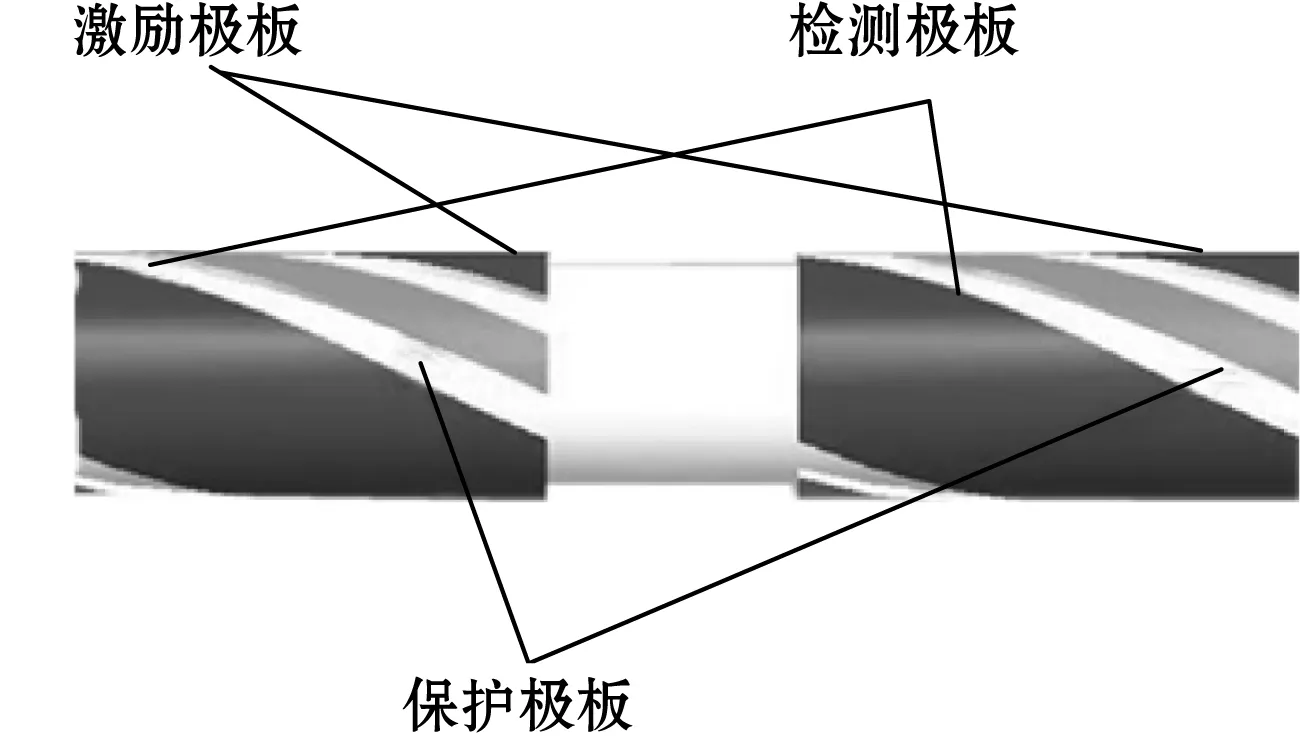
图2 双层螺旋电极电容式传感器三维立体图

1．2 传感器的优化目标函数

采用有限元[7-8]分析传感器结构参数对传感器性能的影响。灵敏场分布的均匀性是衡量传感器性能的主要指标。为有效地评价灵敏场分布的均匀性，引用均匀性误差参数Svp的概念，其描述为[9]

(1)

式中：Savg为各单元相对灵敏度的平均值；Sde为各单元相对灵敏度的标准差。

均匀性误差参数Svp反映了检测场灵敏度分布情况，其值越小，则灵敏场越均匀。

1．3 传感器结构对均匀性误差参数的影响

图3是传感器的3个结构参数对Svp的影响，纵坐标表示Svp的值，横坐标分别表示的是径极比、管壁介电常数、极板张角的值。从图3(a)中可以看出，随着径极比η(管道内半径与管道外半径的比值)的增加，Svp先减少后增大，当η=0．714时，Svp最小。所以在满足机械强度的要求下，管壁厚度应适当薄一点。图3(b)是管壁介电常数对Svp的影响。随着管壁介电常数的增加，Svp也逐渐增加。所以管壁材料的介电常数越小越好。图3(c)为极板张角对Svp的影响，随着极板张角的增加，Svp呈现先减小后增大的变化趋势。在极板夹角φ=135°时，Svp取得极小值，灵敏场分布最为均匀。经仿真优化选取εpipe=4，φ=135°，η=0．875为最优参数。

2 基于离散小波变换的相关时延算法

2．1 相关时延算法

气固两相流参数测量的准确性高低在于时延估计的精度，对于时延估计，一般是使用相关时延算法[10]对信号进行互相关计算以提取时延。

设双层螺旋电极电容式传感器上下两极板检测到的电容信号分别为x1(t)、x2(t)，则有：

x1(t)=s(t)+ω1(t)

(2)

(a)

(b)

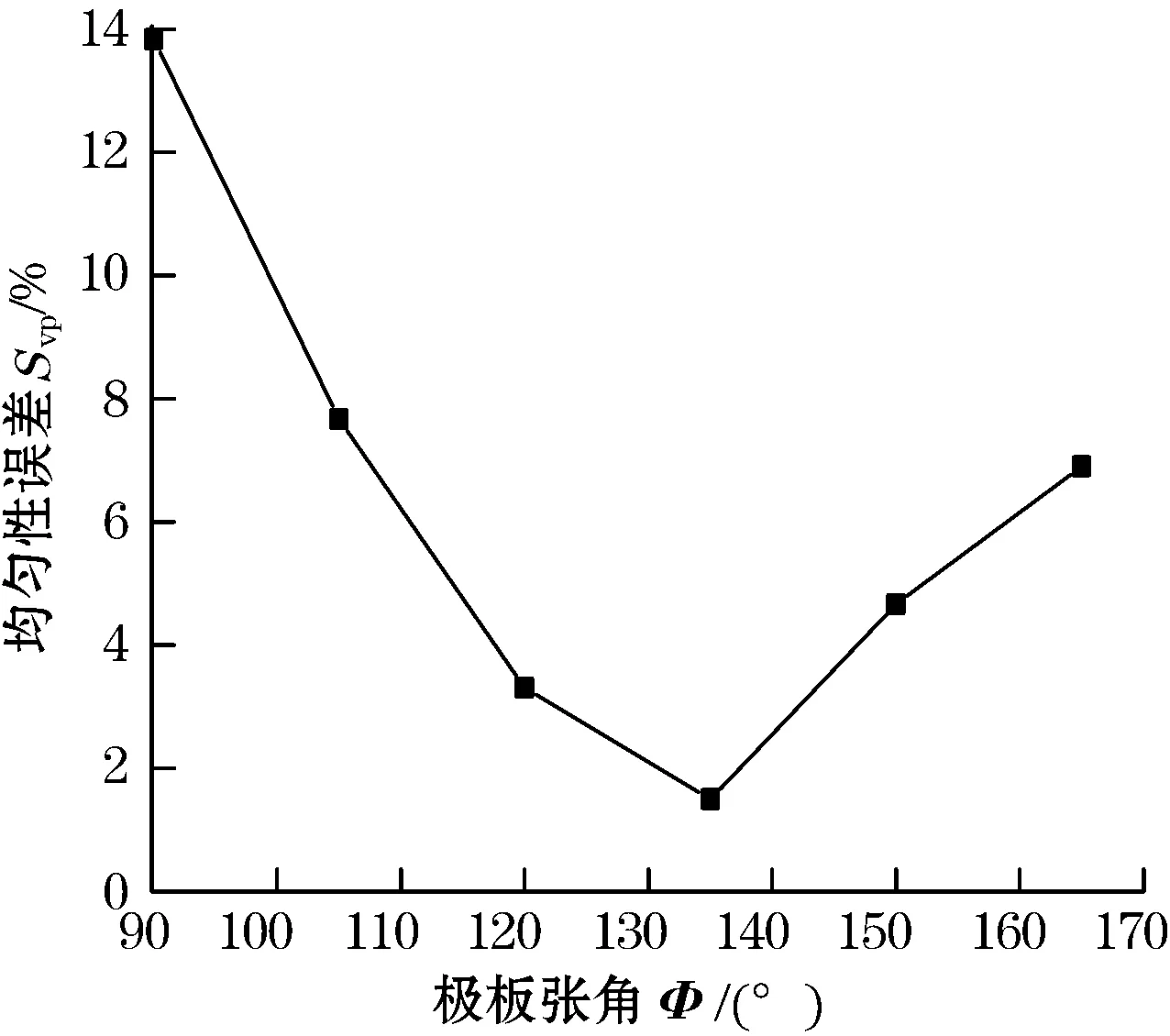
(c)图3 传感器各结构参数对均匀性误差的影响

(3)

式中：s(t)为源信号；ω1(t)和ω2(t)为相互独立的零均值方差为1的高斯白噪音；α为信号的衰减系数；T为延迟的时间。

x1(t)和x2(t)的互相关函数为

Rx1x2(τ)=E{x1(t)x2(t+τ)}=αRss(τ-T)

(4)

因为|Rss(τ)|≤|Rss(0)|，所以Rx1x2(τ)在τ=0处取得最大值，即τ-T=0时，Rx1x2(τ)达到峰值，根据Rx1x2(τ)的峰值就可以求出对应的时延T。此算法简单快速，但是对非平稳信号处理结果较差。为了弥补这一缺陷，本文引入小波变换，在对信号相关计算前利用小波变换对信号进行滤波处理，以提高时延估计的精度。

2．2 基于小波变换的相关时延算法

小波变换[11-12]克服了傅里叶变换的整体性，提供了一个随频率改变的时间—频率窗口，能同时表征信号的时间和频率信息，是处理非平稳信号的强有力工具。

设x(t)为输入信号，则x(t)的连续小波变换实质就是使用一个单位冲击响应对x(t)进行输出。单位冲击响应的时频窗函数为：

(5)

式中：Ψa,b(t)称为小波函数；a为伸缩因子；b为平移因子。

则x(t)的连续小波变换为：

(6)

从系统响应角度来看，x(t)的连续小波变换就相当于是用一系列的带通滤波器对x(t)进行滤波输出，Wx(a,b)中的a反映了带通滤波器的中心频率和带宽，b为滤波后的输出时间参数。从频域上看，不同尺度的小波变换相当于用一组带通滤波器对x(t)进行处理。在实际应用中，大多数信号都为离散信号，这时就需要对小波函数Ψa,b(t)进行离散化，一般取a=2j，b=k2j，则离散化后得：

Ψj,k(t)=2-j/2Ψ(2-jt-k)

(7)

φj,k(t)=2-j/2φ(2-jt-k)

(8)

式中φ(t)与Ψ(t)分别称定标函数和子波函数，{φj,k(t)}与{ψj,k(t)}为两个正交基函数的集合。

记P0f=f在第j级上的一维离散小波变换通过正交投影Pjf与Qjf将Pj-1f分解为：

(9)

(10)

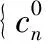
信号x(t)的离散小波变换就是在2j尺度上分解提取出信号的高低频系数。噪音一般都是出现在高频部分，对信号的高频系数进行软阈值处理，对处理重构后的信号y1、y2进行互相关计算，得到互相关函数Ry1y2(τ)。据Ry1y2(τ)的峰值,求出时延T。互相关函数可以表示为：

(11)

3 仿真与实验

根据双层螺旋电极电容式传感器搭建气固两相流多参数检测平台。实验检测对象为直径2 mm,相对介电常数为3．5的玻璃珠作固相介质。料罐在出料过程中重力发生变化，3路重力传感器将采集到的重力值放大转换为数字信号，通过RS485传给上位机，上位机对数据进行处理提取出固相质量流量。图4为内径36 cm垂直管道内颗粒运动过程中料罐内玻璃珠颗粒的质量和质量流量曲线，横坐标表示采样时间，左边纵坐标表示出料过程中，经过电容传感器两极板时的瞬时质量流量，右边纵坐标表示出了过程中，料罐内的玻璃珠质量。由图4中可知玻璃珠颗粒的总质量为50 kg，出料过程曲线呈线性关系。输送刚开始时质量流量慢慢变大，稳定后值是1．071 kg/s。

图4 玻璃珠质量监控曲线

双层螺旋电极电容式传感器采集玻璃珠经过电容极板时的电容值，传感器上下两极板之间距离是4．5 cm，传感器的上下两个测量极板轴向长度是9 cm，传感器的采样频率是9 kHz。每次取上下两极板采集的连续1 024个电容值进行一组小波变换相关时延计算。

小波变换中小波基的选取具有不唯一性，且不同的小波基对信号处理结果不一样。通常用于信号处理的小波有Haar小波、Daubechies(dbN)小波、Coiflet(coifN)小波等。在进行大量的实验及理论分析后，选择dbN小波作为整个实验的小波基。因为dbN小波存在离散小波变换，具有正交、紧支撑性，且正则性随着序号N的增加而增加。但同一信号经过不同类型的dbN小波的不同层数分解处理后，结果也会存在细微的偏差，为了提高测量时延的精度，本次实验对不同类型dbN小波的不同分解层数进行多次实验，寻找适合本次实验的最优配置。

3．1 分解层数对信号处理结果的影响

首先从双层螺旋电极电容式传感器采集到的电压值中选取1 024个作实验，采用db6小波作为小波基，分别进行三层、五层、六层分解，采用默认阈值法进行软阈值处理，把处理后的系数进行重构。将不同层数分解处理后的结果与原始信号作对比，来获得最优分解层数。

图5中横坐标表示的是采样点数，纵坐标表示采样点所对应的电容值。从图5(b)可发现毛刺和突变严重原始信号，在经过db6小波的三层分解后得到了一定的优化，但还存在轻微突变，且信号不稳定；图5(c)和5(d)中信号经过五层分解后已基本去除了干扰，曲线也很平滑,六层分解虽然有效地去除了干扰信号，但是也滤除部分有用信息，使信号失真。所以最佳分解层数选取五层。

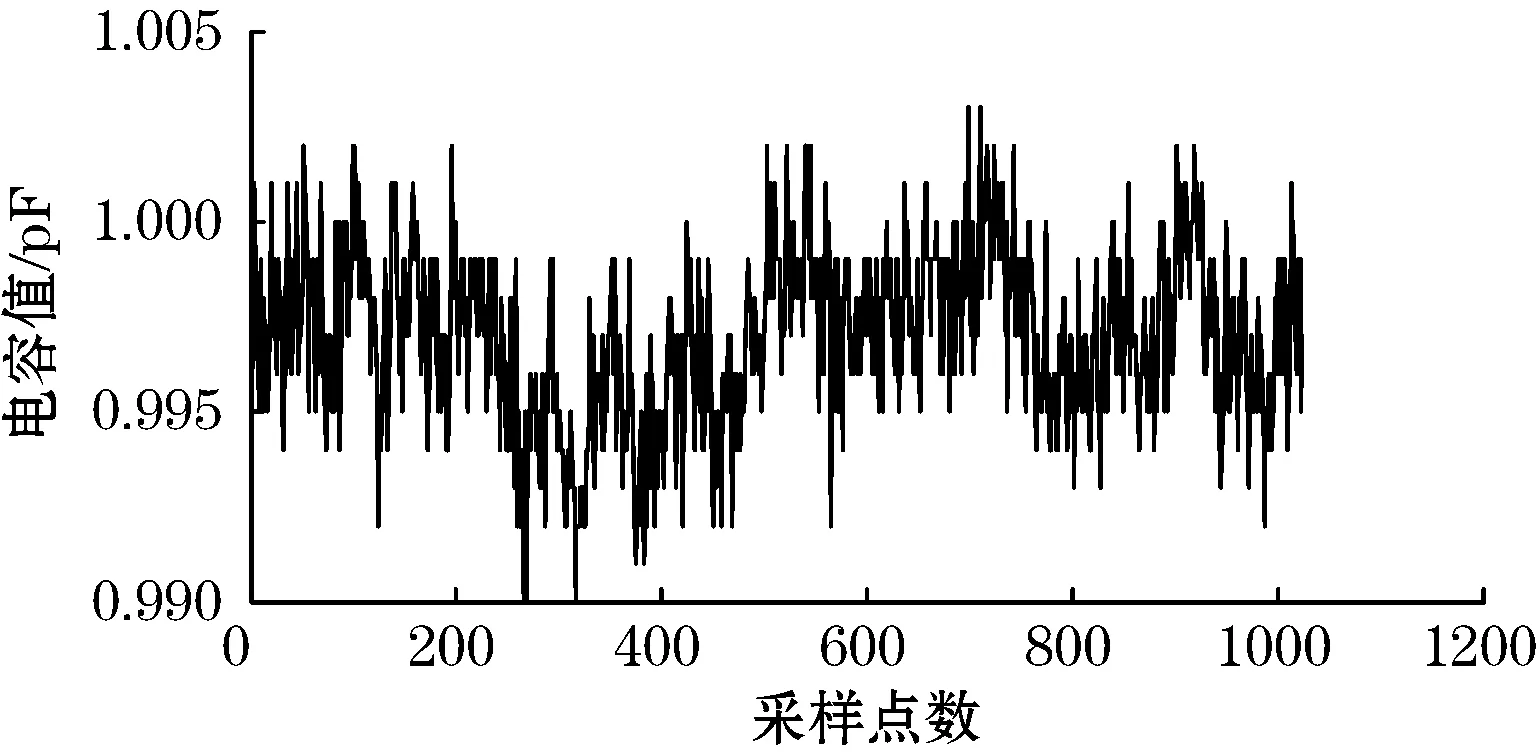
(a)源信号

(b)db6小波的三层分解重构信号

(c)db6小波的五层分解重构信号

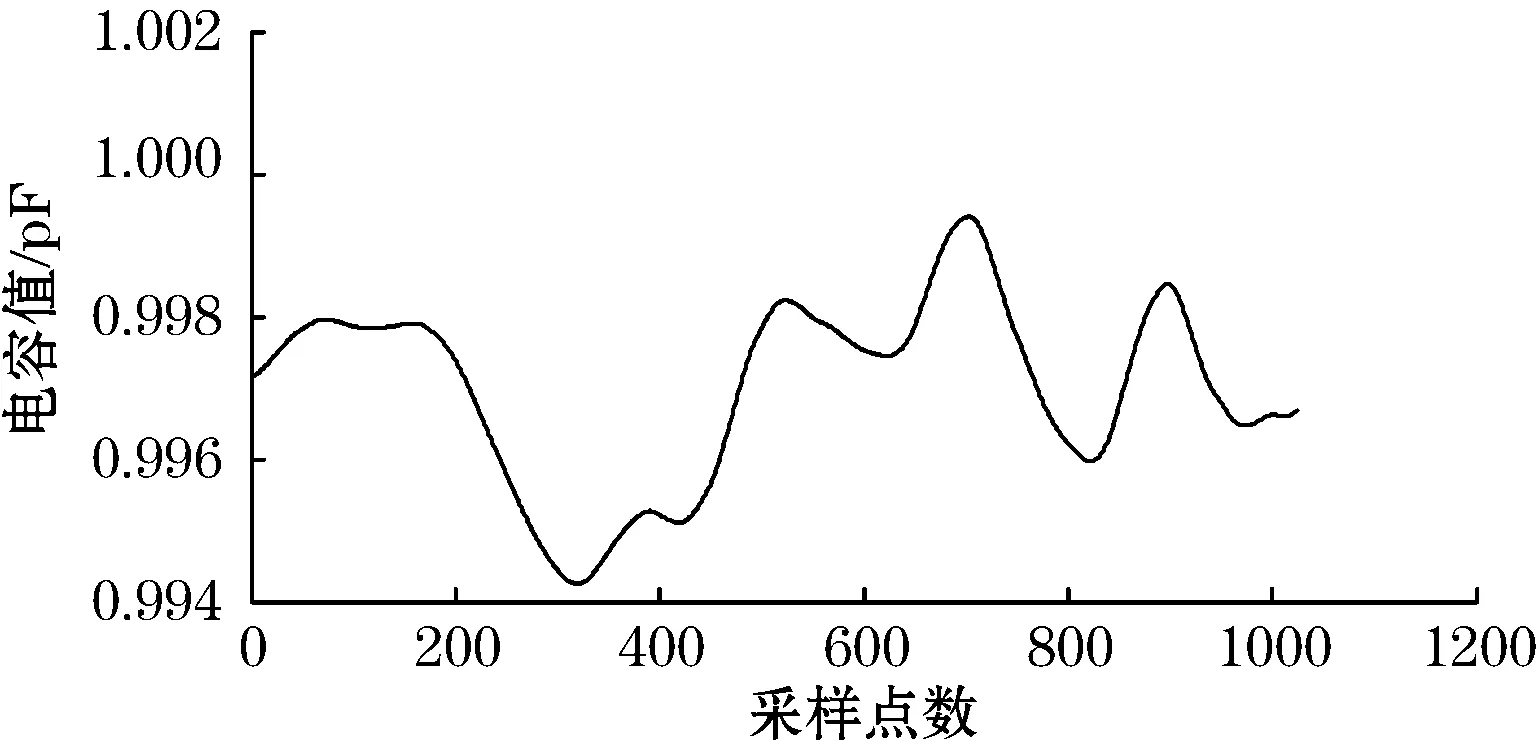
(d)db6小波的六层分解重构信号图5 Db6小波对信号的N层分解处理结果

3．2 不同dbN小波对信号处理结果的的影响

固定分解层数为五层，改变小波类型来探讨不类型的dbN小波对信号处理结果的影响。

由图6可知，源信号是带有干扰且突变比较严重的信号，在经过db3小波的五层分解后滤除了一部分干扰信号，但是信号不平滑，且丢失了部分有用信息；db5和db8小波五层分解后的信号不仅滤除了干扰信号，且平滑性也很好；对比图5的结果选择db6小波五层分解作为最优配置。

(a)源信号

(b)db3小波的五层分解重构信号

(c)db6小波的五层分解重构信号

(d)db8小波的五层分解重构信号图6 DbN小波对信号的五层分解结果

3．3 最优配置下两种算法求得流速的比较

将电容传感器测得的所有电容值根据两种不同的算法分别求速度。如图7所示，横坐标代表采样时间，纵坐标表示每个采样时间点所对应的质量固相流速。由图7中可知，基于离散小波变换的相关时延算法求出的流速，在稳定性方面要高于相关时延算法。

(a)基于离散小波变换的相关时延算法求得的流速

(b)相关时延算法求求得的流速图7 两种算法处理后的速度对比

3．4 基于离散小波变换的相关时延算法准确性的验证

本次实验中管内流体采用了直径2 mm的石英玻璃珠颗粒作为固相原料。使用不同算法，求出玻璃珠颗粒自由落体状态下，经过传感器测量极板时的瞬时速度，利用电容归一化法[13-14]求得对应的瞬时浓度，结合速度值进一步求得质量流量。将不同算法算出的流量值与重力传感器测得的质量流量值作对比。图8为不同途径下得到的质量流曲线，表1为不同条件下两种算法处理结果与重力传感器所测质量流量的比较，可清楚看到基于离散小波变换的相关时延算法求出的质量流要比直接相关算法求出的更加接近实际值，尤其是db6小波的5层分解求出的值最接近重力传感器所测值，误差只有9．06%。

图8 不同途径求取的质量流曲线图

测量方法小波分解层质量流/(kg·s-1)误差/%基于离散小波变换的相关时延算法db350．91714．39db550．90515．42db850．90115．58db630．89716．24db650．9749．06db660．95211．11相关算法0．87218．58重力传感器1．0710

4 结束语

本文构建出一种新型的双层螺旋电极电容式传感器，引入目标函数Svp来分析传感器的径极比、管壁介电常数、极板张角对灵敏场分布的影响。分析了传统相关时延估计算法的不足，提出了基于离散小波变换的相关时延算法，并且对改进后算法的准确性进行了验证。将改进后的电容传感器和算法应用到气固两相流参数检测系统中，准确测出了固相流量。

双层螺旋电极电容式传感器与基于离散小波变换的相关时延算法相结合，能够较好的对气固两相流参数进行检测，但想要其发挥出最大效用还需注意以下几点：

(1) 传感器的3个结构参数中，管壁厚度对Svp的影响最大，因此从灵敏场分布的均匀性方面考虑，管壁厚度在满足机械强度的要求下都要尽量薄些。

(2) 基于小波变换的相关时延算法中关键是小波基的选取，它关系到处理结果的好坏。目前主要是通过用小波分析处理后的结果与准确值的误差大小来判定小波基选取的好坏，因此需要通过大量实验来选定小波基。

[1] CHAPLIN G，PUGSLEY T．Application of electrical capacitance tomography to the fluidized bed drying of pharmaceutical granule．Chemical Engineering Science，2005，60(24)：7022-7033．

[2] SU B L，ZHANG Y H．The use of simultaneous Iterative Reconstruction Technique for Electrical Capacitance Tomography．Chemical Engineering Journal，2000，77：37-41．

[3] 铁勇，刘洋，李树华．广义相关时延估计方法在漏水检测定位中的应用．内蒙古大学学报，2007，38(2)：217-218．

[4] 马晓红，陆小燕，殷福亮．改进的互功率谱相位时延估计方法．电子与信息学报，2004，26(1)：54-56．

[5] 郭莹，孟彩云．改进的LMS自适应时延估计方法．沈阳工业大学学报，2013，35(2)：201-202．

[6] 李虎，杨道业，程明霄．螺旋表面极板电容式传感器的灵敏场分析．化工学报，2011，62(8)：2293-2295．

[7] 张倩，胡仁喜．ANSYS 12．0电磁学有限元分析从入门到精通．北京：机械工业出版社，2010：23-40．

[8] 颜华，高静．电容层析成像的仿真研究．系统仿真学报，2003，15(11)：1625-1627．

[9] TOMASZ D，LAURENT F J，ARTURJ．Applications of electrical tomography for gas-solid and liquid-solids flows-a review．Powder Technology，2000，112(3)：174-192．

[10] 行鸿彦，刘照泉，万明习．基于小波变换的广义相关时延估计算法．声学学报，2002，27(1)：88-93．

[11] 周伟．基于MATLAB的小波分析应用．西安：西安电子科技大学出版社，2010：18-25．

[12] 倪豪．小波消噪与分解对结构地震反应的影响：[学位论文]．大庆：大庆石油学院，2004：23-26．

[13] KENNEDY J，EBERHART R．A new optimizer using particle swarm theory．Proceeding Sixth International Symposium on Micro Machine and Human Science，1995：39-43．

[14] KENNEDY J，EBERHART R C．Particle Swarm Optimization．IEEE International Conference on Neural Networks．Perth，1995：17-22．

Parameter Measurement of Gas/solid Two-phase FlowBased on Discrete Wavelet Transform

HUANG Feng1，YANG Dao-ye1，SUN Xin-cen1，SHI Hua-yin2，LI Peng1

(1．School of Automation and Electrical Engineering,Nanjing Tech University,Nanjing 211816,China；2．91423rd Unit of PLA,Dalian 116043,China)

Aiming at the disadvantage of the unevenly distributed sensitive field of the traditional capacitive sensor,the double-deck spiral plate capacitive sensor was designed,and the structural parameters of sensor which impact the sensitive field distribution were analyzed through the finite element simulation．The related time delay algorithm based on discrete wavelet transform was proposed,which improved the traditional cross correlation algorithm．This method was applied to gas-solid two-phase flow rate measurement,and the measurement results were compared with the traditional．Compared with the traditional method of delay algorithm,results show that the correlation delay algorithm based on discrete wavelet transformation has a stronger ability to suppress signal noise．Therefore,this method can accurately estimates the time delay under low SNR．

double spiral electrode capacitance sensor；discrete wavelet transform；finite element；gas-solid two phase flow；sensitivity distribution

林献坤(1975—)，博士，副教授，主要从事精密加工和智能加工技术方面的研究。E-mail:linxk333@126.com 朱琳(1990—)，硕士研究生，主要从事智能测控方面的研究。E-mail:1035676237@163.com

国家自然科学基金项目(51106070)；华东理工大学煤气化及能源化工教育部重点实验室开放课题基金项目

2014-07-10 收修改稿日期：2015-03-08

TP934

A

1002-1841(2015)05-0065-04