机械零件测绘与型线拟合

郭莹莹 芦秀红

(河南省洛阳北方企业集团有限公司，洛阳 471031)



机械零件测绘与型线拟合

郭莹莹 芦秀红

(河南省洛阳北方企业集团有限公司，洛阳 471031)

为对维修备品配件后续加工制造提供准确参数，本文以活塞为例，介绍了精密机械零件轮廓型线的测绘，然后拟合出曲线式的方法，并对测绘和拟合方案进行了不确定度评定。

机械零件；测绘；型线拟合

0 引言

设备维修中经常需要对磨损件进行仿型，以便备用更换。零件的外形多样而复杂，某型摩托车活塞裙部轮廓纵向就呈曲线状。本文对如何进行精密测绘、分析和拟合曲线函数方程进行了探索，并进行不确定度评定，为绘制产品图，投入制造、维修提供了技术支持。

1 待测绘的零件外形分析

某活塞照片如图1。活塞裙部加工精度高，与气缸直接接触并形成最佳间隙，相互高速往复滑动，纵向型线是半径ri关于高度Hi的函数，活塞裙部轮廓相对于中心轴线对称，但并非标准圆柱(测绘结果可证明)。

图1 活塞示意图

2 测绘

2.1 仪器的选择

采用数字式万能测长仪(以下简称测长仪)。选择刃型测头，将刃型测头安装牢固并调整好零位。

2.2 待测绘件安装

将待测活塞压装在测长仪工作台上，注意压板压住内部厚凸台，不要压在外圆薄壁上，以免产生变形，影响测绘。

2.3 测绘

2.3.1 测头与零件接触测点的确定

扳动万能工作台手柄使之倾斜运动，找到最小值拐点，使活塞底部平面保持水平，再转动微分筒使工作台前后移动找到最大值拐点，如此反复2～3次，拐点再无变化时即可在数显上读取活塞截面直径。

2.3.2 实施测绘

转动工作台升降手轮，使刃形测头与活塞裙部上边缘相接触，此处为活塞圆柱面轮廓型线测绘的起始点。读取并记录起始点直径后，以1mm为步长，逐次升降工作台至裙部下边缘，分别读取并记录各截面的直径数值。

2.3.3 数据复核

为保证测绘结果可靠，可采用更换测试员，重复上述步骤，在短时间内进行同一活塞的第二次测量。两次结果的最大差值超出被测直径允差的1/3,应查找原因，进行再次测绘。当无明显差值时说明重复性尚可，即可用测绘数据进行型线拟合。

3 型线方程拟合

3.1 测绘结果进行阶差分析

表1是对某型号摩托车活塞裙部的测绘数据记录。测量时从裙部上边缘(见图1)开始每升高1mm测一个直径Di，计算相应半径为ri,距裙上边缘的高度记为hi，共测得27个截面的直径。对表1测绘数据的分析如下：

因测量时高度h每增加1mm测量一个直径，因此变量h的一阶阶差Δh=1mm为定值。在Δh为定值的情况下，只要用阶差法分析半径ri的几阶阶差趋近于定值，就可以初步判断曲线的趋势，再用最小二乘法拟合就可以了。

当一阶阶差为定值时，高度h和半径r将呈线性关系，图形为直线。本活塞测绘结果一阶阶差明显由大变小，非定值，说明h和r不是线性关系。

当二阶阶差为定值时，高度h和半径r对应于二次函数关系。表1显示二阶阶差均在±0.001内，可视之为定值，说明h和r是二次函数关系。

由表1第3列知，直径Di随hi的增加由小到大，再由大到小，可初步判定曲线形状为椭圆。其中最大值是第10个数据hi=9时Di=52.403，可确定椭圆的两个轴分别是活塞直径(对称中心)和通过hi=9高度的直线。确定hi=9处的新高度坐标H=0，其它截面高度坐标用公式Hi=hi-9计算后分别列于表1的第2列。

3.2 拟合方程

3.2.1 建立通用椭圆方程

椭圆标准方程:r2/a2+H2/b2=1

(1)

设：y=r2，x=H2，A=a2，B=-a2/b2

则：

y=A+Bx

(2)

3.2.2 用最小二乘法拟合椭圆方程

最小二乘法是拟合曲线函数的最佳方法，拟合一次函数方程y=A+Bx的通用公式为：

S(xy)=∑(xi-x均)(yi-y均)

(3)

S(x)=∑(xi-x均)2

(4)

B=S(xy)/S(x)

(5)

A=y均-Bx均

(6)

本例拟合后的函数式是：r2=A+BH2

(7)

(8)

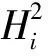
B=S(Hr)/S(H2)=-2362.05/184002

=-0.01284

=686.7757

拟合后的活塞直径函数式为：

(9)

最小二乘法拟合型线方程如表2所示。表2的Ki-Di是按拟合后方程(9)计算的理论直径Ki与实测直径Di的偏差，其绝对值最大值0.016mm，说明拟合的函数式是基本正确的，差值0.016mm应该与被测件的制造尺寸偏差密切相关，应根据实际工艺条件、相关制造标准(如GB/T 1800)酌情对待。

表2 最小二乘法拟合型线方程

4 测量不确定度评定

4.1 被测对象

活塞型线被测参数：为不同高度处活塞型面直径值。详见表1第1、2列Hi和Di值。

4.2 使用的测量设备

数字式万能测长仪：查使用说明书其示值允差Δ≤(1+L/200)μm；经计量校准得到测长仪工作台升降手轮刻度的示值误差为±0.1mm之内。

4.3 测量模型

万能测长仪数显装置读数d即为被测截面的直径D，测量模型为：D=d。

4.4 标准不确定度分量分析

D的测量结果不确定度由直径测得值d引入，d与测长仪示值误差和H定位不准有关。

4.4.1 由测长仪示值误差引入的标准不确定度分量u仪

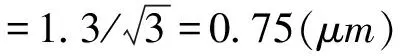
4.4.2 由测量高度H时引入的标准不确定度分量uH

式中，H为距活塞裙边的截面高度；D为活塞在距裙上边缘高度H处的直径。

以最大值H=17为例，cH=-0.4386/26.1353=-0.0168

uH=cH×57.7=0.0168×57.7=0.97(μm)

4.4.3 环境和线膨胀系数引入的标准不确定度分量u环

因为测量是在保持恒温的实验室进行，测长仪膨胀系数以及环境温度引入的标准不确定度分量很小，可忽略不计，u环≈0。

4.5 合成标准不确定度uC

4.6 扩展不确定度U

取包含因子k=2，则U=2×1.2=2.4(μm)。

4.7 不确定度评定的结论

通过不确定度评定可知，本方案扩展不确定度U=2.4μm，k=2。按测量能力指数Mcp=T/2U可得T=2U·Mcp，式中，T为产品参数加工制造允许的误差范围。

原国家计量局推荐一般准确度检验与监控的B级属“配置足够”，应取Mcp≥2～3。取Mcp=2.5，则：T=2×2.4×2.5=12(μm)。

查GB/T 1800.2—2009表1尺寸为50～80mm的标准公差值，IT5公差为13μm，13μm>12μm，说明本文方案满足直径约52mm，公差等级5级及以下的活塞测绘和型线拟合。

5 结束语

随着制造精度的提高，对精密加工零件外观(型线)进行仿形制备的应用日趋广泛深入。上述实例是将最小二乘法原理应用于方程拟合的典型，步骤关键在于拟合。在具体操作中要善于举一反三，根据设备、成本、实际工艺、相关标准及需求等来综合考虑测绘数据重复性、方程拟合方法(最小二乘法是最佳但非唯一方法)，并注意计算中数据修约，总结出适合自身的拟合方法，满足准确、快速的制备要求。

[1] 《数学手册》编写组.数学手册.北京：高等教育出版社，1977

[2] 杨光兴.摩托车发动机设计原理.武汉：武汉测绘科技大学出版社，1993

[3] 李庆忠，李宇红.计量不确定度评估要点.计量技术,2003(1)：46-47

[4] 熊朝晖.随机过程与测量不确定度.计量技术,2007(4)：64-65

10.3969/j.issn.1000-0771.2015.2.10