数字水准仪检定方法的探讨

程鹏里 苏清磊 刘红乐 李 博

(河南省计量科学研究院，郑州 450000)



数字水准仪检定方法的探讨

程鹏里 苏清磊 刘红乐 李 博

(河南省计量科学研究院，郑州 450000)

本文结合笔者在实际工作中的检定经验，主要探讨了数字水准仪电子计量部分的检定。首先介绍了CCD安置状态、系统分辨力、标尺倾斜对测量结果的影响和检定办法，最后重点介绍了i角检定的几种方法，包括富斯特乃尔法、纳保尔法、库卡马可法以及日本方法。

数字水准仪；检定；分辨力；i角

0 引言

水准仪是在测量工作中应用比较多的一种仪器。早期所用的都是普通光学水准仪，1990年徕卡公司首先研制出数字水准仪NA2000。数字水准仪具有读数客观、精度高、速度快、效率高等特点，所以被快速推广并得到广泛应用。数字水准仪是在自动安平水准仪基础上发展起来的，其主要包括光学测量和电子测量两大部分，以往的精密光机型计量标准足以胜任其光学部分的检定工作，新增的以测高和测平距为主要内容的电子计量性能的检定，则需要在室外进行[1]。JJG 425—2003水准仪检定规程主要是针对光学部分进行的检定，对电子测量部分所提并不多。基于此，本文主要介绍了数字水准仪电子计量部分的检定。

1 仪器CCD安置状态及技术参数的检查

数字水准仪是以自动安平水准仪为基础，采用图像处理电子系统的光机电测一体化的高科技产品，它在望远镜部分增加了光电图像接收与处理元件。在观测时，标尺条码一方面被成像在望远镜分划板上，供目视观测；另一方面通过望远镜的分光镜，标尺条码又被成像在光电传感器(CCD)上，并对其进行分析解码并输出显示标尺的高度信息[2]。在数字水准仪中，CCD是其核心器件。理想情况下，CCD(图像传感器)敏感面的中心位置与望远镜准直轴(经分光棱镜反射后)重合[3](如图1)，但是在实际中，安装的CCD存在一定的偏差，所以在对仪器进行首次或修理后的检定时，应首先在专用的检测设备上对CCD的安置状态、仪器的定焦参数等技术参数进行检查。

图1 数字水准仪的测量系统

2 系统分辨力

系统分辩力，也称系统精度，是指仪器与标尺配套使用时，在高度方向上实际能识别的最小高度变化量(应注意系统分辩力与仪器的最小显示值不是同一概念)[4]。电子水准仪没有光学测微器，检验该项目相当于检验电子水准仪的测微能力，实际上是检验电子水准仪图像处理的能力。该项指标一般是归算到每10m视距时的标准偏差。

在室内建立一个可以升降标尺的检验台，检验台下面固定一个螺旋测微装置(如图2)，检验时，把铟钢条码标尺放在升降检验台上，向上或向下移动铟钢条码标尺的量为0.09或0.11mm，共计移动10次，将观测值归算到零点，求其归算量的平均值：

(1)

式中，Hi为铟钢条码标尺在各个位置的高程观测值；hi为铟钢条码标尺在升降检验台上由零点开始改变的距离观测值；则分辨力为：

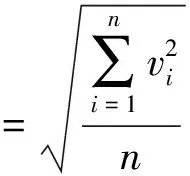
(2)

式中，vi=Hi-H0-hi

图2 系统分辨力检定示意图

3 标尺倾斜的影响

在进行水准测量时，如果标尺倾斜，会使得电子水准仪电子传感器CCD线阵上的像也歪斜[5]。轻则造成读数误差，重则使得仪器无法识别读数。检定标尺在一定的倾斜范围内数字水准仪所读读数对高程的影响具有很重要的意义。

在装载微倾装置的工作平台上，把铟钢条码标尺向左、右、前、后倾斜，多次观测读数，可以发现，在2°以内，对读数变化很小，不超过仪器标称精度；超过2°以后，读数误差急剧上升(如图3、图4)。

图3 标尺前后倾斜时的读数误差曲线

图4 标尺左右倾斜时的读数误差曲线

检定时，在铟钢条码标尺下面装载微倾工作台分别向前后左右各倾斜2°，用电子水准仪进行读数，并和原始数据进行比较，观测其是否超过标称精度。

4 i角的检定

在水准测量中，如果i=0，则水准轴水平(气泡居中)后，视准轴也是水平的，否则视准轴不水平，在读数中对高差产生影响。

4.1i角在读数中的影响

i角使视线向上或向下倾斜，那么设它在A点尺子上的读数较水平视线的读数增大或减小一个Δ值。若A点距仪器的距离为S，则

Δ=S·tani

(3)

当i角的大小不变时，则Δ的大小与S成正比；即尺子离仪器越远，i角对读数的影响越大[2]。现在设有A、B两点，使用水准仪来测量其之间的高差，设

(4)

式中，a′为后视读数；b′为前视读数。则A，B两点的正确高差应为：

(5)

式中，ΔA-ΔB为角在高差中的影响，用ΔhAB表示，即

(6)

显然，当后视与前视的距离相等时，i角对于高差的影响ΔhAB=0，可得到正确的高差；而当后视与前视的距离不相等时，则所测得的高差不正确。

4.2 数字水准仪i角校准的几种方法

传统的平行光管法对于电子水准仪来说只适用于检验光学i角，数字显示的i角校准可以根据其内部设置的程序进行[3]。调用仪器上的校正菜单，可以采用以下4种方法进行校正。4种方法的外业设置如下(如图5～图8)，按照仪器的屏幕菜单提示进行操作，即可完成检验和校正。

1)富斯特乃尔法(Forstnermethod)

如图5，在相距45m处设立两根标尺(A、B)，将此距离分成三等份，并在其连线上设2个仪器站(1、2)，相距标尺约15m，然后从测站量测两个标尺。i角为:

(7)

式中，H1A、H1B、H2B、H2A分别是数字水准仪在(1、2)处所观测的两根标尺(A、B)的读数，S为每等分的距离。

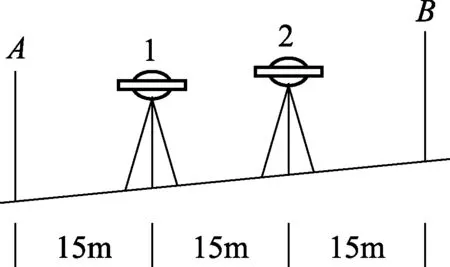
图5 富斯特乃尔法

2)纳保尔法(Nabauermethod)

如图6，量取一段45m长的距离，将其分为三等份，在(1、2)上设仪器，并在距两端1/3处(A、B)立标尺，从测站测量两根标尺。公式同式(7)。

图6 纳保尔法

3)库卡马可法(Kukkamakimethod)

如图7，在距约20m处设两根标尺(A、B)，首先从位于两标尺连线的中间的测站(1)在两标尺上读数。然后从距两标尺连线外延20m处的测站(2)在两标尺上读数。公式为：

(8)

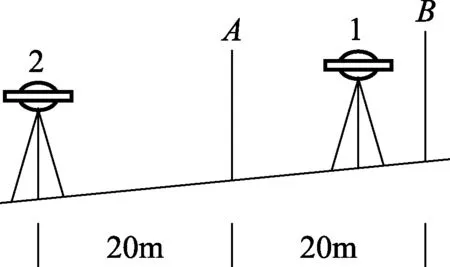
图7 库卡马可法

4)日本方法(Japanesemethod)

如图8，与库卡马可法方法基本相同。然而两标尺(A、B)相距约30m，而测站(1)在(A、B)的中间，测站(2)在标尺(A)后约3m处。公式为：

(9)

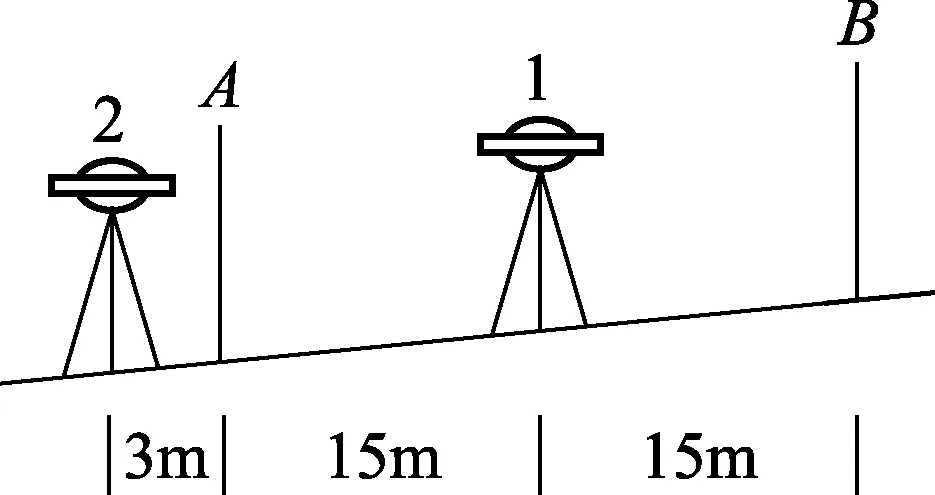
图8 日本方法

5 结束语

通过以上几个项目的校准，再配合JJG 425—2003中对水准仪光学项目的检定，可以实现对数字水准仪全面系统的检定，保证了测量结果的准确可靠，满足了工程测量中对数字水准仪精度的要求，而且对评价数字水准仪的质量和性能也具有一定的借鉴意义，进而促使数字水准仪更加全面和健康的发展。

[1] 李灿.电子水准仪i角误差室外检测的线值表示[J].计量技术，2006(3)：49～50

[2] 张晓.光学成像条码定位理论研究及应用[D].南京理工大学，博士论文，2006

[3] 顾若冰.电子水准仪i角检验校正方法比较研究[J].矿山测量，2008，(4)：15～20

[4] 叶晓明，阙江.数字电子水准仪检定方法的研究[J].测绘通报，2008，(11)：68～70

[5] 耿丽清，李晋惠，程君.电子水准仪水准标尺的条码识别[J].微计算机信息，2005，(21)：132～134

10.3969/j.issn.1000-0771.2015.10.18