钕铁硼永磁体矫顽力的测量不确定度评定*

许志一 张志高 侯瑞芬 贺 建 龚文杰 李小菊 林安利

(中国计量科学研究院，北京 100029)



钕铁硼永磁体矫顽力的测量不确定度评定*

许志一 张志高 侯瑞芬 贺 建 龚文杰 李小菊 林安利

(中国计量科学研究院，北京 100029)

按照GB/T 3217—2013的规定，从闭磁路测量过程和磁参量计算方法入手，以φ10×10mm的钕铁硼永磁体标样为例，分析了影响内禀矫顽力HcJ、矫顽力HcB测量结果的因素，建立了它们的简化数学模型，在此过程中还使用了一些测试技巧和数据处理措施以减小或忽略某些难于确定的方面。结果表明，磁通计、探测线圈、温度测量和测量重复性是对不确定度起主要贡献的方面。

永磁体；钕铁硼；矫顽力；不确定度

0 引言

我国是稀土资源大国，在整个稀土材料应用中，稀土永磁材料占据重要地位[1]。作为第三代永磁材料的NdFeB永磁体，由于其优异的性价比，在过去20多年中得到越来越广泛的应用。我国现有稀土永磁生产企业200家左右，一些正在建设中，主要分布在沪浙、京津和山西等地。

永磁材料的主要技术参数：剩磁Br、矫顽力HcB、内禀矫顽力HcJ和磁能积(BH)max是决定其牌号和使用性能的关键指标，无论是磁体的生产企业还是研发机构，尤其是国家的计量检定测试部门，均要对这些磁参量作出准确可靠的测试，提供高信赖度的磁参量数据。影响磁参量测试结果的因素很多，除了简单的考虑重复性测试结果外，还有诸多涉及设备、测试方法的因素。本文作者曾撰文分析过另一类永磁材料铝镍钴的测量不确定度[2]，而钕铁硼永磁体磁参量的测量方法有所不同，其不确定度分析仍没有公开文献可供查阅。本文依据钕铁硼的测试过程和磁参量计算方法，分析了影响矫顽力的各种因素及其不确定度。

1 测量过程和方法

1.1 磁参量的测量过程

永磁材料的磁性测量遵照GB/T 3217—2013执行[3]，采用闭磁路方式，在回线仪上进行测试。测量装置的基本组成如图1所示。励磁电源E输出磁化电流使磁化装置产生磁化场，通过将磁场从0逐渐增大到最大磁场强度Hmax后，改变磁场方向，使磁场强度从Hmax逐渐变化到负的最大值-Hmax，然后再从-Hmax回到0，经过一个周期的变化，用B(J)线圈与B(J)积分器连接测量磁感应强度B或磁极化强度J，H探头与H积分器连接测量磁场强度H，从而得到一个周期内各磁场强度下的磁感应强度B或磁极化强度J，如图2所示[4]，进而得到各磁参量。对φ10×10mm的NdFeB圆柱标样进行了10次独立测量；用表面温度计测得样品的温度为22.7℃。

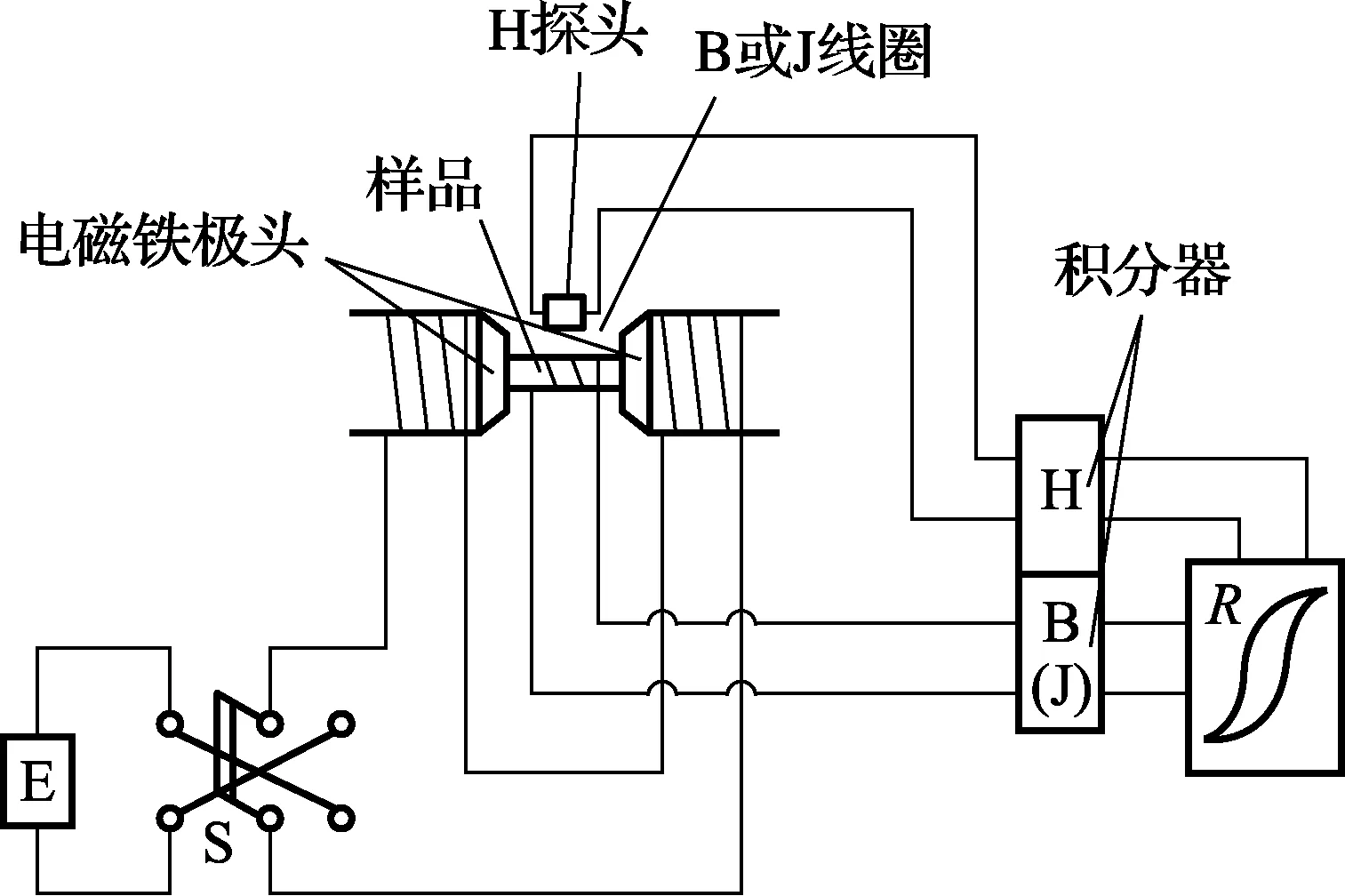
图1 永磁测量装置基本组成示意图

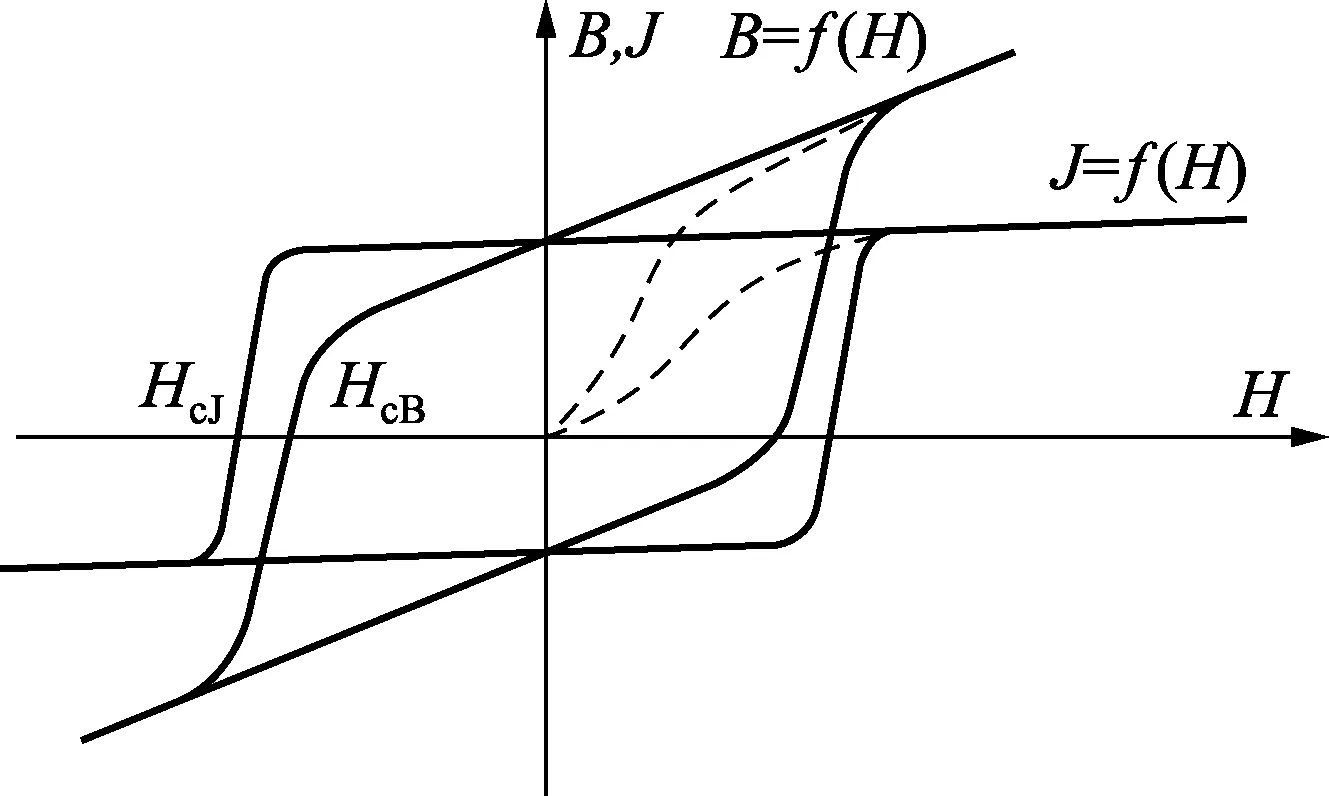
图2 永磁材料的磁滞回线

1.2 矫顽力的计算方法和测量结果

按照GB/T 3217—2013的规定[3]，对于HcJ>600kA/m的永磁材料，磁场强度H是用空心H探测线圈和磁通计测量，利用公式H=Φ/(μ0K)进行计算，其中，Φ是H通道磁通计测得的磁通量；K为H探测线圈常数。同时，利用J线圈测量磁极化强度J，通过公式J=Φ′/(NJAS)计算J值，其中，NJ为有效匝数，AS是试样截面积；若J线圈的残匝面积Γ不为零，则J=[Φ′-μ0HΓ]/(NJAS)。通过采集到的离散J值和H值再由B=μ0H+J可以计算出B值，进而得到J-H和B-H磁滞回线或退磁曲线。如图2所示，HcJ是J-H回线与横轴的交点，HcB是B-H回线与横轴的交点。

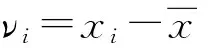
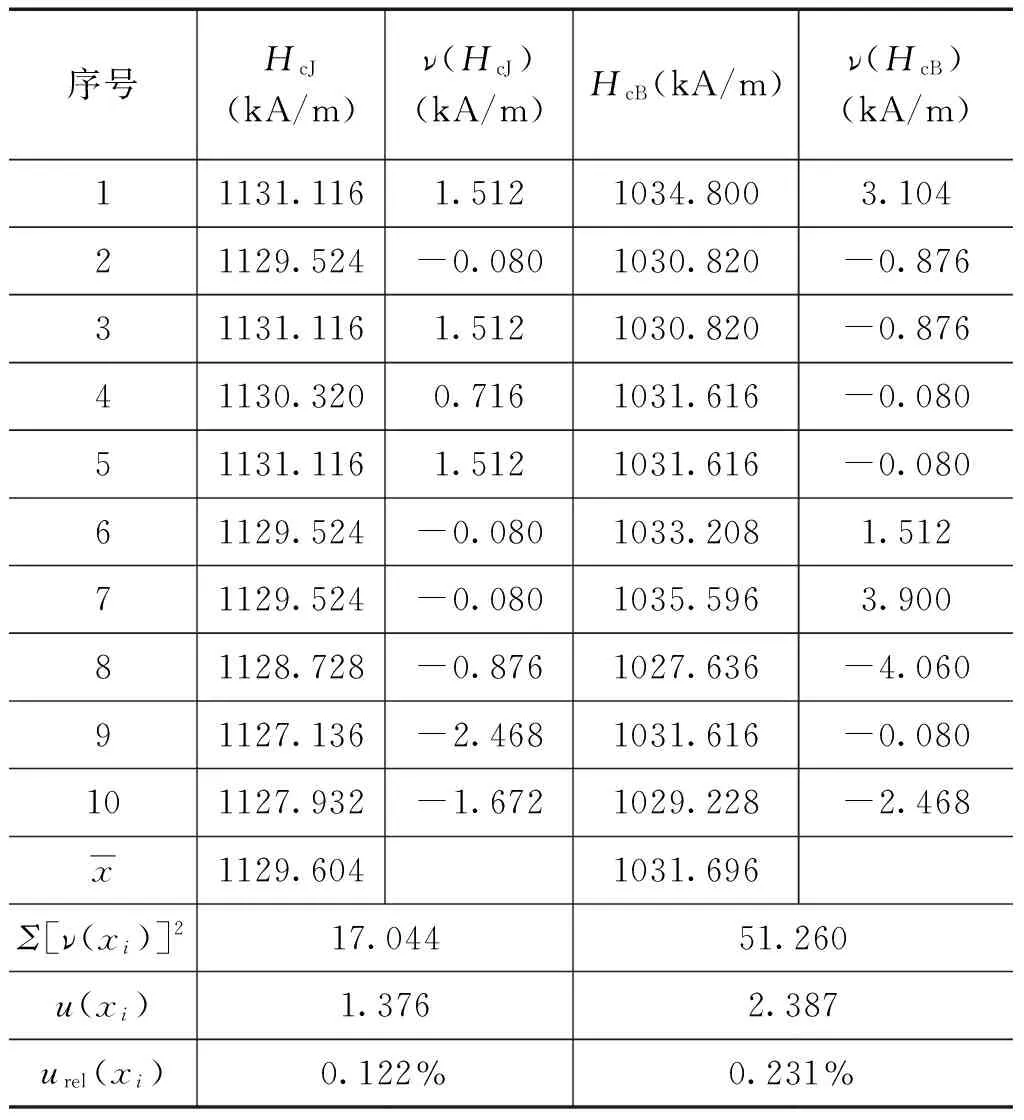
表1 NdFeB标样的矫顽力测量结果

2 矫顽力的不确定度分析

2.1 矫顽力的数学模型

矫顽力Hc(统指HcJ和HcB)的测量结果受测量重复性的影响，温度测量和温度系数影响δT，磁通计校准影响δΦ，偏离正常工作条件的影响δc，其中δc又包括H线圈常数校准的影响δK、H通道磁通计漂移的影响δp、电磁铁磁场均匀区的影响δS、H通道磁通计分辨力的影响δf、试样端面与极头之间气隙的影响δg、退磁速度及J≠0或B≠0的影响δv。

由于各种影响因素难以用数学表达式给出，写出下面的简化数学模型：

2.2 影响矫顽力测量的因素及不确定度分量

2.2.1 H通道磁通计校准的影响δΦ

根据H通道磁通计的检定证书，扩展不确定度U=0.2%，k=3，其相对不确定度为urel(Φ)=U/k=0.2%/3≈0.067%。在使用过程中，通常选择磁通量程在1/2满量程以上，故磁通计校准的相对不确定度urel(δΦ)=2urel(Φ)=0.067%×2=0.134%。

2.2.2 H线圈常数校准的影响δK

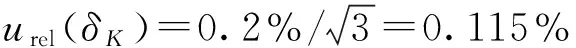
2.2.3 温度及温度系数对H的影响δT

NdFeB的温度系数较大(一般Jr或Br的温度系数a =0.12%/℃，HcJ的温度系数β=0.80%/℃)。认为表面温度计的测得值即为样品的实际温度，忽略测得值与实际温度的差别。测量样品温度所使用的温度计是影响不确定度的主要来源。

校准证书表明，表面温度计的不确定度为U=0.5℃，k=2，则u(T)=U/k=0.5℃/2=0.25℃。因此，温度及温度系数对磁场强度引入的相对不确定度urel(δT)=β×u(T)=0.25×0.80%=0.200%。

2.2.4 H通道积分器漂移的影响δp

测量时，A/D对积分器输出实时采样，得到积分器在固定时间间隔内的变化，再由单片机计算出合适的D/A值反馈到运算放大器的输入端，以补偿引起漂移的偏置电压。通过实验，将磁通计调至稳定后开始计时，3min内记录积分器的漂移，其变化量均在0.010%以内。如果将测量过程控制在3min以内，并进行漂移修正，则积分器漂移的影响urel(δp)可小于0.010%。

2.2.5 磁场均匀区的影响δS

电磁铁的校准报告表明，在以电磁铁极头中心为原点，半径为10mm的区域内，磁场不均匀性不超过0.019%。校准时规定试样的最大直径为18mm，并对样品进行多次测量，取其平均值，可以控制磁场不均匀性所带来的影响urel(δS)小于0.019%。

2.2.6 H通道磁通计分辨力的影响δf

2.2.7 试样端面与极头之间气隙的影响δg

气隙的影响可以表达为[3]：ΔH/H=-(2gB)/(μ0LH)，其中，B、H为退磁曲线上给定点的磁通密度和磁场强度，L为试样长度，g为试样和极面间的气隙。

测试时要对试样有严格要求，即试样内部及外部不能有砂眼、缺口、裂纹或其他缺陷，端面应相互平行，其平行度不超过公差等级9级，端面垂直于轴线，垂直度不超过公差等级9级，表面粗糙度Ra≤1.6μm。最大气隙可视为g=1.6μm。对于高度为10mm的试样，ΔH/H=-2×1.6×10-3/10=-0.032%，因此，气隙带来的不确定度可认为是urel(δg)=0.032%。

2.2.8 退磁速度及J≠0、B≠0对HcJ的影响δv

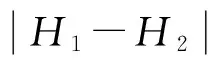
因此，偏离正常工作条件带来的不确定度为：

urel(δc) =[urel2(δK)+urel2(δp)+urel2(δS)+

urel2(δg)]1/2

=[(0.115%)2+(0.010%)2+

(0.019%)2+(0.032%)2]1/2=0.121%

2.2.9 测量重复性的影响δHc

2.3 矫顽力不确定度的合成及扩展不确定度

根据标准不确定度的合成公式[5]，得到内禀矫顽力HcJ的相对不确定度为：

urel2(δc)]1/2

=[(0.122%)2+(0.134%)2+

(0.200%)2+(0.121%)2]1/2

=0.30%

同样地，矫顽力HcB的相对不确定度为：

urel2(δc)]1/2

=[(0.231%)2+(0.134%)2+

(0.200%)2+(0.121%)2]1/2

=0.36%

取置信概率p=95%，k=2，则内禀矫顽力HcJ的扩展不确定度为：Urel(HcJ)=k×urel(HcJ)=2×0.30%=0.60%；矫顽力HcB的扩展不确定度为：Urel(HcB)=k×urel(HcB)=2×0.36%=0.72%。

3 结论

1)本文系统分析了测试NdFeB标样矫顽力过程中的影响因素，发现磁通计积分器的校准、探测线圈的校准、温度测量和测量重复性是对不确定度起主要贡献的方面。

2)通过不确定分析，当p=95%、k=2时，NdFeB圆柱标样的扩展不确定度分别为：Urel(HcJ)=0.60%，Urel(HcB)=0.72%。

3)通过本研究的分析，有利于指导测试人员和测量设备开发人员抓住影响测量结果的主要因素，进而改进测试操作过程，研发更精确、更稳定的信号探测手段。

[1] 胡伯平.稀土永磁材料的现状与发展趋势[J].磁性材料与器件，2014，45(2)

[2] 许志一，李小菊，龚文杰，等.铝镍钴永磁体磁参量的测量不确定度评估[J].计量技术，2015(3)

[3] GB/T 3217—2013,永磁(硬磁)材料磁性试验方法[S].

[4] Tumanski S.Handbook of Magnetic Measurements[M].CRC Press, 2011

[5] 叶德培.测量不确定度理解评定与应用[M].北京:中国质检出版社，2013

中国计量科学研究院基本科研业务费课题(35-ALC1514-15，35-AHY1323-13)

10.3969/j.issn.1000-0771.2015.11.06