基于进化博弈的水利工程施工安全监督管理

高 亚,章恒全

(河海大学商学院,江苏南京 211100)

基于进化博弈的水利工程施工安全监督管理

高 亚,章恒全

(河海大学商学院,江苏南京 211100)

为了探讨影响水利工程建设施工安全监督管理行为的因素,分析施工监督管理进化稳定策略,在水利工程建设监理单位和施工承包商具有有限理性的前提下,运用博弈论方法,构建了基于进化博弈的水利工程建设监理单位和施工承包商的博弈模型。对进化博弈稳定策略的分析结果表明:水利工程建设监理单位对水利工程建设施工安全监督管理的策略选择主要和严格监督管理成本与奖励、监督管理失误率、监督管理可能受到的惩罚等有关;施工承包商对水利工程严格施工的策略选择主要和严格施工成本与奖励、不严格施工可能受到的惩罚等有关;水利工程建设监理单位和施工承包商之间的进化博弈稳定策略与各影响因素的初始值有关。最后运用Matlab软件进行数值仿真,模拟博弈双方之间的动态博弈过程,并提出加强我国水利工程建设施工过程中安全监督管理的建议。

水利工程;施工安全监督管理;进化博弈;进化稳定策略

一般而言,与房屋建筑工程相比,水利工程规模庞大,施工技术复杂,工期长,且建成后需要定期维护,保证工程正常运行。水利工程一般修建在地形比较特殊的地方,如靠山修建,加大了施工的难度。同时,水利工程建筑物构造比较特殊,需要专业施工技术人员,施工技术难度加大了水利工程施工事故发生的风险性。

在水利工程建设过程中,施工总承包商往往会按专业、作业空间分布等方式将工程“合理”分包,以此达到工程质量、进度和投资的综合效益最大化[1]。施工总承包商在对工程进行分包及施工过程中,总承包商及分包商的行为都会影响业主的利益,因此业主会选择专业的监理单位对施工总承包商的行为进行监督,以减少自己的损失。Guanselaran等[2]认为施工总承包商和分包商是相互独立和理性的个体,每个个体受自身利益最大化的驱使,会选择实现局部最优。施工承包商和监理单位作为理性的个体,往往也会选择对自身利益有利的行为。施工总承包商在施工过程中,为追求自身利益最大化,有可能牺牲业主的利益,选择分包商及施工时不按水利工程施工标准进行。由于水利工程施工的特殊性,尤其是隐蔽工程的事后检查难度很大,监理单位在监督过程中可能会选择严格监督检查,保证不出现不良工程;但监理单位若追求自身利益最大化,也有可能选择与承包商“合作”。

相关学者对水利工程施工质量控制方面进行了研究。王国强等[3]构建监理单位和施工承包商之间的博弈模型,分析水利工程施工阶段质量控制的对策选择。王旭华等[4]构建承包商、监理和业主三方博弈模型,分析三方在水利工程质量管理方面的对策选择问题。王贺瑶等[5]构建业主和监理单位的委托代理模型,分析两者策略选择问题。关于水利工程建设安全监督管理的博弈问题研究主要集中在建筑业,如申玲等[6]根据建筑工程承包商和政府之间的博弈关系,构建双方的博弈监督管理模型。同时,进化博弈方法被广泛应用于其他工程,如刘德海等[7]将进化博弈应用于煤炭工业,构建煤炭工业和政府监督管理机构之间的进化博弈模型,分析博弈双方的初始影响因素等。

综上所述,对水利工程建设中相关利益主体的博弈分析相对较多,但研究中很少有运用进化博弈分析水利工程建设监理单位和施工承包商之间的博弈问题,尤其是两者之间的安全监督与安全施工的博弈问题。水利工程建设施工过程中最直接的利益主体就是业主、施工承包商和建设监理单位,但与施工安全事故有直接联系的是建设监理单位和施工承包商。本文根据相关资料,以水利工程建设监理单位和施工承包商为博弈主体,构建进化博弈模型,分析水利工程施工安全方面的博弈问题。

1 水利工程建设施工安全监督管理进化博弈模型构建

1.1 模型假设

1.1.1 博弈方假设

由于水利工程建设施工安全监督管理涉及的相关利益主体较多,本文考虑的博弈主体为水利工程建设监理单位和施工承包商。假设博弈双方为有限理性行为人,且双方没有发生“共谋”,监理单位不会接受施工承包商的贿赂,双方不发生寻租问题等。

1.1.2 策略假设

在博弈方有限理性的前提下,水利工程建设监理单位和施工承包商追求利益最大化。将博弈双方的策略抽象为具体行为。假设水利工程建设监理单位的策略集为:A1={严格监督管理,不监督管理},施工承包商的策略集为:A2={严格施工,不严格施工}。

1.1.3 得益假设

博弈方追求的最终目标及行为选择和判断的主要依据是博弈的最终结果,即博弈的得益[8]。本文对水利工程建设监理单位和施工承包商博弈双方的得益假设如下。

a.建设监理单位的得益假设:建设监理单位正常收入为I1,严格监督管理施工承包商施工过程的成本为C1;当施工承包商不严格施工时,建设监理单位在严格监督管理过程中会有一定的失误率e,即当施工承包商不严格施工且建设监理单位监督管理不到位时,建设监理单位受到一定的惩罚(直接经济损失等)F1;当施工承包商不严格施工且被建设监理单位发现时,建设监理单位得到一定的奖励(直接经济奖励等)R1。

b.施工承包商的得益假设:施工承包商的正常经营收入为I2,严格施工时的投入成本为C2,且在建设监理单位监督管理时,若其严格施工且无事故发生,会得到一定的奖励(直接的经济奖励等)R2;若承包商不严格施工,被建设监理单位发现时,不管是否发生安全事故,惩罚F2(直接经济惩罚等)。假设施工承包商严格施工就不会发生安全事故。

1.1.4 博弈过程

本文的博弈分析框架为两个有差别的有限理性博弈方群体,相互之间随机配对进行博弈,且博弈双方得益不对称,即基于进化博弈的非对称博弈分析。

1.2 模型构建

根据上述假设,得到水利工程建设监理单位和施工承包商的得益矩阵(见表1)。

表1 2×2非对称博弈得益矩阵

假设博弈方1所在位置的博弈群体中,博弈方1采取“严格监督管理”策略的比例为x,那么采取“不监督管理”策略的比例为1-x;假设博弈方2所在位置的博弈群体中,采取“严格施工”策略的比例为y,那么采取“不严格施工”策略的比例为1-y。

建设监理单位严格监督管理的期望得益为

建设监理单位不监督管理的期望得益为

建设监理单位的平均期望得益为

建设监理单位采取“严格监督管理”策略的复制动态方程为

同理可得:施工承包商采取“严格施工”策略的复制动态方程为

2 水利工程建设施工安全监督管理进化博弈模型分析

2.1 建设监理单位策略进化稳定分析

一般情况下,假设C1＜I1,R1＜F1,e很小。

图1时的复制动态相位

对F(x)求一阶倒数得

根据微分方程的“稳定性定理”可知:若F(x)的两个稳定状态为进化稳定策略,则F忆(x)＜0。所以x2=1为进化稳定策略(ESS)(见图2)。

图2时的复制动态相位

该博弈的雅克比矩阵为

该博弈系统雅克比矩阵的行列式和迹分别为

图3时的复制动态相位

2.2 施工承包商策略进化稳定分析

一般情况下,假设C2＜I2,R2＜F2。

2.3 博弈双方联合策略进化稳定分析

将博弈双方复制动态方程的微分方程联立求得本博弈的5个均衡点,见表2。

表2 各均衡点的稳定性分析结果

由微分方程表示的系统的均衡点不一定是系统的稳定点,即均衡点未必是稳定点,均衡点的最终稳定性状态可通过雅克比矩阵判断。

本文假设R1＜R2,C1＜C2,F1＜F2,R1＞C1,F1＞C1,R2＞C2,F2＞C2。

由表2可知,在上述假设条件下,水利工程建设监理单位与施工承包商博弈的进化稳定策略有3个,即:x1=0,y1=0;x1=0,y1=1和x2=1,y2=0。策略选择分别为:水利工程建设监理单位采取“不监督管理”策略,施工承包商采取“不严格施工”策略;水利工程建设监理单位采取“不监督管理”策略,施工承包商采取“严格施工”策略;水利工程建设监理单位采取“严格监督管理”策略,施工承包商采取“不严格施工”策略。以上所得出的博弈双方采取的策略主要是根据不同的初始值情况所采取的,初始值改变时,双方采取的策略会随之改变。

3 数值仿真

为了更清楚地解释水利工程建设监理单位和施工承包商之间进化博弈的演变过程,本文对影响水利工程建设监理单位和施工承包商的策略选择的因素指标进行赋值,并运用Matlab7.0[9]软件进行数值仿真,模拟进化博弈演变过程。

令e=0.2,R1=5,R2=7,C1=3,C2=4,F1=4,F2=5,将各值代入式(4)和(5)中得

a.建设监理单位选择“严格监督管理”策略比例分别取x=0.7和x=0.3。

绘制施工承包商在不同初始比例的“严格施工”策略下的动态博弈过程(见图4)。

图4 施工承包商策略选择随博弈时间变动的演化过程

由图4(a)可知,当建设监理单位策略选择x＞0.5时,在不同的初始“严格施工”策略比例下,施工承包商选择“严格施工”的比例都会收敛到1,即施工承包商最终会选择“严格施工”策略。

由图4(b)可知,当建设监理单位策略选择比例x＜0.5时,在不同的初始“严格施工”策略比例下,施工承包商选择“严格施工”的比例都会收敛到0,即施工承包商最终会选择“不严格施工”策略。

b.施工承包商选择“严格施工”策略比例分别取y=0.7和y=0.3。绘制建设监理单位在不同比例的“严格监督管理”策略下的动态博弈过程(见图5)。

图5 建设监理单位策略选择随博弈时间变动的演化过程

由图5(a)可知,当施工承包商策略选择y＞0.5时,在不同的初始“严格监督管理”策略比例下,建设监理单位选择“严格监督管理”的比例都会收敛到0,即建设监理单位最终会选择“不监督管理”策略。

由图5(b)可知,当施工承包商策略选择比例y＜0.5时,在不同的初始“严格监督管理”策略比例下,建设监理单位选择“严格监督管理”的比例都会收敛到1,即建设监理单位最终会选择“严格监督管理”策略。

c.绘制水利工程建设监理单位和施工承包商之间的进化博弈动态过程,见图6。

由图6可知,水利工程建设监理单位和施工承包商之间的进化博弈一直处于动态过程,博弈双方都会根据对方的策略选择动态地改变自己的策略选择。

图6 博弈双方进化博弈动态过程

4 结 语

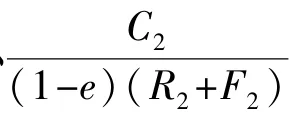
[1]郜军艳,聂相田,王博.水利工程建设施工供应链质量控制博弈研究[J].水电能源科学,2012,30(9):115-118

[2]GUANSELARAN A,PATER C,MCGAUGHEY R E.A framework for supply chain performance measurement[J]. International Journal of Production Economics,2004,87 (3):333-347.

[3]王国强,周书杰,李鹏,等.基于博弈论的监理人水利工程施工阶段质量控制[J].水利经济,2010,28(2):59-61.

[4]王旭华,张春华,王南江.水利工程建设质量管理的博弈研究[J].治淮,2012(5):42-44.

[5]王贺瑶,姜国辉,佟国红,等.水利工程中的业主和监理之间的委托代理博弈模型[J].安徽农业科学,2007,35 (3):920-921.

[6]申玲,孙其珩,吴立石.基于博弈关系的建筑安全投入监管对策研究[J].中国安全科学学报,2010,20(7):110-115.

[7]LIU Dehai,XIAO Xingzhi,LI Hongyi.Historical evolution and benefit-costexplanation of periodical fluctuation in coal mine safety supervision:An evolutionary game analysis framework[J].European Journal of Operational Research, 2015,243(3):974-984.

[8]谢识予.经济博弈论[M].3版.上海:复旦大学出版社, 2013.

[9]徐金明.MATLAB实用教程[M].北京:清华大学出版社,北京交通大学出版社,2005.

TV523

A

1003 -9511(2015)04 -0072 -05

2015-04 -13 编辑:胡新宇)

10.3880/j.issn.1003 -9511.2015.04.018

高亚(1991—),女,江苏宿迁人,硕士研究生,主要从事管理科学与工程研究。E-mail:1584091323@qq.com