中硬场地下两种土层地震反应方法与精确解的对比①

李瑞山， 袁晓铭， 李程程

(中国地震局工程力学研究所地震工程与工程振动重点实验室，黑龙江 哈尔滨 150080)

中硬场地下两种土层地震反应方法与精确解的对比①

李瑞山， 袁晓铭， 李程程

(中国地震局工程力学研究所地震工程与工程振动重点实验室，黑龙江 哈尔滨 150080)

基于谐波入射下的波动理论频域精确解，导出线性时域精确解，并在Matlab环境中编制相应的计算程序；选取8个简化的中硬场地剖面，用LSSRLI-1、精确解和SHAKE2000三种方法计算各场地在不同输入条件下的地震反应。结果表明：程序计算所得地表反应谱和土体剪应变分布与SHAKE2000结果一致；LSSRLI-1方法得到的地表反应谱与前二者结果一致；LSSRLI-1方法在某些情况下得到的土体剪应变分布与另外二者结果存在较大偏差，该偏差对地表反应谱有着不可忽略甚至非常显著的影响。

地震反应分析； LSSRLI-1； 精确解； 土表反应谱； 土体剪应变

0 引言

土层地震反应分析是岩土地震工程领域的一个重要分支，主要研究场地对土体中传播的地震波的影响。土层场地在承载上部结构的同时还要充当地震波由基岩向地表传播的媒介。建筑结构在地震作用下的响应分析需要以地面运动作为输入，所以地表运动预测的精度直接关系到结构地震反应分析的可靠性。土层结构对地表加速度峰值、反应谱平台值和特征周期都有直接的影响[1-3]，通过土层地震反应分析得到的土体剪应变分布以及地表运动特征可以从一定程度上预测场地在地震作用下液化的可能性[4]。

现有的土层地震反应分析方法主要可以分成线性、等效线性和非线性三类。土体在动剪应力作用下往往表现出强烈的应力-应变非线性关系，鉴于此，线性方法在实际分析当中很少被使用。非线性方法需要在时域当中通过微小的时间步积分来得到相应的分析结果，所以在实际操作中非常耗时。不仅如此，非线性方法的分析精度在很大程度上依赖于土体动应力-动应变本构关系的正确与否，而土体动力本构本身就非常复杂。等效线性化方法利用线性方法，数学概念简单，物理意义明确，并将土体动力非线性性质引入到了分析当中，在不背离其本质的前提下大大方便了计算。等效线性化方法在总体动力学效应大致相当的意义上用一个等效的剪切模量和阻尼比代替所有不同应变振幅下的剪切模量和阻尼比，将非线性问题转化为线性问题[5]。自Seed和Idriss于1970年首次将等效线性化的概念引入岩土地震工程领域，并于1972年编制了相应的计算程序——SHAKE[6]，现在SHAKE版本已更新至SHAKE2000，是国际主流的土层反应分析等效线性化计算程序。目前我国地震安全评价所使用的是LSSRLI-1程序[7-8]，该程序自提出至今已有20多年，代表着当时的国际先进水平，为我国的防震减灾事业做出了卓越的贡献。但是，在实际使用过程当中该程序也表现出了一些缺点和不足[9]，尤其是当土层较软或输入地震运动较强时，其计算结果不合理性较为明显。

本文拟复现一维土层地震反应分析频域精确解，并利用快速傅里叶变换(FFT)和逆傅里叶变换(IFFT)实现幅值和频率成分都极不规则的随机地震荷载在时域和频域当中的相互转换。基于以上理论，结合傅里叶变换的线性可叠加性，给出土层地震反应分析一维线性精确解，并在Matlab环境中编制相应的计算程序。最后利用该程序进行中硬场地在不同输入条件下的地震反应计算，并将所得结果与SHAKE2000和LSSRLI-1进行对比。为了和本文的线性精确解保持一致性和可对比性，SHAKE2000和LSSRLI-1在计算时均采用线性不迭代方式。

1 线性精确解

假设实际场地水平成层，土性为各向同性的Kelvin-Voigt黏弹性体，输入的地震运动为由基岩垂直向上入射的剪切波。各土层由其层厚h、重度ρ、初始剪切模量G、初始阻尼比ξ来表征，如图1所示。各层的局部坐标原点位于层顶，方向向下。土体中的波动用数学方程可以表达为：

(1)

在频率为ω的谐波入射下，式(1)的解为：

图1 水平成层简化模型Fig.1 Simplified model of the horizontally layered site

(2)

具体对第n层土，以其空间坐标zn和时间坐标t所表达的位移函数为：

(3)

式中，E和F分别为土层中所传播的上行波和下行波波幅，k为波数，其表达式为：

(4)

根据分层界面上位移和应力的连续条件，可以导出相邻两层波幅之间的数量关系：

(5)

用矩阵可以简单表达为：

(6)

根据输入，通过递归便可得到各层的波幅矢量。然后根据位移场表达式(3)和几何方程，可以求得土层中剪应变表达式为：

(7)

根据先前求得的各层波幅矢量便可很容易得到土体当中剪应变的分布。另外，为了考虑土体等效阻尼，采用复刚度G*代替原来的剪切刚度G，剪切波速υS和波数k随之相应变化，不再赘述。

(8)

基岩输入的剪切波经快速傅里叶变换可以分解为一系列谐波的叠加，将各自分别输入所得到的响应量对应叠加后进行逆傅里叶变换便可得到相应的时域反应。

本文根据上述理论推导，在Matlab环境当中编制相应的计算程序，用来求解基岩输入加速度时程时的地表响应和土体剪应变分布。为了更加直观地反应输入参数相同时输出量的差异性，计算采取线性运算，不进行迭代。

2 计算模型

本文采用单层土和双层土两种简化计算模型，共计8个计算剖面，其中4个单层剖面，4个双层剖面，各剖面的土层参数详见表1，其中υS1和υS2分别为上下两层土的剪切波速，h1和h2分别为上下两层厚度。为分析输入地震动频谱成分对计算结果差异性的影响，选取三条频谱特性各异的地震动时程作为输入，分别为ElCentro波、AKTH19波和KSRH09波，其中AKTH19波和KSRH09波是从KiK-net数据库中选取的井下台站实测数据。AKTH19波的主要频谱特点是低频成分绝对占优，高频分量很少，而KSRH09波相比而言具有十分丰富的高频成分。计算时分别将三条加速度时程调幅至0.1g、0.2g和0.4g作为输入，以对比三种方法计算结果差异性与输入地震动强烈程度之间的关系。调幅至0.2g时的加速度时程曲线如图2所示。

图2 输入加速度时程曲线Fig.2 Input acceleration time histories

在采用等效线性化计算时，某次循环所使用的动力非线性参数是根据上一次循环所得到的土体剪应变分布而定的，等效剪应变一般可按下式计算：

(9)

其中，γmax为剪应变时程的幅值。按式(9)算得等效剪应变之后，便可从模量比和阻尼比随剪应变变化曲线上插值得到新的G/Gmax和ξ值进行下一次迭代计算，直到相邻两次计算结果相对差值小于某一容许值。

土层地震反应分析结果能够为工程实际所直接应用的是地表运动响应，包括运动幅值及其反应谱等。地表运动与土地剪应变分布有着密切的关系。为了直观表现剪应变差异对地表加速度反应谱的影响，本文将用线性方法得到的剪应变按等效线性化的思想插值后求得新的动力非线性参数，并利用新参数重新计算地表响应。这样剪应变的差别便通过重新计算的地表反应谱差别表现出来。文中插值所用的是孙锐等[10]通过大量共振柱试验统计得出的粉质黏土非线性平均线，具体见图3。

图3 剪切模量和阻尼比随剪应变幅的变化曲线Fig.3 Variation of shear modulus and damping ratio with shear strain amplitude

表1 计算模型参数表

Table1 Parameters of the calculation models

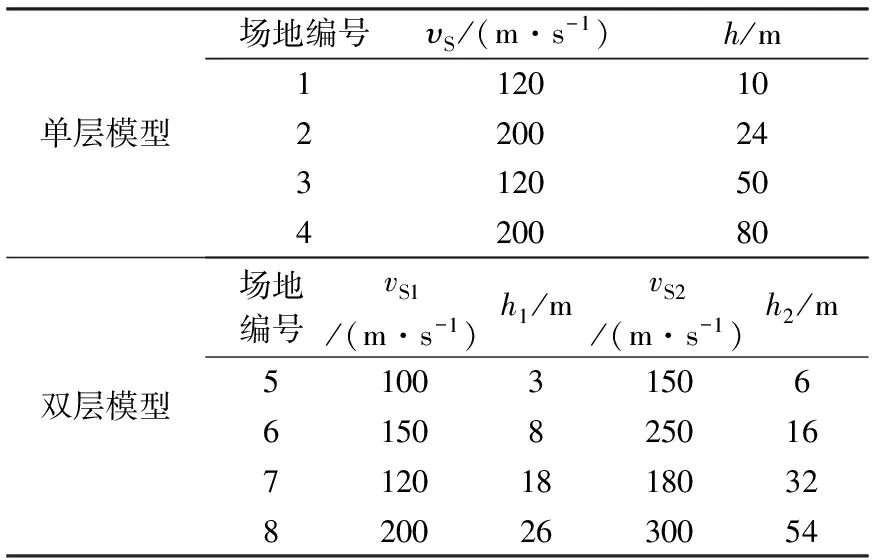
单层模型场地编号υS/(m·s-1)h/m112010220024312050420080双层模型场地编号vS1/(m·s-1)h1/mvS2/(m·s-1)h2/m51003150661508250167120181803282002630054

3 结果对比分析

土层地震反应分析所得到的地表加速度反应谱可以为工程实际所直接应用，其计算的正确与否直接关系到对应的计算方法的可靠性。本文共选取72种计算工况，但因为采取不迭代的计算方式，实际独立的工况只有24种。限于篇幅，图4中仅绘制了在输入波峰值为0.2 g时其中8个工况所计算得到的地表加速度反应谱。从图中可以清晰看出由精确解、SHAKE2000和LSSRLI-1三种方法计算得到的地表加速度反应谱几乎完全相同，这充分说明LSSRLI-1计算地表加速度的方法是可靠的，同时也说明本文在Matlab环境当中编制的精确解程序在输入参数相同的情况下所计算出的地表运动同国际主流的SHAKE2000结果是一致的。

图4(c)、(e)和(g)工况的输入幅值均为0.2 g的KSRH09波，得到的地表加速度反应谱从峰值个数和大体形状上来讲很相似，但很明显峰值大小和相对应的周期各不相同，这充分体现了场地条件对输入加速度波的频谱特性的改变，不同场地在相同输入下的响应不尽相同。从图4(b)、(d)和(f)三个工况对比可以得到相同的结论。另外，从图4中还可以看出，在不同的基岩输入下得到的地表反应谱相互之间存在很大的差异性，这说明地表输出同时受到基岩输入和场地条件的影响。

图5是土体剪应变随深度的分布，其中输入波峰值为0.2 g，本文选取24个独立计算工况中的8个作为代表来呈现。从图中可以看出，本文编制的精确解程序计算得到的土体剪应变分布与SHAKE2000结果非常吻合，这种一致性与场地和输入条件均无关，说明SHAKE2000剪应变计算结果完全可以由本文程序来代表。综合上面三种方法计算得到的地表反应谱的一致性可以得出结论：SHAKE2000计算出的土体剪应变和地表反应谱同本文根据精确解所编制程序的计算结果均一致，本文程序与国际主流的SHAKE2000具有相同的精度。下文中SHAKE2000结果均由精确解来代表，而不再单独进行对比分析。

从图5中可以明显看出LSSRLI-1程序计算出的土体剪应变分布与精确解结果存在一定差异。图5(d)和(f)两工况当中剪应变的差别很小，图5(a)、(b)和(e)三个工况呈现出不可忽略的剪应变差别，剩下的图5(c)、(g)和(h)三个工况的剪应变差异性十分显著，并且均为LSSRLI-1结果远大于精确解结果。下面就影响剪应变相对差别大小的不同因素进行分析。

首先，整体剪应变水平的大小直接影响着二者剪应变差异性的大小。为此将图示8个工况分为三组，图5(e)和(f)为低应变组，该组呈现出的剪应变之间有一定的差异性，但并不显著，尤其对于分层模型中的上层，三种方法得到的剪应变几乎完全一致；图5(a)，(b)和(h)为中应变组，该组剪应变差别较低应变组明显有所增大，甚至如图5(h)所示非常显著；图5(c)，(d)和(g)为大应变组，剪应变差别也更为明显。一般地，剪应变水平越高时，LSSRLI-1计算得到的土体剪应变分布与精确解偏差越显著。

图4 地表加速度反应谱(输入波峰值=0.2 g)Fig.4 Ground acceleration response spectrum (peak acceleration=0.2 g)

图5 土体剪应变分布(输入波峰值=0.2 g)Fig.5 Distribution of soil shear strains (peak acceleration=0.2 g)

另外，输入波的频谱特性对二者计算得到的土体剪应变差别也有很大的影响。三条输入波中，按高频成分多少依次为AKTH19、El Centro和KSRH09。在AKTH19波输入时(图5(b)、(d)和(f)，LSSRLI-1所得剪应变在一定程度上较精确解结果偏大或偏小，但偏差不十分显著。当高频成分相对较多的El Centro输入时，LSSRLI-1剪应变较精确解结果均偏大，有时偏差甚至非常显著。将三条波中高频成分最多的KSRH09波作为输入波时，LSSRLI-1剪应变比精确解结果严重偏大，二者相对差值很多时候超过100%。由此可见，LSSRLI-1剪应变计算的适用性与输入波有很大关系，低频成分较丰富的波输入时，计算结果偏差较小，计算方法适用性较强；高频成分丰富的波输入时，计算所得剪应变偏差较为显著，计算方法适用性较差。

但是剪应变不能直接被工程实际所使用，通过其差异性无法依据工程可接受标准直观地判断某种计算方法应用于土层地震反应分析时是否可靠。为了用剪应变差别来影射其对地表反应谱的影响，本文利用图5中所示的剪应变，按式(9)算得各层的等效剪应变，然后按非线性曲线(图3)插值得到新的土层参数，重新计算得到地表加速度反应谱(图6)。因图5中的SHAKE2000结果和精确解结果几乎相同，所以在图6中没有绘出SHAKE2000结果。

图6 使用新参数计算出的地表加速度反应谱Fig.6 Ground acceleration response sprctrum calculated by using the updated parameters

结合图5，从图6中可以明显看出，中硬场地剪应变计算结果偏差越大，对地表反应谱的影响就越明显。图5中(a)、(b)、(d)、(e)和(f)所示的剪应变差别对地表反应谱有一定影响，但影响不大，在工程可接受范围之内。图5中(e)、(g)和(h)三个工况所表现出的剪应变偏差十分显著，对应在图6中表现出十分显著的地表反应谱差别。另外图5中(a)、(b)剪应变差别明显大于图5(d)，而图6并未表现出(a)、(b)工况差别明显大于(d)工况的现象，究其原因是因为(d)工况的剪应变水平较(a)、(b)两工况要高很多，不同的应变水平对非线性的敏感程度不同。综合上述两点可以得出如下结论：剪应变差别对地表反应谱的影响同时受偏差大小和应变整体水平两个因素控制，但其中剪应变差别占主导。

4 结论

本文复现了谐波输入下的土层反应频域精确解，在此基础上导出了时域线性精确解，并在Matlab环境中编制了相应的计算程序。文中共选取了8个简化的中硬场地剖面，选取了三条频谱特性各异的加速度时程作为输入。经对比分析由精确解、SHAKE2000和LSSRLI-1分别计算出的土表加速度反应谱和土体剪应变分布，可以得出如下结论：

(1) 本文根据导出的精确解所编制的计算程序具有与SHAKE2000所代表的国际主流等效线性化土层地震反应分析方法同样的精度，二者计算得到的土表加速度反应谱和土体剪应变分布完全一致。

(2) LSSRLI-1计算得到的土表加速度反应谱与精确解和SHAKE2000结果一致，LSSRLI-1计算地表运动的相应模块是可靠的。

(3) LSSRLI-1计算所得剪应变与精确解结果之间存在一定的偏差，但大部分情况下偏差很小，由此导致的地表反应谱偏差在工程可接受范围之内。

(4) 当输入波高频成分较丰富时，LSSRLI-1计算所得剪应变可能会出现较为显著的偏差，对地表反应谱影响十分明显，不可忽略，说明该方法对部分情况有一定的不适用性，剪应变的计算方法亟需改进。

References)

[1] 薄景山，李秀领，刘德东，等.土层结构对反应谱平台值的影响[J].地震工程与工程振动，2003，23(4)：29-33.BO Jing-shan，LI Xiu-ling，LIU De-dong，et al.Effects of Soil Layer Construction on Platform Value of Response Spectra[J].Earthquake Engineering and Engineering Vibration，2003，23(4)：29-33.(in Chinese)

[2] 薄景山，李秀领，刘德东，等.土层结构对反应谱特征周期的影响[J].地震工程与工程振动，2003，23(5)：42-45.BO Jing-shan，LI Xiu-ling，LIU De-dong，et al.Effects of Soil Layer Construction on Characteristic Periods of Response Spectra[J].Earthquake Engineering and Engineering Vibration， 2003，23(5)：42-45.(in Chinese)[3] 薄景山，李秀领，刘红帅.土层结构对地表加速度峰值的影响[J].地震工程与工程振动，2003，23(3)：35-40.BO Jing-shan，LI Xiu-ling，LIU Hong-shuai.Effects of Soil Layer Construction on Peak Accelerations of Ground Motions [J].Earthquake Engineering and Engineering Vibration，2003，23(3)：35-40.(in Chinese)

[4] 孙锐，袁晓铭.液化土层地震动特征分析[J].岩土工程学报，2004，26(5)：684-690.SUN Rui，YUAN Xiao-ming.Analysis on Featrue of Surface Ground Motion for Liquefied Soil Layer[J].Chinese Journal of Geotechnical Engineering，2004，26(5)：684-690.(in Chinese)

[5] 廖振鹏.工程波动理论导论[M].北京：科学出版社，2002.LIAO Zhen-peng.Introduction to Wave Motion Theory for Engineering[M].Beijing：Science Press，2002.(in Chinese)

[6] Shnabel P，Lysmer J，Seed H B.SHAKE：A Computer Program for Earthquake Response Analysis of Horizontal Layer Sites[R].1972.

[7] 廖振鹏，李小军.地表土层地震反应的等效线性化解法[M]//廖振鹏.地震小区划(理论与实践).北京：地震出版社，1989：141-153.LIAO Zhen-peng，LI Xiao-jun.Linearization Method for Computing Earthquake Response of Ground Layered Soil[M]//LIAO Zhenpeng.Seismic Microzonation.Beijing：Seismological Press，1989，：141-153.(in Chinese)

[8] 李小军.一维土层地震反应线性化计算程序[M]//廖振鹏，地震小区划(理论与实践)北京：地震出版社，1989：250-265.LI Xiao-jun.A Computer Program for Calculating Earthquake Response of Ground Layered Soil[M]//Liao Zhen-peng.Seismic Microzonation.Beijing：Seismological Press，1989：250-265.(in Chinese)

[9] 刘德东，齐文浩，张宇东，等.现行土层地震反应分析存在的问题[J].防灾科技学院学报，2009，21(3)：34-37.LIU De-dong，QI Wen-hao，Zhang Yudong，et al.Problems Existing in Current Seismic Response Analysis for Soil Layers[J].J of Institute of Disaster-Prevention Science and Technology，2009，11(3)：34-37.(in Chinese)

[10] 孙锐，陈红娟，袁晓铭.土的非线性动剪切模量比和阻尼比不确定性分析[J].岩土工程学报，2010，32(8)：1228-1235.SUN Rui，CHEN Hong-juan，YUAN Xiao-ming.Uncertainty of Non-linear Dynamic Shear Modular Ratio and Damping Ratio of Soils[J].Chinese Journal of Geotechnical Engineering，2010，32(8)：1228-1235.(in Chinese)

Contrasting Study of Two Seismic Response Methods and the Exact Solutions for Moderately Stiff Soil Sites

LI Rui-shan， YUAN Xiao-ming， LI Chieng-cheng

(KeyLaboratoryofEarthquakeEngineeringandEngineeringVibration，InstituteofEngineeringMechanics，ChinaEarthquakeAdministration，Harbin，Heilongjiang100080，China)

Earthquake ground motions can significantly affect buildings when they are amplified in surface soil layers.Therefore，in order to estimate the behavior of buildings during severe earthquakes，it is essential to evaluate those characteristics of amplification.Although investigations have been carried out，many problems remain unsolved with regard to those characteristics.Ground response analysis typically involves predictions of surface ground motions，developing a spectrum of design responses，determining dynamic stress and strain，and evaluating the potential for liquefaction.Methods used to calculate the ground response are commonly divided into linear，nonlinear，and equivalent linear concepts.The linear analysis assumes that the shear modulus as constant.However，soils often exhibit nonlinear behavior，even at low levels of strain.The nonlinear method is time consuming.The equivalent linear method，represented by the SHAKE model，is one of the most frequently used methods for analysis of ground responses to earthquakes.This method is used primarily for approximations because it uses effective strain to define the material property for analysis.However，the equivalent linear method remains the most popular method of seismic response analysis.It has been 20 years since the safety evaluation program LSSRLI-1 was developed and was used for seismic response analysis.At the time，LSSRLI-1 represented the most advanced method and contributed greatly to earthquake preparedness and disaster reduction for China.However，some deficiencies in the model were identified.Based on its focus in the frequency domain with a harmonic wave incident，the exact linear solution was deduced in the time domain，and compiled into a program in the Matlab environment.For the study，eight sites with medium-hard soils were chosen.Seismic responses were calculated using three different methods：the LSSRLI-1，exact solution，and SHAKE2000.The results show that the ground response spectrums and distribution of soil shear strain，calculated using the exact solution and SHAKE2000 methods，are in agreement with each other.The ground response spectrums，calculated using LSSRLI-1，were consistent with the other two methods.However，in some cases，the distribution of soil shear strain，calculated using LSSRLI-1，showed a relatively large deviation from the SHAKE2000 and exact solution methods.The extent of these differences may significantly affect the estimates of ground motion，and cannot be ignored.

seismic response analysis； LSSRLI-1； exact solution； response spectrum of soil surface； soil shear strain

2014-08-20

国家科技部地震行业专项(201308015)；黑龙江省自然科学基金资助项目留学归国基金(LC2013C14)；国家自然科学基金(51278472)

李瑞山(1987-)，男，博士研究生，主要从事土动力学和岩土地震工程研究.E-mail：lrshan22@hotmail.com

TU43

A

1000-0844(2015)02-0565-06

10.3969/j.issn.1000-0844.2015.02.0565