MPA方法在不同高度桥墩地震响应分析中的适用性研究①

蒋崇文， 王典斌， 卢 皓

(1.湖南大学土木工程学院，湖南 长沙 410000； 2.中国中铁二院集团有限公司，四川 成都 610031；3.同济大学桥梁工程系，上海 200092))

MPA方法在不同高度桥墩地震响应分析中的适用性研究①

蒋崇文1， 王典斌2， 卢 皓3

(1.湖南大学土木工程学院，湖南 长沙 410000； 2.中国中铁二院集团有限公司，四川 成都 610031；3.同济大学桥梁工程系，上海 200092))

桥梁通常是线路中的控制工程，其抗震性能显得尤为重要。作为梁桥重要组成部分的桥墩，往往是地震作用下容易受到损伤的构件。结合西部山区梁桥的典型桥墩结构形式，基于纤维模型的有限元方法建立桥墩的非线性数值分析模型。采用MPA方法对不同高度桥墩的地震响应进行分析，以非线性时程分析方法的计算结果为基准研究MPA方法的适用性。计算表明MPA方法在分析高阶模态参与程度较高的高墩构件时适用性较差。

多模态的Pushover方法； 非线性时程分析方法； 纤维模型； 桥墩抗震分析

0 引言

随着西部地区交通建设事业的不断发展，跨越深谷、沟壑、江河的高墩桥梁日益增多。现行的《公路桥梁抗震细则》(JTG/TB02-01-2008)对墩高不超过40 m的规则桥梁提供了可靠的设计流程[1]，然而对于墩高超过40 m的桥梁则需要专门进行研究[2-5]。美国CALTRANS抗震设计规范也仅适用于规则桥梁，而高墩桥梁一般都是典型的非规则桥梁[6]。当墩身较高时墩身质量较大，高阶模态参与程度不可忽视，地震频谱特性对其抗震性能影响也会较大，此类桥墩的抗震性能及分析方法都有待进一步的详细研究，现在最常用的是非线性静力分析方法。

非线性静力分析方法由于操作简便、概念简单，在地震工程界已得到了广泛应用，但它的适用范围仍需要进一步探讨，尤其是对非规则结构。传统的Pushover方法的理论基础是建立在两个基本假定上的：(1)假定结构的地震响应主要由基阶模态控制；(2)结构沿高度的变形可由固定的形状向量表示，且在整个地震反应过程中结构的形状向量保持不变。为解决传统Pushover方法的局限性，A.K.Chopra等[7]在结构动力学的基础上提出了考虑高阶模态的MPA方法，该方法的提出是针对建筑结构的，在桥梁结构中的适用性还有待研究。本文将采用MPA方法分析不同高度桥墩的地震响应，并以非线性时程分析方法的计算结果为基准，对MPA方法的适用性予以讨论。

1 MPA方法

A.K.Chopra和R.K.Goel[7]提出了基于多模态的Pushover方法(简称为MPA方法)，该方法采用与结构各阶模态相应的加载模式对结构进行Pushover分析，以此将原结构转化为对应各阶模态的单自由度体系，并分别计算相应于各阶模态的地震响应，最后将各阶模态的地震响应进行组合得到结构总的地震响应。该方法的提出一开始是针对高层建筑结构的抗震分析，其理论基础可参见相关文献，这里不再冗述。下面介绍该方法计算梁桥地震响应的步骤，然后对MPA方法应用于高墩梁桥抗震分析中的适用性进行探讨。

采用MPA分析方法求解梁桥地震响应时，通常采用以下步骤：

(1) 计算出桥梁模型各主要模态φn，对多自由度体系进行模态分解，每一个模态对应一个单自由度体系，从而完成从多自由度体系向单自由度体系的转变。

(2) 对第n阶模态，采用mφn侧向荷载分布进行Pushover分析，完成了地震动力加载向静力加载的转变；求得墩底剪力总和-控制点位移(Vbn-urn)Pushover曲线，其中vbn为各桥墩墩底剪力之和，urn为主梁参考点的位移。

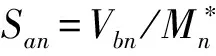
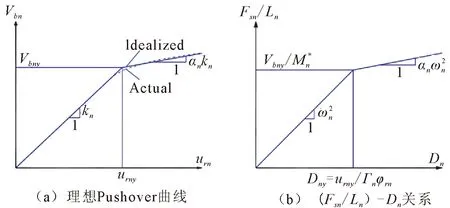
图1 Pushover曲线及格式转换[7]Fig.1 Pushover curve and the format conversion

(4) 求解第n阶模态对应的单自由度体系的地震位移需求Dn。在得到第n阶模态对应的能力谱曲线以后，可以采用非线性时程分析方法求解Dn(t)，也可以将能力谱曲线与需求谱曲线组合来求解Dn(t)的最大包络值Dmax n。

在得到桥梁结构的地震位移需求后，可采用模态Pushover分析方法得到各阶模态对应umax，n的峰值响应rn0(力、位移或墩身各截面曲率)，通过SRSS组合方式加以组合就能得到各阶模态总的反应峰值。

在基于模态的MPA方法的计算过程中，一般以结构顶点作为控制点，通过逐步增大侧向荷载fn0=ΓnmφnAn使结构的顶部位移达到预定的位移urn0，从而求得第n阶模态的地震响应峰值rn0。本文选择以桥墩墩顶作为加载控制点。

反应谱法和时程分析方法对规则结构在弹性阶段进行抗震分析具有一致性[8]，由于本文讨论的是强震作用下高墩桥梁进入塑性阶段后的地震抗震性能特点，因此采用非线性时程分析方法的计算结果作为基准来评估MPA方法的适用性。

2 纤维模型

为较准确地了解高墩桥梁在强震作用下的抗震性能，合理模拟钢筋混凝土墩柱非线性阶段的材料性能最为关键。本文采用Taucer等[9]提出的基于柔度法的弹塑性梁柱单元(分布塑性单元)，将钢筋和混凝土离散为纤维，假设纤维之间完全粘结，且满足平截面假定。

弹塑性纤维梁柱单元的非线性特性由纤维的非线性应力-应变关系(材料非线性)来表示，国外学者已提出了许多模拟混凝土和钢筋材料本构关系的计算模型，本文采用Mander模型[10]模拟混凝土应力-应变关系(图2(a))；钢筋采用Giuffré-Menegotto-Pinto模型[11](图2(b))。

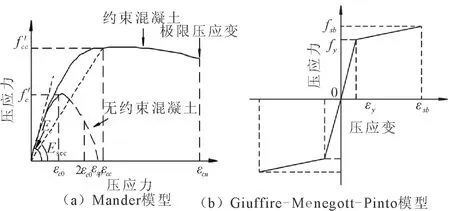
图2 材料本构模型Fig.2 Material constitutive model

本文采用OpenSees(Open System for Earthquake Engineering Simulation)程序完成有限元分析。该程序是加州大学Berkeley分校太平洋地震工程研究中心(PEER)开发的一个面向对象，能够建立结构体系计算模型，并进行非线性动力分析以及地震反应结果处理的结构分析系统。OpenSees的研发目标是为地震工程研究人员提供一个统一、开放的非线性动力仿真计算平台[12]。

3 桥墩计算模型的建立和地震动作用的选取

在建模时将高墩桥梁模型简化为单墩模型。单墩计算模型采用墩底固结的悬臂直梁，墩身质量堆聚在相应的节点上，将与桥墩相邻的一跨上部结构质量等效为凝聚在墩顶的集中质量，计算模型和截面形式见图3，各计算模型的基本参数见表1。

采用结构的初始刚度进行模态分析，得到30、60、90 m桥墩的模态(图4)。

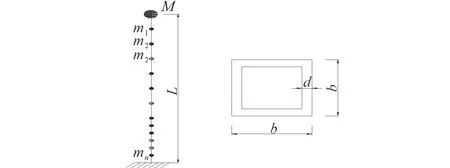
图3 桥墩计算模型及截面形式Fig.3 Calculation model and section of the pier

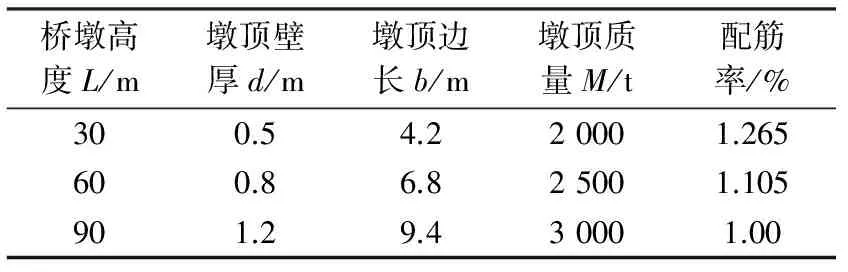
表1 桥墩基本参数

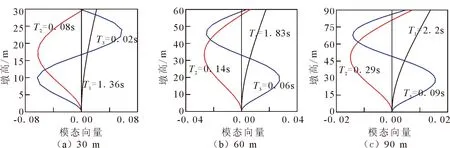
图4 不同墩高计算模型的初始模态向量Fig.4 Initial modal vector of the calculation model with different pier heights

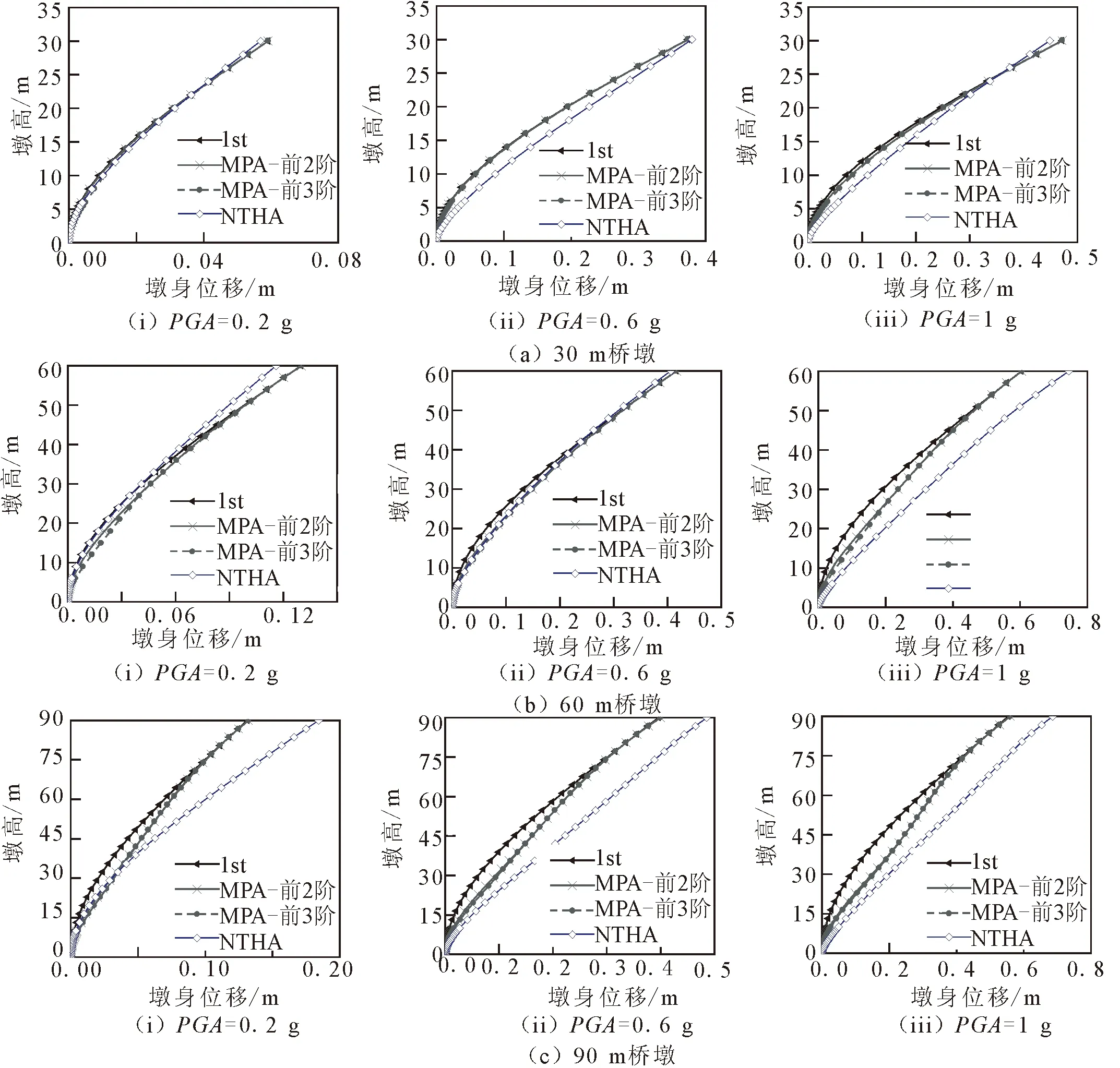
图5 各墩的墩身位移响应Fig.5 Pier body displacement response of each pier

对墩底纤维截面进行轴力-弯矩-曲率的分析，得到墩底截面的曲率分析结果(表2)。

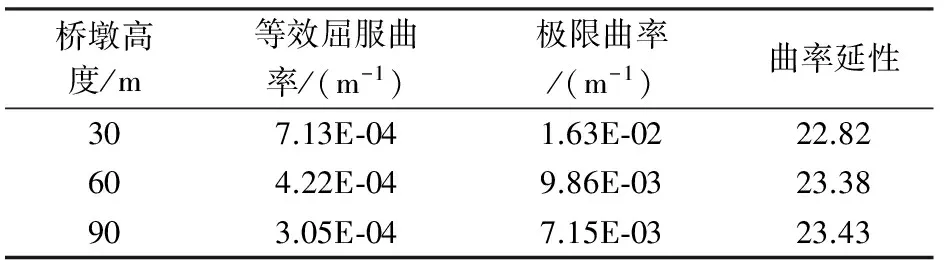
表2 墩底截面曲率分析结果

由于El-Centro波较为典型，本文采用这条波的N-S方向分量作为地震输入，对不同墩高的桥墩计算模型在高阶模态影响下的地震响应特点及抗震性能进行分析。

4 计算结果及分析

4.1 墩身位移地震响应峰值的计算及误差

采用MPA方法对不同墩高计算模型在El-Centro波地震作用下的位移响应峰值进行估计，并将结果列在图5中。其中分别列出考虑了一阶模态、前两阶模态和前三阶模态的计算结果，为了便于比较，将非线性时程分析(NTHA)方法的计算结果也列在图中。

将MPA方法的计算误差列在图6中。误差的定义为

(1)

式中：RPushover为Pushover方法计算的地震响应；RNTHA为NTHA方法计算的地震响应。本文后续研究提到的误差均采用式(1)的定义。

从图5和图6可知，用MPA方法在估计不同墩高计算模型的墩顶位移地震响应时，采用多模态和只考虑第一阶模态的计算结果差别并不大。可见墩顶位移地震响应的贡献基本来自于结构的一阶模态，高阶模态对墩顶位移地震响应的贡献程度很小。MPA方法估计各墩的墩顶位移地震响应的误差只在计算90 m高墩时较大，为30%。采用MPA方法估计墩身位移地震响应时墩身中下部误差较墩顶更大，且随着墩高和地震强度的增加，这种趋势将更加明显。除了该方法本身的局限性以外，计算时所采用的阻尼大小对非线性时程分析方法的结果也有一定的影响。

4.2 墩身截面曲率地震响应峰值的计算及误差

高墩最为直接的损伤控制指标为地震动作用下墩身各截面曲率的地震响应。这里将MPA方法估计不同墩高计算模型在El-Centro波地震作用下墩身各截面曲率地震响应峰值列在图7中，分别列出考虑了一阶模态、前两阶模态和前三阶模态的计算结果。为了便于比较，将非线性时程分析(NTHA)方法的计算结果也列在图7中。

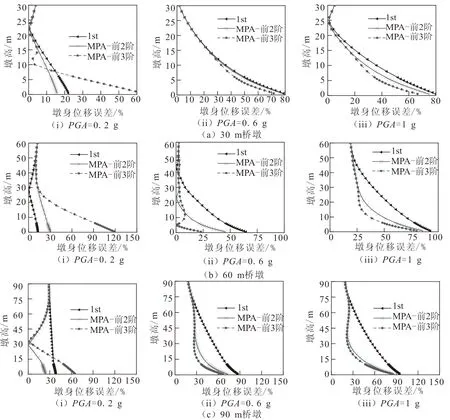
图6 各墩的墩身位移响应估计误差Fig.6 Estimation error of body displacement response of each pier

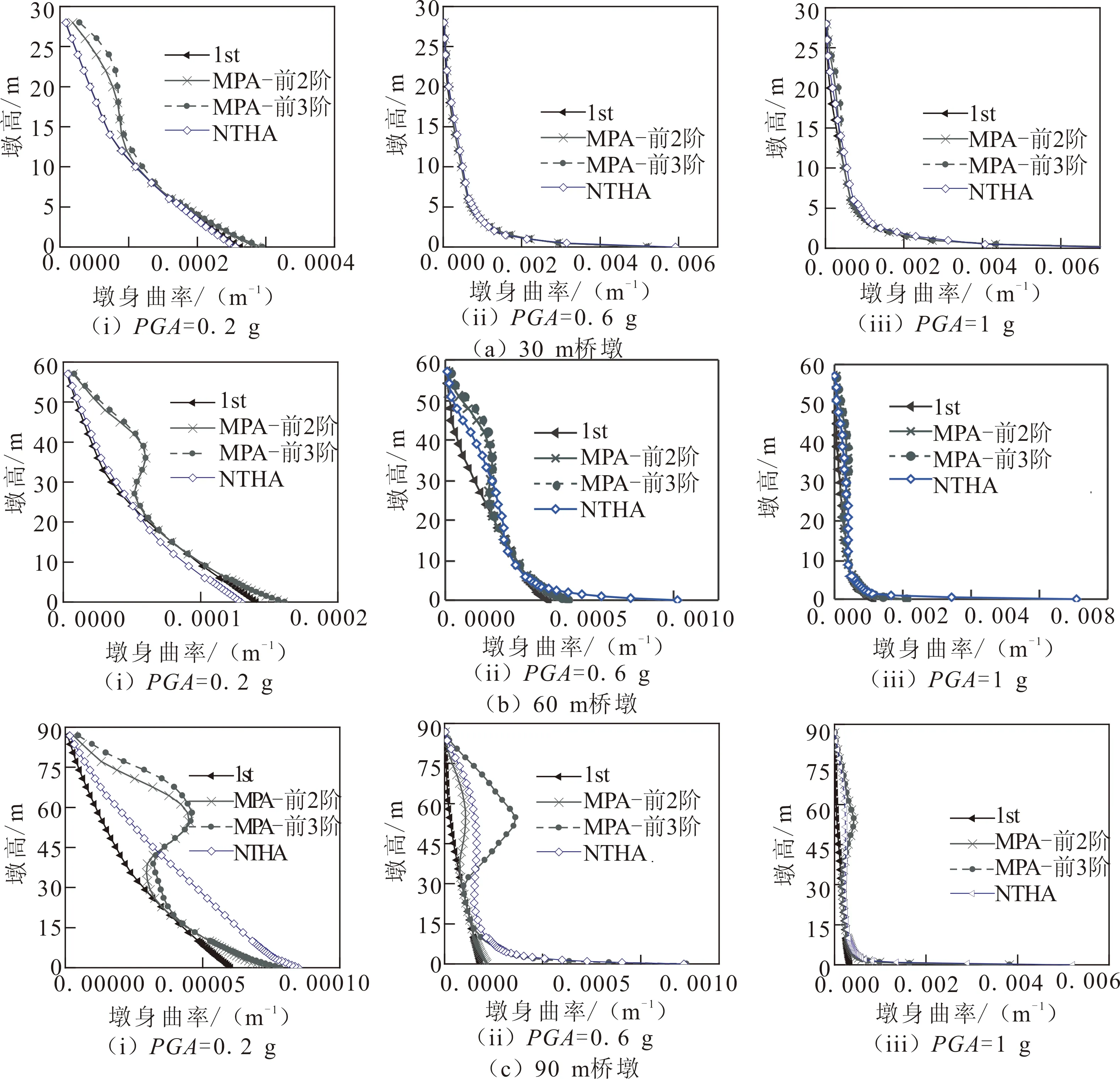
图7 各墩的墩身截面曲率响应Fig.7 Body section curvature respose of each pier

高墩在不同强度地震动作用下除了墩底附近出现塑性区域以外，墩身中部也可能出现塑性区域[5]。本文主要对墩底截面和1/2墩高截面的曲率进行监控，并将其作为评价基于模态的Pushover分析方法在估计墩身关键截面曲率时准确程度的指标。需要说明的是：墩身中部截面曲率最大位置并不固定，会随着不同地震动的频谱特性，以及不同的地震动强度而发生变化。将MPA方法计算墩底截面曲率和1/2墩高截面曲率的估计误差列在图8中。

由图8和可知，在计算30 m桥墩的截面曲率地震响应时，MPA方法得到的墩身截面曲率分布与NTHA方法的结果较为吻合，不同地震动强度下墩底截面和1/2墩高截面曲率地震响应的估计误差都较小。

在计算60 m桥墩和90 m桥墩的墩身截面曲率地震响应时，不仅在墩身中上部位置MPA方法得到的曲率分布与NTHA方法的结果出现了偏差，而且墩底截面和1/2墩高截面曲率地震响应的估计误差也较大。误差产生的原因和MPA方法自身的假设条件有关，MPA方法假设了模态在不同地震动作用下基本保持不变，同时假设结构在非线性阶段各阶模态解耦，并在求解总的地震响应时采用了SRSS方法对各阶模态地震响应贡献进行组合。

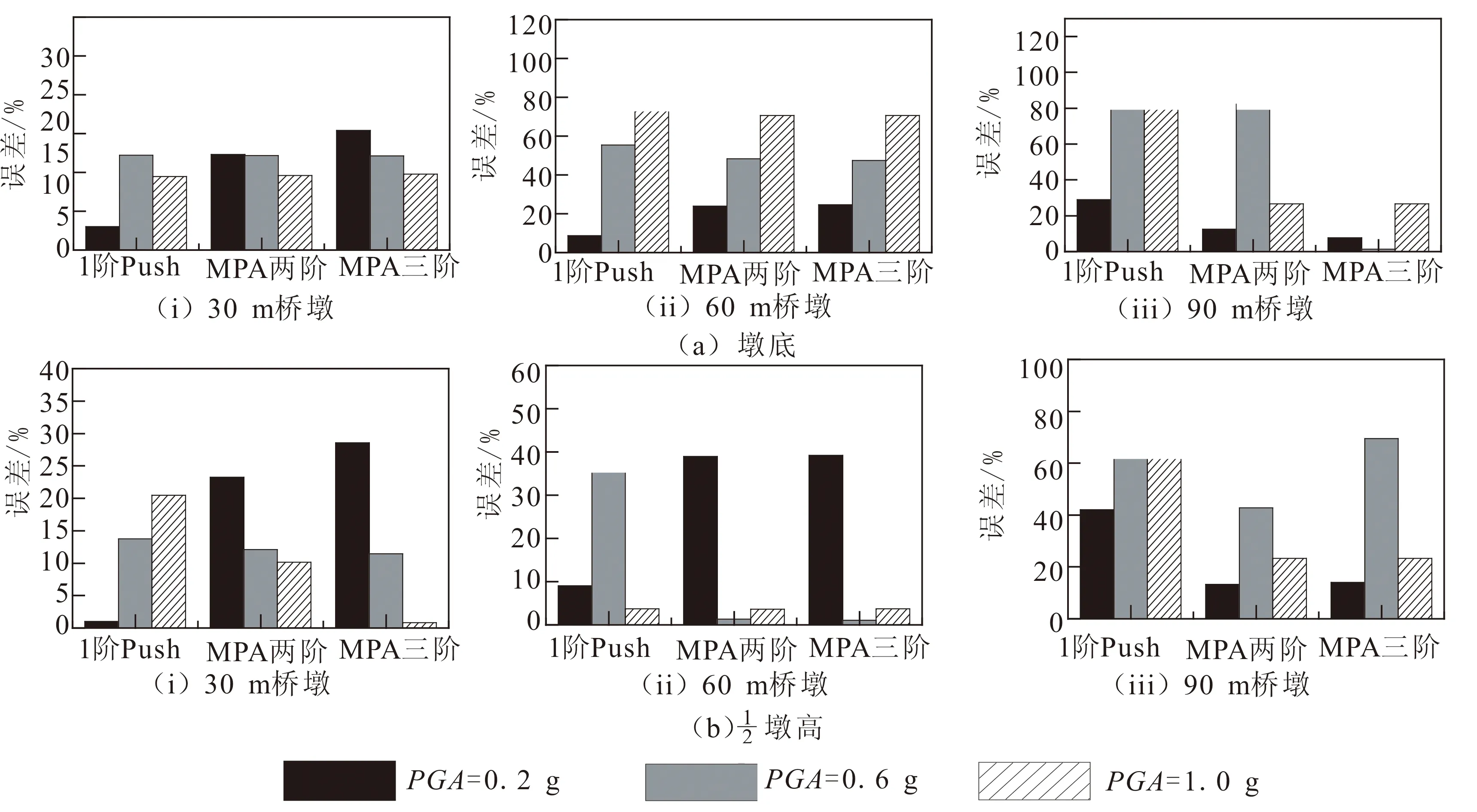
图8 墩底和1/2墩高截面曲率响应的估计误差Fig.8 Curvation response estimation errors of pier bottom section and section at pier height

5 结论

本文通过采用MPA方法和非线性时程分析方法对不同墩高的桥墩地震响应予以估计，得到以下结论：

(1) 采用MPA方法能够对地震作用下不同墩高的桥墩位移响应进行较好的估计，即使在强震作用下桥墩进入较大塑性后，误差仍然较小。

(2) MPA方法在估计不同墩高计算模型的墩顶位移地震响应时，采用多模态和只考虑第一阶模态的计算结果差别不大。可见墩顶位移地震响应的贡献基本来自于结构的一阶模态，高阶模态对墩顶位移地震响应的贡献程度很小。

(3) 采用MPA方法估计地震作用下不同墩高的桥墩截面曲率响应时，对30 m桥墩模型的适用性较好，误差较小。而在分析60 m、90 m桥墩时，MPA方法得到的曲率分布与NTHA方法的结果在墩身中上部位置出现了较为明显的偏差，且在桥墩关键截面处的估计误差也较大。

通过以上分析可知，MPA方法在估计不同墩高计算模型的墩顶位移地震响应的误差较小，而在估计高墩墩身关键截面曲率地震响应峰值的误差较大。对于高墩而言，墩身关键截面曲率是直接与损伤程度关联的地震响应参数，因此MPA方法不适用于高墩的抗震分析。

References)

[1] 中华人民共和国交通运输部.公路桥梁抗震设计细则 (JTG/T B02-01-2008)[S].北京：人民交通出版社，2008.Ministry of Transport of the People’s Republic of China.Guidelines for Seismic Design of Highway Bridges(JTG/T B02-01-2008[S].Beijing：China Communications Press，2008.(in Chinese)

[2] 梁智垚.桥梁高墩位移延性能力计算方法研究[J].工程抗震与加固改造，2005，27(5)：57-62.LIANG Zhi-yao.Study on Calculational Methods of Displacement Ductility Capacity of Tall Pier[J].Earthquake Resistant Engineering and Retrofitting，2005，27(5)：57-62.(in Chinese)

[3] 李建中，宋晓东，范立础.桥梁高墩位移延性能力的探讨[J].地震工程与工程振动，2005，25(1)：43-48.LI Jian-zhong，SONG Xiao-dong，FAN Li-chu.Investigation for Displacement Ductility Capacity of Tall Piers[J].Earthquake Engineering and Engineering Vibration，2005，25(1)， 43-48.(in Chinese)

[4] 卢皓，李建中，管仲国.高阶振型对高墩桥梁抗震性能的影响及识别[J].振动与冲击，2012，31(17)：81-85.LU Hao，LI Jian-zhong，GUAN Zhong-guo.Effect of Higher Modal Shapes on Aseismic Performance of a Bridge with High Piers and its Identification[J].Journal of Vibration and Shock，2012，31(17)：81-85.(in Chinese)

[5] 卢皓，李建中.强震作用下高墩桥梁抗震性能特点分析[J].地震工程学报，2013，35(4)：858-865.LU Hao，LI Jian-zhong.Seismic Performance Characteristics Analysis of Bridge with High Piers Under Strong Earthquake Motion[J].Earthquak Enginearing Journal，2013，35(4)：858-865.(in Chinese)

[6] California Department of Transportation.Caltrans Seismic Design Criteria Version 1.5[S].State of California：Business Transportation and Housing Agency，2009.

[7] A K Chopra，R K Goel.A Modal Pushover Analysis Procedure to Estimate Seismic Demands for Unsymmetric-plan Buildings[J].Earthquake Engineering and Structure Dynamics，2004，33(8)：903-927.

[8] 吴小峰，孙启国，狄杰建，等.抗震分析反应谱法和时程分析法数值仿真比较[J].西北地震学报，2011，33(3)：275-278.WU Xiao-feng，SUN Qi-guo，DI Jie-jian，et al.A Numerical Simulation Comparison Between Response Spectrum Analysis and Time History Analysis[J].Northwestern Seismological Journal，2011，33(3)：275-278.(in Chinese)

[9] Taucer F F，Enrico S.Fiber Beam-column Model for Seismic Response Analysis of Reinforced Concrete Structures[R].EERC 91-17，1991.

[10] Mander J B，Priestley M J N，Park R.Theoretical Stress-strain Model for Confined Concrete[J].J Structural Eng，ASCE，1988，114(8)：1804-1826.

[11] Menegotto M，Pinto P E.Method of Analysis for Cyclically Loaded Reinforced Concrete Plane Frames Including Changes in Geometry and Non-Elastic Behavior of Elements under Combined Normal Force and Bending[C]//Proceedings of IABSE Symposium on Resistance and Ultimate Deformability of Structures，Lisbon，1973：15-22.

[12] Silvia Mazzoni，Frank McKenna，Michael H.Open System for Earthquake Engineering Simulation User Manual[M].Berkeley：Pacific Earthquake Engineering Research Center，University of California，2005.

Application of Modal Pushover Analysis Method to Seismic Response of Piers with Different Heights

JIANG Chong-wen1, WANG Dian-bin2, LU Hao3

(1.CollegeofCivilEngineering,HunanUniversity,Changsha,Hunan410000,China;2.ChinaRailwayEryuanEngineeringGroupCo.Ltd,Chengdu,Sichuan610031,China;3.DepartmentofBridgeEngineering,TongjiUniversity,Shanghai200092,China)

Bridges are usually lifeline engineering-in-traffic projects, and their seismic performance is very important.As an important bridge construction component, piers are vulnerable to damage under strong ground motion.In this paper, in accord with the typical pier structure form of bridge piers in mountainous areas, a nonlinear numerical analysis model is constructed based on a fiber model.The seismic response of different piers under El-Centro is performed using modal pushover analysis (MPA).By comparison with the nonlinear time history analysis method, the applicability of the MPA method for the seismic analysis of different piers is investigated.The results show that the MPA method is not suiTablefor higher piers where the contribution of higher modes in seismic response is significant.With the implementation of the Western Development Program in recent years, a lot of highways and railways have been planned and built in western China.For bridges with high piers in mountainous areas, a nonlinear numerical analysis model is constructed based on a fiber model.The finite-element analysis is simulated with the code OpenSees, which was developed by Pacific Earthquake Engineering Research (PEER).The Mander model is used to imitate the constitutive model of concrete, and the Giuffré-Menegotto-Pinto model is used to imitate the constitutive model of reinforcement.The incremental dynamic analysis is used to research distribution features of pier section curvature under strong earthquake motions.As a result of the effects of higher modal contributions, the seismic response and seismic performance of bridges with high piers are complicated.The forming and development of a plastic range in the upper position of a pier, the damage process, and the failure mechanism of high piers under different earthquake motions are studied.The base section curvature of high piers and its top displacement are not simultaneous; it is inappropriate for pier top displacement to be used as the performance index.By taking pier section curvature as the performance index, seismic performance characteristics of bridges with high piers in the plastic stage are discussed; the complexity of the seismic performance of bridges with high piers because of the contribution from higher modes is revealed further.The spectral characteristics of ground motion have a great influence on the seismic performance of bridges with high piers.This paper studies six earthquake waves from the PEER database that are class II sites.Because of space constraints, this study involves only the seismic performance of bridges with high piers under transversal earthquake action.After a careful analysis, it is discovered that one pier base section curvature is greater than any other piers when all the piers are plastic; the location of the most dangerous pier depends on the magnitude of the contributions from higher modes.Unlike bridges with low piers, sometimes the damage of higher piers could be more serious than that of lower piers for bridges with high piers.The envelopes of section curvature above the pier base plastic region do not have a linear trend; the occurrence of plastic hinges at the middle and upper parts of piers is attributed to the contribution of higher modal shape.Additionally, the extent and the size of this plastic region are affected by the spectral characteristics of the ground motion.Because of the contribution from higher modes, the bridge with high piers is not safe when designed according to the existing specifications.

MPA (modal pushover analysis); nonlinear time-history analysis; fiber model; seismic analysis of piers

2014-08-20

西部地区博士后人才资助计划(2014M562526XB)

蒋崇文(1984-) ，女，博士研究生，主要从事桥梁抗震方面的研究.E-mail： chongwen5@126.com

P315.9

A

1000-0844(2015)02-0577-08

10.3969/j.issn.1000-0844.2015.02.0577