带周期参数的差分方程组的全局性质

韩彩虹,李 略，庞琳娜,朱慧娟

(广西师范大学数学与统计学院，广西 桂林 541004)

带周期参数的差分方程组的全局性质

韩彩虹,李 略，庞琳娜,朱慧娟

(广西师范大学数学与统计学院，广西 桂林 541004)

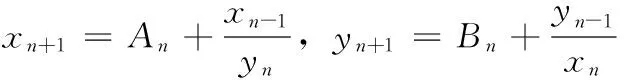
差分方程组；正解；周期解；收敛性

1 引 言

差分方程具有广泛的应用背景，近年来差分方程组成为研究热点之一[1-3].在文献[4]中Ameleh等人研究了方程

解的全局性质，其中A,B∈[1，+∞)，初始值x-1，x0是任意的正实数。

在文献[5]中张千宏等人研究了差分方程组

解的全局性，其中A,B∈(1，+∞)，初始值是任意的正实数。

受上述文献启发，本文主要研究差分方程组

(1)

的解的全局性质,其中参数An,Bn∈(1，+∞)且是二周期序列,初始值x-1,y-1∈(0，+∞),x0,y0∈(0，+∞)。

本文推广了上述文献，在方法上和理论上都具有一定的应用价值。若取xn=yn则是文献[4]研究的方程，若取序列An、Bn分别为常数A、B则是文献[5]研究的方程。

2 主要结论

由于参数An,Bn∈(1，+∞)且是二周期序列，不妨设

定理1 对于差分方程组(1)的每个正解(xn,yn),序列{x2n},{x2n+1},{y2n},{y2n+1}有界且n≥0时

证明 由方程组(1)显然得,对于任意的n≥0有x2n+1>a,x2n+2>A,y2n+1>b,y2n+2>B。因为

由数学归纳法得

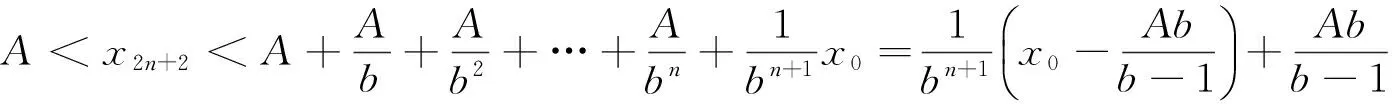
引理 若差分方程组(1)有二周期解，则仅有唯一的二周期解，且

证明 设(x2n,y2n)=(X0,Y0),(x2n+1,y2n+1)=(X1,Y1)是方程组(1)的二周期解，因为

(2)

所以

(3)

(4)

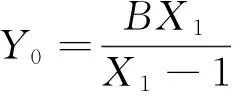
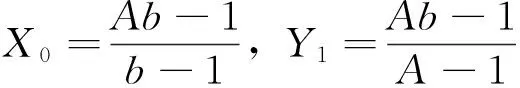
定理2 差分方程组(1)的每个解都收敛于唯一的二周期解

证明 首先证明n→∞时序列{x2n},{y2n},{x2n+1},{y2n+1}收敛。

由定理1知序列{x2n},{y2n},{x2n+1},{y2n+1}有界，所以上下极限都存在，不妨设

显然

(5)

代入方程组(1)得

所以

(6)

(7)

(8)

(9)

由于A、a、B、b都大于1,故由式(6)、(7)得l1l2′≥L1L2′,由式(8)、(9)得l1′l2≥L1′L2;结合式(5)得

(10)

(11)

下证L1=l1。否则L1>l1,由式(10)得l1l2′=L1L2′>l1L2′,则l2′>L2′,矛盾。所以只有L1=l1。同理可证L1′=l1′,L2=l2,L2′=l2′。即

故当n→∞时，序列{x2n},{x2n+1},{y2n},{y2n+1}收敛。

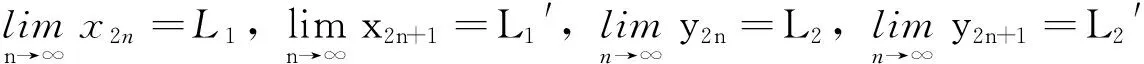
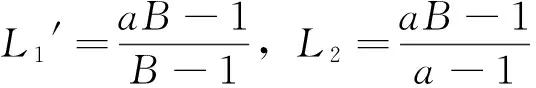
取A′=max{A,a},B′=min{B,b},设

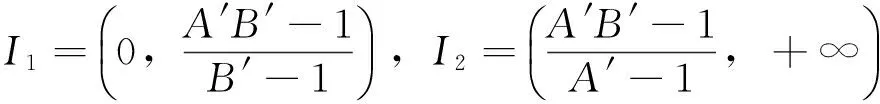
(1)若(xi,yi)∈I1×I2,i=-1,0，则方程组(1)的每个正解(xn,yn)∈I1×I2，n≥1;

(2)若(xi,yi)∈I2×I1,i=-1,0，则方程组(1)的每个正解(xn,yn)∈I2×I1，n≥1。

证明 (1)由方程组(1)得

所以(x1,y1)∈I1×I2。假设n=k≥2时(xk,yk)∈I1×I2成立，则

即(xk+1,yk+1)∈I1×I2。由数学归纳法得方程组(1)的每个正解(xn,yn)∈I1×I2,n≥1。

同理可证明(2)。

[1]ZhangQ,YangL,LiuJ.Dynamicsofasystemofrationalthird-orderdifferenceequation[J].AdvDifferEqu,2012,2012(01):1-6.

[2]赵小红,康淑瑰,高英.带非局部条件的分数次差分方程组解的存在唯一性[J].生物数学学报,2013,(02):017.

[3]SteviĉS.Onasystemofdifferenceequationswithtwoperiodiccoefficients[J].AppliedMathComp,2011,218(08):4317-4324.

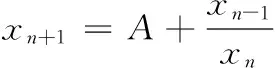
[5]张千宏,杨利辉.一类非线性差分方程系统解的性质[J].四川师范大学学报:自然科学版,2012,34(04):505-509.

[责任编辑：郑秀亮 英文编辑：刘彦哲]

Global Character of System of Difference Equations with Periodic Parameters

HAN Cai-hong, LI Lue, PANG Lin-na, ZHU Hui-juan

(School of Mathematics and Statistics,Guangxi Normal University,Guiling,Guangxi 541004,China)

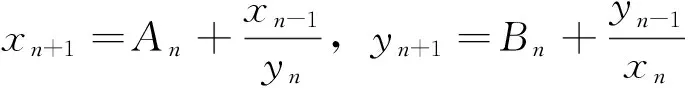
system of difference equations;positive solution;periodic solution;convergence

广西高校科学技术研究项目(LX2014048，LX2014055)；广西师范大学青年基金项目(201401)

韩彩虹(1982-)，女，河北张家口人，广西师范大学数学与统计学院讲师，硕士。

O

A

10.3969/j.issn.1673-1492.2015.05.001

来稿日期：2015-06-18