平行钢绞线斜拉索等值张拉力精确计算方法
邹 力,彭旭民,位东升
(中铁大桥局集团武汉桥梁科学研究院有限公司,湖北 武汉430034)
平行钢绞线斜拉索等值张拉力精确计算方法
邹 力,彭旭民,位东升
(中铁大桥局集团武汉桥梁科学研究院有限公司,湖北 武汉430034)
为提高平行钢绞线斜拉索成桥索力的精度和每股钢绞线所持索力的均匀性,从平行钢绞线斜拉索等值张拉法的基本理论出发,对现有的张拉力计算公式进行修正完善,提出更精确的张拉力计算公式,对单根钢绞线张拉力控制方法进行修正完善,提出了更精确的张拉力控制公式和控制方法。
桥梁工程;平行钢绞线斜拉索;等值张拉法;张拉力控制
平行钢绞线斜拉索常用的张拉方式有两种:一种是传统的整体张拉,另一种是单根张拉,单根张拉普遍采用“等值张拉法”进行控制,也称为等值张拉。国内2003年兰州小西湖黄河大桥平行钢绞线斜拉索首次采用等值张拉工艺[1],至今已有10年。随着平行钢绞线斜拉索的广泛运用,等值张拉工艺的运用越趋广泛,因此优化完善平行钢绞线斜拉索钢绞线张拉力的计算公式和张拉力控制方法具有实际应用价值。
1 等值张拉理论
平行钢绞线斜拉索采用等值张拉时,随着每股钢绞线的张拉,桥梁结构均产生变形。主梁产生上挠、索塔产生压缩[2],斜拉索梁端锚点与塔端锚点的相对距离不断缩短,已张拉钢绞线的工作长度同步缩短,导致已张拉钢绞线所持索力不断变小。
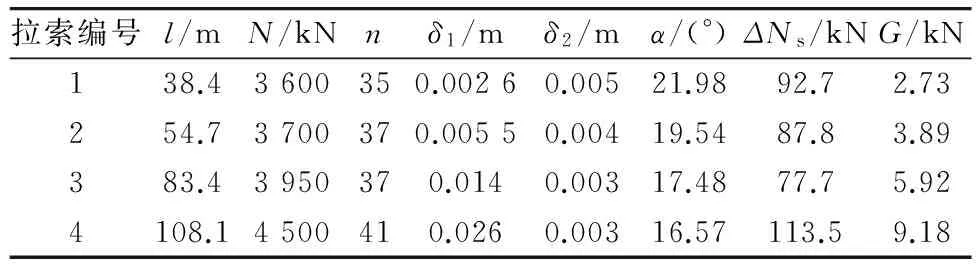
假若一根斜拉索由n股钢绞线组成,第i股〔1 根据等值张拉基本理论,单根钢绞线张拉力由两部分组成:①单根钢绞线设计索力;②超张拉索力。影响钢绞线最终张拉力的是超张拉索力值,确定超张拉索力值是张拉力计算的关键。 2.1 影响因素 影响钢绞线超张拉索力值的因素都将影响钢绞线索力值的确定。梁端锚点和塔端锚点间已张拉钢绞线的工作长度变化引起钢绞线所持索力值的变化,从这一点进行分析研究,主要的影响因素包括:桥梁结构特性;夹片回缩量;斜拉索垂度;桥梁结构收缩徐变。 2.1.1 桥梁结构特性 随着每股钢绞线的张拉,主梁产生上挠、索塔产生压缩,斜拉索梁端锚点与塔端锚点的相对距离不断缩短,造成已张拉钢绞线的工作长度缩短,缩短量δ由桥梁结构特性(主梁抗弯刚度、主塔截面特性、主塔材料抗压强度等)决定。 2.1.2 夹片回缩量 夹片回缩引起钢绞线张拉力损失,因此在计算斜拉索钢绞线张拉力时必须考虑。研究资料表明,钢绞线张拉时,夹片回缩量在两个部位出现[3]:①张拉千斤顶使用的“工具夹片”;②将钢绞线锚固在混凝土中的“工作夹片”。用于张拉斜拉索钢绞线的千斤顶具有自锚功能,在计算钢绞线超张拉力时只需考虑“工作夹片”产生的回缩量,一般根据类似桥梁的经验值采用。 2.1.3 斜拉索垂度 斜拉索是柔性结构,在重力作用下会产生垂度,即索结构的几何非线性。随着斜拉桥跨径的增加,索结构的几何非线性的影响越明显;在斜拉索的张拉过程中应该考虑索结构几何非线性的影响[4]。 采用有限元模型计算斜拉索索力时,通常将斜拉索简化为抗弯刚度为0的弹性杆系单元,弹性杆系单元考虑自重垂度对拉索轴向刚度的影响,而不考虑自重垂度带来的几何非线性的影响,计算得到的索力值不能直接作为斜拉索张拉力控制值,而应该进行采用几何非线性修正。 2.1.4 收缩徐变 收缩徐变使斜拉桥成桥后斜拉索索力减小、主梁下挠,为减小收缩徐变的不良影响,斜拉桥悬臂施工时,要考虑成桥后收缩徐变的效应,采取相应的预防措施:如主梁预拱度考虑收缩徐变产生的下挠。斜拉索张拉时同样应该考虑收缩徐变效应,即:钢绞线张拉过程中,以成桥索力作为张拉目标值时,应对收缩徐变效应进行修正。 2.2 初张拉力计算公式分析 根据近年来有关平行钢绞线斜拉索等值张拉法资料和论文,初张拉力采用如下计算法则和公式确定。 第1~m股张拉力:第1~m根钢绞线承受HDPE外管的自重,张拉力由HDPE管的垂度确定,一般为1~4 根,视HDPE外套管尺寸和长度而定,一般单根钢绞线的预张拉力取设计索力的0.15倍~0.2倍。 第(m+1)股张拉力:根据整束拉索索力平均之后由主梁及索塔的变形量进行修正,使安装完成之后单根索力累计值与设计接近,避免单根挂索后索力大调整。索力大小按式(1)、式(2)确定[5]: (1) (2) 式中:N为斜拉索设计索力(未考虑收缩徐变);N1m为第1~m股钢绞线张拉力之和;n为斜拉索钢绞线股数;δ为斜拉索张拉完成后梁端锚点与塔端锚点间斜拉索索长理论变形值;l为斜拉索索长;Ec为钢绞线弹模;A为截面面积;T(m+1)为第(m+1)股钢绞线张拉力;K为钢绞线张拉力超张拉系数。 从式(1)可以看出,钢绞线初张拉力只对因斜拉索张拉完成后梁端锚点与塔端锚点间斜拉索索长变短的影响因素进行了修正,而没有对其他的影响因素进行修正,如采用式(1)计算所得到的钢绞线张拉力进行张拉控制,斜拉索最终索力将偏小。其中,斜拉索索长缩短值由桥梁结构特性确定。 2.3 完善后初张拉力计算公式 根据等值张拉基本理论和钢绞线初张拉力影响因素的分析研究,对钢绞线初张拉力公式进行修正完善。 第1~m股张拉力: T1~Tm=N/n (3) 即第1~m股张拉力钢绞线的预张拉力取设计索力值。现有计算公式的取值为(0.15~0.2)N/n,在实际的运用中,随着其余各股钢绞线的张拉,第1~m股钢绞线将不受力而产生下垂,造成后续钢绞线穿索时交叉打结。而采用式(3)时,第1~m股钢绞线始终处于受力状态,不会影响后续钢绞线穿索。 第(m+1)股张拉力: (4) (5) 式中:δ1为斜拉索张拉完成后梁端锚点与塔端锚点间斜拉索索长理论变形值;δ2为工作夹片回缩量;ΔNs为收缩徐变引起的斜拉索索力减小值,ΔNs=(N-Ns)(Ns为考虑收缩徐变后的斜拉索索力设计值);G为锚点间斜拉索重力;α为斜拉索设计仰角。 2.4 计算值对比 采用上述钢绞线初张拉力计算式(1)和式(4),抽取某斜拉桥4根由短至长的平行钢绞线斜拉索进行钢绞线初张拉力计算,Ec钢绞线弹模取值1.95E+5 MPa,A单股钢绞线截面面积取值0.14×10-4m2,斜拉索参数见表1,计算结果见表2。 表1 某桥斜拉索参数 表2 某桥斜拉索钢绞线张拉力计算值对比 为使式(1)和式(4)具有可比性,第1~m股钢绞线的初张拉力T1~Tm取相同值N/n,从表2计算结果可看出:钢绞线初张拉力差值百分比为3.01%~5.77%,工作夹片回缩、斜拉索垂度、收缩徐变对钢绞线初张拉力有明显的影响,且对短索的影响较长索更为明显,因此在计算中必须考虑,完善后的钢绞线初张拉力计算式(4)考虑了以上影响因素,成桥索力较式(1)更接近斜拉索实际受力。 单根钢绞线张拉力控制的普遍做法[6-8]:将压力传感器安装在张拉端正式张拉的第1根钢绞线上〔即第(m+1)根〕,当后续钢绞线张拉时,传感器读数下降,当油压表读数与传感器示值相同时,停止张拉并持荷锚固。 3.1 钢绞线张拉力控制关键点分析 钢绞线等值张拉过程中以压力传感器示值来控制钢绞线张拉力,压力传感器示值是否能准确反应钢绞线实际张拉力是钢绞线张拉控制的关键。 压力传感器安装在工具锚和工作锚之间,其示值为钢绞线的最终锚固力,张拉千斤顶配套油泵的油压表示值为钢绞线的张拉力,在钢绞线锚固时工作夹片回缩产生应力损失,必然造成锚固力与张拉力之间存在偏差,即压力传感器示值比钢绞线实际张拉力小,因此以传感器示值直接控制钢绞线实际张拉力的方法存在不足。 3.2 钢绞线张拉力控制方法改进 如果能避免或者抵消压力传感器示值与钢绞线实际张拉力之间偏差的影响,钢绞线等值张拉控制精度将得到提高,从这一点出发对钢绞线张拉力控制方法进行改进。 (6) (7) 第(m+i)根钢绞线与第(m+i+1)根钢绞线长度相同,张拉伸长量相同,因此由工作夹片回缩引起的应力损失近似相等,ΔT(m+i)≈ΔT(m+i+1)。因此: ΔT(m+i+1)] (8) (9) (10) (11) 按照式(10)、式(11),平行钢绞线斜拉索等值张拉工艺如下(张拉力以油压表控制): 1)预张拉第1~m根钢绞线,张拉力为(N/n); 7)对第1~m根进行补张拉,张拉力同样按上述公式确定,拆除第(m+1)根钢绞线上传感器,并按当时下降值进行补张锚固。 等值张拉法是平行钢绞线单根张拉普遍采用的控制方法,单根钢绞线张拉力的计算和钢绞线张拉力的控制是等值张拉法的关键,在分析现有的张拉力计算公式和张拉力控制方法后,从平行钢绞线斜拉索等值张拉法的基本理论出发,提出更精确的钢绞线张拉力计算公式和控制公式。 [1] 张多平,康炜.兰州市小西湖黄河大桥设计分析[J].兰州铁道学院学报:自然科学版,2002,21(6):69-72. Zhang Duoping, Kang Wei, Design analysis of Xiaoxihu Yellow River bridge in Lanzhou City[J]. Journal of Lanzhou Railway University: Natural Sciences,2002,21(6):69-72. [2] 王鹏,王根会.斜拉索单根张拉施工控制技术研究[C]//第14届全国结构工程学术会议论文集.北京:工程力学杂志社,2005:294-298. Wang Peng, Wang Genhui. Research on single stretching construction technique of cable-stayed bridge[C]// Proceedings of 14thNational Conference on Structural Engineering. Beijing: Engineering Mechanics Press,2005:294-298. [3] 徐建红,范厚彬.锚具夹片回缩引起预应力损失的研究[J].公路,2006(7):93-96. Xu Jianhong, Fan Houbin. A study on presstressing loss of anchorage circle caused by anchorage retraction[J]. Highway,2006(7):93-96. [4] 胡方健,李国平.自重和索力偏差对混凝土斜拉桥施工受力状态的影响[J].同济大学学报:自然科学版,2012,40(2):191-197. Hu Fangjian, Li Guoping. Influences of deviation of gravity and cable tension force on construction state of cable-stayed concrete bridges[J]. Journal of Tongji University: Natural Science,2012,40(2):191-197. [5] 冷雪浩,林乐强,黄伟东.平行钢绞线斜拉索单根钢绞线张拉过程中的索力控制[J].北方交通,2008(1):83-84. Leng Xuehao, Lin Leqiang, Huang Weidong. Control of cable force in the process of stretching the single strand of parallel strand stayed-cable[J]. Northern Communications,2008(1):83-84. [6] 王志刚,费汉兵,单继安.钢绞线斜拉索索力均衡控制技术的探讨[J].山西建筑,2011(9):169-170. Wang Zhigang, Fei Hanbing, Shan Ji’an. Discussion on cable force equalization control technology of the multi-strand stay cable[J]. Shanxi Architecture,2011(9):169-170. [7] 陈林.平行钢绞线斜拉索施工技术[J].公路交通技术,2008(5):66-69. Chen Lin, Construction technique of parallel steel stranded wire stay cable[J].Technology of Highway and Transport,2008(5):66-69. [8] 唐顶峰,陈双庆.安康七里沟汉江大桥环氧钢绞线斜拉索安装工艺[J].预应力技术:施工技术版,2009(2):23-27. Tang Dingfeng, Chen Shuangqing. Installing technology of epoxy-coated strand stayed-cable Ankang Qiligou Hanjiang bridge[J]. Prestress Technology: Construction Technique Edition,2009(2):23-27. Accurate Calculation Method of Equal Tensile Force of Parallel Strand Stayed-Cable Zou Li, Peng Xumin, Wei Dongsheng (Wuhan Bridge Science Research Institute Co. Ltd., China Railway Major Bridge Engineering Group, Wuhan 430034, Hubei, China) In order to improve the accuracy of the stay cable force, and improve the uniformity of the single steel strand cable force, the existing formula for calculating cable force was revised and perfected, and a more accurate formula for calculating cable force was presented. The existing control method of single steel strand cable force was also revised and perfected, and a more accurate control formula and control method for cable force was presented. These studies were conducted according to the basic theory of equal tensile force method of parallel strand stayed-cable. bridge engineering; parallel strand stayed-cable; equal tensile force method; control of cable force 10.3969/j.issn.1674-0696.2015.02.02 2014-01-14; 2014-04-07 邹 力(1982—),男,湖北天门人,工程师,硕士,主要从事桥梁监控与检测方面的研究。E-mail:zouli161@163l.com。 U448.27 A 1674-0696(2015)02-007-032 张拉力计算

3 钢绞线张拉力控制
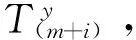
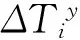
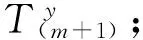
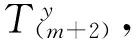
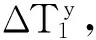
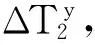
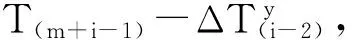
4 结 语

