飞秒激光频域干涉测距相位信号分析与处理

刘娇月,杨聚庆

(1．河南工业职业技术学院柔性实验室，河南南阳 473009；2．北京工业大学应用数理学院，北京 100124；3. 中国科学院光电研究院，北京 100094)



飞秒激光频域干涉测距相位信号分析与处理

刘娇月1,3,杨聚庆2,3

(1．河南工业职业技术学院柔性实验室，河南南阳 473009；2．北京工业大学应用数理学院，北京 100124；3. 中国科学院光电研究院，北京 100094)

针对飞秒激光测距频谱干涉条纹信号，分析了被测距离精度对于相位信息采集与处理要求，详细介绍了光谱分辨干涉测距的数据处理过程。根据测距信号干涉谱的数学关系，推导了被测距离求解公式。采用快速傅里叶变换和坐标旋转数字计算法进行光谱分辨干涉信号处理，经过时域信号的傅里叶变换、信号相位解包裹、加窗函数时域信号滤波等环节，分别对飞秒激光测距频谱干涉条纹信号中每个频率的相位值进行处理和变换。系统仿真中，离散频谱分析的幅值最大误差从36.3%降低到15.1%。经过比对实验，该法能实现飞秒激光测距信号有效处理。

飞秒激光测距；光谱分辨干涉；相位信号处理

0 引言

飞秒激光应用技术是当今超精密测量技术的前沿领域，是现代高精度几何量和面形测量技术的发展方向，对极端制造中的精密装备加工质量与精度具有重要影响。飞秒激光频率梳为激光测距提供了新的测量方法，测量性能显著提高。2000年，日本国家计量研究所(NMIJ)的科学家K. Minoshima等人首次提出采用光频梳进行绝对测距的概念。之后，美国NIST、韩国KAIST和荷兰VSL等研究机构又采取了不同的技术方案使其朝着大范围、高精度、快速实时的方向更进了一步[1]。我国也有多家单位研究基于光频梳的几何量测量。

采用飞秒激光频率梳的光谱分辨干涉测距相比传统的白光频域干涉测距测量范围明显提高，测量精度可以达到nm量级。其中，飞秒激光频谱干涉条纹相位信息的快速处理和准确提取对被测距离精度起到关键影响作用，要求通过对信号进行高效、精确的变换和算法处理，对干涉条纹信号中每个频率的相位值进行处理和变换，以快速获得大范围、高精度的被测距离值[2]。本系统中采用FFT(Fast Fourier Transformation)法和坐标旋转数字计算法对CCD探测器采集的干涉信号进行数据处理和计算分析。

1 飞秒激光频率梳频域干涉

飞秒激光频率梳由锁模激光器产生，通过在宽频谱范围所包含的激光纵模之间建立起固定的相位关系[2]，可以使激光器的时域输出从连续光转变为脉宽极窄、峰值功率极高的光脉冲序列。随着被锁定的纵模模式增加，光脉冲宽度越来越窄。飞秒激光器锁定的纵模模式大约为106量级，在时域上能够输出脉冲宽度达到飞秒级的光脉冲。飞秒脉冲激光所对应的频谱为一系列频率间隔相等，相位关系固定的光频率纵模分量。这些离散的频率分量在频域上像梳齿一样排列，因此也被称为激光频率梳[3]。

飞秒激光频率梳光谱频域干涉是时间相干性的直接体现[4]，基于非平衡的迈克尔逊干涉仪测量方法，从较宽的光谱中有规律地挑出部分光谱进行频率干涉测量，测量精度可以达到nm量级。测量原理如图1所示。

图1 光谱分辨干涉测距原理图

飞秒激光源发射具有一定重复频率的激光光束经过光隔离器进入分光棱镜，经过分光棱镜分出的两束光分别进入测量臂和参考臂，参考臂在测距的过程中保持不变，测量臂随着被测距离的变化而变化，经测量臂和参考臂反射的光束再次经过分光棱镜以后进入F-P标准具，F-P标准具对从迈克尔逊干涉仪出射的光束进行频域滤波，滤波后的光束再通过光栅衍射后打到CCD探测器上，CCD探测器记录不同距离时的干涉条纹。通过对CCD探测器的干涉条纹进行处理就可以获得被测距离值[5]。

CCD探测器记录的飞秒激光干涉条纹可以使用光谱功率密度S(ω,v)表示，随着频率ω变化，函数表示为：

S(ω)= |Aref(ω)|2+|Amea(ω)|2+|Aref(ω)|·

|Amea(ω)|cos[φref(ω)-φmea(ω)]|

(1)

式中：|Aref(ω)|、φref(ω) 表示参考臂飞秒脉冲幅值和相位；|Amea(ω)|、φmea(ω) 表示测量臂飞秒脉冲幅值和相位。

参考臂和测量臂之间相位的变化通过干涉条纹的变化体现。相位与被测距离关系表示为：

φ(ω)=ωref(ω)-φmea(ω)=2n(ω)ωL/c

(2)

式中：n(ω)为空气中不同频率对应的折射率；c为光在真空中传播的速度；L为测量臂与参考臂之间的路程差。

公式变形后，被测距离计算公式为：

(3)

2 频域干涉测量信号变换处理

光谱分辨干涉测距信号处理过程为：首先由CCD探测器探测飞秒激光光谱分辨干涉条纹，然后利用傅里叶反变换将干涉信号变换到时域，时域中含有两个交流分量和一个直流分量，利用带通滤波器滤出交流分量，再将交流分量变换到频域求出每个频率对应的相位值，利用线性拟合求出直线斜率可以求得被测距离值。

2.1 时域信号的傅里叶变换

在图1的迈克尔逊干涉仪中，假定测量镜与反射镜反射率相等并忽略空气的吸收，则|A}ref(ω)|=|Amea(ω)|表示光源的光谱|A(ω)|，光源光谱图如图2所示。

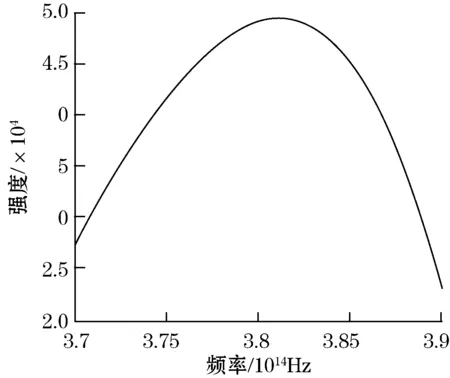
图2 光源光谱图

公式(1)描述的干涉公式可以简化为：

S(ω)=|A(ω)|2{1+cos〔φref(ω)-φmea(ω)〕}

(4)

又φref(ω)-ωmea(ω)=2n(ω)ωL/c，由式(4)可以得到：

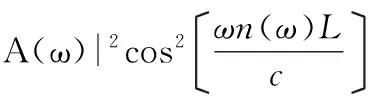
(5)

从式(5)可以看出干涉条纹由余弦调制的光源频谱形成，调制大小与距离相关，被测距离为0.5 mm时利用光源光谱仿真的光谱分辨干涉如图3所示。

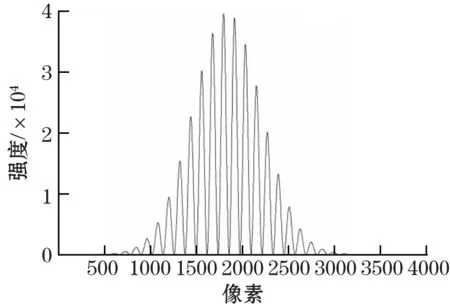
图3 0.5 mm时光谱分辨干涉图

对式(4)进行傅里叶变换可以得到：

S(τ) =FT-1{S(ω)}

=FT-1{|A(ω)|2〔1+cos[φref(ω)-φmea(ω)]〕}

=FT-1{|A(ω)|2〔1+cos(ωΔt)〕}

(6)

式中：a(τ)=FT-1{|A(ω)|2};Δt=2n(ω)L/c;δ(τ)为单位冲击函数;τ是表示光学路径时间延迟的变量[6]。

由于飞秒光源的时域脉冲a(τ)宽度很窄，故式(6)在时域图上表示3个分开的不同峰值，峰值位置分别在Δt,0,-Δt处。被测距离为0.5 mm时，反傅里叶变换后时域图如图4所示，3个峰值含有一个直流分量和两个交流分量，直流分量中没有距离信息，而两个交流分量中含有同样的距离信息，使用带通滤波器滤出两个交流分量中的一个，则可得：

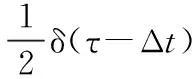
或

(7)

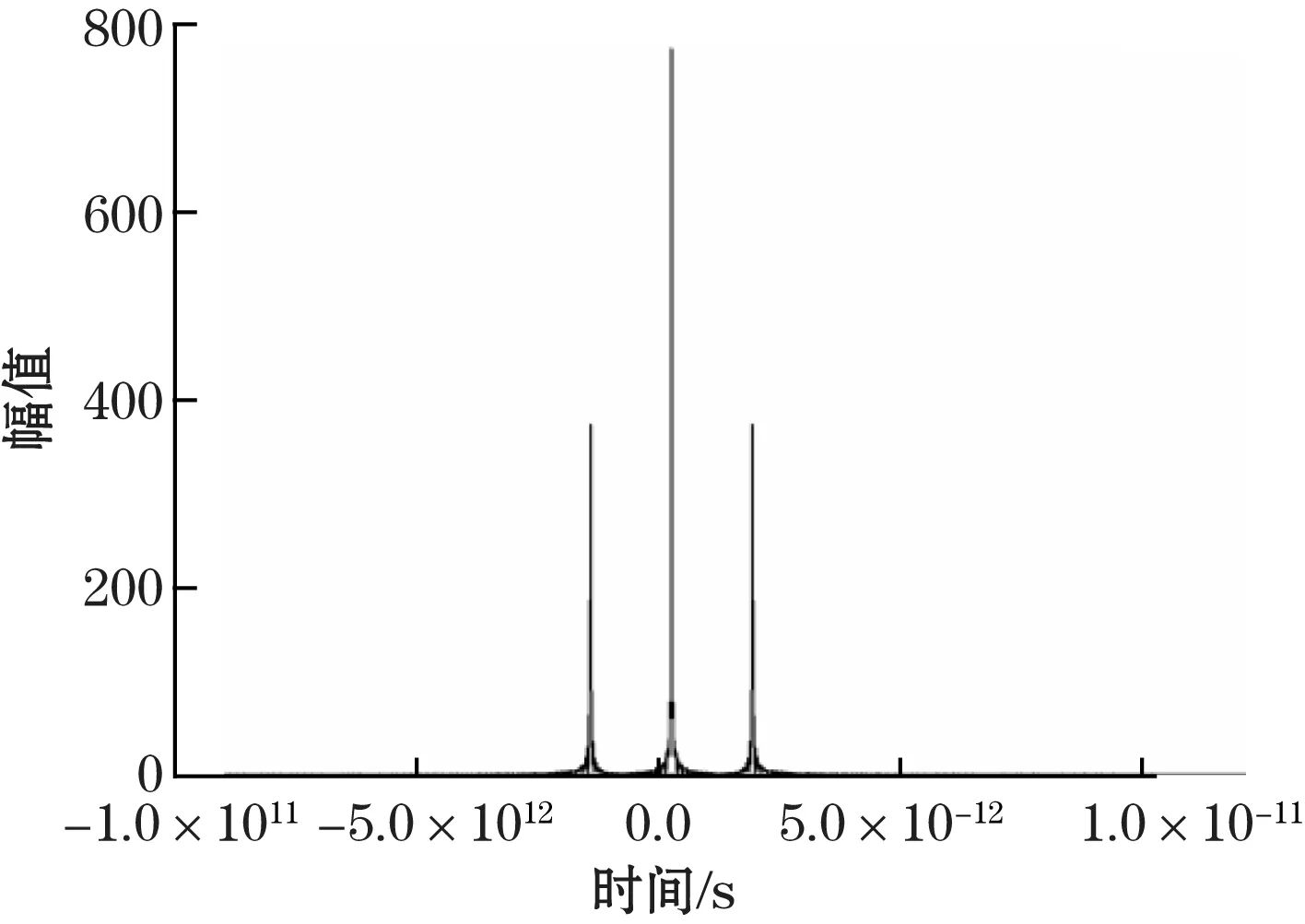
图4 IFFT变换时域波形图

式(7)描述的时域信号需要再次利用傅里叶变换，变换结果如下：

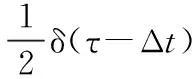
(8)

通过公式(8)可以看出使用反正切函数计算出频率对应的相位值为[4]:

(9)

利用公式(9)求解出的相位值在-π/2到π/2范围内，此时的相位值称为包裹相位值。

2.2 信号相位解包裹

包裹相位需要解包裹才能得到相邻频率传输一段距离后的真实相位差，由于反正切函数有周期性，在利用反正切求解相位时，如果相邻频率之间的相位差大于π时，就会出现

图5中"锯齿状"波形，反过来可以利用"锯齿状"波形求解出包裹相位值[7]。

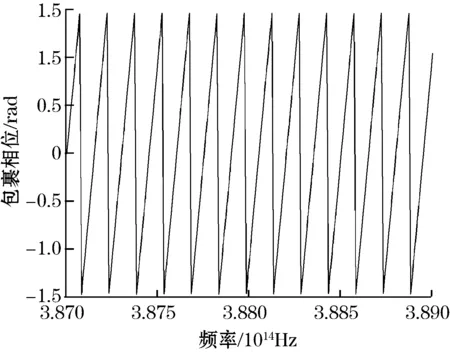
图5 包裹相位图

相位解包裹的过程如下：

(1)求解第一个频率对应的非包裹相位值φ0(ω)，包裹相位值与非包裹相位值之间具有一定的相位偏差，假定这个偏差为Δφ，第一个频率对应的包裹相位值为φ(ω0)，则非包裹相位值φ0(ω)可以表示为：

φ0(ω)=φ(ω0)+Δφ

(10)

(2)第n个频率对应的相位值与第一个频率的相位值之间"锯齿波”跳跃的个数k，每跳跃一次说明相差一个π值，此时第n个频率对应的非包裹相位值为：

φn(ω)=k·π+φ0(ω)

(11)

(3)重复步骤(2)直到确定所有频率对应的非包裹相位值，然后利用所有频率对应的非包裹相位值进行线性拟合求出直线斜率，由公式(3)求得被测距离值。被测距离为0.5 mm时，利用非包裹相位值进行线性拟合的直线如图6所示。

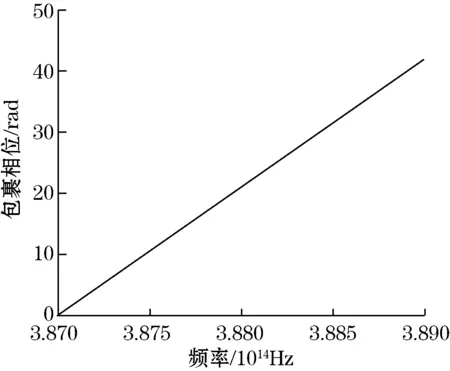
图6 直线拟合

信号解包裹时采用坐标旋转算法(CORIDC，Coordinate Rotational Digital Computer)进行三角函数运算，实现高精度反正切运算，满足相位计算精度需要。

2.3 时域信号的滤波

在利用傅里叶反变换将干涉信号变换到时域信号后，需要从时域波形的两个交流分量和一个直流分量中滤出一个交流分量，然后再进行频域变换处理。加窗函数是提高频率分析质量的一个重要措施，选用合理的窗函数能够抑制假频率和提高信噪比。加窗的目的一般有两个：首先提高离散频谱分析的幅值精度，第二是抑制假频率和提高信噪比，假频率出现的原因是常用窗口函数的幅值存在旁瓣，无限域上的高斯窗和傅里叶核窗函数没有旁瓣，而实际的操作只能在有限的时域上进行，所以有限时域的窗口函数总存在旁瓣，但如果能够选择合适的窗函数可以将能量的绝大部分集中到主瓣内，基本避免假频的出现[8-10]。常用的改善频谱的窗口函数有Hamming窗与Hanning窗。

Hanning窗又称为升余弦窗，Hanning窗可以看作是3个矩形时间窗的频谱之和，加权系数能够使旁瓣更小，其表达式如下：

(12)

Hamming窗是一种改进的余弦窗，它与Hanning窗基本一样，二者加权系数稍微有些不同，Hamming窗的表式为：

(13)

取α=0.5，长度为1 000的Hanning窗口进行仿真，时域图与频域如图7所示。

图7(b)中Hanning窗的旁瓣衰减速率比较快，能量泄露比较少。加Hanning窗可以将谐波信号加矩形窗离散频谱分析的幅值最大误差从36.3%降低到15.1%。在光谱分辨干涉的非模糊距离内，分别利用矩形窗与Hanning窗对经过傅里叶变换的时域波形滤波，然后计算被测距离，仿真测量误差如图8所示，从图中可以看出利用Hanning窗进行滤波后，距离计算精度有所提高。

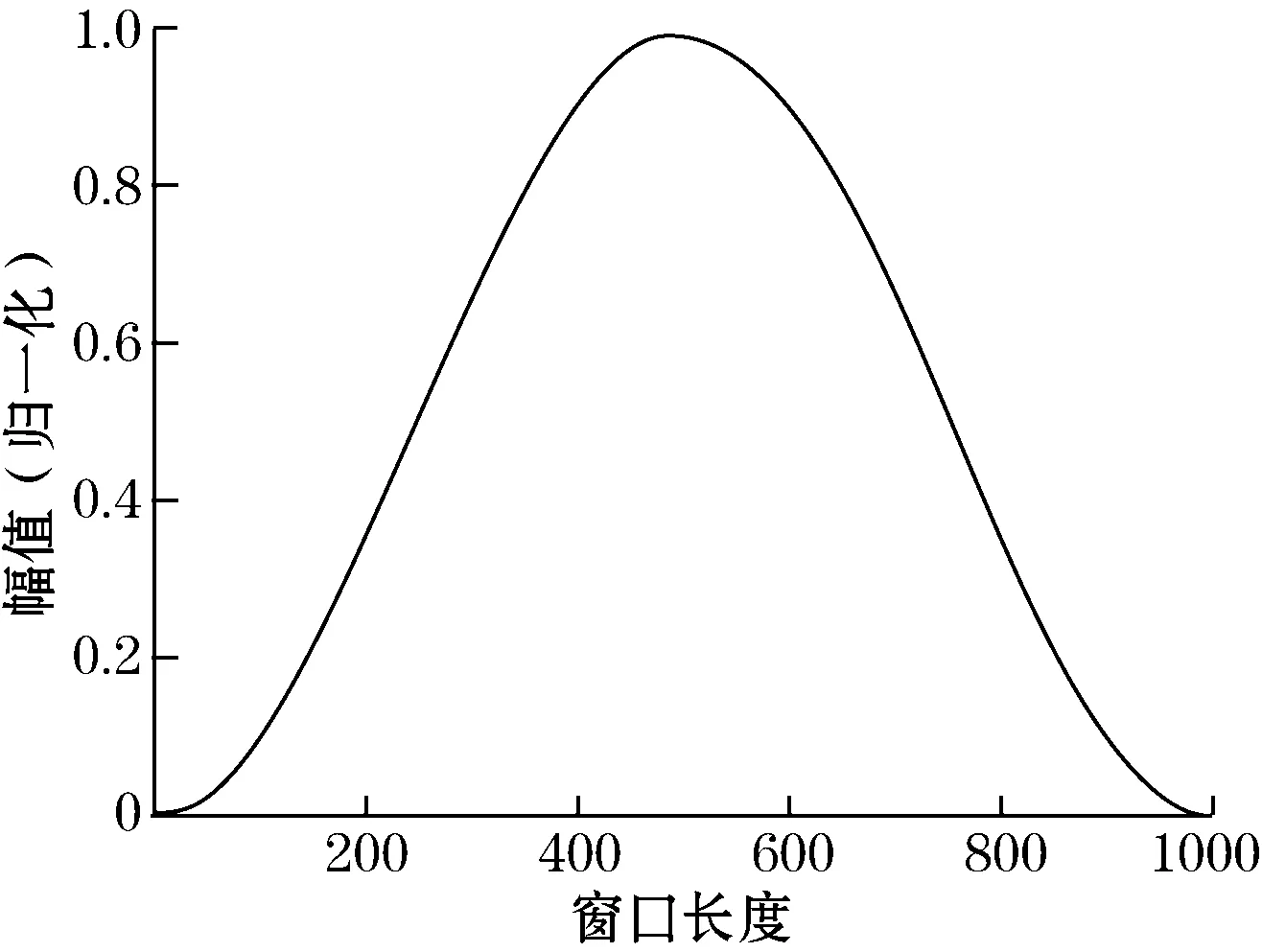
(a) Hanning窗时域图

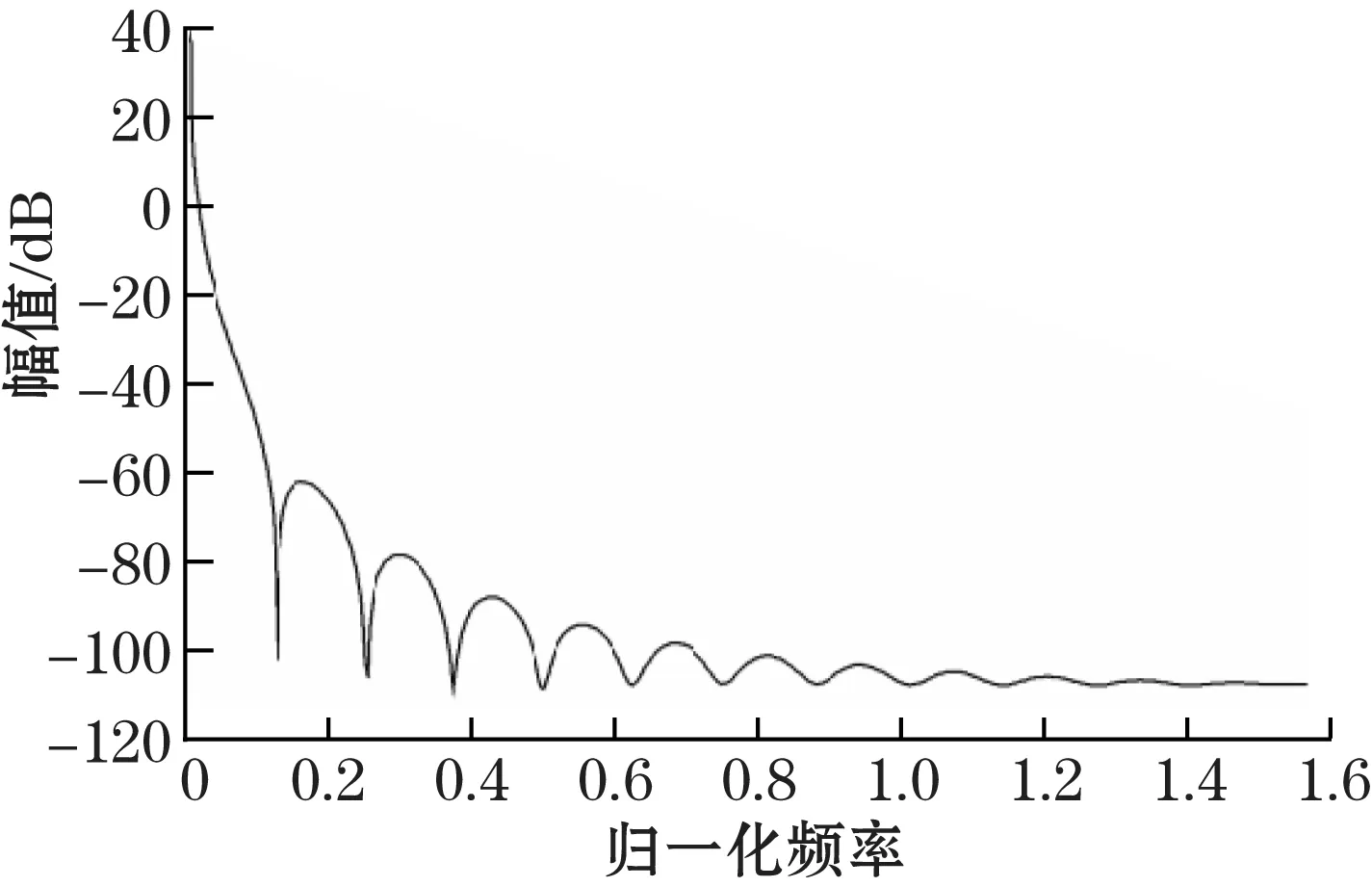
(b) Hanning 频域图图7 Hanning窗口时域图和频域图

仿真结果表明，使用Hanning窗或者Hamming窗滤波均可以提高计算精度，二者的提高效果也一致。因此，可以利用Hanning窗或者Hamming窗对光谱分辨干涉信号进行时域滤波，提高数据处理精度，改善测距误差。

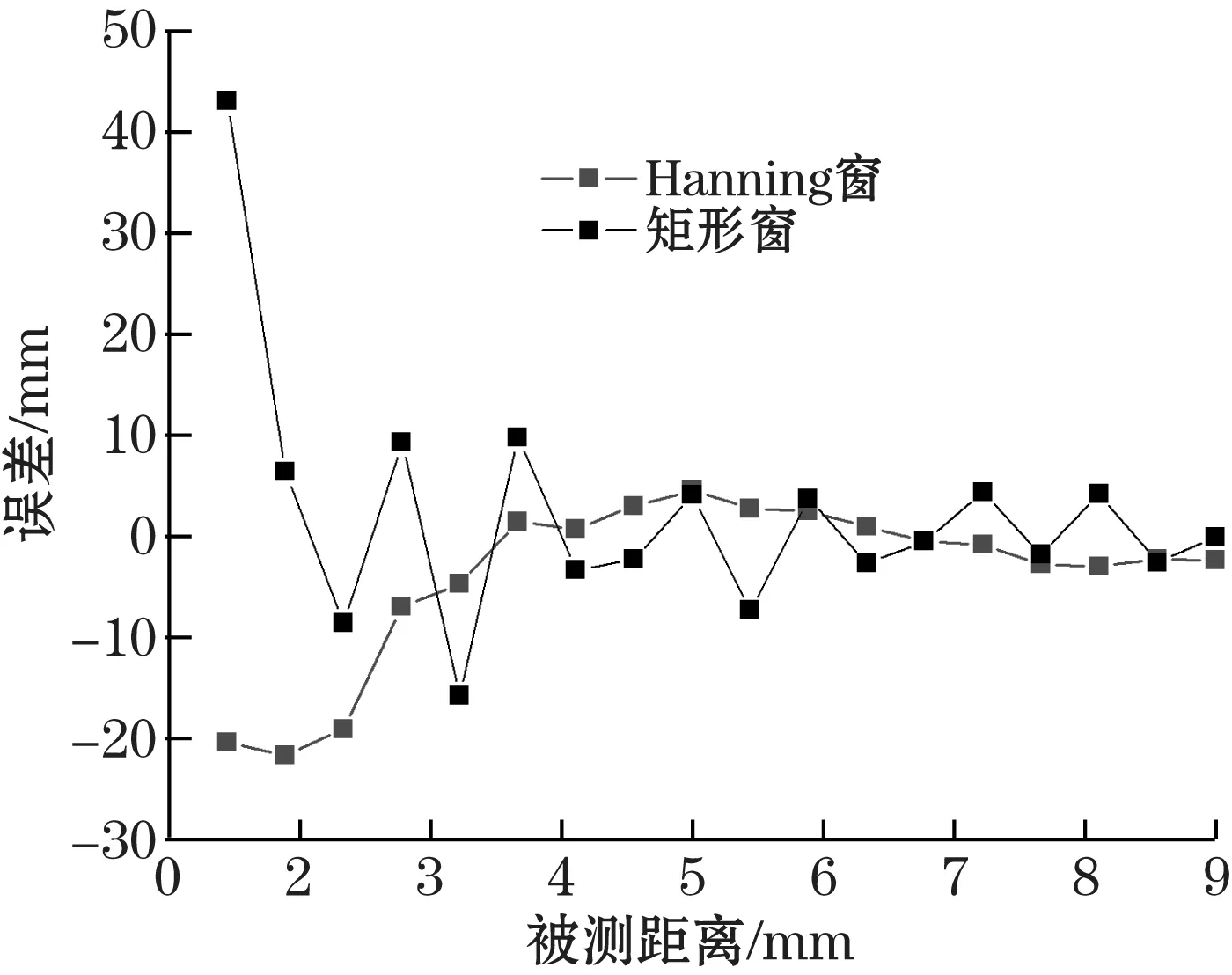
图8 Hanning窗与矩形窗滤波仿真测量误差

3 测量实验

搭建飞秒激光测距实验，如图9所示，实验中加入XL-80型干涉仪进行光路调整与测量数据对比。

图9 光谱分辨干涉测距实验图

调整两个臂长相等后，以50 μm为步进值测量20组数据并记录。对干涉信号进行处理求解被测距离，图10为测量值与干涉仪测量值比对偏差。

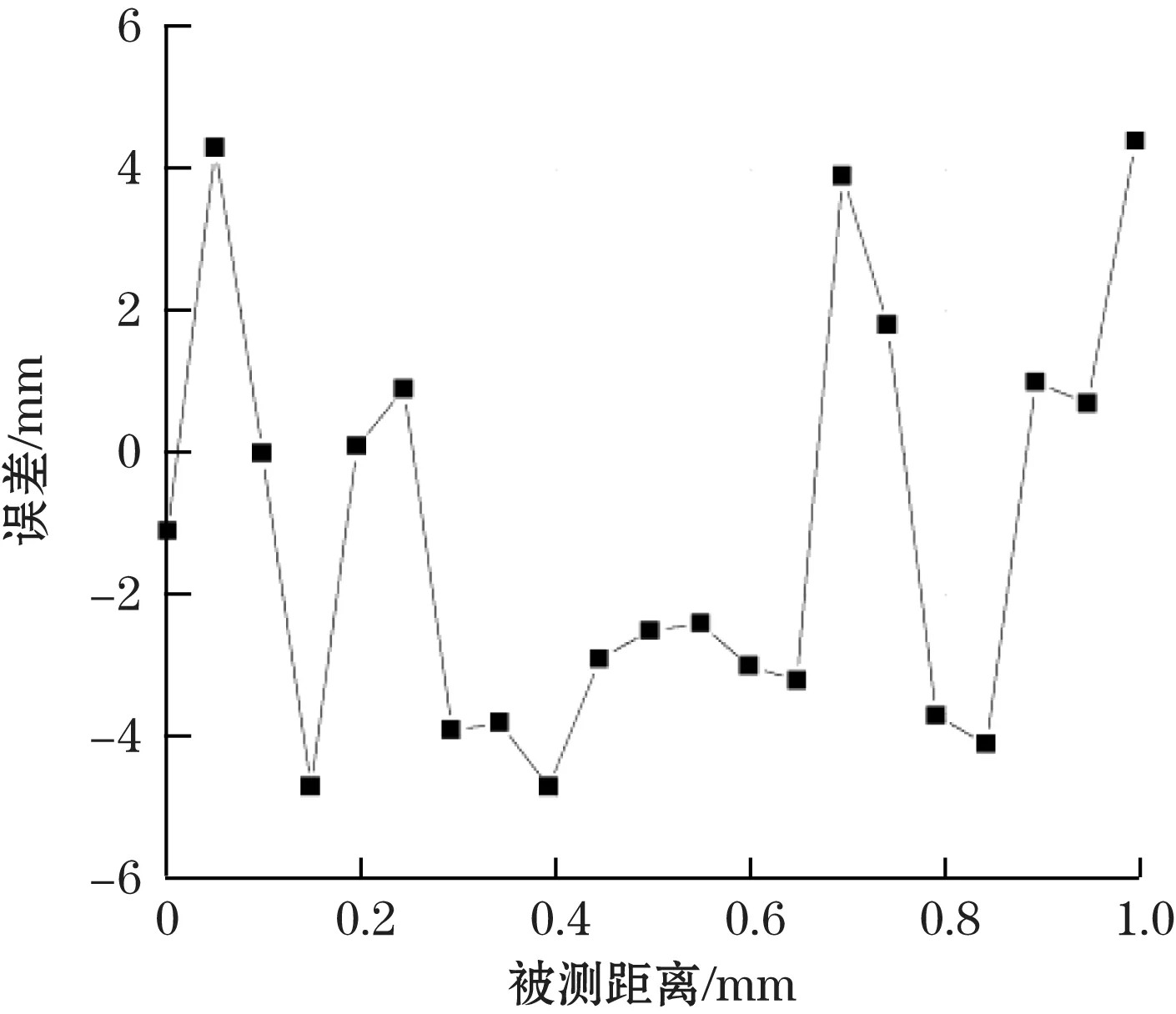
图10 测量值比对偏差

4 结论

本文针对飞秒激光测距频谱干涉条纹信号，分析了被测距离精度对于相位信息采集与处理要求，根据飞秒激光测距信号干涉谱的数学关系，采用傅里叶变换和坐标旋转数字计算法进行光谱分辨干涉信号处理，反复利用傅里叶变换与反变换并在中间过程加入滤波，最后仿真计算出频率对应的相位值进而获得被测距离值。实验测试结果表明，该方法能够有效提高飞秒激光测距信号处理精度。

[1] HYUN, KIM Y J. KIM Y, et al. Absolute distance measurement using the frequency comb of a femtosecond laser. Manufacturing Technology, 2010，59: 555-558.

[2] 华卿. 基于全路径大气折射率补偿的多波长测距原理与实验研究：[学位论文].北京： 中国科学院大学，2013.

[3] 华卿, 周维虎, 徐艳. 飞秒激光频率梳绝对测距技术综述. 计测技术,2011, 31(1): 1-5.

[4] 许艳. 基于飞秒激光频率梳的绝对距离测量技术研究:[学位论文].武汉：华中科技大学,2012.

[5] 武腾飞, 梁志国, 严家骅，等. 飞秒光学频率梳测距技术的研究进展. 计测技术, 2011, 31(5): 162-167.

[6] DONG W, MASATO A. Comparison of length measuremests provided by a femtosecond optical frequency comb. Opt. Exp., 2014, 22(6): 7040-7045.

[7] 安慰宁, 张福民, 吴翰钟，等. 一种基于飞秒光频梳频域干涉的绝对测距方法. 仪器仪表学报, 2014, 35(11): 2458-2465.

[8] 王辉俊，刘永涛，尤文强，等. 一种基于改进差值算法的手持激光测距仪. 仪表技术与传感器，2013(1):97-99.

[9] LEE J, LEE K, LEE S, et al. High precision laser ranging by time of flight measurement of femtosecond pulses. MeasSciTechnol, 2012,23(8):1-8.

[10] 徐艳, 周维虎, 刘德明,等. 基于飞秒激光器光学频率梳的绝对距离测量. 光电工程, 2011, 38(8): 79-81.

Phase Ranging Signal Analysis and Processing of Femtosecond Laser Frequency Domain Interference

LIU Jiao-yue1，3, YANG Ju-qing2,3

(1. Henan Polytechnical Institute，Nanyang 473009，China;2. Collage of Applied Science, Beijing University of Technology, Beijing 100124, China.3. Academy of Opto-Electronics, Chinese Academy of Science, Beijing 100094,China)

In view of the femtosecond laser ranging spectrum interference fringe signals, requirements for phase information acquisition and processing to distance measurement precision were analyzed, data processing of interference spectral resolution distance measurement were introduced in details. According to the mathematical relationship of ranging signal interference spectrum, the measured distance formula was deduced. Fourier transform method was used to realize the spectral resolution of interference signal processing, after many links such as time-domain signal’s Fourier transform, signal’s phase solution package, add window function time-domain signal’s filtering, each frequency’s phase value of interference fringe signals was processed and transformed respectively. After system simulation, the biggest error of the amplitude of discrete spectrum analysis reduced from 36.3% to 15.1%.Through the comparison experiment, the method can realize femtosecond laser ranging signal processing effectively.

femtosecond laser ranging; spectrally resolved interferometry; phase signal process.

国家自然科学基金资助项目(No.61377103)；北京工业大学研究生科技基金项目(No.ykj-2014-11443)

2015-06-06

TH741；TN249

A

1002-1841(2015)09-0099-04

刘娇月(1974—)，副教授，硕士，主要从事精密仪器、机电一体化技术及应用等。E-mail:15838706952@139.com 杨聚庆(1972—)，副教授，在读博士，主要研究方向为光电检测与控制及激光跟踪测量技术等。E-mail:nyyjq@139.com